Trigonometri
| Geometri |
|---|
 |
| Geometriciler |
Trigonometri (Yunanca trigōnon "üçgen" + metron "ölçmek"), üçgenlerin açıları ile kenarları arasındaki bağıntıları konu edinen matematik dalı. Trigonometri, sinüs ve kosinüs gibi trigonometrik işlevlerin (fonksiyon) üzerine kurulmuştur ve günümüzde fizik ve mühendislik alanlarında sıkça kullanılmaktadır.
Tarihçe[değiştir | kaynağı değiştir]
Matematiğin doğrudan doğruya astronomiden çıkmış bir kolu olan trigonometrinin bazı ögeleri, daha Babilliler ve Eski Mısırlılar döneminde biliniyor, Sümerli astronomlar ilk kez bir çemberi 360 eşit parçaya bölerek açı ölçümünü yaptılar. Eski Yunanlar Menelaos’un küresel geometrisi aracılığıyla, bir daire içine çizilebilen dörtgenden yola çıkarak daire yaylarının kirişlerinin değerlerini veren çizgiler oluşturuyorlardı. Daha sonra Araplar, yay kirişlerinin yerine sinüsleri koyup; tanjant, kotanjant, sekant, kosekant kavramlarını geliştirdiler.[kaynak belirtilmeli].İlk kez Akdeniz'in çevresi trigonometre ile Abbasiler döneminde ölçülmüştür.[kaynak belirtilmeli]
Batıda Nasîrüddin Tûsî’den büyük ölçüde yararlanan Regiomontanus’un üçgen üstüne adlı eseriyle gerçek trigonometri doğmuş oldu. François Viète ve Simon Stevin, hesaplarda ondalık sayılardan yararlandılar. John Napier logaritmayı işe kattı. Isaac Newton ve öğrencileri trigonometri işlevlerinin ve logaritmalarının hesabına tam serileri uyguladılar. Daha sonra da Leonhard Euler, birim olarak trigonometrik cetvelin yarıçapını alarak, modern trigonometrinin temellerini attı.[kaynak belirtilmeli].
Genel bakış[değiştir | kaynağı değiştir]
Trigonometrik işlevler[değiştir | kaynağı değiştir]

Trigonometrik işlevler bir dik üçgen ya da birim çember üzerinden tanımlanır. Temel olarak üç tane trigonometrik işlev ve bunların çarpma işlemine göre terslerinden oluşan üç tane daha işlev vardır. Yandaki ABC üçgeninde
- Sinüs işlevi (sin), karşı kenarın hipotenüse oranıdır.
- Kosinüs işlevi (cos), komşu kenarın hipotenüse oranıdır.
- Tanjant işlevi (tan), karşı kenarın komşu kenarı oranıdır.
Bir de bu işlevlerin çarpmaya göre tersi vardır. kosekant, sekant ve kotanjant:
Bu işlevler geometrinin dolayısıyla fiziğin ve mühendisliğin pek çok alanında kullanılır. Sinüs ve kosinüs teoremleri bir üçgenin açıları ve kenarlarını hesaplamakta kullanılır ki herhangi bir çokgen üçgenlerin birleşimi olduğundan çokgenleri incelemede de yararlıdır.
Birim çember ve esas ölçü[değiştir | kaynağı değiştir]
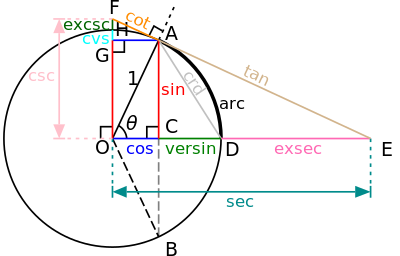
Yukarıda dik üçgen üzerinden yapılan tanım sadece 0-90 derece aralığını kapsar (0-π/2 radyan).
90-360 derece arasındaki açıların trigonometrik değerleri birim çember üzerinden hesaplanır. 360 dereceden büyük açılar 360 üzerinden devrettirilerek 0-360 arasındaki esas ölçüsü bulunur.
- 0° ≤x <360° ve k bir tam sayı olmak üzere ölçüsü (x + 360k) olan açıların esas ölçüsü x derecedir.
- 0 ≤ x< 2π ve k bir tam sayı olmak üzere, ölçüsü (x + 2πk) olan açıların esas ölçüsü x radyandır.
Merkezi orijin ve yarıçapı 1 birim olan çembere birim çember veya trigonometrik çember denir. Birim çemberin denklemi x2+y2=1 şeklindedir.
Sarma işlevi[değiştir | kaynağı değiştir]
Gerçel sayılar kümesinden birim çember üzerindeki noktalara tanımlanan işleve sarma işlevi denir.
Sarma işlevini s ile, birim çemberi de C ile gösterirsek işlev
şeklinde yazılabilir ve oldugunda olur. Başka bir deyişle, sarma işlevi, gerçel sayılar üzerinde dönemi (periyodu) olan bir işlevdir.
İşlevler arasındaki ilişkiler[değiştir | kaynağı değiştir]
Yukarıdaki tanımlardan görülebileceği gibi, bu işlevler arasında
ilişkileri vardır.
Sık kullanılan açıların trigonometrik oranları[değiştir | kaynağı değiştir]
| [1] | [2] | |||||||
| [3] | [4] | [5] | ||||||
| [6] | [7] | |||||||
| [8] | [9] | [10] |
Gerçek veya karmaşık değişkenlerin trigonometrik fonksiyonları[değiştir | kaynağı değiştir]
Trigonometrik fonksiyon grafikleri[değiştir | kaynağı değiştir]
6 ana trigonometrik fonksiyonun özelliklerini özetleyen diyagramlar:[11][12]
| Fonksiyon | Periyot | Alan | Aralık | Diyagram |
|---|---|---|---|---|
| sinüs | 
| |||
| cosinüs | 
| |||
| tanjant | 
| |||
| sekant | 
| |||
| cosekant | 
| |||
| cotanjant | 
|
Ters trigonometrik fonksiyonlar[değiştir | kaynağı değiştir]
6 ana trigonometrik fonksiyon periyodik olduğu için birebir değillerdir yani ters çevrilemezler, ancak trigonometrik bir fonksiyonun alanını kısıtlayarak ters çevrilebilirler.[13]:48ff
| Fonksiyon | Genel gösterim | İfade | x değer aralığı | Asıl değer aralığı (radyan) |
Asıl değer aralığı (derece) |
|---|---|---|---|---|---|
| arcsinüs | y = arcsin x | x = sin y | −1 ≤ x ≤ 1 | −π/2 ≤ y ≤ π/2 | −90° ≤ y ≤ 90° |
| arckosinüs | y = arccos x | x = cos y | −1 ≤ x ≤ 1 | 0 ≤ y ≤ π | 0° ≤ y ≤ 180° |
| arctanjant | y = arctan x | x = tan y | tüm reel sayılar | −π/2 < y < π/2 | −90° < y < 90° |
| arckotanjant | y = arccot x | x = cot y | tüm reel sayılar | 0 < y < π | 0° < y < 180° |
| arcsekant | y = arcsec x | x = sec y | x ≤ −1 or 1 ≤ x | 0 ≤ y < π/2 or π/2 < y ≤ π | 0° ≤ y < 90° or 90° < y ≤ 180° |
| arckosekant | y = arccsc x | x = csc y | x ≤ −1 or 1 ≤ x | −π/2 ≤ y < 0 or 0 < y ≤ π/2 | -90° ≤ y < 0° or 0° < y ≤ 90° |
Kullanım alanları[değiştir | kaynağı değiştir]

Trigonometri birçok fen biliminde, matematiğin diğer alanlarında ve çeşitli sanatlarda yaygın bir biçimde kullanılmaktadır. Trigonometriyi kullanan bazı dallar şunlardır:
jeofizik, kristalografi, ekonomi (özellikle de finansal pazarların analizinde), elektrik mühendisliği, inşaat mühendisliği, elektronik, jeodezi, makine mühendisliği, meteoroloji, müzik kuramı, sayı kuramı (ve dolayısıyla kriptografi), oşinografi (okyanus bilimi), farmakoloji (eczacılık), optik, fonetik, olasılık kuramı, psikoloji, sismoloji...
Trigonometri yukarıda örneklendiği gibi birçok farklı alana farklı katkılarda bulunmuştur. Örneğin Pisagor kuramının isim babası Pisagor matematiksel müzik kuramına ilk katkıda bulunan isimlerdendir. Oşinografide bazı dalgaların sinüs dalgalarına benzerliği ilgili incelemelerde trigonometrinin kullanımına olanak tanımıştır. Bunun dışında Fourier serileri sayesinde trigonometrik işlevler farklı fonksiyonları temsil etmekte kullanılırlar ve bu sayede trigonometri birçok yararlanılan dallarda kullanım olanağı bulmuştur.
Özdeşlikler[değiştir | kaynağı değiştir]
Üçgen özdeşlikleri[değiştir | kaynağı değiştir]
Sinüs teoremi[değiştir | kaynağı değiştir]
Kosinüs teoremi[değiştir | kaynağı değiştir]
Tanjant teoremi[değiştir | kaynağı değiştir]
Trigonometrik özdeşlikler[değiştir | kaynağı değiştir]
Euler bağıntısı[değiştir | kaynağı değiştir]
Bu bağıntıyla iki matematiksel ifade olan i ve birbirine bağlanmış olur.
de Moivre formülü[değiştir | kaynağı değiştir]
Diğer özdeşlikler[değiştir | kaynağı değiştir]
Toplam fark formülleri[değiştir | kaynağı değiştir]
Trigonometrik değerleri bilinen iki açının toplamının veya farkının trigonometrik değerlerini hesaplamak için kullanılan formüllerdir.
sin(α+β) = sin α.cos β + cos α.sin β
sin(α-β) = sin α.cos β - cos α.sin β
cos(α+β) = cos α.cos β - sin α.sin β
cos(α-β) = cos α.cos β + sin α.sin β
tan(α+β) = (tan α + tan β) / (1 - tan α . tan β)
tan(α-β) = (tan α - tan β) / (1 + tan α . tan β)
cot(α+β) = (cot α . cot β - 1) / (cot α + cot β)
cot(α-β) = (cot α . cot β + 1) / (cot β - cot α)
Yarım açı formülleri[değiştir | kaynağı değiştir]
Yarım açı formülleri ya da iki kat açı formülleri, trigonometrik değerleri bilinen bir açının iki katının veya yarısının trigonometrik değerlerini hesaplamak için kullanılan formüllerdir.
sin2α = 2sin α.cos α
cos2α = cos2 α - sin2 α
cos2α = 2cos2 α - 1
cos2α = 1- 2sin2 α
tan2α = 2tan α / 1-tan2 α
tan2α = 2 / cot α - tan α
cot2α = cot2 α - 1 / 2cot α
Dönüşüm formülleri[değiştir | kaynağı değiştir]
Dönüşüm formülleri, toplam durumundaki iki trigonometrik ifadeyi çarpım haline getirmeye yarar. Bu işlemin amacı bazı özel durumlarda işlem kolaylığı sağlamaktır.
Ayrıca bakınız[değiştir | kaynağı değiştir]
Notlar[değiştir | kaynağı değiştir]
- ^ "Arşivlenmiş kopya". 11 Temmuz 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Kasım 2020.
- ^ "Arşivlenmiş kopya". 27 Şubat 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Kasım 2020.
- ^ "Arşivlenmiş kopya". 20 Aralık 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Kasım 2020.
- ^ "Arşivlenmiş kopya". 27 Şubat 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Kasım 2020.
- ^ "Arşivlenmiş kopya". 27 Şubat 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Kasım 2020.
- ^ "Arşivlenmiş kopya". 27 Şubat 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Kasım 2020.
- ^ "Arşivlenmiş kopya". 27 Şubat 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Kasım 2020.
- ^ "Arşivlenmiş kopya". 27 Şubat 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Kasım 2020.
- ^ "Arşivlenmiş kopya". 27 Şubat 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Kasım 2020.
- ^ "Arşivlenmiş kopya". 27 Şubat 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Kasım 2020.
- ^ Mary P Attenborough (30 Haziran 2003). Mathematics for Electrical Engineering and Computing. Elsevier. s. 418. ISBN 978-0-08-047340-6. 12 Mart 2022 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Mart 2022.
- ^ Ron Larson; Bruce H. Edwards (10 Kasım 2008). Calculus of a Single Variable. Cengage Learning. s. 21. ISBN 978-0-547-20998-2. 22 Mayıs 2022 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Mart 2022.
- ^ Elizabeth G. Bremigan; Ralph J. Bremigan; John D. Lorch (2011). Mathematics for Secondary School Teachers. MAA. ISBN 978-0-88385-773-1. 5 Mayıs 2022 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Mart 2022.










































![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)


![{\displaystyle (-\infty ,-1]\cup [1,\infty )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e3448e2de68557e598967fb8b1f8900260c4a64)











