Dik
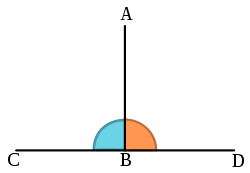
Geometride, iki doğru veya iki düzlem (veya bir doğru ve bir düzlem) kesiştiklerinde oluşturdukları komşu açılar birbirine eşitse dik olarak kabul edilir.
Bir doğru sonsuz uzunluktadır ve yukarıdaki örnekte AB ve CD iki sonsuz uzunluktaki doğruya ait doğru parçalarıdır. Sonuçta, AB doğru parçası, CD ile dik olmak için onu kesmek zordunda değildir, çünkü iki doğru parçası sonsuza kadar uzatıldığında, aralarındaki açılar yine benzer olacaktır.
Eğer gösterildiği gibi bir doğru, bir diğerine dikse kesişimlerinde oluştan tüm açılar doğru açı olarak adlandırılır (doğru açı π/2 radyan ya da 90°'dir). Tersinden bakıldığında, aralarında doğru açı oluşturan doğrular birbirine diktir.
Koordinat düzleminde, dik doğrular birbirine zıt karşılık eğimlere sahiptir. Yatay bir doğrunun eğimi sıfırken dikey bir doğrunun eğimi tanımsız ya da bazen ±sonsuz olarak tanımlanır. Birbirine dik iki doğru ABCD şeklinde gösterilir.
Dik bir doğru çizmek[değiştir | kaynağı değiştir]
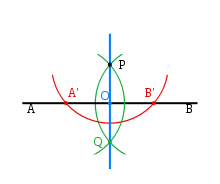
P noktasından AB doğrusuna pergel ve cetvel kullanarak dik çizmek için, şu adımlar uygulanmalıdır:
- 1 (kırmızı): AB doğrusu üzerinde P'den eşit uzaklıktaki A' ve B' noktalarını belirlemek için P merkezli bir çember çizin.
- 2 (yeşil): İkisi de P noktasından geçen A' ve B' merkezli iki çember daha çizin. Bu iki çemberin diğer kesiştiği nokta Q olsun.
- 3 (mavi): P ve Q noktalarını birleştiren dik PQ doğrusu çizin.
PQ'nun AB'ye dik olduğunu kanıtlamak için QPA' ve QPB' üçgenlerinde KKK Benzerlik teoremi kullanılır ve OPA' ile OPB' açılarının eşit olduğu görülür. Daha sonra OPA' ve OPB' üçgenlerinde KAK Benzerlik teoremi kullanılarak POA ve POB açılarının eşit olduğu anlaşılır.
Paralel doğrularla ilişkisi[değiştir | kaynağı değiştir]

Eğer iki doğru (a ve b) birden üçüncü bir doğruya (c) dikse, üçüncü doğru üzerinde oluşan tüm açılar doğru açıdır. Öklid geometrisinde üçüncü bir doğruya dik olan iki açı, birbirine paraleldir. Tersten bakıldığına, bir doğru diğerine dikse, ikinci doğruya paralel olan bütün doğrulara da diktir.
Sağdaki şekilde, turuncuyla işaretlenmiş tüm açılar birbirine benzerdir ve yeşille işaretlenmiş şekiller de kendi içinde benzerdir, çünkü ters açı oluştururlar. Eğer a ve b birbirine paralelse, aşağıdakilerden herhangi birinin doğru olduğu durumda hepsi doğru olacaktır:
- Diyagramdaki açılardan biri doğru açıdır.
- Turuncu açılardan birisi yeşil açılardan birine eşittir.
- 'c' doğrusu 'a' doğrusuna diktir.
- 'c' doğrusu 'b' doğrusuna diktir.
Diklik sembolü[değiştir | kaynağı değiştir]
Diklik sembolü 'dir. Örneğin, AB doğrusunun CD doğrusuna dik olduğunu gösterir.
Unicode karakter setinde, diklik sembolü U+27C2 kod numarasına sahiptir ve Çeşitli Matematik Sembolleri-A kümesindedir. Up tack sembolüne (U+22A5) benzer.
Fonksiyonların grafiği[değiştir | kaynağı değiştir]
2-boyutlu düzlemde, eğimlerinin çarpımı -1 olan doğrular doğru açı oluşturur. Daha açıkça ifade etmek gerekirse, y1 = a1x + b1 ve y2 = a2x + b2 şeklinde iki doğrusal fonksiyon tanımladığımızda, fonksiyonlar grafiklerinin birbirine dik olması ve kesiştikleri noktada dört doğru açı oluşturması için a1a2 = −1 doğru olmalıdır. Fakat bu yöntem doğruların eğiminin sıfır ya da sonsuz olduğu durumlarda (aksislere paralel olma durumu) kullanılamaz.
Ayrıca bakınız[değiştir | kaynağı değiştir]
- Diklik
- Dik bileşen (vektörler için)
- Yüzey normali
- Paralel (geometri)
Dış bağlantılar[değiştir | kaynağı değiştir]
- Tanım: dik25 Eylül 2018 tarihinde Wayback Machine sitesinde arşivlendi. etkileşimli animasyonla birlikte (İngilizce)
- Pergel ve cetvel kullanarak bir doğru parçasını ikiye bölen dikme çizmek16 Ocak 2017 tarihinde Wayback Machine sitesinde arşivlendi. Animasyonlu gösterim (İngilizce)
- Pergel ve cetvel kullanarak bir doğru parçasının başlangıç noktasından geçen dik çizmek 1 Ocak 2012 tarihinde Wayback Machine sitesinde arşivlendi. Animasyonlu gösterim (İngilizce)


