Çevrel çember

Çevrel çember, geometride, bir çokgenin tüm köşelerinden geçen çember. Bu çemberin merkezi çevrel özek (çevrel çemberin merkezi) olarak isimlendirilir.[1]
Çevrel çemberi olan çokgenler, devirsel çokgen olarak isimlendirilir. Bütün düzgün basit çokgenler, üçgenler ve dörtgenler bu özelliği gösterir.
Üçgende çevrel çember[değiştir | kaynağı değiştir]

Her üçgen devirseldir; bir başka ifadeyle tüm üçgenlerin bir çevrel çemberi bulunur.[nb 1]
Bir üçgenin çevrel çemberinin merkezi herhangi iki kenar ortadikmesinin kesişim noktası alınarak bulunabilir. (Ortadikme üçgenin bir kenarıyla doksan derecelik açı yapan ve aynı zamanda bu kenarı orta noktasında kesen doğrudur.) Çünkü çevrel çemberin merkezi, üçgendeki herhangi iki köşe çiftine eşit uzaklıktadır ve ortadikme üzerindeki tüm noktalar da üçgenin iki köşesine aynı mesafede bulunma şartını sağlar.
Çevrel çember merkezinin konumu üçgenin türüne göre değişir. Çevrel çemberin merkezi:
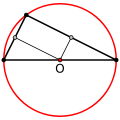
- Ancak ve ancak üçgen dar açılı (tüm açıları doksan dereceden küçük) ise, üçgenin içindedir.
- Ancak ve ancak üçgen geniş açılı ise (doksan dereceden büyük bir açıya sahip), üçgenin dışındadır.
- Ancak ve ancak üçgen dik açılı ise, hipotenüsün orta noktasındadır. Bu durum Thales teoreminin bir türüdür.
-
Dar açılı bir üçgenin çevrel çemberinin merkezi, üçgenin içinde yer alır
-
Dik açılı bir üçgenin çevrel çemberinin merkezi, üçgen hipotenüsünün orta noktasıdır
-
Geniş açılı bir üçgenin çevrel çemberinin merkezi, üçgenin dışında yer alır
Çevrel çemberin çapı, üçgenin herhangi bir kenar uzunluğunun, kenarı gören açının sinüsüne bölünmesiyle hesaplanabilir. (Sinüs teoreminin bir sonucu olarak, hangi kenar seçilirse seçilsin sonuç aynı olacaktır.) Üçgenin dokuz nokta çemberinin çapı, çevrel çemberin çapının yarısına eşittir. ΔABC üçgenin çevrel çemberinin çapı:
burada R çap uzunluğunu, a, b, c üçgenin kenar uzunluklarını ve s = (a + b + c)/2 yarı çevre uzunluğunu simgeler. Yukarıda ikinci paydadaki köklü ifade, Heron formülüne göre, üçgenin alan ifadesidir.[1] Çemberin çapı için yazılabilecek trigonometrik ifadelerden biri[2]
Verilen herhangi bir üçgende, çevrel çemberin merkezi daima sentroid (kenarotayların kesişim noktası) ve yüksekliklerin kesişim noktası doğrusaldır. Bu noktaların tümünden geçen doğru Euler doğrusu olarak bilinir.
Çevrel çember merkezinin izogonal eşleniği yüksekliklerin kesişim noktasıdır.
Üç doğrusal noktanın çevrel çemberi olan, bu noktalardan geçen doğru sonsuz yarıçaplı çember olarak anılır. Neredeyse doğrusal olan noktaların çevrel çember hesaplamalarında genellikle sayısal kararsızlık görülür.
Üçgen çevrel çemberlerinin, bir noktalar kümesinin Delaunay üçgenlemesi ile yakın ilişkisi vardır.
Çevrel çember denklemleri[değiştir | kaynağı değiştir]
Öklid düzleminde, bir çevrel çember denklemi ait olduğu üçgeninin köşelerinin Kartezyen koordinatlarından elde edilebilir. Buna göre
A, B ve C noktalarının koordinatları olarak alınsın. Burada çevrel çember, Kartezyen düzlemde geometrik yeri aşağıdaki denklemleri sağlayan v = (vx,vy) noktalarıdır.
Denklemlerle A, B, C ve v'nin, çemberin merkezi u' dan eşit r2 uzaklıkta olması sağlanır. Kutuplanma özdeşliği kullanılarak denklemler
matrisine indirgenebilir. Böylece çevrel çember, matris determinantının sıfırlarının geometrik yeriyle ifade edilir:
Kofaktör açılımı ile,
a|v|2 − 2Sv − b = 0 elde edilir ve üç noktanın doğrusal olmadığı varsayımıyla (aksi durumda çevrel çember S'nin sonsuzda olduğu bir doğru halini alır), |v − S/a|2 = b/a + |S|2/a2, S/a çevrel çember merkezi ve √ (b/a + |S|2/a2) yarıçapı hesaplanır. Benzer yaklaşımla bir dörtyüzlünün çevrel küre denklemi de bulunabilir.
Çevrel çemberin trilineer koordinatlarla ifade edilmiş bir denklemi x : y : z is a/x + b/y + c/z = 0 ve barisentrik koordinatlarla ifade edilmiş bir denklemi x : y : z is a2/x + b2/y + c2/z = 0 şeklindedir.
Çevrel çemberin izogonal işleniği sonsuzdaki doğrudur; trilineer koordinatlarla ax + by + cz = 0 ve barisentrik koordinatlarla x + y + z = 0 olarak gösterilebilir.
Bunun yanında, d boyuttaki bir üçgenin çevrel çemberi, genelleştirilmiş bir yöntemle bulunabilir. A, B ve C üçgenin köşelerini ifade eden d-boyutlu noktalar olsun. İşlemler C orijine taşınarak başlar:
Çevrel çemberin yarıçapı, r,
burada θ a ve b arasındaki iç açıdır. Çevrel çemberin merkezi, p0,
şeklinde ifade edilebilir.
Çevrel çember merkezinin koordinatları[değiştir | kaynağı değiştir]
Kartezyen koordinatlar[değiştir | kaynağı değiştir]
Çevrel çember merkezinin Kartezyen koordinatları
ve
Denklemler, genelleştirilmiş durum kaybolmadan, A köşesi Kartezyen koordinat sisteminin orijinine taşınarak yazılabilir; yani alınır. Bu durumda köşe koordinatları B' = B − A and C' = C − A A''dan köşelere çizilmiş vektörleri gösteren. Bu üçgensel çeviri tüm üçgenler için geçerlidir ve A'B'C' üçgeninin çevrel çemberinin merkez koordinatları şöyledir:
burada
Kenar uzunluklarının fonksiyonu olarak barisentrik koordinatlar[değiştir | kaynağı değiştir]
Çevrel çemberin merkezi barisentrik koordinatlarla
ifade edilir. Burada a, b, c üçgenin kenar uzunluklarını (sırasıyla BC, CA, AB) göstermektedir.
Vektörel ve skaler çarpımla barisentrik koordinatlar[değiştir | kaynağı değiştir]
Öklid uzayında alınan, doğrusal olmayan herhangi P1, P2 ve P3 noktasından geçen bir çember bulunur. Kartezyen koordinatlar kullanılarak bu noktalar vektör olarak yazılırsa, vektörel çarpım ve skaler çarpımla çevrel çember yarıçapı ile merkezi hesaplanabilir.
olsun. Bu noktalardan geçecek çemberin yarıçapı şöyle ifade edilir:
Çemberin merkezi ise lineer kombinasyonla:
şeklinde gösterilir. Burada
Parametrik denklemler[değiştir | kaynağı değiştir]
Çevrel çemberin bulunduğu düzeleme dik bir birim vektör şöyle yazılabilir:
Böylece çevrel çember yarıçapı, r, merkezi, Pc, çember üzerindeki bir nokta, P0 ve çemberin bulunduğu yüzeye ait birim normal, , olmak üzere, P0 noktasından başlayarak 'ye pozitif yönelen (sağ el yönünde) çemberin bir parametrik ifadesi:
Çemberin kenarlarla yaptığı açılar[değiştir | kaynağı değiştir]
 |
 |
Çevrel çemberin üçgenin kenarlarıyla yaptığı açılar, bu kenarların üçüncü kenarla oluşturduğu üçgen iç açılarına eşittir.
Çevrel çemberin diğer özellikleri[değiştir | kaynağı değiştir]
Çevrel çemberin yarıçapı, iç teğet çemberin yarıçapının iki katından küçük değildir. (Euler'in üçgen eşitsizliği)[4]
Çevrel çemberin merkezi ile iç teğet çemberin merkezi arasındaki uzaklık 'dır; r iç teğet çember yarıçapını ve R çevrel çember yarıçapını simgelemektedir.[4]
a, b ve c kenarlarına sahip üçgenin çevrel çemberinin yarıçapının, iç teğet çemberinin yarıçapıyla çarpımı[5] şeklinde olacaktır.
Notlar[değiştir | kaynağı değiştir]
- ^ Bu durum Kartezyen koordinat sisteminde alınacak r yarıçaplı ve merkez koordinatları a, b olan bir genel çember denklemi üzerinden ispatlanabilir:
Kaynakça[değiştir | kaynağı değiştir]
- ^ "TDK Matematik Terimleri Sözlüğü". TDK. Erişim tarihi: 9 Ağustos 2011.[ölü/kırık bağlantı]
- ^ Dörrie, Heinrich, 100 Great Problems of Elementary Mathematics, Dover, 1965. :s.379
- ^ "Wolfram barisentrik koordinatlar (İngilizce)". 20 Temmuz 2017 tarihinde kaynağından arşivlendi. Erişim tarihi: 8 Ağustos 2011.
- ^ a b Nelson, Roger, "Euler's triangle inequality via proof without words," Mathematics Magazine 81(1), February 2008, 58-61.
- ^ Johnson, Roger A., Advanced Euclidean Geometry, Dover, 2007 (orij. 1929), s. 189, #298(d).
- ^Coxeter, H.S.M. (1969). "Chapter 1". Introduction to geometry. Wiley. s. 12–13. ISBN 0471504580.
- ^Megiddo, N. (1983). "Linear-time algorithms for linear programming in R3 and related problems". SIAM Journal on Computing. 12 (4). ss. 759-776. doi:10.1137/0212052.
- Kimberling, Clark (1998). "Triangle centers and central triangles". Congressus Numerantium. Cilt 129. ss. i-xxv, 1-295.
- ^Pedoe, Dan (1988). Geometry: a comprehensive course. Dover.




































![{\displaystyle \mathrm {R} \left(s\right)=\mathrm {P_{c}} +\cos \left({\frac {\mathrm {s} }{\mathrm {r} }}\right)\left(P_{0}-P_{c}\right)+\sin \left({\frac {\mathrm {s} }{\mathrm {r} }}\right)\left[{\hat {n}}\times \left(P_{0}-P_{c}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1c6c1115dde943f477602b69e5a0cba324c4031)


