Karmaşık sayı
Bu madde hiçbir kaynak içermemektedir. (Ağustos 2012) (Bu şablonun nasıl ve ne zaman kaldırılması gerektiğini öğrenin) |
Matematikte karmaşık sayı, bir gerçel bir de sanal kısımdan oluşan bir nesnedir.[1] a ve b sayıları gerçek olursa karmaşık sayılar şu biçimde gösterilirler:
Karmaşık sayılar kümesi C şeklinde gösterilir. . özelliğini sağlayan sanal birime denir. Kimi zaman özellikle elektrik mühendisliğinde yerine, kullanılır.
Ayrıca matematikte bu sayıların uzayı olarak gösterilir. Bu harfin seçilmesinin nedeni İngilizcede karmaşık sözcüğünün karşılığı olarak complex sözcüğünün kullanılmasıdır, nitekim bazı Türkçe kaynaklarda complex sözcüğünden devşirilen kompleks sözcüğüne de raslanabilir. Karmaşık sayılara böyle bir adın verilmesinin nedeni ise aşağıda da göreceğimiz gibi gerçel ve sanal kısımların bir arada durmasıdır.
Bütün gerçel sayılar sanal kısımları sıfıra eşit olan birer karmaşık sayı olarak düşünülebilir. Diğer bir deyişle gerçel sayılar, karmaşık sayı düzleminde gerçel sayılar ekseni üzerinde bulunurlar.
Bir z karmaşık sayısının gerçel ve sanal parçaları sırasıyla Re(z) ve Im(z) fonksiyonlarıyla gösterilir. Bütün bu tanımları ve özellikleri bir örnekte gösterelim. sayısı gerçel kısmı Re(4-7i)=4, sanal kısmı Im(4-7i)=-7 olan uzayında bir karmaşık sayıdır.Bunun dışında karmaşık sayıların başka özellikleri de vardır. Örneğin bir karmaşık sayı düzlemde bir vektör olarak temsil edilebilir.
Tanım[değiştir | kaynağı değiştir]
Karmaşık sayılar kümesi birçok şekilde tanımlanabilir. Aşağıdaki tanımların hepsi birbirine eşyapısaldır, yani yapısal olarak biri diğerinin yerine kullanılabilir. Bu yüzden aslında içerik olarak farklı olan aşağıda tanımlanan tüm kümeleri aynı harfle gösterdik, . Ayrıca bu simge, sadece karmaşık sayılar dediğimiz öğeleri içeren bir küme olmaktan ötedir, üzerine tanımlayacağımız iki tane ikili işlemi olan bir cisimdir. Üstelik bu cisim, gerçel sayıların en büyük cisim genişlemesidir, yani gerçel sayıları bundan daha fazla genişletemeyiz. Gerçel sayılarla karmaşık sayıların aynı kardinaliteye (öğe sayısına) sahip olduğunu da unutmayalım.
Kartezyen uzay tanımı[değiştir | kaynağı değiştir]
Gerçek sayılar kümesinde her sayıyı ile çarparsak elde ettiğimiz kümesi önceki kümesine eşyapısaldır. Karmaşık sayılar cismi ise buradan hareketle
olarak tanımlanmış olur. Bu 2 boyutlu kartezyen uzay, Argand düzlemi olarak anılır. Eğer yerine tam sayılar cismi alınırsa oluşan karmaşık tam sayılar Gauss düzlemindedir. Bu sayılara da Gauss sayıları denir.
Karmaşık sayılar, bu tanımla aşağıdaki gibi ifade edilir: olmak üzere;[2]
Burada açıkça ve dir.
Cisim genişlemesi tanımı[değiştir | kaynağı değiştir]
Karmaşık olmayan sayılar, gerçel sayılar cisminin bir cisim genişlemesidir. sayısı polinomunun köklerinden biridir ve diğer kökü de olur. Bu iki öğenin gerçel sayılarla olan genişlemesinin eşyapısal olduğu kolaylıkla görülebilir:
Bu durumda
olarak tanımlanır. Daha açık olarak, karmaşık sayılar gerçel sayılar polinom halkasının polinomuyla üretilen bölüm halkasıdır:
Bu bölüm halkasında X öğesinin görüntüsü karmaşık birimidir. Bu sayede karmaşık sayılar halkası cebirsel olarak kapalı olur ki bu, gerçel sayıların cebirsel kapanışıdır. Cebirin temel teoremi bunu gerektirir, n dereceli her polinomun tam n kökü vardır. Biz, her karmaşık sayının olarak ifade edildiği bu tanıma daha âşinâyız.
Karmaşık düzlem[değiştir | kaynağı değiştir]

Karmaşık sayı, iki boyutlu kartezyen koordinat sisteminde, nokta veya konum vektörü olarak gösterilebilir. Sayılar alışıla geldiği gibi yatay bileşen gerçel kısmı ve düşey (dikey) bileşende sanal kısmı olarak çizildi (Şekil 1'e bakınız). Bu iki kısım karmaşık bir sayıyı ifade etmek için kullanılır ve bu yüzden Kartezyen-, dikdörtgensel- veya cebirsel form olarak adlandırılır.
İşlemlerin geometriksel açıklaması[değiştir | kaynağı değiştir]
Cebirsel olarak ifade edilen işlemler yukarıdaki karmaşık düzlem kullanılarak gösterilebilir.
 |
X = A + B: Karmaşık düzlemdeki A ve B gibi iki noktanın 'toplamı, X = A + Bdir ve köşeleri 0,A, B olan bir üçgendir. X, B, A ile benzerdir. Bu iki karmaşık sayı, vektör uzayında aynı katkıya sahiptir. |
 |
X = AB: A ve B gibi iki noktanın çarpımı X = ABdir ve köşeleri 0, 1, A olan bir üçgendir. 0, B, X benzer üçgenlerdir. |
 |
X = A*: A noktasının Karmaşık eşleniği, X = A*dır ve köşeleri 0, 1, Adır. 0, 1, Xnin ayna görüntüsüdür. |
Bu geometrik açıklamalar, cebirsek problemlerin geometriksel biçime dönüştürmeyi sağlar. Ve tam tersi de geçerlidir (geometriksel problemler, cebirsel olarak çözülebilir). Örneğin, geometriksel şekil olan onyedigen problemi, Gauss tarafından şu şekilde cebirsel denklem analizine dönüştürüldü:x17 = 1 (Çokgene bakınız).

fonksiyonunun alan renklendirme çizimi. Ton, fonksiyon değişkenini ifade ederken, doygunluk ve canlılık miktarı ifade eder.
Kutupsal form[değiştir | kaynağı değiştir]
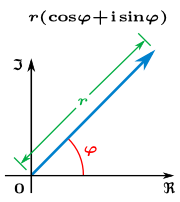
Diyagramlar çeşitli özellik gösteriler. Öncelikle Şekil 2'de r ile gösterilen orjin (merkez)den z noktasına olan uzaklık, mutlak değer olarak bilinir. Mutlak değer veya büyüklük olarak yazılır. Pisagor teoremine göre,
Karmaşık sayılar arasındaki uzaklık genellikle, fonksiyonu ile gösterilir. Bu fonksiyon, karmaşık sayıların metrik uzayına dönüşüdür. Limit ve süreklilik hakkında fikir verir. İki boyutlu uzayın tüm standart özellikleri karmaşık sayılar için geçerlidir. (tüm z ve w için, ).
İkinci olarak, şeklindeki karmaşık sayının argümanı veya fazı, reel eksenle yaptığı açıdır (Şekil 2'de φ olarak gösteriliyor) ve olarak yazılır. Mutlak değer olarak, argüman dikdörtgensel formdan elde edilebilir :
- veya ( olduğunda π ekleyerek, olur).
φ değeri, 2π'nin herhangi çarpanı olarak değiştirilebilir ve yine aynı açıyı verir (burada radyan kullanıldığına dikkat ediniz). Bundan dolayı, arg fonksiyonu bazen çok değerli olarak ifade edilir, Fakat çoğunlukla değer veya aralığında seçilir (Bu asıl değerdir).
Karmaşık sayıların çeşitli formlarda gösterilebilir. Kutupsal form, bir düzlemdeki noktanın tam konumunu belirten mutlak değer ve argüman bileşenleri olarak gösterilebilir, şöyle ki; (r,φ) kutupsal çiftlerinden, özgün dikdörtgenin koordinatları olan elde edildi). Diğer gösterimi:
buna trigonometrik form denir ve bazen r cis φ olarak kısaltılır. Euler formülü kullanılarak şu şekilde gösterilebilir:
buna da üstel form denir. Elektrik Mühendisliği'nde daha çok açısal gösterim kullanımı yaygındır. Bu gösterim, A genlikli ve θ fazına sahip fazörü ifade eder ve şu şekilde yazılır:
Açısal gösterimde θ, hem radyan hem de derece olabilir. Elektrik akımını ifade eden i ile karıştırmamak için, Elektrik Mühendisliği'nde i yerine daha çok j kullanılır.
Kutupsal formdaki işlemler[değiştir | kaynağı değiştir]
Çarpma ve bölme kutupsal formda temel formüllere sahiptir:
ve
Bu formda her iki çarpanın (eşitliklerin solundakiler) katsayıları çarpımın özelliğinden dolayı yan yana (çarpma işleminde) veya alt alta (bölme işleminde) getirilebilirler. Diğer yandan üslü sayıların kuralları gereği ifadeler aynı ise (burada ), bunlar aynı ifade altına alınırken çarpma işleminde üsler toplanır, bölme işleminde ise üsler çıkartılır.
Üs tam sayı ise şöyle gösterilir:
Sonuç olarak kutupsal formlar kökleri bulmak içinde kullanılabilir. z herhangi karmaşık sayı olmak üzere ve n pozitif tam sayı için zn = c olarak gösterilebilir. Bu da cnin n. kökü diye okunur. Eğer c sıfır değilse, tam n tane farklı c nin kökü vardır (cebirin temel teoremine göre). r > 0 için, c = re iφ'de c nin n. kökleri:
Burada , pozitif reel sayı olan r nin genellikle pozitif olan n. kökünü ifade eder. Eğer c = 0, ise c nin tek bir kökü vardır, o da 0'dır.
Karmaşık sayılarda işlem[değiştir | kaynağı değiştir]
Karmaşık sayılarda cebirsel işlemler gerçel sayıların genişlemesidir.[2] Öncelikle iki karmaşık sayının eşitliğini verelim.
Eşitlik[değiştir | kaynağı değiştir]
Bir ve karmaşık sayıları için
- ancak ve iken geçerlidir.bu doğru bir kavramdır...
Toplama[değiştir | kaynağı değiştir]
Bir ve karmaşık sayıları için
Çarpma[değiştir | kaynağı değiştir]
Bir ve karmaşık sayıları için
Eşlenik[değiştir | kaynağı değiştir]

Bir karmaşık sayısı için eşlenik ifadesi dönüşümüdür ve
ya da matrislerde
olarak tanımlanır.
Eşleniğin cebirsel özellikleri[değiştir | kaynağı değiştir]
- ancak z gerçel sayı olduğunda geçerlidir.
Çarpımsal ters[değiştir | kaynağı değiştir]
Bir karmaşık sayısının tersi ancak
olarak ya da bir matrisin tersine uygun olarak
olduğu görülür.
Karmaşık sayının karekökü
burada İşaret fonksiyonudur.
Karmaşık sayının n dereceden kökü
Kök derecesi iki den büyük olan karmaşık sayıların genel denklemi uzundur. n sayısı artıkça genel denklemde uzar. Trigonometrik ve üstel biçim daha uygundur.
için tam sayı olmak üzere
Üstel biçim :
Trigonometrik biçim :
kök derecesinin bir eksiği kadar sıfırdan başlayarak tam sayılar verilebilir. Bu da n dereceden alınan karmaşık sayının köklerini verir.
Ayrıca bakınız[değiştir | kaynağı değiştir]
- Karmaşık analiz
- Hiperbolik sayılar
- Çifte karmaşık sayılar (bicomplex numbers)
- Dörtlük sayılar (Quaternions)
- Sekizlik sayılar (Octonions)
Başvuru ve Kaynaklar[değiştir | kaynağı değiştir]
- Notlar
- ^ Matematik ve Oyun. Ali Nesin. Nesin Yayıncılık. 2007. s. 189. 11 Ocak 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 10 Ocak 2021.
- ^ a b Andreescu, Titu; Andrica, Dorin (17 Şubat 2014). Complex Numbers from A to ... Z (İngilizce). Springer Science & Business Media. ss. 1-10. ISBN 978-0-8176-8415-0.
- Kaynakça
- A. Mostowski & M. Stark, Introduction to Higher Algebra. Pergamon Press. New York: 1964.
- "Karmaşık Sayılar". Matematik Dünyası Dergisi. s. 64-73. 8 Ağustos 2020 tarihinde kaynağından arşivlendi.




















![{\displaystyle \scriptstyle \mathbb {C} \equiv \scriptstyle \mathbb {R} [X]/(X^{2}+1)\equiv \{\,a+\mathbf {i} b\,|\,a,b\in \scriptstyle \mathbb {R} \,\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b17c8c56bc2a1324c74a87201567fd1b97207c4)

















![{\displaystyle (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)









![{\displaystyle \left\{{\sqrt[{n}]{r}}\,e^{i\left({\frac {\varphi +2k\pi }{n}}\right)}\mid k\in \{0,1,\ldots ,n-1\}\,\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/650bb56174c0c0f2a6adb9c7eafcca3c9ad0a19f)
![{\displaystyle {\sqrt[{n}]{r}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10eb7386bd8efe4c5b5beafe05848fbd923e1413)

















![{\displaystyle {\sqrt {x+i.y}}=\pm {\frac {1}{\sqrt {2}}}\left[{\sqrt {x+{\sqrt {x^{2}+y^{2}}}}}+{\frac {i.y.\operatorname {sgn}(y)}{\sqrt {x+{\sqrt {x^{2}+y^{2}}}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/405ae90651ff53056dc7292ace58202b3044ad9f)


![{\displaystyle {\sqrt[{n}]{x+i.y}}={\sqrt[{2n}]{x^{2}+y^{2}}}.e^{\frac {i.(\arctan({\frac {y}{x}})+2k.\pi )}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de3382cdc995ad841c1446693f294d860ce4f880)
![{\displaystyle {\sqrt[{n}]{x+i.y}}={\sqrt[{2n}]{x^{2}+y^{2}}}.\left\{\cos \left[{\frac {\arctan({\frac {y}{x}})+2k.\pi }{n}}\right]+i.\sin \left[{\frac {\arctan({\frac {y}{x}})+2k.\pi }{n}}\right]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d95aaf9b44ef80fef03574d711fdc5f746f2543)











