Rasyonel sayılar


Rasyonel sayılar, iki tam sayı arasındaki oranı temsil eden, bir pay p ve sıfırdan farklı bir payda q olmak üzere, bir bölme işlemi veya kesir formunda ifade edilebilen sayıları tanımlar.[1] Örneğin, rasyonel bir sayı olarak kabul edilir, bu kapsamda her tam sayı da (mesela, gibi) rasyonel sayılar kategorisindedir. Rasyonel sayılar kümesi, çoğunlukla kalın harf biçimindeki Q veya karatahta vurgusu kullanılarak şeklinde ifade edilir.[a]
Rasyonel sayı, reel sayılar kümesine ait bir sayıdır. Bu sayılar, ondalık açılımlarının sonlu sayıda rakam içermesiyle karakterize edilir ve bu açılım ya bir noktadan sonra sonlanır (örneğin: 3/4 = 0.75) ya da belirli bir dizinin rakamlarının sürekli olarak tekrar edilmesiyle devam eder (örneğin: 9/44 = 0.20454545...).[2] Bu özellik, yalnızca on tabanlı sistemde geçerli olmayıp, ikili, on altılı gibi diğer tüm tam sayı taban sistemlerinde de geçerlidir.
Rasyonel olmayan bir reel sayı, irrasyonel olarak tanımlanır.[3] Bu kapsamda irrasyonel sayılara örnek olarak Karekök 2 (), π, e ve altın oran (φ) gösterilebilir. Rasyonel sayılar kümesinin sayılabilir bir yapıda olması ve reel sayılar kümesinin ise sayılamaz bir yapıya sahip olması sebebiyle, reel sayıların büyük bir çoğunluğu irrasyoneldir.[4]
Rasyonel sayılar, belirli tam sayı çiftleri olan (p, q) için, q ≠ 0 koşulu altında, eşdeğerlik sınıfı olarak formel bir şekilde ifade edilebilir. Bu çerçevede, eşdeğerlik ilişkisi şu şekilde tanımlanır:
Bu bağlamda, kesri, belirtilen (p, q) çiftinin eşdeğerlik sınıfını temsil eder.[5]
Rasyonel sayılar tam sayıların bir genişlemesidir. kümesi genelde şöyle tanımlanır:
(a ve b tam sayı ve b sıfır olmamak üzere a/b şeklindeki sayılara rasyonel sayı denir)
ve veya eşdeğer rasyonel sayılardır. Dolayısıyla her rasyonel sayı sonsuz şekilde ifade edilebilir. Rasyonel sayıların en basit biçimi ve tam sayılarının ortak bölen'inin olmadığı ifadesidir.[6]
Her tam sayı rasyonel sayıdır. Çünkü veya veya şeklinde yani rasyonel sayı tanımına uygun biçimde yazılabilirler. Rasyonel sayılar kümesi , tam sayılar kümesi 'yi kapsar. Yani .
Daha ince bir tanımı ise tam sayılar üzerinden tanımlanacak bir denklik bağıntısıyla yapılabilir. Böylece her denklik sınıfı bir rasyonel sayı olarak anılır. kümesinden seçilmiş keyfi (a,b) ve (c,d) ögeleri için "~" bağıntısı olarak tanımlansın. Bunun bir denklik bağıntısı olduğu kolaylıkla kanıtlanabilir. Bu durumda, denklik sınıfları olurlar. Rasyonel sayı ise basitçe şeklinde tanımlanır. Tanımda paydanın sıfır olmama şartı ifadesinin tanımlanmamış olmasındandır. Bir sayının sıfıra bölümü tanımsızdır.[7]
Sıfırdan büyük olan rasyonel sayılara pozitif rasyonel sayılar, sıfırdan küçük rasyonel sayılar da negatif rasyonel sayılar denir. Pozitif rasyonel sayılar kümesi ile, negatif rasyonel sayılar kümesi ile gösterilir.
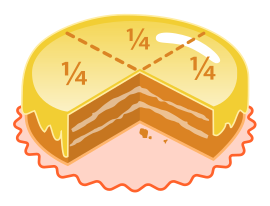
Yandaki şekilde, bir yuvarlak pasta 4 eş parçaya bölünmüş ve bu 4 eş parçalardan her birisi olarak görülmektedir. Ancak bir parça alınmış olduğundan kalan eksikdir. Geriye kalan, dört eşit parçaya bölünmüş bütünün üç tane parçası (yani 3'te 4 oranı) veya (kesiri)dir. Bu ifadesi şeklinde gösterilir. Burada ifadede kesir çizgisinin üstündeki değere (yani 3'e) pay, kesir çizgisinin altındaki değere (yani 4’e) payda denir. Bu kesir, “üç bölü dört” ya da “dörtte üç” diye okunur.
Rasyonel sayılar, toplama ve çarpma işlemleri ile birleştirildiğinde, tam sayıları barındıran ve aynı zamanda tam sayılar içeren herhangi bir matematiksel cismin (İng. field) bir parçası olan bir cismi meydana getirir. Bu bağlamda, rasyonel sayılar cismi bir asal cisim niteliğindedir ve bir cismin sıfır karakteristiğe sahip olması, yalnızca o cismin rasyonel sayıları bir alt cisim olarak barındırması ile mümkündür. 'nun sonlu genişlemeleri cebirsel sayı cisimleri olarak isimlendirilir ve 'nun cebirsel kapanışı, cebirsel sayılar cismidir.[8]
Matematiksel analiz çerçevesinde, rasyonel sayılar, reel sayılar içerisinde yoğun bir alt küme teşkil eder. Reel sayıların tanımlanması, rasyonel sayılar baz alınarak, Cauchy dizileri, Dedekind kesitleri veya sonsuz ondalık sayılar kullanılarak gerçekleştirilebilir.
Terminoloji[değiştir | kaynağı değiştir]
"Rasyonel" terimi, kümesine yapılan atıflarda, bir rasyonel sayının iki tam sayının oranını temsil etmesi gerçeğine işaret eder. Matematik alanında "rasyonel", sıklıkla "rasyonel sayı" teriminin kısaltması olarak kullanılmaktadır. "Rasyonel" sıfatı, zaman zaman katsayıların rasyonel sayılar olduğunu ifade eder. Mesela, rasyonel koordinatlara sahip bir nokta rasyonel nokta olarak adlandırılır; rasyonel sayılardan oluşan bir matrise rasyonel matris denir; rasyonel katsayılara sahip bir polinoma rasyonel polinom denilebilir, ancak "rasyoneller üzerinde bir polinom" ifadesi, "rasyonel ifade" ile "rasyonel fonksiyon" arasındaki muhtemel karışıklıkları engellemek amacıyla genellikle tercih edilir. Bununla birlikte, rasyonel eğri, rasyoneller üzerinde tanımlanmış bir eğri anlamına gelmez; bunun yerine rasyonel fonksiyonlarla parametrize edilebilen bir eğriyi ifade eder.
Etimoloji[değiştir | kaynağı değiştir]
Günümüzdeki "rasyonel sayılar", "rasyo" ("oran") kavramları ile ilişkilendirilse de, "rasyonel" sözcüğü, "rasyo" teriminin bir türevi olmayıp, tam tersine, "rasyo" sözcüğü "rasyonel"den kaynaklanmaktadır. "Rasyo" (İng. ratio) teriminin çağdaş anlamda ilk kez kullanıldığı dönem İngilizcede yaklaşık olarak 1660 yılına dayanırken, "rasyonel" ifadesinin sayıları tanımlama amacıyla kullanımı bu tarihten yaklaşık bir yüzyıl önce, 1570 yılında meydana gelmiştir.[9] "Rasyonel" teriminin bu özel anlamı, "irrasyonel" teriminin matematiksel bağlamda ilk kullanımından, yani 1551 yılından türemiş olup, Öklit'in eserlerinin çevirilerinde özgün kullanımını izleyerek (Grekçe: ἄλογος) kullanılmıştır.[9][10]
Bu alışılmadık tarihi olgular zinciri, antik Yunan matematikçilerinin, kendilerini irrasyonel olarak nitelendirilen uzunlukları sayı olarak kabul etmekten çekinerek, böylece sapkınlıktan uzak durmayı tercih etmelerinden kaynaklanmaktadır.[11] Dolayısıyla, bu tür uzunluklar, konuşulmaması gereken, yani Yunancada (Grekçe: ἄλογος) ifade edilen mantıksız anlamına gelen irrasyonel kelimesi ile tanımlanmıştır.[12]
Aritmetik[değiştir | kaynağı değiştir]
olmak üzere:
İndirgenemez kesir[değiştir | kaynağı değiştir]
Her bir rasyonel sayı, şeklinde, a ve b aralarında asal tam sayılar olmak üzere ve b > 0 koşuluyla, indirgenemez kesir olarak eşsiz bir biçimde gösterilebilir. Bu durum, genellikle rasyonel sayının kanonik formu olarak isimlendirilir.
Bir rasyonel sayının başlangıç noktasından kanonik formuna ulaşılması, a ve b'yi onların en büyük ortak bölenine bölerek ve eğer b < 0 ise, elde edilen pay ve paydanın işaretinin değiştirilmesi işlemiyle mümkün olmaktadır.
Tam sayı ifadelendirme[değiştir | kaynağı değiştir]
Her bir tam sayı n, rasyonel bir sayı biçiminde olarak gösterilebilir ki bu, rasyonel sayılar bağlamında onun kanonik formunu temsil eder.
Eşitlik ilkesi[değiştir | kaynağı değiştir]
- ifadesi, ancak ve ancak olduğunda doğrudur.
Her iki kesir de kanonik forma sahip olduğunda:
- , ancak ve ancak ve eşitlikleri sağlandığında geçerli olur.[5]
İki rasyonel sayının eşitliği, o sayıların pay ve paydalarının rasyonel olmasıyla anlaşılır. olmak üzere ve iki rasyonel sayı ise bu iki sayı ancak olduğunda eşittir.
Bu koşul, yukarıdaki tanımdan çıkartılabilir. İki rasyonel sayı aynı denklik sınıfındaysa birbirine eşittir, Denklik bağıntısı da zaten koşulunu içermekteydi.
Sıralama[değiştir | kaynağı değiştir]
Eğer her iki paydanın da pozitif olduğu durumlar (özellikle her iki kesirin kanonik formda olduğu durumlar) göz önüne alınırsa:
- ancak ve ancak şeklinde olur.
Diğer yandan, paydalardan biri negatifse, negatif paydaya sahip her kesirin önce pozitif bir paydaya sahip eşdeğer bir forma dönüştürülmesi gerekir—bunun için hem payının hem de paydasının işaretinin değiştirilmesi gerekir.[5]
Paydaları eşit olan rasyonel sayılar[değiştir | kaynağı değiştir]
- Paydaları eşit olan rasyonel oranlar için payı büyük olan daha büyük, payı küçük olan daha küçüktür.
- Örneğin
- Burada paydalar eşit ve yirmidir. Pay değerleri karşılaştırılınca soldaki pay 7 sağdaki pay 3'ten daha büyük olduğu için, soldaki rasyonel oran daha büyüktür.
- Unutmamalıdır ki negatif paylar karşılaştırılırken sadece mutlak değerlerin karşılaştırılması hatalı olup negatif işaretlerinin de ele alınması ve :negatif sayılı pay değerlerde mutlak değeri büyük görünen sayının daha küçük olduğu hatırlanmalıdır:
- Payda 20'ye eşit olup sağdaki negatif pay değeri -3, soldaki negatif pay değeri olan -7'den daha büyük olduğu için sağdaki oran daha büyüktür.
Payları eşit olan rasyonel sayılar[değiştir | kaynağı değiştir]
- Payı eşit olan rasyonel sayılar için ise paydaları eşit olanın tam tersi bir kural uygulanır:
- Paylar eşit olduğunda bölünen parça sayısı yani payda büyüdükçe oluşan parça boyutları daha küçük olacaktır.
Payları ya da paydaları eşit olmayan rasyonel sayılar[değiştir | kaynağı değiştir]
- Bu şekildeki durumlarda karşılaştırmadan evvel paydaların eşitlenmesi veya içler dışlar çarpımı yapılmasını gerektirir.
- Paydaların eşitlenmesi
- Her iki rasyonel sayının da birbirlerinin paydalarıyla genişletilmesini gerektirir.
- Paydaların eşitlenmesi
- Yukarıda görüldüğü gibi genişletme işleminden sonra oluşan paydaların ikisi de yani 40'tır. Yukarıda görüldüğü gibi karşılaştırılabilir.
- İçler dışlar çarpımı
- Birinci rasyonel sayının payının ikincinin paydasına, ikincinin paydasının ise birincinin payıyla çarpılmasıdır:
- İçler dışlar çarpımı
- .
Toplama[değiştir | kaynağı değiştir]
İki kesrin toplanması şu şekilde gerçekleştirilir:
Eğer her iki kesir de kanonik formdaysa, sonuç ancak ve ancak b, d aralarında asal tam sayılar olması durumunda kanonik formda olacaktır.[5][13]
Çıkarma[değiştir | kaynağı değiştir]
Eğer her iki kesir de kanonik formdaysa, sonuç ancak ve ancak b, d aralarında asal tam sayılar ise kanonik formdadır.[13]
Çarpma[değiştir | kaynağı değiştir]
Çarpma kuralı şu şekildedir:
burada sonuç, her iki orijinal kesir de kanonik formda olsa bile, bir indirgenebilir kesir olabilir.[5][13]
Tersi[değiştir | kaynağı değiştir]
Herhangi bir rasyonel sayı , sıklıkla tersi olarak ifade edilen bir toplamın tersine sahiptir,
- .
kanonik formda ise, onun karşıtının da kanonik formda olması aynı şekilde geçerlidir.
Sıfırdan farklı bir rasyonel sayı , tersi olarak da adlandırılan bir çarpımın tersine sahiptir,
kanonik formda bulunuyorsa, onun tersinin kanonik formu, a değerinin işaretine göre ya ya da şeklinde olur.
Bölme[değiştir | kaynağı değiştir]
Eğer b, c, d sıfırdan farklıysa, bölme kuralı şu şekildedir:
Böylece, 'yi ile bölmek, 'yi 'nin tersi ile çarpmakla eşdeğerdir:[13]
Tam sayı kuvvetine üs alma[değiştir | kaynağı değiştir]
n negatif olmayan bir tam sayı olduğunda,
Sonuç, için aynı şekilde kanonik formda bulunuyorsa, kanonik formdadır. Belirli bir durum olarak,
Eğer a ≠ 0, o zaman
Eğer kanonik formdaysa, sonucun kanonik formu a > 0 veya n çift ise olacaktır. Aksi takdirde, sonucun kanonik formu olur.
Sürekli kesir gösterimi[değiştir | kaynağı değiştir]
Bir sonlu sürekli kesir ifadesi, aşağıdaki formda gösterilebilir:
bu ifadede, an tam sayıları temsil eder. Herhangi bir rasyonel sayı , katsayıları an, (a, b) çifti üzerine Öklid algoritması uygulanarak elde edilebilen bir sonlu sürekli kesir olarak gösterilebilir.
Diğer gösterimler[değiştir | kaynağı değiştir]
- Bayağı kesir:
- Karmaşık sayı:
- Bir bağ çizgisi kullanılarak devirli sayı ile:
- Parantez kullanılarak devirli sayı ile:
- Geleneksel tipografi kullanılarak sürekli kesir:
- kısaltılmış notasyon ile sürekli kesir:
- Mısır kesri:
- Asal üs ayrışımı:
- Tırnak notasyonu:
aynı rasyonel değeri temsil etmenin farklı yollarıdır.
Tanım[değiştir | kaynağı değiştir]

Rasyonel sayılar, tam sayıların sıralı çiftlerine dayanan denklik sınıfları biçiminde kurulabilir.[5][13]
Daha kesin bir ifadeyle, kümesi, n ≠ 0 olacak şekilde tam sayıların (m, n) çiftlerinin kümesi olarak alınsın. Bu küme üzerinde bir denklik bağıntısı
Toplama ve çarpma işlemleri aşağıdaki kurallarla tanımlanabilir:
Bu denklik ilişkisi, daha önce tanımlanmış toplama ve çarpma işlemleriyle uyumlu bir kongrüans ilişkisi olarak işlev görür; böylece rasyonel sayılar kümesi , bu denklik ilişkisine göre tanımlanan bölüm kümesi, formunda, söz konusu işlemler aracılığıyla türetilmiş toplama ve çarpma işlemleriyle zenginleştirilmiştir. (Bu yapı, herhangi bir tam bölge kullanılarak oluşturulabilir ve söz konusu bölgenin kesirler cismini meydana getirir.)[5]
Bir (m, n) çiftinin denklik sınıfı, şeklinde ifade edilir. (m1, n1) ve (m2, n2) çiftleri, ancak ve ancak eğer
ise aynı denklik sınıfına dahildir (yani eşdeğerdirler). Bu durum,
- olduğunda mümkündür.
Her denklik sınıfı , sonsuz sayıda çift tarafından temsil edilebilir, çünkü
Her denklık sınıfı, benzersiz bir kanonik temsilci elemanı içerir. Kanonik temsilci, denklik sınıfındaki (m, n) benzersiz çiftidir öyle ki m ve n aralarında asaldır ve n > 0. Bu, rasyonel sayının en düşük terimlerle temsili olarak adlandırılır.
Tam sayılar, tam sayı n'yi rasyonel sayı ile özdeşleştirerek rasyonel sayılar olarak düşünülebilir.
Rasyonel sayılar üzerinde, tam sayıların doğal sıralamasını genişleten bir tam sıralama tanımlanabilir. Buna göre
Eğer
Özellikler[değiştir | kaynağı değiştir]
Yukarıda gösterilen toplama ve çarpma işlemleriyle birlikte, tüm rasyonel sayıların kümesi , bir alan oluşturur.[5]
, özdeşlik dışında hiçbir alan otomorfizmine sahip değildir. (Bir alan otomorfizmi 0 ve 1'i sabit tutmalıdır; iki sabit elemanın toplamını ve farkını sabit tutmak zorunda olduğundan, her tam sayıyı sabit tutmalıdır; iki sabit elemanın bölümünü sabit tutmak zorunda olduğundan, her rasyonel sayıyı sabit tutmalı ve dolayısıyla özdeş olmalıdır.)
, kendisi dışında alt alanı olmayan bir asal alandır.[14] Rasyoneller, sıfır karakteristiğe sahip en küçük alandır. Sıfır karakteristiğe sahip her alan, ile izomorfik benzersiz bir alt alana sahiptir.
Yukarıda tanımlanan sırayla, , kendisi dışında alt alanı olmayan bir sıralı alandır ve her sıralı alanın, ile izomorfik benzersiz bir alt alanı içerdiği anlamında en küçük sıralı alandır.[13]
, tam sayıların kesirler alanıdır. 'nun cebirsel kapanışı, yani rasyonel polinomların köklerinin alanı, cebirsel sayılar alanıdır.
Rasyonel sayılar, yoğun sıralanmış bir kümedir: herhangi iki rasyonel sayı arasında başka bir rasyonel sayı bulunur ve dolayısıyla sonsuz sayıda başka rasyonel sayı bulunur. Örneğin,
( pozitif olmak üzere) şeklindeki herhangi iki kesir için,
En küçük veya en büyük elemanı olmayan, sayılabilir, yoğun (yukarıdaki anlamda) ve tamamen sıralı bir küme, rasyonel sayılarla sıra izomorfiktir.[15]
Sayılabilirlik[değiştir | kaynağı değiştir]

Tüm rasyonel sayılar kümesinin sayılabilir olduğu, sağ tarafta yer alan gösterim ile açıklanmıştır. Her bir rasyonel sayının, iki tam sayının oranı şeklinde ifade edilebilme özelliği göz önünde bulundurulduğunda, kare kafes üzerindeki her bir noktaya, bir Kartezyen koordinat sistemi benzeri bir yaklaşımla, iki tam sayı atanması mümkündür; böylelikle her bir kafes noktası bir rasyonel sayı ile ilişkilendirilebilir. Bu yöntem, sağlanan grafikte kırmızı ile işaretlenmiş olan, birçok farklı kafes noktasının aynı rasyonel sayıyı temsil etmesi gibi bir fazlalığın ortaya çıkmasına neden olmaktadır. Bu fazlalığın bir örneği, sağ alt köşeye doğru diagonal bir hat üzerinde gözlemlenebilir; bu tür oranlar, herhangi bir sıfırdan farklı sayının kendisi ile bölünmesi durumunda daima bir değerini alacaktır.
Bu tür fazlalıklar olmadan tüm rasyonel sayıların tanımı mümkündür: örnekler arasında Calkin-Wilf ağacı ve Stern-Brocot ağacı bulunmaktadır.
Tüm rasyonel sayılar kümesi sayılabilir olduğu ve tüm reel sayılar kümesi (aynı zamanda tüm irrasyonel sayılar kümesi) sayılamaz olduğu için, rasyonel sayılar kümesi bir null kümesidir, yani Lebesgue ölçümü anlamında neredeyse tüm reel sayılar irrasyoneldir.
Reel sayılar ve topolojik özellikler[değiştir | kaynağı değiştir]
Rasyonel sayılar, reel sayıların yoğun bir alt kümesidir; her reel sayının yanında keyfi olarak yakın rasyonel sayılar vardır.[5] İlgili bir özellik, rasyonel sayıların, sürekli kesir olarak sonlu genişlemelere sahip tek sayılar olmasıdır.[16]
Reel sayıların alışılageldik topolojisi içinde, rasyonel sayılar ne bir açık küme ne de bir kapalı kümedir.
Sıralarının bir sonucu olarak, rasyonel sayılar bir sıra topolojisi taşır. Rasyonel sayılar, reel sayıların bir alt uzayı olarak, ayrıca bir altuzay topolojisi taşır. Rasyonel sayılar, mutlak fark metriği kullanılarak bir metrik uzay oluşturur ve bu, üzerinde üçüncü bir topoloji sağlar. Bu üç topoloji çakışır ve rasyonelleri bir topolojik alana dönüştürür. Rasyonel sayılar, yerel kompakt uzay olmayan bir uzayın önemli bir örneğidir. Rasyoneller, topolojik olarak, izole noktası olmayan benzersiz sayılabilir ölçülebilir uzay olarak nitelendirilir. Uzay ayrıca tamamen bağlantısızdır. Rasyonel sayılar, tam metrik uzay oluşturmaz ve reel sayılar, yukarıda verilen metrik altında 'nun tamamlanmasıdır.
p-sel sayılar[değiştir | kaynağı değiştir]
Yukarıda bahsedilen mutlak değer metriğine ek olarak, 'yu bir topolojik alan haline getiren diğer metrikler de vardır:
p bir asal sayı olsun ve sıfırdan farklı herhangi bir tam sayı a için, burada pn a'yı bölen p'nin en yüksek kuvvetidir.
Ayrıca olarak belirleyelim. Herhangi bir rasyonel sayı için,
- olarak belirleyelim.
O zaman
üzerinde bir metrik tanımlar.[17]
Metrik uzay tam değildir ve tamamlanmış hali p-adik sayı alanı 'dir. Ostrowski teoremi, rasyonel sayılar üzerindeki herhangi bir önemli mutlak değerin, ya alışılagelmiş reel mutlak değere ya da bir p-adik mutlak değere eşdeğer olduğunu belirtir.
Ayrıca bakınız[değiştir | kaynağı değiştir]
Not listesi[değiştir | kaynağı değiştir]
Kaynakça[değiştir | kaynağı değiştir]
- ^ Rosen, Kenneth (2007). Discrete Mathematics and its Applications (6 bas.). New York, NY: McGraw-Hill. ss. 105, 158-160. ISBN 978-0-07-288008-3.
- ^ "Rational number". Encyclopedia Britannica (İngilizce). 11 Aralık 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Ağustos 2020.
- ^ Weisstein, Eric W. "Rational Number". Wolfram MathWorld (İngilizce). 14 Temmuz 2023 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Ağustos 2020.
- ^ Rosen, Kenneth (2007). Discrete Mathematics and its Applications (6 bas.). New York, NY: McGraw-Hill. ss. 105, 158-160. ISBN 978-0-07-288008-3.
- ^ a b c d e f g h i j k l Biggs, Norman L. (2002). Discrete Mathematics. India: Oxford University Press. ss. 75-78. ISBN 978-0-19-871369-2.
- ^ Robinson, Julia (1996). The Collected Works of Julia Robinson (İngilizce). American Mathematical Soc. ISBN 978-0-8218-0575-6.
- ^ Lass, Harry (18 Kasım 2009). Elements of Pure and Applied Mathematics (İngilizce). Courier Corporation. ISBN 978-0-486-47186-0.
- ^ Gilbert, Jimmie; Linda, Gilbert (2005). Elements of Modern Algebra (6.6yayıncı=Thomson Brooks/Cole bas.). Belmont, CA. ss. 243-244. ISBN 0-534-40264-X.
- ^ a b Oxford English Dictionary (2.2tarih=1989 bas.). Oxford University Press.
- ^ Shor, Peter (9 Mayıs 2017). "Does rational come from ratio or ratio come from rational". Stack Exchange (İngilizce). 17 Nisan 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 19 Mart 2021.
- ^ Coolman, Robert (29 Ocak 2016). "How a Mathematical Superstition Stultified Algebra for Over a Thousand Years" (İngilizce). 21 Aralık 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 20 Mart 2021.
- ^ Kramer, Edna (1983). The Nature and Growth of Modern Mathematics. Princeton University Press. s. 28.
- ^ a b c d e f g h "Fraction - Encyclopedia of Mathematics". encyclopediaofmath.org. 27 Eylül 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 17 Ağustos 2021.
- ^ Sūgakkai, Nihon (1993). Encyclopedic Dictionary of Mathematics, Volume 1. London, England: MIT Press. s. 578. ISBN 0-2625-9020-4.
- ^ Giese, Martin; Schönegge, Arno (December 1995). Any two countable densely ordered sets without endpoints are isomorphic - a formal proof with KIV (PDF). 25 Kasım 2021 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 17 Ağustos 2021.
- ^ Anthony Vazzana; David Garth (2015). Introduction to Number Theory (2nd, revised bas.). CRC Press. s. 1. ISBN 978-1-4987-1752-6. Extract of page 1
- ^ Weisstein, Eric W. "p-adic Number". Wolfram MathWorld (İngilizce). 2 Mayıs 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 17 Ağustos 2021.
Dış bağlantılar[değiştir | kaynağı değiştir]
| Wikimedia Commons'ta Rasyonel sayılar ile ilgili ortam dosyaları bulunmaktadır. |

- Hazewinkel, Michiel, (Ed.) (2001), "Rational number", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104
- "Rational Number" From MathWorld – A Wolfram Web Resource










































































![{\displaystyle [2;1,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1887ebaaed6f055311780a6b5c6eb3c2d43481e7)








































