Hiperbolik sayılar
| × | 1 | j |
|---|---|---|
| 1 | 1 | j |
| j | j | 1 |
Gerçel sayılarda olmayan ve karesi 1 olan bir sayının kümeye katılmasıyla üretilen kümeye hiperbolik sayılar kümesi denir. Tıpkı karmaşık sayılarda olduğu gibi, hiperbolik sayılar şeklinde yazılabilen sayılardır, ancak karmaşık sayılardan tek farkı hiperbolik birim denilen sayının
olarak tanımlanmasıdır. Bu sayılar fizikte, özellikle Özel görelilikte sıkça kullanılmaktadır. Daha anlaşılır bir tanımını şöyle yapabiliriz.
- olduğuna göre,
- neden olmasın varsayımı ile açıklayabiliriz.
Buradan geriye dönük tüm tanımlanan sayıların aslında bir varsayımdan ibaret olabileceği çıkarımını yapabiliriz. Yani alınan matematiksel modele göre çözümler üretiyoruz. Eğer h gibi bir sayı varsa bu fiziksel bir olayı açıklamak içindir. Buradan şu anlaşılır fiziksel olayları açıklamak için matematiğe ihtiyaç vardır veya fizik matematiğin görüntülerinden ibarettir. Buradan doğadaki olayların hepsinin matematikten ibaret olduğunu anlarız. Matematik soyuttur ama fizik gibi somut bir yansıması vardır. Eğer matematik bir fiziksel olayı açıklayamıyorsa bu olay fiziksel değildir.
Resmî tanım[değiştir | kaynağı değiştir]
polinomunun kökleri 1 ve -1 iken, bunların dışında başka bir sayısının da bu polinomun bir kökü olduğunun varsayılmasıyla oluşan
bölüm halkasına hiperbolik sayılar kümesi denir ve genelde ya da H ile gösterilir.
Böyle bir sayının polinom halkasının katsayılar kümesi olan gerçel sayılar kümesi 'de de olmadığı görülebilir (ya da bu sayı yine 1 ya da -1 sayılardan birine eşit olmak zorunda kalır). Böylece bu sayı kümesi cebirin temel teoremi gereği bir cisim olamaz, değişmeli bir halka olur.
Tanım[değiştir | kaynağı değiştir]
Bir bölünmüş-karmaşık sayı gerçek sayıların sıralı bir çifti formunda burada x ve y gerçek sayılar ve j niceli uygundur
- seçilirse karmaşık sayı içindeki sonuçlardır. Bu sıradan karmaşık olanlardan bölünmüş karmaşık sayılar ayıran bu işareti değişimdir. Miktar j burada bir gerçek sayı değildir ancak bağımsız bir miktardır, bu ± 1'e eşit değildir.
Tüm bu z koleksiyonuna bölünmüş-karmaşık düzlem denir. Bölünmüş karmaşık sayıların Toplama ve çarpması aşağıdaki ile tanımlanır.
- (x + j y) + (u + j v) = (x + u) + j(y + v)
- (x + j y)(u + j v) = (xu + yv) + j(xv + yu).
Bu çarpma toplama üzerinde değişmeli, birleşimli ve dağılmalıdır.
Eşlenik, modül ve çift doğrusal form[değiştir | kaynağı değiştir]
Sadece karmaşık sayılar için, bölünmüş karmaşık eşlenik kavramını tanımlayabilirsiniz. Eğer
- z = x + j y
znin eşleniği olarak tanımlanır
- z∗ = x − j y.
Eşlenik olağan kompleks eşleniği ile benzer özelliklere taşır. Yani,
- (z + w)∗ = z∗ + w∗
- (zw)∗ = z∗w∗
- (z∗)∗ = z.
Bu üç özellik bölünmüş karmaşık eşleniğe işaret etmektedir sıra 2.nin bir otomorfizma'sıdır
Bir bölünmüş karmaşık sayının z = x + j y eşyönlü karesel form tarafından verilen modülü
önemli bir özelliği vardır, bu bölünmüş karmaşık çarpma tarafından korunmaktadır :
Bununla beraber, bu karesel form pozitif-tanım değildir ama oldukça yerine geçecek bir imza'sıdır (1, −1), bu modül bir norm değildir.
Birleşimli çifdoğrusal form ile verilir:
- 〈z, w〉 = Re(zw∗) = Re(z∗w) = xu − yv,
burada z = x + j y ve w = u + j v. modül için bir başka ifade ise
Pozitif-tanım olmadığından, bu çiftdoğrusal form bir iççarpım değildir; yine de çift doğrusal form sık sık bir belirsiz iç çarpım olarak adlandırılır. Dil kötüye benzer bir norm olarak modül ifade eder. Bölünmüş-karmaşık sayının tersi olan ancak ve ancak onun modül sıfırda farklı (). Bir ögenin çarpımsal ters aşağıdaki ile verilir
Split-karmaşık sayılar boş elemanların tersi değildir. Burada bütün (a ± j a) formunun bazı a gerçek sayıları içindir.
Köşegen taban[değiştir | kaynağı değiştir]
Burada iki önemsiz olmayan idempotent ile verilen e = (1 − j)/2 ve e∗ = (1 + j)/2. Bu idempotent demektir hatırlayın ee = e ve e∗e∗ = e∗. Bu öğelerin her ikisi de null(boş):
Sıklıkla kullanmak için e ve e∗ ye bir alternatif olarak bölünmüş karmaşık düzlemde tabandır . Bu taban köşegen taban veya null taban olarak adlandırılır,bölünmüş-karmaşık sayı z taban içinde aşağıdaki gibi yazılabilir.
- z = x + j y = (x − y)e + (x + y)e∗.
Eğer z = ae + be∗ sayısını göstermek istiyorsak gerçek sayılar a ve b ile (a, b), ise bölünmüş-karmaşık çarpma ile verilir
- (a1, b1)(a2, b2) = (a1a2, b1b2).
Bu baz olarak, toplama ve çarpma ile tanımlanan ikili R ⊕ R direkt toplamı izomorf halka'ya bölünmüş karmaşık sayılar için açıkça uyar.
köşegen bazında bölünmüş kompleks eşleniği aşağıdaki ile verilir
- (a, b)∗ = (b, a)
ve modülü aşağıdaki ile
Halkaların kategorisi aynı eşbiçimsel sınıfta uzanan olsa da Kartezyen düzlem içinde yerleşmiş kendi içinde farklı iki çizginin doğrudan toplamıdır. Bir düzlemsel haritalama olarak eşbiçimsel,,45 ° bir saat yönünün tersine bir √2 ile dönme oluşur vehiperbolik sektörü ile bağlantı bölgesinin içinde özellikle genleşme bazen karışıklığa neden olmuştur . gerçekten, hiperbolik açı içindeki sektörlerin bölge'ye karşılık gelen düzlemi ile bu "birim çember" aşağıda verilmiştir.
"birim çember" anlaşılır
bölünmüş karmaşık düzlemde karşılık gelen bir hiperbolik sektörün dilimi içinde sadece yarı alanında vardır. Bölünmüş karmaşık düzlem geometrisi de ayırt olmadığında böyle karışıklık sürdürülüyor olabilir.
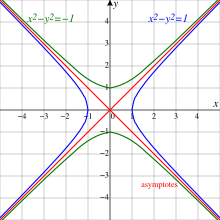
Geometri[değiştir | kaynağı değiştir]

eşlenik hiperbol ile ||z||=−1 (yeşil),
ve asimtotları ||z||=0 (kırmızı)
Minkowski iç çarpımı ile iki boyutlu gerçek vektör uzayı denen sıklıkla (1 + 1)-boyutlu ifade edilen Minkowski uzayıdır, R1,1 Öklid düzlemi R2 geometrisi gibi çok karmaşık numaraları ile tarif edilebilir, Minkowski'nin düzlemi,R1,1 geometrisi bölünmüş kompleks numaraları ile tarif edilebilir. Noktaların kümesidir
R içindeki a her sıfırdan farklı bir hiperbol bir sağ ve sol dalı (a, 0) ve (−a, 0) den geçerek oluşur. Durum a = 1 birim hiperbol denir. Eşlenik hiperbol ile verilir
Noktaları seti ile bir üst ve alt geçen dalı (0, a) ve (0, −a). Hiperbol ve eşlenik hiperbol boş elemanlarının kümesini oluşturan iki köşegen asimptot'lara ayrılır
Bu iki hat (bazen boş koni olarak adlandırılır)R2 içinde dik olan ve eğimli ± 1 var. bölünmüş-karmaşık sayılar z ve w ise hiperbolik-dik olduğu söylenmektedir Şablon:Dillez, wŞablon:Rangle = 0 dır. Sıradan diklik benzer olsa da, sıradan bir karmaşık sayı aritmetik ile bilinen özellikle de, bu durum daha güç algılanır. Bu uzay içinde aynı anda eşzamanlı hiperdüzlem kavramının temelini oluşturur. Bölünmüş karmaşık sayılar için Euler formülü analogu olan
Bu sinh için tek güçler varken cosh sadece çift güçler olduğu gerçeğini kullanarak bir güç seri açılımı elde edilebilir hiperbolik açısı için tüm gerçek değerleri için θ bölünmüş karmaşık sayıλ = exp(jθ) norm 1'e sahiptir ve birim hiperbol sağ kolu yatıyor. Bu λ gibi Numaraları hiperbolik versor'ler. olarak adlandırılabilir. λ tarafından çarpılan geometrik yapı korunur,.
Λ katsayısı 1, sahip olduğu herhangi bir λ ile herhangi bir bölünmüş karmaşık sayı z çarparak z ve modülü korunur ve bir hiperbolik dönme alarak, geometrik yapısını korur, kendilerini ve kendisi için boş koni hiperbolas alarak (bir Lorentz boost veya bir sıkı haritalama gibi adlandırılır). Modülü (veya eşdeğer, iç çarpım) genelleştirilmiş dik grup O(1, 1) adlı bir grup oluşturan korumak bölünmüş karmaşık düzlemde tüm dönüşümlerin kümesi Bir alt grup SO+(1, 1) formu tarafından verilen dört ayrık yansımaları ile birlikte bu grup hiperbolik dönme oluşturur
- ve
Üstel harita
exp(jθ) tarafından θ ya gönderilen bir eşbiçim grup ile kullanılan üstel formül uygulaması:
Eğer bir çift-karmaşık sayı z köşegenin bir yatık şekli değil, ise z bir kutupsal ayrışma'dır.
Matris gösterimleri[değiştir | kaynağı değiştir]
Bölünmüş-karmaşık sayılar
- z = x + j y
matrisler'i tarafından kolayca gösterilebilir
bölünmüş-karmaşık sayıların toplama ve çarpımı toplama ve çarpım matrisleri tarafından verilebilir.znin modülü mukabil matrisin determinantı tarafından verilir.Bu gösterim içinde,iki yüz olarak bölünmüş-karmaşık eşlenik matris tarafından çarparak karşılık gelir
herhangi bir gerçek sayı a,bir hiperbolik açı tarafından hiperbolik rotasyon a çarpımına karşılık gelen matris ile

Bölünmüş karmaşık sayı düzlemi diagonal bazında için sıralı bir (x, y) çifti kullanılarak çağrılabilir ve haritalama yapıyor
Şimdi ikinci dereceden formu dir Ayrıca,
böylece iki parametrize hiperboller Sile karşıkarşıya getirilir. hiperbolik versor 'nın hareket ise bir sıkarak haritalama'nın doğrusal dönüşümü altında karşılık gelen
Burada 2 × 2 gerçek matris'in konusunu bu bağlamda unutmayın Aslında bölünmüş kompleks sayıların farklı temsillerinin büyük bir sayıdadır. Jordan kurallı formu bölünmüş karmaşık sayının matris gösterimini yukarıdaki köşegen gösterim temsil etmektedir. Bölünmüş-karmaşık sayılar aşağıdaki matris gösterimi için z = (x, y) tarafından verilir:
Bu Jordan kurallı formu ile verilen:
burada ve
Tarihçe[değiştir | kaynağı değiştir]
Bölünmüş karmaşık sayılar kullanılması 1848 uzanır James Cockle Tessarine'yı ortaya çıkardı.William Kingdon Clifford spinlerin toplamını gösteren temsil bölünmüş karmaşık sayılar kullanır . Clifford şimdi bölünmüş-çiftdördeyler adı verilen bir kuaterniyon cebir katsayıları olarak bölünmüş-karmaşık sayılar kullanımı tanıttı . O ögelere "motorlar" dendi,daire grup'tan alınan sıradan bir karmaşık sayının "rotor" eylemine paralel bir terimle çağrıldı. Benzerlik sıradan bir karmaşık değişkenli fonksiyonlar için bir motor değişken kontrast fonksiyonlarına uzatılabilir . Yirminci yüzyıldan beri,bölünmüş-karmaşık çarpma yaygın bir uzayzaman - planının bir Lorentz boost'a destek olarak görülmüştür . Bu modelde, sayı z = x + y j Mermin ayakları içindeki y nanosaniye içindeki x burada ve y ölçülür bir uzay-zamansal planda, bir olay temsil eder. Gelecekteki olayların kadrandaki karşılığı {z : İfade hatası: Tanınmayan "'" noktalama karakteri.<x}, bölünmüş karmaşık polar ayrışma sahip olduğu . Model z a hızla bir referans çerçevesi'ne girerken ve ρ nanosaniye bekleyerek orijine ulaşılabileceğini söylüyor . Bölünmüş karmaşık denklemi
birim hiperbol üzerinde çarpım ifadesi doğrudaş hızları için hızların toplanırlığını göstermektedir . Olayların eşzamanlılık hız a 'ya bağlıdır ;
a hızlı referans çerçevesinde orijin eşzamanlı olayların hattıdır. Iki olay z ve w hiperbolik-dik olduğunda z∗w + zw∗ = 0. Kanonik olaylar exp(aj) vej exp(aj) orijini ile eşzamanlı olayları j exp(aj) ile orantılı olduğu referans çerçevesinin eksende dik hiperbolik ve Lie'dir . 1.935 J.C. Vignaux ve A.Durañona y Vedia Contribución bir las Ciencias Físicas y Matemáticas, National University of La Plata, República Argentina (in Spanish) dört makalelerde bölünmüş Geometrik cebir ve fonksiyonlar teorisi geliştirdi. Bu açıklayıcı ve pedagojik denemeleri geniş takdir için konu sundu.
1941 yılında EF Allen zz∗ = 1 içinde yazılı bir üçgenin dokuz-nokta bir hiperbol kurmak için bölünmüş Geometrik aritmetik kullanılır .
1956 yılında Mieczyslaw Warmus Bulletin de l’Academie Polanaise des Sciences te "Yaklaşıklıklar Hesabı" (Referanslar bağlantıya bakınız) yayınladı. O bölünmüş karmaşık sayı ile bir aralık [a, A] tespit
- ve bir "yaklaşık sayı" olarak nitelendirdi. D. H. Lehmer Matematiksel Yorumlar Mathematical Reviews..
1961 yılında Warmus aralığının orta noktası ve yarıçapı ifade olarak yaklaşık sayıda bileşenleri atıfta bulunarak, onun fuar devam etti.
Eşanlamlılar[değiştir | kaynağı değiştir]
Farklı otörler çift-kompleks sayılar için isimlerin büyük bir çeşitliliğini kullandı. Bunlardan bazıları şunlardır:
- (gerçek) tessarines, James Cockle (1848)
- (cebrik) motorlar, W.K. Clifford (1882)
- hiperbolik kompleks sayılar, J.C. Vignaux (1935)
- çiftgerçek sayılar, U. Bencivenga (1946)
- yaklaşık sayılar, Warmus (1956), for use in interval analysis
- countercomplex veya hyperbolic numbers from Musean hypernumbers
- ikikat sayılar, I.M. Yaglom (1968) and Hazewinkel (1990)
- anormal-kompleks sayılar, W. Benz (1973)
- kafakarıştırıcı sayılar, P. Fjelstad (1986) and Poodiack & LeClair (2009)
- Lorentz sayıları, F.R. Harvey (1990)
- hiperbolik sayılar, G. Sobczyk (1995)
- yarı-karmaşık sayılar, F. Antonuccio (1994)
- bölünmüş-karmaşık sayılar, B. Rosenfeld (1997)
- uzayzaman sayıları, N. Borota (2000)
- ikizkarmaşık sayılar, S. Olariu (2002)
Bölünmüş-karmaşık sayılar ve yüksek-boyutlu ilişkiler (bölünmüş-dördey'ler / eşdördeyler ve bölünmüş -sekizeylerler) zaman zaman "Musean Sayılar" olarak adlandırılmıştır, öyle ki Charles Musès'in geliştirdiği aşkınsayılar'ın bir alt kümesidir.
Ayrıca bakınız[değiştir | kaynağı değiştir]
Bir modifiye ile elde edilen bölünmüş karmaşık sayılar daha yüksek mertebeden türevler, Cayley-Dickson yapısı:
- bölünmüş-Dördey (veya eş-dördey)
- bölünmüş-sekizey
Lie Teorik olarak, daha soyut bir genelleme oluşur:
Cebir ve sayılar programları zarfı:
Kaynaklar ve Dış bağlantılar[değiştir | kaynağı değiştir]
- Francesco Antonuccio (1994) Semi-complex analysis and mathematical physics22 Ağustos 2016 tarihinde Wayback Machine sitesinde arşivlendi.
- Bencivenga, Uldrico (1946) "Sulla rappresentazione geometrica della algebra doppie dotate di modulo", Atti della real academie della scienze e belle-lettre di Napoli, Ser (3) v.2 No7. MR0021123.
- Benz, W. (1973)Vorlesungen uber Geometrie der Algebren, Springer
- N. A. Borota, E. Flores, and T. J. Osler (2000) "Spacetime numbers the easy way", Mathematics and Computer Education 34: 159-168.
- N. A. Borota and T. J. Osler (2002) "Functions of a spacetime variable", Mathematics and Computer Education 36: 231-239.
- K. Carmody, (1988) "Circular and hyperbolic quaternions, octonions, and sedenions", Appl. Math. Comput. 28:47–72.
- K. Carmody, (1997) "Circular and hyperbolic quaternions, octonions, and sedenions – further results", Appl. Math. Comput. 84:27–48.
- F. Catoni, D. Boccaletti, R. Cannata, V. Catoni, E. Nichelatti, P. Zampetti. (2008) The Mathematics of Minkowski Space-Time, Birkhäuser Verlag, Basel. Chapter 4: Trigonometry in the Minkowski plane. ISBN 978-3-7643-8613-9.
- Cockle, James (1848) "A New Imaginary in Algebra", London-Edinburgh-Dublin Philosophical Magazine (3) 33:435–9.
- Clifford, W.K.,Mathematical Works (1882) edited by A.W.Tucker,pp. 392,"Further Notes on Biquaternions"
- De Boer, R. (1987) "An also known as list for perplex numbers", American Journal of Physics 55(4):296.
- Fjelstadt, P. (1986) "Extending Special Relativity with Perplex Numbers", American Journal of Physics 54:416.
- F. Reese Harvey. Spinors and calibrations. Academic Press, San Diego. 1990. ISBN 0-12-329650-1. Contains a description of normed algebras in indefinite signature, including the Lorentz numbers.
- Hazewinkle, M. (1994) "Double and dual numbers", Encyclopaedia of Mathematics, Soviet/AMS/Kluwer, Dordrect.
- Louis Kauffman (1985) "Transformations in Special Relativity", International Journal of Theoretical Physics 24:223–36.
- C. Musès, "Applied hypernumbers: Computational concepts", Appl. Math. Comput. 3 (1977) 211–226.
- C. Musès, "Hypernumbers II—Further concepts and computational applications", Appl. Math. Comput. 4 (1978) 45–66.
- Olariu, Silviu (2002) Complex Numbers in N Dimensions, Chapter 1: Hyperbolic Complex Numbers in Two Dimensions, pages 1–16, North-Holland Mathematics Studies #190, Elsevier ISBN 0-444-51123-7.
- Poodiack, Robert D. & Kevin J. LeClair (2009) "Fundamental theorems of algebra for the perplexes", The College Mathematics Journal 40(5):322–35.
- Rosenfeld, B. (1997) Geometry of Lie Groups Kluwer Academic Pub.
- Sobczyk, G.(1995) Hyperbolic Number Plane13 Kasım 2013 tarihinde Wayback Machine sitesinde arşivlendi., also published in College Mathematics Journal 26:268–80.
- Vignaux, J.(1935) "Sobre el numero complejo hiperbolico y su relacion con la geometria de Borel", Contribucion al Estudio de las Ciencias Fisicas y Matematicas, Universidad Nacional de la Plata, Republica Argentina.
- M. Warmus (1956) "Calculus of Approximations"9 Mart 2012 tarihinde Wayback Machine sitesinde arşivlendi., Bulletin de l'Academie Polonaise de Sciences, Vol. 4, No. 5, pp. 253–257;
- Yaglom, I. (1968) Complex Numbers in Geometry, translated by E. Primrose from 1963 Russian original, Academic Press, N.Y., pp. 18–20.





![{\displaystyle \mathbb {R} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16d740527b0b7f949b4bf9c9ce004134bb490b68)


![{\displaystyle \mathbb {R} [X]/(X^{2}-1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4586f3aa300d4caf954605ade10ae0807223050)
















































