Normal dağılım
| İstatistik dizisinin bir parçası |
| Olasılık teorisi |
|---|
 |
Olasılık yoğunluk fonksiyonu Standard normal dağılım yeşil çizgi ile gösterilir | |
Yığmalı dağılım fonksiyonu Renkler yukarıdaki gösterim ile aynıdır | |
| Parametreler | konum (reel) kare ölçek (reel) |
|---|---|
| Destek | |
| Olasılık yoğunluk fonksiyonu (OYF) | |
| Birikimli dağılım fonksiyonu (YDF) | |
| Ortalama | |
| Medyan | |
| Mod | |
| Varyans | |
| Çarpıklık | 0 |
| Fazladan basıklık | 0 |
| Entropi | |
| Moment üreten fonksiyon (mf) | |
| Karakteristik fonksiyon | |
Normal dağılım, aynı zamanda Gauss dağılımı veya Gauss tipi dağılım olarak isimlendirilen, birçok alanda pratik uygulaması olan, çok önemli bir sürekli olasılık dağılım ailesidir.
Bu dağılım ailesinin her bir üyesi sadece iki parametreyle tam olarak tanımlanabilir: Bunlar konum gösteren ortalama (μ, aritmetik ortalama) ve ölçek gösteren varyans (σ2, "yayılım")dır.
Standart normal dağılım, ortalama değeri 0 ve varyans değeri 1 olan normal dağılım ailesinin tek bir elemanıdır. Carl Friedrich Gauss bu dağılımlar grubu ile, astronomik verileri analiz etmekte iken, ilgilenmiş ve bu dağılım için olasılık yoğunluk fonksiyonunu ilk defa tanımlamıştır.[1] Bu olasılık fonksiyonunun grafiği, bir çana benzediği için çoğu kez çan eğrisi olarak da anılmaktadır.
Doğa ve davranış bilimleri içinde bulunan birçok fenomenin niceliksel modeli yapılmasında normal dağılımın kullanılmasına neden merkezsel limit teoreminin uygulanmasından doğmaktadır. Birçok psikolojik ölçümler ve fiziksel fenomen normal dağılım kullanılarak çok iyi yaklaşık olarak açıklanmaktadır. Bu fenomenlerin altında yatan mekanizmalar çoğu zaman bilinmemekte fakat normal dağılım modelinin açıklamada uygulanmaktadır. Bunun pratik yaklaşımın teorik olarak savunması ise her bir reel gözlemin oluşması için geri planda çok sayıda birbirinden bağımsız etkilerin ayrı ayrı toplam olarak katkıda bulundukları varsayımıdır.
Normal dağılım istatistik biliminin birçok alanında kullanılmaktadır. Örneğin örneklem ortalaması için örnek dağılımı, örneğin kaynağı olan anakütle için dağılımın normal olmadığı gayet açık olsa bile, yaklaşık olarak normal dağılım göstermektedir. Bunun yanında, değerleri bilinen ortalaması ve varyansı olan bütün dağılımlar içinde enformasyon entropisini maksimum yapan dağılımın normal olduğu ispat edilmiştir. Böylece örnek ortalaması ve varyansı ile özetlenen her veri için bilinmeyen kaynak dağılımı olarak normal dağılımı kullanmak gayet doğal bir yaklaşım olması çok uygun bir davranıştır. İstatistikte kullanılan dağılımlar aileleri arasında normal dağılım pratikte en çok kullanılanıdır ve birçok istatistiksel test, normal dağılımın varolduğu varsayımına dayanılarak geliştirilmiştir ve kullanılmaktadır. Olasılık kuramı içinde birkaç sürekli olasılık dağılımları ve ayrık olasılık dağılımlarının limite giden dağılımları yani rassal değişkenlerin yakınsama analizinde kullanılmaktadır.
Tarihçe[değiştir | kaynağı değiştir]
İstatistik ve olasılığın önemli dağılımlarından biri olan normal dağılım, ilk olarak 1733'te Abraham de Moivre tarafından yayınlanan bir yazıda ilk ortaya çıkartılmıştır ve 1738'de yayınlanan The Doctrine of Chances (Şanslar Doktrini) adlı kitabının ikinci baskısında p değişmemek koşuluyla n değerinin artısıyla binom dağılımının limit şekli yaklaşım olarak gösterilmiştir. De Moivre'in bu sonucu Laplace tarafından 1812'de bastırılan Analytical Theory of Probabilities (Olasılıklar İçin Analitik Teori) geliştirilmiştir ve bu sonuç şimdi de Moivre-Laplace teoremi olarak isimlendirilmektedir.
Laplace normal dağılımı incelemekte olduğu deneylemelerde hataların analizi konusunda uygulamıştır. 1805'te Legendre çok önemli olan en küçük kareler yöntemini ortaya atmıştır. Gauss, bu yöntemi1794'ten beri kullandığını iddia etmiştir ama en kesin surette hataların normal dağılımı varsayımı ile birlikte yayınladığı eser 1809'dadır.
Çan eğrisi teriminin ilk kullanılışı Jouffret tarafından 1875'te bir bağımsız parçalardan oluşan ikideğişirli normal hakkında yazıda çan yüzeyi teriminin kullanmasına kadar götürülebilir. Normal dağılım sözcüğü iseCharles S. Peirce, Francis Galton ve Wilhelm Lexis tarafından ayrı ayrı 1875 civarlarında ortaya atılmıştır.
Bu dağılıma normal adı vermek bazen hatalı görülmektedir; çünkü bazı hallerde diğer dağılımlar pratiğe çok daha uygunluk göstermektedirler.
Karakteristikler[değiştir | kaynağı değiştir]
Bir olasılık dağılımını çeşitli şekilde matematiksel ifadelerle karakterize etmek mümkündür. Bunlar arasında göze en iyi hitap edeni olasılık yoğunluk fonksiyonu ile olur. Dağılımın özellikleri ayrıca birikimli dağılım fonksiyonu,momentler, kümülantlar, karakteristik fonksiyon, moment üreten fonksiyon, kümülant üreten fonksiyon ve Maxwell'in teoremi vasıtasıyla da belirtilebilir. Bu kavramların ayrıntıları için olasılık dağılımları maddesine bakınız.
Matematiksel notasyon kullanılması ile, X rassal değeri için ortalama değeri μ ve varyansı σ² ≥ 0, olan bir normal dağılımın bulunduğu şöyle ifade edilir:
Normal dağılım için fazla kullanılmayan bir değişik parametreleme şekli de bulunmaktadır. Bu (bir üssü varyans yani 1/ σ²), değerine eşit olan kesinlik parametresi τ kullanılarak yapılır. Bunun avantajı sıfır değerine çok yakın varyans (σ²) değerlerinin böler olmalarından doğan limit problemlerinden ayrılma imkânı sağlaması ve normal dağılımı bir üstel ailesi bireyi olarak kullanılması gerektiği halde ortaya çıkar.
Bazı merkezsel limit teoremleri için (örneğin kestirimlerin asimtotik normalliği) Gauss tipi süreçler teorisi kullanışlı olmakla beraber, tüm olasılığı μ etrafında konsantre eden ve bir normal dağılıma benzer olarak ortalama μ ve varyans σ² = 0 değerleri bulunan Dirac ölçümü bir normal dağılım olarak kabul edilmemektedir; buna matematiksel açıklama bu ölçümde Lebesque ölçümü kurallarına göre gereken yoğunluğun bulunmamasıdır.
Olasılık yoğunluk fonksiyonu[değiştir | kaynağı değiştir]

Normal dağılım için sürekli olasılık yoğunluk fonksiyonu şu Gauss-tipi fonksiyondur:
Burada σ > 0 standart sapmadır; bir reel parametre olan μ beklenen değerdir; ve
ifadesi standart normal dağılım için yoğunluk fonksiyonudur. Standart normal dağılım μ = 0 ve σ = 1 parametreleri olan bir normal dağılımdır.
ifadesinin reel doğru üzerindeki integral değeridir. (Ayrıntıları için Gauss-tipi entegral maddesine bakınız.)
Olasılık yoğunluk fonksiyonunun özellikleri arasında şunlar başta gelenlerdir:
- ortalama değer μ etrafında simetrik olma;
- hem modun hem de medyanın ortalama μ değerine eşit olması;
- yoğunluk eğrisinin üzerindeki, ortalamadan birer standart sapma altında ve üstündeki noktalar arasında (yani μ - σ ve μ+σ noktalarında) bir ''enfleksyon'' noktası bulunması.
Birikimli dağılım fonksiyonu[değiştir | kaynağı değiştir]

Bir olasılık dağılımı için birikimli dağılım fonksiyonu, bir rassal değişken X için olay olasılığının dağılımının x sayısına eşit veya daha düşük olmasına kadar değerlendirilmesinden ortaya çıkar. Normal dağılım için birikimli dağılım fonksiyonu (yoğunluk fonksiyonunda kullanılan ayn terimlerle) şöyle ifade edilir:
Burada, parametreleri μ = 0 ve σ = 1 olan standart normal dağılımı için birikimli dağılım fonksiyonu, Φ, ile ifade edilmiştir ve bu fonksiyon şudur:
Standart normal birikimli dağılım fonksiyonu aynı zamanda hata fonksiyonu adı verilen bir özel fonksiyon ifade edilebilir. Hata fonksiyonu şöyle ifade edilir:
Böylece hata fonksiyonu terimleri ile standart normal dağılımı için birikimli dağılım fonksiyonu şöyle yazılır:
Standart normal dağılım için birikimli dağılım fonksiyonunun tamlayıcı fonksiyonu (yani ), çok kere Q-fonksiyonu olarak isimlendirilir ve özellikle bu kavram mühendislik kitaplarında büyük önemle yer almaktadır.
Standart normal birikimli dağılım fonksiyonunun tersine kuantil fonksiyonu adı verilir. Bunun formülünü ifade için önce şu ters hata fonksiyonu bulunur:
ve bu fonksiyon kullanılarak şu ters birikimli dağılım fonksiyonu ortaya çıkartılır:
Bu kuantil fonksiyonuna bazen probit fonksiyonu adı da verilir. Bir probit fonksiyonu için bir elemanter basit entegralbulunamayacağı matematiksel olarak ispat edilmiştir. Normal dağılım için çok iyi sonuçlar verdiği anlaşılan yaklaşık fonksiyonlar ve yöntemler ortaya çıkarılmıştır. Bunlar arasında sayısal entegrasyon, Taylor serileri, asimtotik seriler vedevam eden kesirler yöntemlerinin kullanılması anılabilir.
Birikimli dağılım fonksiyonu için kesin alt ve üst sınırlar[değiştir | kaynağı değiştir]
Büyük değerde bir x sayısı için standart normal dağılım birikimli dağılım fonksiyonun değerinin bire,1, yakınsalandığı ve ın ise sıfıra,0, yakınsaladığı aşikardır. Yoğunluk terimleri kullanılarak, şu basit üst sınır
ifadesi yeterlidir.
Yerine koymak suretiyle entegresyon yöntemi kullanarak, üst sınır şöyle ortaya çıkartılabilir:
Aynı şekilde ifadesini ve bölüm kuralını kullanarak
ifadesi ortaya çıkartılır. Bunun terimleri ile çözümlenmesi yukarıda ifade edilen üst sınırı verir.
Üreten fonksiyonlar[değiştir | kaynağı değiştir]
Moment üreten fonksiyon[değiştir | kaynağı değiştir]
Genel olarak moment üreten fonksiyon, exp(tX) için beklenen değer olarak tanımlanır. Bir normal dağılım için moment üreten fonksiyonu şu olur:
Bu ifade, tanımda verilen üssel değerin, karesini tamamlamak yöntemi dönüştürülmesi ile elde edilmiştir.
Kümülant üreten fonksiyon[değiştir | kaynağı değiştir]
Kümülant üreten fonksiyon, moment üreten fonksiyonun logaritmasidir:
- g(t) = μt + σ²t²/2.
Bu t terimleri ile bir kuadratik polinom olduğu için yalnız ilk iki kümülant için sıfır olmayan değer bulunabilinir.
Karakteristik fonksiyon[değiştir | kaynağı değiştir]
Karakteristik fonksiyon, sanal birim ile gösterilen ifadesinin beklenen değersi olarak tanımlanmıştır. Bu nedenle karakteristik fonksiyon, moment üreten fonksiyon içindeki teriminin ile değiştirilmesi ile elde edilir.
Bir normal dağılımı için karakteristik fonksiyonu şudur:
Özellikleri[değiştir | kaynağı değiştir]
Normal dağılımın şu özellikleri vardır:
- Eğer ve ile reel sayılar ise, o zaman (Beklenen değer ve varyans maddelerine bakınız.).
- Eğer ve ifadeleri bağımsız normal rassal değişkenler ise, o halde -
- Bunların toplamı normal dağılım gösterir (proof). Daha ilgi çekici olarak bunun tersi de geçerlidir: Eğer iki bağımsız rassal değişkenlerin toplamı normal dağılım gösteriyorsa, her iki değişken de ayrı ayrı normal dağılım gösterirler. Bu Cramer'in teoremi olarak isimlendirilmiştir.
- Bunların arasındaki fark şu şekilde normal dağılım gösterir: Yani .
- Eğer X ve Y rassal değişkenlerinin varyansları birbirine eşitse, U (toplam için rassal değişken) ve V (fark için rassal değişken) birbirinden bağımsızdırlar.
- Kullback-Leibler ayrımı şöyle ifade edilir
- Eğer ve birbirinden bağımsız normal rassal değişkenler ise; o zaman
- Bunların çarpımı, yani , ile şöyle ifade edilen yoğunluk fonksiyonu olan özel bir dağılım gösterir
- Bunların birbirine oranı şekilde Cauchy dağılımı gösterir. Böylece bu Cauchy dağılımı özel bir tip orantı dağılımı olur.
- Eğer bir seri bağımsız standart normal değişkenler ise, o zaman bunların toplamı, yani n serbestlik dereceli bir ki-kare dağılımı gösterir.
Normal rassal değişkenlerin standart forma dönüşümleri[değiştir | kaynağı değiştir]
Yukarıda verilen 1. özellik sonucu olarak tüm normal rassal değişkenleri standart normale dönüştürmek imkânı vardır: Eğer ~ ise, bu halde
bir standart normal rassal değişken olur; yani ~ .
Bunun bir önemli sonucu birikimli olasılık fonksiyonun bir genel normal dağılımı olmasıdır:
Tersini ele alırsak, eğer bir standart normal dağılım ise, yani ~ ise o halde
ifadesi de beklenen değeri ve varyansı olan bir normal rassal değişkendir.
Standart normal dağılım için çeşitli tablolar bulunmaktadır. Çok kere bu tablolar birikimli dağılım fonksiyonu, Φ şeklindedirler. Diğer normal dağılımlar basit bir dönüşüm ile standart normal dağılıma dönüştürülüp bu tablolardan biri kullanılabilir.
Momentler[değiştir | kaynağı değiştir]
Normal dağılım için ilk birkaç momentleri şunlardır:
| Sayı | Ham moment | Merkezsel moment | Kümülant |
|---|---|---|---|
| 0 | 1 | 1 | |
| 1 | 0 | ||
| 2 | |||
| 3 | 0 | 0 | |
| 4 | 0 | ||
| 5 | 0 | 0 | |
| 6 | 0 | ||
| 7 | 0 | 0 | |
| 8 | 0 |
Normal dağılım için ilk iki kümülant dışındaki kümülant değerler hep sıfıra eşittir.
Daha büyük sayıya bağlı ( derecede ve ) merkezsel momenti şu formül kullanılarak elde edilebilir:
Normal rassal değişirler için üretici değerler[değiştir | kaynağı değiştir]
Bilgisayarla simulasyon yapılmakta iken, çok kere bir normal dağılım için değerlerin üretilmesi gerekir. Bunun için birkaç değişik yöntem kullanılabilir. En basit şekilde bir standart normal dağılım birikimli olasılık fonksiyonunun tersini almak suretiyle elde edilir. Daha etkin yöntemler de geliştirilmiştir.
Çok popüler olarak kullanılan yöntem Box-Muller dönüşümüdür. Box-Muller algoritması kullanılması, [0,1] arasında bulunan sürekli tekdüze dağılım gösteren iki sayı a ve b ile başlar; bunlardan şu formüllere göre iki standart normal dağılım gösteren c ve d sayıları şöyle elde edilir:
Bunların elde edilmesi, dönüşümün bazında (yukarıda 4. özellikte gösterilen) 2 serbestlik derecesi olan bir ki-kare dağılımının kolayca üretilebilinen bir üstel rassal değişken olması gerçeğine dayandırılır.
Halen en etkin şekilde normal dağılımı simulasyonu için, ziggurat algoritması kullanılmaktadır.
Merkezi limit teoremi[değiştir | kaynağı değiştir]

Sonlu varyansları olan bağımsız ve aynı dağılımlı rassal değişkenler ve benzeri koşullar altında, büyük sayıda rassal değişkenlerin toplamı yaklaşık olarak normal dağılım gösterir. Bu merkezsel limit teoremidir.
Merkezsel limit teoreminin pratik önemi normal birikimli dağılım fonksiyonunun bazı diğer birikimli dağılım fonksiyonunun yaklaşık olarak kullanabilmesindedir. Örneğin
- Parametreleri n ve p olan bir binom dağılım için, eğer büyük değerlerde, ama 0 veya 1e çok yakın olmayan n vep bulunursa bir normal dağılımına yaklaşmış oldukları kabul edilebilir. (Bazı istatistik kitapları bu yaklaşımın np ve n(1 -p değerlerinin her ikisi için en aşağı 5 olması halinde uygulanmasını ve eğer 5 olurlarsa bir devamlılık doğrulaması kullanılmasını tavsiye ederler.)
Eğer yaklaşık olarak normal dağılımı kullanılırsa bunun parametreleri μ = np ve σ2 = np(1-p) olarak bulunması gerekir. - Eğer λ'nin değeri büyük ise, λ parametreli Poisson dağılımı için yaklaşık olarak normal dağılım kullanılabilir ve bu halde yaklaşık normal dağılımın parametreleri μ = σ2 = λ olarak bulunur.
Bu yaklaşımların yeter derecede doğru olup olmayacağı, sonuçların ne maksatlarla kullanacaklarına ve normal dağılımın yakınsalama oranına bağlıdır. Bu tip yaklaşımlar dağılımın kuyruk değerlerine yaklaştıkça gittikçe daha çok hatalı olacaklardır. Berry-Essen teoremi birikimli dağılım fonksiyonu için yaklaşım hatası için genel üst sınırları gösterir.
Sonsuz olarak bölünebilme[değiştir | kaynağı değiştir]
Normal dağılımlar sonsuz olarak bölünebilen olasılık dağılımlarıdır: Bir ortalama değeri μ, bir varyans değeri σ2≥ 0 ve bir doğal sayı değeri n verildiği zaman, n bağımsız rassal değişkenlerin toplamı olan 'X1 + . . . +Xn' şu normal dağılımı gösterir:
- ç
(Daha fazla ayrıntı için matematik tümevarım ile normal dağılım gösteren rassal değişkenlerin toplamı maddelerine bakınız.)
Dengelilik[değiştir | kaynağı değiştir]
Normal dağılımlar kesinlikle dengelilik gösteren olasılık dağılımlarıdır.
Standart sapma ve güven aralıkları (açıklıkları)[değiştir | kaynağı değiştir]
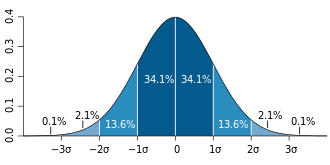
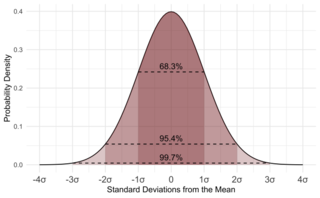
Bir normal dağılımdan seçilmiş değerlerin %68i ortalama olan μ'in bir standart sapma σ > 0 uzaklığındaki noktalar arasındadır; değerlerin neredeyse %95i μ'den iki standart sapma uzaklıklar aralığında; ve %99,7 üç standart sapma uzaklıklar aralığında bulunur. Buna empirik kural veya 68-95-99.7 kuralı adı da verilir.
Daha doğru bir kesin ifadeyle μ - nσ ve μ + nσ arasındaki çan eğrisinin altında kalan alanın birikimli normal dağılım fonksiyonu şöyle verilir:
Burada erf hata fonsiyonudur. Ondalık sayılarla 12 basamak kullanılarak 1-, 2- .. 6- sigma noktalarına kadar değerler şöyle verilir:
| 1 | 0.682689492137 |
| 2 | 0.954499736104 |
| 3 | 0.997300203937 |
| 4 | 0.999936657516 |
| 5 | 0.999999426697 |
| 6 | 0.999999998027 |
İkinci tablo çan eğrisinin altındaki alan için değerlerin bulunmasını sağlamak üzere, çok zaman kullanılan katsayı değerlerindeki, sigma çarpanlarının ters ilişkisini gösterir. Normal dağılım gösteren veya asimtotda normal olan kestirimler için belirtilmiş olan seviyelerde (asimtotik) güvenlik aralığını saptamak için bu değerler çok kullanışlıdır:
| 0.80 | 1.28155 |
| 0.90 | 1.64485 |
| 0.95 | 1.95996 |
| 0.98 | 2.32635 |
| 0.99 | 2.57583 |
| 0.995 | 2.80703 |
| 0.998 | 3.09023 |
| 0.999 | 3.29052 |
Bu tabloda sol taraftaki sütun bilinen bir aralığa düşecek değerlerin oranı verilmekte ve soldaki n sütunu ise aralığın genişliğinin kaç tane standart sapma birimini ihtiva ettiğini göstermektedir.
Üstel ailesi şekli[değiştir | kaynağı değiştir]
Normal dağılım bir iki parametreli üstel ailesi elemanıdır. İki tane doğal parametresi μ ve 1/σ2 olur ve doğal istatistikleri X ve X2 dir. Kanonik şeklinin parametreleri ve olup yeterli istatistikleri ve olur.
İlişkili dağılımlar[değiştir | kaynağı değiştir]
- Eğer ise ve burada ave iki bağımsız normal dağılımlarsa, o halde bir Rayleigh dağılımı olur.
- Eğer ise ve burada için ise ve bunların hepsi bağımsızlarsa; o zaman serbestlik derecesi olan bir ki-kare dağılımıolur.
- Eğer iki bağımsız normal dağılımlı ve
için ise, o zaman bir Cauchy dağılımıdır.
- Eğer ve ise, o zamanbirlog-normal dağılımıdır.
- Lévy çarpık alpha-durağan dağılımına ilişki : Eğer ise o halde .
- Kesilmiş normal dağılımı. Eğer o halde Xi alttan 'da ve üstten'de kesmek suretiyle, ortalaması olan bir rassal değişken ortaya çıkarılır.
Burada olur ve bir standart normal rassal değişken için bir olasılık yoğunluk fonksiyonu olur.
- Eğer normal dağılım gösteren bir rassal değişken ise ve ise, o halde bir katlanmış normal dağılım gösterir.
Betimsel ve çıkarımsal istatistikler[değiştir | kaynağı değiştir]
Puanlar[değiştir | kaynağı değiştir]
Puan verme çeşitlerinin çoğu normal dağılıma bağlı olarak ortaya çıkarılmıştır. Değişik puanlama yöntemleri arasında yüzbirliklerle sıralamalar, normal eğri eşitliklikleri, staninler, z puanı ve T-puanlaması vb. sayılabilir. Davranışsal bilimlerde kullanılan birçok istatistiksel yordamlar puanların normal dağılım gösterdiği varsayımına dayanılarak geliştirilmiştir. Örneğin çok kişiye uygulanan imtihan veya zeka testleri için bir çan eğrisine dayanan not verilip imtihan veya test sonuçlarının gruplanması veya sıralanması imtihan veya test notlarının normal dağılım gösterdiği varsayımına dayandırılır.
Normallik sınamaları[değiştir | kaynağı değiştir]
Normallik sınamaları, verilmiş bir veri dizisinin normal dağılıma benzerliğinin incelenmesidir. Bu sınamalarda sıfır hipoztez veri dizisinin normal dağılıma benzer olmasıdır. Bu nedenle normal olmayan veri için yeter derecede küçük bir p-değeri (yani genellikle %0,05'ten veya 0,01den küçük) ortaya çıkacak ve sıfır hipotez olan veri dizisinin normal dağılıma benzerliği hipotezinin ret edilmesine neden olacaktır.
- Kolmogorov-Smirnov sınaması
- Lilliefors sınaması
- Anderson-Darling sınaması
- Ryan-Joiner sınaması
- Shapiro-Wilk sınaması
- Normal olasılık gösterimi (rankit gösterimi)
- Jarque-Bera sınaması
Parametrelerin kestirimi[değiştir | kaynağı değiştir]
Parametrelerin maksimum olabilirlik kestirimi[değiştir | kaynağı değiştir]
Bir düşünce denemesi olarak, bir seri normal dağılım için
ifadesinin her biri diğerinden bağımsız olduğu düşünülsün. Her bir ifade beklenen değersi μ ve varyansı σ2>0 olan normal dağılımlar göstermektedir. İstatistikçiler bu n rassal değişkenin gözümlenen değerlerinin normal dağılım gösteren bir anakütleden ortaya çıkan bir n büyüklüğünde bir örneklem olduğunu kabul etmektedirler. Bu örneklemden gözlenen değerlere dayanarak "anakütle ortalaması" μ ve "anakütle standart sapması" kestirimcilerini bulmak arzu edilmektedir. Bu n sayıdaki bağımsız rassal değişken için sürekli ortak olasılık yoğunluk fonksiyonu şöyle verilir:
μ ve σ fonksiyonları olarak, X1, ..., Xn gözlemlerine dayanan olabilirlik fonksiyonu şudur:
Burada C>0 herhangi bir sabittir. Bunun genellikle X1,...,Xn değişkenlerine bile dayanarak bağlandığı kabul edilmektedir; ama hesaplanan parametrelere göre log-olabilirlik fonksiyonların kısmî türevleri bulunduğu zaman sabit oldukları için elimine edilmektedirler.
Maksimum olabilirlik yöntemine göre olabilirlik fonksiyonu maksimize eden μ ve σ değerleri, teorik anakütle parametreleri olan μ ve σ için kestirim oldukları kabul edilmektedir. Genel olarak iki değişkenli bir fonksiyonun maksimum değerini hesaplanmaktayken kısmî türevler kullanılır. Ancak burada maksimum hesaplama daha kolaylaşmaktadır çünkü olabilirlik fonksiyonunu maksimize eden μ değeri bulunmakta iken σ anakütle parametresi olan σya bağımlı olmayan bir sabittir. Bundan dolayı ilk olarakμ değeri bulunur; bu değer olabilirlik fonksiyonundaki μ değişkeni yerine konulur ve bu yeni tek değişkenli fonksiyonu maksimize eden σ değeri bulunur.
olabilirlik fonksiyonunun şu toplam ifadesinin bir azalan fonksiyonu olduğu bilinmektedir:
Bu toplam ifadeyi minimize edecek μ değerini bulmak istenmektedir. Şu ifade
n gözleme dayanan bir "örneklem ortalamasıdır. Böylece
Bu ifadede so terim μ değişkenine bağlıdır ve bu terimin minimum değeri şöyle bulunur:
İşte bu ifade n sayıda X1,....,Xn gözlem kullanarak μnun maksimum olabilirlik kestirimidir. Sonuç olarak
elde edilir. olabilirlik fonksiyonunun logaritmasi olan log-olabilirlik fonksiyonu matematik notasyona göre küçük harflerle (yani, yazılması alışılagelmiştir.
Sonra
olur. Bu türev, σ2 değeri 0 ile
değeri arasında ise pozitif olur; bu değere eşitse türev sıfıra eşittir; bu değerden büyükse türev negatif olur.
Bu analizin sonucu olarak bu bulunan artıklar n gözlemli örneklem için σ2 bir maksimum olabilirlik kestirimidir ve bunun kare kökü σ için maksimum olabilirlik kestirimdir. Bu kestirim yani bir yanlı kestirimdir. Alışılagelen yansız kestirim n/(n - 1) çarpı bu kestirimdir. Ancak yanlı maksimum olabilirlik kestirimi için ortalama hata karesi yansız kestirimden daha küçüktür.
Parametrelerin yansız kestirimi[değiştir | kaynağı değiştir]
Bir örneklemden elde edilen anakütle ortalamasının maksimum olabilirlik kestirimcisi, anakütle ortalamasının yansız kestirimcisiolarak bilinir. Aynı şekilde anakütle ortalaması önsel olarak bilinirse, varyans için maksimum olabilirlik kestrimcisi de yansız kestirimcidir. Ancak eğer elimizde bir örneklem bulunuyorsa ama bu örneklemin geldiği anakütlenin ne ortalamasının ne de varyansının değerlerin bilmiyorsak, anakütle varyansının yansız kestrimicisi, , şöyle ifade edilir:
Eğer tüm Xi birbirinden bağımsız ve aynı şekilde dağılım gösterirlerse, bu "örneklem varyansı" bir Gamma dağılımıgösterir:
Ayrıca bakınız[değiştir | kaynağı değiştir]
- Standart normal dağılım
- Veri dönüşümleri (istatistik) - Verileri normal dağılıma dönüştürmek için basit teknikler
- Erdős-Kac teoremi, Sayı teorisi içinde normal dağılımın meydana çıkışı.
-
- Iannis Xenakis, Müzik için Gauss-tipi dağılımı.
- Ters Gauss-tipi dağılım
- Log-normal dağılım
- Çokdeğişirli normal dağılım
- Matris normal dağılımı
- Normal dağılım gösterme ve korelasyon olmaması bağımsızlık ifade etmez.(İki tane birbirinden bağımsız olmadan birbirleri ile korelasyon göstermeyen normal dağılımlı rassal değişken için örnek verilmiştir. Bu örnek çokludeğişirli normal dağılım için geçerli değildir.)
- Student'in t dağılımı
Kaynakça[değiştir | kaynağı değiştir]
- ^ H. Gavil, 2003
Dış bağlantılar[değiştir | kaynağı değiştir]
Normal dağılım[değiştir | kaynağı değiştir]
- Mathworld: Normal dağılım 5 Temmuz 2008 tarihinde Wayback Machine sitesinde arşivlendi.
- GNU Bilimsel Kutuphane – Referans Elkitabı–Gauss-tipi dağılım 8 Haziran 2008 tarihinde Wayback Machine sitesinde arşivlendi.
- PlanetMath: Normal rassal değişken 16 Mayıs 2008 tarihinde Wayback Machine sitesinde arşivlendi.
- Sezgi yoluyla normal dağılım türetme
- Normal dağılım Karl Gauss tarafında mı bulunmuştur? Euler'in bulduğu gamma fonksiyonlari ailesi ve bunların istatistik tarihindeki yeri
- Maxwell şeytanları: Propozisyonlu dgiskenler hesabi fonksiyonlari kullanarak olasilik dağılımlarının simulasyonu
Yazılım sonuçları ve uygulamaları[değiştir | kaynağı değiştir]
- Normal dağılım tablosu 18 Aralık 2020 tarihinde Wayback Machine sitesinde arşivlendi.
- Kümülatif Normal dağılım hesaplama
- Dağılım hesaplayıcısı – Normal, t, ki-kare ve F-dağılımı için kritik değerler ve olasılık hesaplayıcısı29 Ocak 2007 tarihinde Wayback Machine sitesinde arşivlendi.
- Normal dağılımlar için Java Appleti 20 Mart 2008 tarihinde Wayback Machine sitesinde arşivlendi.
- Etkilişimli (normal dağılım da dahil) dağılım modelcisi 16 Şubat 2008 tarihinde Wayback Machine sitesinde arşivlendi.
- Normal eğrisi altındaki alan hesaplayıcısı - Daniel Soper'in Free Statistics Calculators websitesi
- Etkileşimli Standart normal eğrisi gösterimi 22 Şubat 2008 tarihinde Wayback Machine sitesinde arşivlendi. Standart normal eğrinin tek kuyruk ve iki kuyruk alanı için çabuk göz önüne getirme yazılımı.
- Online hesap makinesi Normal dağılım 10 Mart 2014 tarihinde Wayback Machine sitesinde arşivlendi.
Algoritmalar ve yaklaşımlar[değiştir | kaynağı değiştir]
- Calculating the Cumulative Normal distribution, C++, VBA, sitmo.com
- Normal birikimli dağılım fonksiyonunun tersini hesaplamak icin bir algoritma. , Hazırlayan: Peter J. Acklam – Birkaç değişik yazılım diliyle örnekler var.
- Ters Normal(0,1) dağılımına bir yaklaşım, gatech.edu
- Matematiksel Fonksiyonlar için Elkitabı': P(x) ve Z(x) icin Polinom ve Rasyonel Yaklaşımlar 17 Nisan 2008 tarihinde Wayback Machine sitesinde arşivlendi. - Abramowitz ve Stegun
















![{\displaystyle \Phi (x)={\frac {1}{2}}{\Bigl [}1+\operatorname {erf} {\Bigl (}{\frac {x}{\sqrt {2}}}{\Bigr )}{\Bigr ]},\quad x\in \mathbb {R} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ecde4ff96203d7422e37ed86d92586a1adc99555)
![{\displaystyle \Phi _{\mu ,\sigma ^{2}}(x)={\frac {1}{2}}{\Bigl [}1+\operatorname {erf} {\Bigl (}{\frac {x-\mu }{\sigma {\sqrt {2}}}}{\Bigr )}{\Bigr ]},\quad x\in \mathbb {R} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c15af2951c22da89b83947da223d8f54425cbdbe)











![{\displaystyle {\begin{aligned}M_{X}(t)&{}=\mathrm {E} \left[\exp {(tX)}\right]\\&{}=\int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}\exp {\left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)}\exp {(tx)}\,dx\\&{}=\exp {\left(\mu t+{\frac {\sigma ^{2}t^{2}}{2}}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad83ee58fe6f2461b98945aca57bcbf1bce5f3e8)




![{\displaystyle {\begin{aligned}\chi _{X}(t;\mu ,\sigma )&{}=M_{X}(it)=\mathrm {E} \left[\exp(itX)\right]\\&{}=\int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)\exp(itx)\,dx\\&{}=\exp \left(i\mu t-{\frac {\sigma ^{2}t^{2}}{2}}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6fe9d35f4cd6fc7ce19b884585df05c60d1b6b7)





































![{\displaystyle E\left[x^{2k}\right]={\frac {(2k)!}{2^{k}k!}}\sigma ^{2k}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/562f7b566aeae87e048a4e6b3516e0d00b3f3bb8)
















































