Binom dağılımı
Olasılık kütle fonksiyonu Eğriyi daha açık göstermek için noktalar çizgilerle birleştirilmiştir. | |
Yığmalı dağılım fonksiyonu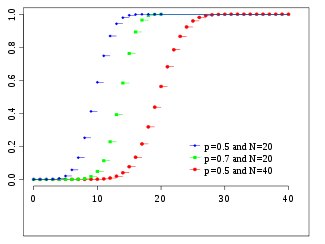 Renkler yukarıdaki çizgi renklerine uyar. | |
| Parametreler | deneyleme sayısı kesirsiz (tam sayı) başarı olasılığı (reel) |
|---|---|
| Destek | |
| Olasılık kütle fonksiyonu (OYF) | |
| Birikimli dağılım fonksiyonu (YDF) | |
| Ortalama | |
| Medyan | biri |
| Mod | |
| Varyans | |
| Çarpıklık | |
| Fazladan basıklık | |
| Entropi | |
| Moment üreten fonksiyon (mf) | |
| Karakteristik fonksiyon | |
Olasılık kuramı ve istatistik bilim kollarında, binom dağılımı n sayıda iki kategori (yani başarı/başarısızlık, evet / hayır, 1/0 vb) sonucu veren denemelere uygulanır. Araştırıcının ilgi gösterdiği kategori başarı olarak adlandırılır. Bu türlü her bir deneyde, bağımsız olarak, başarı (=evet=1) olasılığının p olduğu (ve yalnızca iki kategori sonuç mümkün olduğu için başarısızlık olasılığının 1 - p olduğu) bilinir. Bu türlü bağımsız n sayıda denemeler serisi içinde elde edilen başarı sayısının ayrık olasılık dağılımı binom dağılım olarak tanımlanır. Bir binom dağılım sadece iki parametre ile, yani n ve p, ile tam olarak tanımlanır. Matematik notasyon olarak bir rassal değişken X binom dağılım gösterirse şöyle ifade edilir:
- X ~ B(n,p)
Bu şekilde başarı/başarısızlık sonucu veren her bir deneme Bernoulli denemesi olarak da anılır. Eğer n=1 olursa, bu binom dağılım, yani B(1, p), gerçekte bir Bernoulli dağılımı ile aynıdır. Binom dağılımı çıkarımsal istatistik analiz ve pratik problem çözüm çabaları içinde çok popüler olan kullanılan binom testi için temel teoriyi ortaya çıkarır.
Örnekler[değiştir | kaynağı değiştir]
Binom dağılımı için en basit örnek bir zarın 10 defa atılıp kaç tane 6 elde edildiğinin sayılmasıdır. Bu rassal sayının (yani 10 deneyde kaç tane 6 elde edilmesi) dağılımı, n=10 ve p=1/6 parametreleri olan bir binom dağılımdır.
Diğer bir örnek, çok büyük bir halk kitlesinin içinde yeşil gözlü olanların incelenmesinden ortaya çıkar. Araştırmamız yeşil gözlüler hakkında olduğu için başarı kategorisi yeşil gözlü kişi gözlemi için kullanılır ve başarısızlık kategorisi yeşil gözlü olmayan kişi gözlemi karşılığı olarak ele alınır. Bu halk kitlesi içindeki yeşil gözlüler oranının, (yani başarı olasılığının) %5 olduğu bilinsin. 100 kişiyi kapsayan bir basit rastgele örneklem seçelim ve örneklem içinde bulunan her bir kişinin göz rengini gözleyelim. Bu işlemin binom dağılım açıklamasına göre karşılığı 100 tane bağımsız deneme yapılmasıdır yani n=100 dur. Bu örnekte içinde gözlemi yapılan yeşil gözlü kişi sayısı, 0 ile 100 arasında değerler alabilen, X rassal değişken olarak kabul edilsin. X için olasılık n=100 ve p=0.05 parametreleri olan bir binom dağılım ile bulunur.
Tanımlama[değiştir | kaynağı değiştir]

Olasılık kütle fonksiyonu[değiştir | kaynağı değiştir]
Genel olarak, eğer bir rassal değişken K n ve p parametresi olan bir binom dağılım gösterirse, şöyle ifade edilir:
- K ~ B(n, p).
Tam k sayıda başarı elde etmek için olasılık şu olasılık kütle fonksiyonu ile açıklanır:
burada k = 0, 1, 2, ..., n ve
terimi binom katsayısıdır yani "n'nin k'li kombinasyonu" olur. Bunun değişik bir ifadesi
- C(n, k) veya nCk
olarak verilebilir. Böylece dağılımın adının nereden ortaya çıkartıldığı görülmektedir. Bu formülün biraz daha detaylı açıklanması şöyle yapılabilir. k sayıda başarı (pk) ve n - k sayıda başarısızlık (1 - p)n - k istemekteyiz. Ancak, k sayıda başarı n sayıda denemenin belirli olmayan her bir tarafında ortaya çıkabilir. n deneme sayısı içinde k başarı sayısı C(n,k) değişik şekilde yerleştirilebilir.
Binom dağılıma uyan problemlerde olasılık bulmak için hazırlanmış referans tablosu bir sıra alt-tablodan oluşur ve her bir alt-tablo n/2 sayıya kadar değerle ile doldurulur. k>n/2 olduğu için olasılık değeri şu formülün uygulaması ile
bulunur. Böylece aranan olasılık değeri (binom genellikle simetrik olmadığı için) tablolarda gösterilen değişik değerde k ve değişik değerde p kullanarak bulunur.
Yığmalı dağılım fonksiyonu[değiştir | kaynağı değiştir]
Yığmalı dağılım fonksiyonu bir tanzim edilmiş tam olmayan beta fonksiyonu kullanılması ile şöyle ifade edilebilir:
Ancak k 'in kesirsiz bir tam sayı ve
- 0 ≤ k ≤ n
olması gereklidir.
Eğer x gerçek bir tam sayı değilse veya pozitif değerde değilse, bu ifade şu alternatif şekle getirilebilir
Eğer k ≤ np ise dağılım fonksiyonun aşağı kuyruk tarafı için yukarı sınırlar değerleri ortaya çıkartılabilir. Özellikle, önce Hoeffding'in eşitsizliği kullanılarak sınır değeri şöyle bulunur:
ve sonra Chernoff'un eşitsizliği kullanılarak şu sınır ortaya çıkartılır:
Ortalama, varyans ve mod[değiştir | kaynağı değiştir]
Eğer X binom dağılım gösteren bir rassal değişken ise, bu gerçek şöyle ifade edilir. X ~ B(n,p) ise, X in beklenen değeri
olur ve varyans değeri ise
olur.
Bu gerçeğin ispatı şöyle yapılabilir: Önce yalnız tek bir Bernoulli denemesi incelensin. Bunun sonucu ya 1 (başarı) veya 0 olabilir; bunların olasılıkları sırasıyla p ve 1 - p olur. Bu deneyin ortalamasının μ = p olduğu bilinmektedir. Varyans ise tanımına göre
olur. Şimdi n sayıda Bernoulli denemesi (yani genel bir binom dağılımı) ele alındığı kabul edilsin. Eğer denemelerin her biri bağımsız ise, her bir denemenin varyansı diğer deneme varyanslarıyla birlikte toplamları alınırsa şu ifadeyi elde edilir:
X in mod değerini bulmak için bir tam sayı olan
- m = (n + 1)p
ifadesi tanımlanır ve X in (n + 1)p değerinden daha eksik değerde veya ayni değerde en büyük tam sayı olduğu bilinir. Böylece hem m - 1 hem de m iki ayrı mod değeri oluştururlar.
Burada dikkat edilmesi gereken bir gerçek de binom dağılımının çift mod göstermesine rağmen her çift mod gösteren dağılımın bir binom dağılımı olmadığıdır.
Ortalama ve varyansın açık olarak elde edilmeleri[değiştir | kaynağı değiştir]
Binom dağılım için ortalama ve varyans değerleri açıkça ilk tanımsal prensipler kullanılarak elde edilebilirler. Bu iki değerin ortaya çıkartılması için şu toplamlar kullanılır. Bu toplamlardaki terimlerin yerleri değiştirilerek binom [[Binom Dağılım#Olasılık kütle fonksiyonu]|olasılık kütle fonksiyonu]]nun tümünde toplamın her zaman 1'e eşit olmasını sağlarız.
Ortalama[değiştir | kaynağı değiştir]
Bir ayrık rassal değişken için beklenen değer tanımını bir binom dağılım için uygulanir.
Bu seride k=0 indeksli birinci terimin değeri 0 'a eşittir; çünkü birinci faktör k sıfırdır. Bunu bertaraf edersek alt limiti k=1 'e indirgenmiş olunur.
Faktör ifadelerinden n ile k faktörlerini çekip alırsak ve p için birinci üssü ayırılırsa; indekslerin yeniden tanımlanmasına hazırlanmış olur:
Yeni isim olarak m = n - 1 ve s = k - 1 kullanabilir. Bu işlem yapılması ile toplamın değeri değişmez, ama daha kolayca tanımlanan şu ifade ortaya çıkar:
Ortaya çıkan toplam bir binom dağılımının tümü için toplamdır (Olasılık kütle fonksiyonu ortaya çıktığı gibi ilk toplamdan bir sıra alttadır). Böylece
Varyans[değiştir | kaynağı değiştir]
Varyans değeri şöyle tanımlanmaktadır:
(bak: varyans, 10. Varyans için hesaplama formülü):
Bu formülün kullanılışında görülmektedir ki X2 ifadesinin beklenen değerinin de hesaplanması gerekmektedir. Bu değer şu formüle göre bulunabilir:
Yukarıda ortalama formülünü elde etmeye çalışırken kullandığımız yöntemi kullanarak, k nin bir faktörünün değeri açığa çıkartılabilir ve böylece şu ifade elde edilir:
(tekrar, m = n - 1 ve s = k - 1). Bu toplamı iki değişik toplama ayırabiliriz ve her bir toplam ifadesi şöyle bulunur:
Birinci toplam yukarıda ortalama bulurken ortaya çıkardığımız ifadenin aynıdır ve mp değerine eşittir. İkinci toplam değer ise 1'e eşit olur.
Bu sonucu varyans için ifadenin içine koyarsak ve ortalama için ifadeyi de, yani (E(X) = np) de, konulursa varyans için şu formülü elde edilir:
iLa
Diğer dağılımlarla ilişkiler[değiştir | kaynağı değiştir]
Binom değerlerin toplamı[değiştir | kaynağı değiştir]
Eğer X ~ B(n, p) ve Y ~ B(m, p) iki bağımsız binom dağılımlı değişken iseler, o zaman X + Y toplam ifadesi de bir binom dağılımlı değişkendir. Bu toplam değişkenin dağılımı
olarak ifade edilir.
Normal yaklaşım[değiştir | kaynağı değiştir]

Eğer n yeterce büyük ise, dağılımın çarpıklığı çok bariz olmaz ve uygun bir süreklilik doğrulaması kullanılırsa, B(n,p) olarak tanımlanan bir binom dağılım yerine
ile tanımlanan bir simetrik normal dağılım çok iyi bir yaklaşık olarak kullanılabilir.
n değerinin yeter derecede büyük olup olmadığını tespit etmek için çeşitli amprik kurallar kullanılabilir. Bir amprik kurala göre hem np ve hem de n(1 - p) 5'ten daha büyük olmalıdır. Fakat değişik istatistik otoriteleri değişik değerler de kabul etmektedirler; örneğin bazı kaynaklara göre gereken değerler 10'u aşmalıdır. Hangi değerlerin kullanılacağı arzu edilen yaklaşım dakikliğine bağlıdır. Çokça kullanılan diğer bir ampirik kural ise şu eşitlik ifadesinin
bulunup bulunmadığına dayanır.
Süreklilik doğrulaması operasyonunun kullanışı şu örnek ile gösterilebilir. Bir binom rassal değişken X için olasılığı, yani Pr(X ≤ 8) değerini, bulmak istediği kabul edilsin. Eğer Y rassal değişkeninin normal yaklaşım ile verilen bir dağılımı varsa Pr(X ≤ 8) değeri Pr(Y ≤ 8.5) ifadesi ile yaklaşık olarak bulunabilir. Burada ikinci terime 0.5 eklenmesi (yani 8 yerine 8.5 kullanılması) süreklilik doğrulaması operasyonudur; eğer bu kullanılmasaydı, doğrulama yapılmamış normal yaklaşık değer daha az dakik sonuçlar vereceği bilinmektedir.
Büyük değerde n için doğru binom formülü kullanarak hesap yapılması çok büyük emek gerektirmekte olduğu için, özellikle bilgisayarların hemen el altında olmadığı günlerde, bu yaklaşım çok büyük zaman ve emek tasarrufu sağlamaktaydı. Normal dağılım ile yaklaşım ilk olarak 1733de Abraham de Moivre tarafından Şanslar için Doktrin adlı kitabında ortaya atılmıştır. Sonradan bu yaklaşımın kullanışı, B(n,p) n sayıda bağımsız ve tıpatıp ayni şekilde dağılım gösteren 0-1 değerli gösterge değişkeni olduğu için, merkezsel limit teoreminin bir sonucu olarak görülmektedir.
Örneğin, büyük bir anakütleden gelen n kişilik bir örnek alarak, bir cümle vererek bir belirli fikirin kabul edilip edilmediğini öğrenmek istediğimizi düşünelim. Bu fikri kabul edenler oranı, tabiidir ki kullanılan örneğe bağlı olacaktır. Eğer n sayıda kişi kapsayan birçok gerçekten rassal olan örnekleri tekrar tekrar bulunarak, bu fikri kabul edenlerin oranı ortalaması gerçek anakütle kabul edenler oranı olan p olan ve standart sapması
σ = (p(1 - p)n)1/2
olan bir normal dağılım ile yaklaşım sağlanabilecektir. Örnek büyüklüğü olan n in büyük olma halinde yaklaşım sonucu iyi olacaktır, çünkü beklenen değerlerin bir oranı küçüldükçe bilinmeyen p parametresini yaklaşım değeri daha dakik olmasını sağlamaktadır.
Poisson yaklaşımı[değiştir | kaynağı değiştir]
np çarpım ifadesi değişmeden kalırken, deneyleme sayısı sonsuzluk değerine yaklaşırsa, binom dağılımı Poisson dağılımına yaklaşım gösterir. Buna dayanarak, eğer n yeter derecede büyük ve ve p yeter derecede küçük ise, B(n,p) ile tanımlanan bir binom dağılımı yerine λ = np parametreli bir Poisson dağılımı yaklaşık olarak kullanılabilir. Bu yaklaşımını uygun olarak kullanılabilmesi için empirik olarak parametrelerin şu değerlere uyması gerektiği kabul edilmiştir:
- ya n ≥ 20 ve p ≤ 0.05
- yahut da n ≥ 100 ve np ≤ 10.[1]
Binom dağılımlar için limitleri[değiştir | kaynağı değiştir]
- n değeri ∞'ye yaklaşırken ve p 0'a yaklaşırken, eğer np değeri değişmeden λ > 0 olarak kalırsa veya asgari olarak np λ > 0 değerine yaklaşırsa, o zaman (n, p) parametreli Binom dağılımı, λ beklenen değeri olan bir Poisson dağılımına yaklaşır.
- Eğer p değeri değişmeden kalırken, n' değeri ∞'ye yaklaşırsa
teriminin dağılım beklenen değeri 0 ve varyans değeri 1 olan bir normal dağılıma yaklaşır. (Bu Merkezsel limit teoreminin özel bir halidir.)
Ayrıca bakınız[değiştir | kaynağı değiştir]
- Galton kutusu
- Beta dağılımı
- Hipergeometrik dağılım
- Multinom dağılımı
- Negatif binom dağılımı
- Poisson dağılımı
- SOCR
- Normal dağılım
Kaynakça[değiştir | kaynağı değiştir]
- ^ NIST/SEMATECH, '6.3.3.1. Counts Control Charts', e-Handbook of Statistical Methods, <http://www.itl.nist.gov/div898/handbook/pmc/section3/pmc331.htm 11 Mart 2008 tarihinde Wayback Machine sitesinde arşivlendi.> [accessed 25 October 2006]
- Luc Devroye, Non-Uniform Random Variate Generation, New York: Springer-Verlag, 1986. Özellikle Bölüm X, Aralıklı Tekdeğişirli Dağılımlar kısmına bakın.
- Voratas Kachitvichyanukul ve Bruce W. Schmeiser, Binomial random variate generation, Communications of the ACM 31(2):216–222, February 1988. DOI:10.1145/42372.42381
Dış bağlantılar[değiştir | kaynağı değiştir]
- Binom Olasılık Dağılım Hesaplayıcısı 2 Mart 2008 tarihinde Wayback Machine sitesinde arşivlendi.
- Binom Dağılımlı Olasılık İçin Basit Açıklama
- "Binomial Distribution" 26 Şubat 2008 tarihinde Wayback Machine sitesinde arşivlendi. hazırlayan : Chris Boucher, Wolfram Gösterim Projesi, 2007.








































![{\displaystyle \mu \pm 3\sigma =np\pm 3{\sqrt {np(1-p)}}\in [0,n].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a3c02d3280abc50642d9f441dd57ff349bdb3d8)
