Kondansatör

Kondansatör (bugünkü İngilizcede capacitor, "kapasitör") ya da sığaç[1] veya yoğunlaç[1], elektronların kutuplanıp elektriksel yükü elektrik alanın içerisinde depolayabilme özelliklerinden faydalanılarak bir yalıtkan malzemenin iki metal tabaka arasına yerleştirilmesiyle oluşturulan temel elektrik ve elektronik devre elemanı. Piyasada kapasite, kapasitör, sığaç gibi isimlerle anılan kondansatörler, 18. yüzyılda icat edilip geliştirilmeye başlanmış ve günümüzde teknolojinin ilerlemesinde büyük önemi olan elektrik-elektronik dallarının en vazgeçilmez unsurlarından biri olmuştur. Elektrik yükü depolama, reaktif güç kontrolü, bilgi kaybı engelleme, AC/DC arasında dönüşüm yapmada kullanılır ve tüm entegre elektronik devrelerin vazgeçilmez elemanıdır. Kondansatörlerin karakteristikleri olarak;
- Plakalar arasında kullanılan yalıtkanın cinsi,
- Çalışma ve dayanma gerilimleri,
- Depolayabildikleri yük miktarı
sayılabilir. Bu kriterler göz önünde bulundurulduktan sonra gereksinime uygun olan kondansatör tercih edilir. Kondansatörlerin fiziksel büyüklükleri, çalışma gerilimleri ve depolayabilecekleri yük miktarına bağlıdır. Tasarım açısından ise çeşitlilik boldur, hemen hemen her boyut ve şekilde kondansatör temin edilebilir.


Tarihçe[değiştir | kaynağı değiştir]
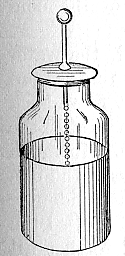
Elektrik konusunun gelişmesi 18. yüzyılda statik (durgun) elektriğin incelenmesiyle başlamıştır.[2] Statik elektriğin bir ip boyunca iletilebilmesi, elektrik yükünün temasla paylaşılabilmesi ve depolanabilmesi özellikleri araştırmacı bilim adamları tarafından keşfedilmeye başlanmıştı. 1745 yılında Ewald Georg von Kleist elektriği küçük metal bir şişede depolamayı başarmıştı. Ancak kondansatörün asıl gelişmesi, Leiden'de elektrik üzerinde deneyler yapan Pieter van Musschenbroek'in çalışmaları sonucu gerçekleşmişti.[3]

Musschenbroek bir rastlantı sonucu Kleist'in çalışmalarını doğrular nitelikte sonuçlara erişti. Musschenbroek içi ve dışı metalle kaplı cam bir şişe tasarladı. Şişenin bir kısmı suyla doldurulmuş ve ağzı hava - sıvı geçirmeyecek şekilde mantarla tıkanmıştı. Mantarın ortasından geçen iletken, bir ucu şişenin dışında bir ucu suyun içinde olacak şekilde yerleştirilmişti. İletkene statik elektrik üretici temas ettiğinde Leiden şişesi yük depolamakta, elektriği ileten başka bir malzeme temas ettiğinde boşalmaktaydı.[4] Bu şişeler aynı zamanda ilk kondansatörlerdi.[2] Bu nedenle, şu anda Farad olan kapasite birimi ilk zamanlarda jar (şişe) olarak kabul edilmişti. Bu birim bugün 1 nF kapasiteye tekabül eder.
Denemeler sonucunda metal kaplamalar arasındaki cam inceldikçe yayılan kıvılcımın büyüdüğü gözlendi. Leyden şişesinde depolanan yük büyük değerler alabiliyordu ve birbirine tellerle bağlanmış şişelerden boşalan elektriğin hayvanları öldürebileceği gözlenmişti.[2] Bu ilginç alet Ewald Jürgen Georg von Kleist'ın keşfi, Pieter van Musschenbroek'in geliştirmesiyle ortaya çıkmıştır. Amerikalı devlet adamı ve bilimci Benjamin Franklin, cam yalıtkanın Leyden şişesinden farklı olarak oval değil düzlemsel olmasının aynı işlevi gördüğünü bulmuş, Franklin'in düzlemsel cam yalıtkanlı kondansatörüne Franklin Düzlemleri adı verilmiştir.[4] Ardından Alessandro Volta ve Nikola Tesla gibi birçok bilim adamı tarafından incelenen kondansatör geliştirilerek günümüzdeki şeklini almıştır. Kondansatörler ismini, İtalyanca condensatore kelimesinden alır. Kapasite birimi ise jar'dan sonra, İngiliz bilim adamı Michael Faraday'ın isminden hareketle Farad seçilmiştir.
Kapasite değerinin okunması[değiştir | kaynağı değiştir]


→ Mavi: 400 Volt – 2.2 mikroFarad = 2.2 µF
→ Sarı: 222J = 2200 pikoFarad ± % 5 = 2.09 nF < C < 2.31 nF
Kondansatörlerde temel olarak iki değişken, tüketici için seçme olanağı sunar ve kondansatörler arasındaki farkları oluşturur. Bunlar, kondansatörün çalışma – dayanma gerilim değeri ve depolayabileceği yük miktarıdır ve bunlar her kondansatörün üzerinde belirtilmiş olmak zorundadır. Bazı kondansatörlerin üzerinde çalışma değeri doğrudan yazılı iken bazılarında rakamlar ve renkler kullanılır.[5] Direkt değerleri yazılı olanlar kolay okunmasına karşın, rakam ve renk kodlu olanların okunması belli standartlara bağlıdır.
Rakam kodları[değiştir | kaynağı değiştir]
Rakam kodlarının standartları bir liste şeklinde verilebilir.[5]
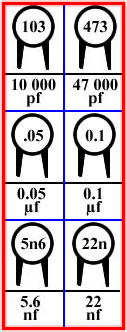
- Kondansatörün üzerinde kapasite değeri 3 rakam ve toleransı ise bir harf ile belirtilir.
10000 pF = 10 nF olarak bulunur.
- Eğer rakam kodları arasında nokta (.) kullanılıyorsa, yazılan sayı kapasiteyi doğrudan
mikroFarad (µF) olarak verir. Resimde ortadaki kondansatörde görülen 0.1 yazısı kapasitenin 0,1 µF olduğunu gösterir.
- Rakam kodlarının arasında p, n, µ, m harflerinden biri kullanılıyorsa, harfin olduğu yerde ondalık kısım devreye girer ve değer de harfin cinsinden okunur. Örneğin resimde alttaki kondansatörde yazan 5n6 ifadesi, kapasitenin 5,6 nF olduğunu belirtir.
- Üçüncü rakam bazı istisnai durumlarda farklı anlamlar taşır. Üçüncü rakam, 1 - 5 arasında koyulması gereken sıfır sayısını belirtirken, hiçbir zaman 6 & 7 değerlerini alamaz. 8 & 9 sayıları ise sırayla
0,01 & 0,1 çarpanlarını belirtir.
- Kapasite, bazı durumlarda tam yazılan değerde olmaz, bu sebeple belli oranlarda oynamalar olacağı göz önünde bulundurulur ve rakam kodlarının sonuna büyük harfler koyulur. Bu harfler de bize toleransın oranını belirtir.[6] Aşağıdaki tabloda bu harflerin hangi tolerans değerini belirttiği sıralanmıştır.
Simetrik tolerans ifade eden kodlar
| B = ± % 0,10 | C = ± % 0,25 | D = ± % 0,5 |
|---|---|---|
| F = ± % 1 | G = ± % 2 | J = ± % 5 |
| K = ± % 10 | L = ± % 0,01 | M = ± % 20 |
| N = ± % 30 | P = ± % 0,02 | W = ± % 0,05 |
Simetrik olmayan tolerans ifade eden kodlar
| Q = - % 10, + % 30 | S = - % 20, + % 50 |
|---|---|
| T = - % 10, + % 50 | Z = - % 20, + % 80 |
Renk kodları[değiştir | kaynağı değiştir]
Rakam kodlarından başka, bazı kondansatör çeşitlerinde de renk kodları kullanılır. Özellikle seramik, tantalum ve polyester kondansatörlerde renk kodları yaygındır. Aşağıdaki liste renk kodlarının anlamlarını sıralarken,[5] yandaki resimlerde de çeşitli örnekler görülebilir.

| Seramik | Tantalum | Polyester | ||||||
| Renk | Değer | Çarpan | T | V | T | V | T | V |
| Siyah | 0 | 100 | 2 pF | - | % 10 | 10 V | % 20 | - |
| Kahve | 1 | 101 | % 1 | - | % 1 | - | - | 100 V |
| Kırmızı | 2 | 102 | % 2 | - | % 2 | - | - | 250 V |
| Turuncu | 3 | 103 | - | - | - | - | - | - |
| Sarı | 4 | 104 | - | - | - | 6,3 V | - | 400 V |
| Yeşil | 5 | 105 | % 5 | - | % 5 | 16 V | % 5 | - |
| Mavi | 6 | 106 | - | - | - | 20 V | - | - |
| Mor | 7 | 107 | - | - | - | - | - | - |
| Gri | 8 | 0.01 | - | - | - | 25 V | - | - |
| Beyaz | 9 | 0.1 | % 10 | - | % 10 | 3 V | % 10 | - |
- Seramik kondansatörlerde kodlar, renk çubuklarından hangisi kenara en yakınsa ondan başlanarak okunur. Tantalum ve polyester kondansatörlerde mevcut renk sırası ise resimde görüldüğü gibidir.
- 1 ve 2 numaralı renkler anlamlı sayı dizisidir ve aynen yazılır. Ç (çarpan) harfinin belirttiği renkler anlamlı rakamların yanına eklenecek sıfır sayısını belirtir. T (tolerans) kapasite değerindeki oynamayı, V (gerilim) ise kondansatörün çalışma gerilimini gösterir.
Harf kodları[değiştir | kaynağı değiştir]
Harf kodları kondansatörler üzerindeki toleransı veya sıcaklık katsayısını belirtmek için kullanılır. Tolerans değeri için rakam kodunun yanına bir büyük harf yerleştirilir. Bu harfin anlamı rakam kodları bölümünde yazmaktadır. Sıcaklık katsayısını belirtmek için ise harflerden oluşan bir dizi kullanılır.
Yalıtkan malzemelerin çoğunda sıcaklıkla kapasite değişmemesine rağmen bazı malzemelerde değişim olur. Sıcaklık katsayısı, bir malzemenin sıcaklıkla kapasite değişimini belirten katsayıdır. İngilizcesi temperature coefficient (tempco) olan bu katsayının birimi 'dir.[8] Uygulamada ise ifadesiyle karşılaşılır. ppm sözcüğü milyonda bir katsayısının İngilizce baş harflerinden oluşturulmuştur.

Bazı yalıtkan malzemelerin sıcaklıkla kapasite değişimi eğrisi düz kabul edilebilecek şekildedir.[9] Ancak seramik yalıtkanın kapasitesi sıcaklık değişimine çok duyarlıdır ve büyük değişimler gösterir,[10][11] öyle ki seramik kondansatörlerin üstünde belirtilen değerler sadece oda sıcaklığında (25 °C ~ 77 °F) geçerlidir. Sıcaklık katsayısı kondansatörlerin üzerinde bir harf dizisi kodla belirtilir ve aşağıdaki liste bu harflerin anlamını belirtir. Yandaki resimde bazı sıcaklık katsayısı kodlarının anlamları ve okunuş şekilleri verilmiştir.
- P (positive change - pozitif değişim): Kapasite değerindeki değişimin sıcaklıkla arttığını anlatan harftir. Örneğin P100 ifadesi, sıcaklıkta milyonda bir derecelik bir artışın, kapasiteyi 100 parça artırdığını belirtir.[12]
- N (negative change - negatif değişim): Kapasite değerinin sıcaklık arttıkça azaldığını yani sıcaklıkla kapasitenin ters orantılı olarak değiştiğini belirtir. Örneğin üzerinde N1500 yazan bir seramik kondansatörün milyonda bir derecelik sıcaklık artışında, kapasitesi 1500 parça azalır.[12]
- NP0 (neg/pos/zero) - C0G (change zero): Sıcaklık nasıl değişirse değişsin kapasite değerinin hemen hemen sabit kaldığını belirtir.[12]
- GMV (guaranteed minimum value): Seramik kondansatörün üzerinde belirtilen kapasite değerinin, oda sıcaklığında garantilenmiş en küçük kapasite değeri olduğunu belirtir. Yani, kondansatörün kapasitesi çok daha büyük olabilir. Kapasite değerinin öneminin olmadığı uygulamalarda bu kondansatörler kullanılabilir.[12]
Çeşitleri[değiştir | kaynağı değiştir]
Yalıtkan cinsine göre[değiştir | kaynağı değiştir]

Kondansatörleri sınıflandırmada en çok kullanılan yöntem yalıtkan maddesine göre sınıflandırmadır. Malzemelerin bağıl yalıtkanlık katsayısı ve delinme gerilimleri yalıtkanlar arasındaki farklılıkları oluşturur ve bunlar kondansatörlerin özelliklerini belirleyip uygulama alanlarındaki çeşitliliği genişletir. Yandaki resimde farklı kondansatörlerin sahip olduğu farklı kapasite ve çalışma gerilim değeri aralıkları görülmektedir. Aşağıdaki listede ise yalıtkanları farklı olan kondansatörlerin birbirine göre farkları sıralanır.
- Vakumlu kondansatör: İki metal plakanın arasında havasız ortam bırakılır ve genelde cam veya seramik kaplanarak oluşturulur. Özellik olarak düşük yük kapasitesi (10 ~ 1000 pikoFarad) ve yüksek gerilime (10000 V'a kadar) dayanması gösterilebilir. Genelde radyo vericilerinde ve yüksek gerilim gerektiren uygulamalarda kullanılır.

- Havalı kondansatör: Metal plakaları arasında hava boşluğu bırakılmasıyla oluşturulan bu kondansatörlerde, plakalar genelde alüminyum ve gümüş kaplamalı olarak tasarlanır. Hava yalıtkanının dielektrik kaybı düşüktür. Hemen hemen tüm hava aralıklı kondansatörler ayarlanabilir olarak imal edilir ve radyo frekansı ayarlamada kullanılır. Ayrıca yüksek kapasite değerleri sunarlar.
- Plastik film kondansatör: Yüksek kaliteli polimer (polikarbonat, polyester, polipropilen ve yüksek kalite için polisülfon) tabakalarından üretilen plastik film kondansatörler sinyal ve filtre devrelerinde kullanım alanı bulur. Genelde kutupsuz olurlar.
- Mikalı kondansatör: Tasarım olarak metal filmli kondansatöre benzeyen mikalı kondansatör, çoğunlukla yüksek gerilim için kullanılır. Kapasite değerleri 50 pF ile 20 nF arasındadır. Tolerans değeri yüksektir ve yüksek frekansta çalışabilme özelliği vardır.
- Kâğıtlı kondansatör: İki uzun metal tabakanın arasına yağ emdirilmiş kâğıtların yerleştirilmesiyle elde edilir. 300 pF ile 4 µF arasında kapasite değeri alır ve delinme gerilimi, çalışma geriliminin 100 - 600 katı arasındadır. Eskiden radyo aksamında kullanılan bu kondansatör çeşidi görece yüksek gerilimlerde de kullanılır ancak kullanımı neredeyse tamamen bitmiştir.
- Camlı kondansatör: Yüksek gerilimde kullanılır ve pahalıdır. Pahalı olmasının sebebi yüksek kararlılıkta çalışması ve kapasite değerinin yüksek güvenilirliğe sahip olmasıdır. Geniş bir sıcaklık aralığında kararlı bir sıcaklık katsayısı vardır.
- Seramik kondansatör: Sırayla dizilmiş metal ve seramik tabakalarından oluşur. Yüksek hassasiyet gerektirmeyen kuplaj ve filtreleme işlemlerinde geniş bir kullanım alanı bulur. Yüksek frekans için uygundur.
- Alüminyum elektrolitik kondansatör: Kutuplu olarak imal edilir. Yapısı metal filmli kondansatöre benzemekle birlikte, daha fazla alan kaplaması açısından alüminyum plakalar asitle yakılır. Yalıtkan malzeme ise elektrolitle ıslatılır. Düşük sıcaklıklarda kapasite kaybına eğilim gösterir. Frekans karakterinin kötü olması yüksek frekanslarda kullanımını kısıtlamaktadır.
- Tantalum elektrolitik kondansatör: Alüminyum elektrolitik kondansatörle benzer özellikler gösterir ancak daha düzgün frekans ve sıcaklık karakteristiğine sahiptir. Kaçak akımı büyüktür ve düşük sıcaklıklarda performansı daha yüksektir.
- OSCON (OS-CON) kondansatör: Yalıtkan olarak polimerleştirilmiş organik yarı iletken katı elektrolitik bulundurur. Yüksek fiyatını uzun ömürlü oluşuyla telafi eder.
- Süper kondansatör: Karbon aerojelinden imal edilir. Oldukça fazla kapasite değeri sunar. Bazı uygulamalarda şarj edilebilir piller yerine kullanılır.
- Gimmick kondansatör: Yalıtılmış iki telin birbirine dolanmasıyla oluşturulur. Her bir tel bir plakayı temsil eder. Gimmick kondansatörü ayarlanabilir bir kondansatör şeklidir. Tellerin birbirine dolanması veya dolanmaması durumunda %20 kadar bir kapasite değişimi oluşur.
Yalıtkanları farklı olan kondansatörlerin karşılaştırılması
| Tantalum | Alüminyum | Seramik | Film | |
|---|---|---|---|---|
| Yalıtkan | Tantalum pentaoksit (Ta2O5) | Alüminyum oksit (Al2O3) | Baryum titanat türevleri | Polyester, polipropilin vb. |
| Dielektrik katsayısı | 27 | 8 ~ 10 | 1500 ~ 15000 (Baryum titanat) |
2.1 ~ 3.1 |
| Şekil ve tipi | Çip, batırma | Vida, soket, çip | Çip, batırma | Çip, batırma |
| Avantajları | Küçük boyutta görece yüksek kapasite, yarı kalıcı çalışma ömrü | Ucuz, küçük boyutta yüksek kapasite | Küçük boyut, kutupsuzluk | İyi karakteristik, yaygın çalışma gerilimi yelpazesi, yüksek güvenilirlik |
| Dezavantajları | Kısıtlı çalışma gerilimi yelpazesi, kutupluluk | Sıcak ortamda kısa çalışma ömrü, yüksek kapasite toleransı, kutupluluk | Kapasite değerinde sıcaklığa ve gerilime yüksek bağımlılık | Boyutta büyüklük |
Kapasite değerine göre[değiştir | kaynağı değiştir]
Kimi kondansatörlerin kapasiteleri değiştirilemez ve sabit kapasiteli olarak üretilirken, kimi kondansatörlerin kapasite değerleri üzerinde oynama, değişikliğe gitme imkânı vardır.
Sabit kondansatörler[değiştir | kaynağı değiştir]

Sabit kondansatörlerin üretim aşamasında belli olan kapasiteleri sonradan kullanıcı eliyle değiştirilemediğinden devreye ince ayar yapma imkânı yoktur. Kullanıcı önceden ihtiyacı olan çalışma değerlerini belirler, ardından ona göre uygun bir kondansatör temin eder. Sabit kondansatör olarak üstteki beş örnek sayılabilir. Bu kondansatör çeşitlerinin daha ayrıntılı anlatımları yalıtkanlarına göre kondansatörler bölümünde bulunabilir. Devrede gösteriliş şekilleri ise yandadır.
Ayarlanabilir kondansatörler[değiştir | kaynağı değiştir]


Kapasiteleri çeşitli yöntemlerle değiştirilebilen kondansatörlere ayarlanabilir kondansatör adı verilir. Bu halleriyle ince ayar yapmaya imkân tanırlar. Yandaki resim, devre üzerinde ayarlanabilir kondansatörlerin alabileceği simgelerdir. Üç çeşit ayarlanabilir kondansatörden bahsedilebilir.
Varyabl kondansatör
Birçok plakanın birbiri içine geçecek şekilde bağlanmasıyla elde edilen varyabl kondansatörler, iki parçadan oluşur: Sabit parça stator ve hareketli parça rotor. Rotora bağlı olan mil sayesinde plakalar birbiri içine doğru hareket eder veya uzaklaşır. Bu şekilde plakalar arası yüzey alanı kontrol edilir ve kapasite değerinde değişim olur. Varyabl kondansatörler, çok büyük kapasite değerlerine ulaşamasalar da
yüksek gerilim ve yüksek frekans değerlerinde çalışabilme olanağı sunarlar.
Trimer kondansatör
Trimerler, varyabl kondansatörlerden farklı olarak plakaların birbirine yaklaştırılması yöntemiyle kapasite değişimi sağlar. Küçük güç ve küçük boyutlu olup tornavida ile kontrol edilen trimerlerin kullanım alanı genel olarak telekomünikasyon devreleridir.
Varaktör
Diyot kullanılarak oluşturulmuş bir kondansatör çeşididir. Gerilim kontrollüdürler, uygulanan gerilim değeri büyüdükçe kapasite değerleri düşer. Yüksek frekansta çalışabilip telekomünikasyon alanında frekans kontrolünde kullanılırlar.
Kutup durumuna göre[değiştir | kaynağı değiştir]
Kondansatörler üretim aşamasında kutupları belirlenmiş olarak da tasarlanabilir. Bu duruma göre kondansatörler iki gruba ayrılır.

Kutupsuz kondansatör[değiştir | kaynağı değiştir]
Üretim aşamasında kutuplanmamış ve devreye bağlanma yönü önem taşımayan kondansatörlerdir. Seramik ve mika yalıtkanlı kondansatörlerlerin dahil olduğu bu grup, birkaç pikoFarad'dan mikroFarad değerlerine kadar bir yelpazede değer alır.

Kutuplu kondansatör[değiştir | kaynağı değiştir]
Üretilirken kutuplu olarak tasarlanan bu kondansatörün bir ve bir ucu vardır. Bu uçların devreye düzgün şekilde bağlanması gerekir. Aksi halde ciddi hasarlar oluşur çünkü ters bağlama halinde bu kondansatörler patlar. Kutuplu kondansatörler grubuna yalıtkanlarına göre kondansatörler bölümünde de anlatılan alüminyum elektrolitik ve tantalum kondansatörler girer. Bu kondansatörlerin kapasiteleri birkaç pikoFarad'dan başlar Farad ve üzerine kadar uzanan geniş bir yelpazede değer alır.
Sıvı tankı modellemesi[değiştir | kaynağı değiştir]
Elektrik, elektron hareketlerinin incelendiği, en küçük yapıtaşı elektron olan bir bilimken,hidrolik sıvıların mekanik özelliklerini inceleyen bir mühendislik ve bilim dalıdır. Elektrik ile hidrolik arasındaki benzetim yöntemi hesaplama ve elektriğin gözde canlanması açısından oldukça faydalıdır. Kondansatör analizi için gereken elektriksel birimlerin hidrolikteki karşılıkları aşağıdaki tabloda verilmiştir.
| Elektrik | Hidrolik |
|---|---|
| Elektron | Sıvı damlası |
| Gerilim | Sıvı basıncı |
| Akım | Sıvı akış hızı |
| Elektrik yükü | Sıvı miktarı |
| Kapasite | Sıvı tankının taban alanı |
| Frekans | Frekans |


Kondansatör, elektrik yükünü depolayan bir eleman olma özelliğiyle hidrolik bilimindeki sıvı tanklarına eşdeğerdir. Her yalıtkan malzemenin farklı yük depolama kapasitesi ve farklı bozulma gerilimi olduğu gibi, her sıvı tankının da bir basınç dayanımı ve sıvı miktarı kapasitesi vardır. Kondansatörlerde yalıtkan malzeme ne kadar önemliyse, sıvı tanklarında da sıvı ve tank çeşidi o kadar önemlidir.
Kondansatör kapasitesi, uygulanan gerilim başına depolanan yük miktarı olarak tanımlanır. Sıvı tankı kapasitesi ise tanka uygulanan basınç başına depolanan sıvı miktarıdır. Kondansatör uçları arasındaki gerilim farkı, sıvı tankına bağlı iki borudan geçen sıvıların basınç farkı olarak temsil edilir. Yandaki resimde kondansatörün ucu 25 Volt, ucu ise 10 Volttur ve 15 Volt fark, kondansatöre uygulanan gerilim farkıdır. Yine aynı resimde sıvı tankına sıvı basan pompanın basıncı 5 N/m², sıvıyı çeken pompanın basıncı ise 3 N/m²'dir, aradaki basınç farkı ise tankın uçları arasındaki basınç farkıdır. Kondansatör uçları arasındaki gerilim farkının plakalar arasında yük biriktirmesi gibi, tankın uçları arasındaki basınç farkı da tankta sıvı biriktirir. Tankın deforme olmaması için dış maddesinin, uçlar arasındaki basınç farkına dayanabilecek sağlamlıkta olması gerekir. Kondansatörlerin çalışma gerilimlerinin üzerindeki gerilimlerde deforme olmaları gibi, sıvı tankları da fazla basınçta patlarlar.
Tek yönlü sıvı akışı[değiştir | kaynağı değiştir]
Hidrolikte DC kaynak, içinden geçen sıvının basıncının, hızının ve yönünün hiç değişmediği sıvı pompasına benzetilebilir. Basınç farkı, bir tanka giren sıvı basıncıyla çıkan sıvı basıncı arasındaki farktır. Uçları arasında P sıvı basıncı olan bir tankın çıkış borusu kapalı farzedilip giriş borusundaki sıvı basıncı P olarak verilmesi benzetimi ve gerçekleşecek olaylar yandaki animasyonda gösterildiği gibidir.
Uçları arasında sıvı basınç farkı olan tankın içinde sıvı birikmesi başlar. İlk anda tank boş olduğundan, pompadan gelen sıvı basıncının önünde bir engel yoktur ve sıvı akış hızı en büyük halindedir. Tank dolmaya başladıkça biriken sıvı, ağırlığı dolayısıyla pompaya ters yönde ve zamanla artan bir basınç uygular, net basınç pompa sıvı basıncı ile tankta biriken sıvı basıncı arasındaki fark olduğundan basınç farkı zamanla azalır. Basınç farkının azalması, tanka sıvı giriş hızının azalması anlamı da taşıdığından tankın sıvıyla dolma hızı gittikçe yavaşlar.
1. Tank dolu ve pompa basıncı sıvı basıncından büyüktür...

- Tank tamamen dolduğu anda pompa basıncı tankın içindeki sıvı basıncından büyükse oluşan basınç farkı tank çeperlerini zorlamaya başlar. Basınç farkı tank çeperinin dayanabileceği şiddette olursa sıvı akışı durur ve denge sağlanır, eğer çeperler basınç farkına dayanamıyorsa bu zorlama bir süre sonra çeperleri deforme eder ve sonuçta tank patlar.
- Çözüm: Pompa basıncını dengelemesi için daha yüksek bir sıvı tankına ihtiyaç vardır. Eğer tankın aldığı sıvı miktarı değişmeyecekse taban alanı daha küçük ancak boyu daha uzun bir tank tercih edilir. Böylece sıvı miktarı sabit kalır, basınç dengelenir ve tank çeperleri zorlanmaz.
- Yani, kondansatörler çalışma gerilimlerinin üzerinde bir gerilime maruz bırakılmamalıdır. Yalıtkan malzeme dayanamayacağı gerilimler altında deforme olur ve patlamaya yol açar. Bunun yerine daha yüksek gerilimlere dayanabilen ve kullanılan yük miktarında değişim olmaması için kapasitesi nispeten düşük kondansatörler tercih edilir.

2. Tank dolu, pompa basıncı ile sıvı basıncı eşit, ancak sıvı miktarı az...
- Tank tamamen dolduğu anda sıvı basıncı pompa basıncını dengeliyorsa, net basınç sıfır olur ve tank çeperlerinde bir zorlanma olmaz. Ancak sıvı miktarının az olması, sıvının kullanılırken daha önceden bitmesine ve işte verimsizliğe yol açar.
- Çözüm: Basınç dengesinin bozulmaması amacıyla sıvı tankının yüksekliği değiştirilmez, ancak taban alanı artırılarak aynı basınç değerinde daha fazla sıvı depolanabilir. Taban alanının artışıyla tank hacmi ve maliyet artar.
- Yani, nominal gerilimde çalıştırılan bir kondansatörün daha büyük elektriksel yükü depolaması ve daha uzun süre devreye enerji sağlaması için hidrolikte taban alanı eşdeğeri olan kapasitesi artırılır. Yandaki resimde sıvı tankının hacmi ve iş görme süresi iki katına çıktığı gibi, kapasitesi iki katına çıkan kondansatör de iki kat yük depolar ve iki kat süre dayanım gösterir.
3. Pompa basıncı ile sıvı basıncı eşit, ancak sıvı tankı tamamen dolmadı...
- Tank tamamen dolmadan içindeki sıvı basıncı pompa basıncına eşit olursa sıvı akışı durur ve tankın üstünde boş kısımlar kalır. Bu durum eldeki tankın gereğinden büyük olduğunu gösterir ve fazladan maliyet getirir.
- Çözüm: Sıvı basıncının pompa basıncını dengelediği yükseklikte bir sıvı tankı tercih edilir. Sıvı tankının gereğinden büyük olması verimsiz kullanıma örnektir.
- Yani, kondansatörler ya tam uygulanacak gerilim değerine ya da aşırı olmayacak şekilde yüksek gerilim değerlerine göre tercih edilir. Uygulanan gerilimin çok üstünde olan çalışma gerilimi, maliyeti fazla olan kondansatör anlamına gelir ve elemanın verimsiz kullanılmasıdır.
Çift yönlü sıvı akışı[değiştir | kaynağı değiştir]
Hidrolikte AC kaynak, sıvı akış yönü, hızı ve basıncı belli bir frekansa göre değişen pompa olarak düşünülebilir. Kondansatör eşdeğeri olan sıvı tankına bağlanmış bir pompadan, periyodun bir yarısında tanka sıvı verildiği diğer yarısında tanktan sıvı çekildiği, basınç değişiminin de sinüsoidal şekilde olduğu benzetimi ile AC kaynağa bağlanmış bir kondansatör gözde daha kolay canlanır. Sıvı akış yönünün değiştiği sistemlerde sıvı tankı sürekli dolup boşalma hareketi yapar, sıvı akışı durmaz ancak sıvı akışına karşı bir direnç oluşur. Bu direncin bağlı olduğu büyüklükler şöyle sıralanabilir.
- Frekans: Tankın dolması için bir süre gerekir, bu süre tankın hacmine bağlıdır. Frekansın büyük olması periyotun küçülmesini gerektirir. Periyotun yarısında tanka sıvı dolduğu diğer yarısında da çekildiği göz önüne alınırsa, periyot küçüldükçe kısa sürede tanka dolan sıvı miktarı daha da düşer, tank tamamen dolup pompayı tıkama işlemini yapamaz ve tankın direnci azalır. Yani, frekansın artması sıvı tankında olduğu gibi kondansatörlerde de dirence ters orantılı etki yapar.
- Taban alanı: Taban alanının genişlemesi, aynı miktarda sıvının daha az yükseklikte ancak daha geniş yüzeyde birikmesi anlamına gelir. Sıvı tankında biriken sıvının yüksekliğinin azalması da pompaya tanktan uygulanan basınç değerinde azalmaya yol açar, böylece sıvı daha kolayca tanka dolar ve tankın direnci azalır. Yani, taban alanının büyümesi sıvı tankının direncini azalttığı gibi kondansatörlerde de kapasite değerindeki artış kondansatör direncini azaltır ve ters orantı söz konusudur.
Üstteki formülasyon bir sıvı tankının basıncı sinüsoidal şekilde değişen pompadan sıvı girişine gösterdiği direncin nelere bağlı olduğunu ifade eder. Hidrolikteki eşdeğerleriyle yer değiştirdiğinde ise kondansatörün AC kaynakta elektron ve akım akışına gösterdiği direnç elde edilir. Formülasyonlar arasındaki tek fark olan çarpanı, kondansatörün AC direnci ifadesinde açısal frekansın kullanılmasından kaynaklanır. Kapasite değeri ve çalışma frekansının artması kondansatör direncinin düşmesine neden olur.
Sıvı pompası basıncının sinüsoidal şekilde olması, bir periyotun yarısında tanka sıvı gönderip diğer yarısında sıvı çektiği anlamına gelir. Sıvı gönderme sürecinin sonlarına doğru sinüsoidal grafikten kaynaklanan nedenle, sıvı tanka doğru itilmesine karşın pompa basıncı oldukça düşer ve sıfıra yaklaşır. Ancak tankta birikmiş sıvının basıncı pompa basıncından büyük hale gelir ve basınç farkı pompa sıvıyı tanka doğru itmesine karşın negatif çıkar. Yani, pompa basıncı tanka doğrudur ancak sıvı akışı tanktan dışarıya doğru gerçekleşir, dolayısıyla sıvı akışı faz olarak pompa basıncından ileridedir. Kondansatör benzetiminde eşdeğer büyüklükler kullanılırsa akım fazörü gerilim fazöründen ileridedir denilir.
Matematiksel analizi[değiştir | kaynağı değiştir]
Kapasite birimi[değiştir | kaynağı değiştir]
Kondansatörler, elektrik yükünü yalıtkan malzemesinin içerisinde elektrik alanı olarak depolar. Kapasite , bir kondansatörün yük depolayabilme yeteneği olarak tanımlanır ve birimi (Michael Faraday'ın anısına) Farad' olarak belirlenmiştir. Uluslararası MKS birim sisteminde , uçları arasına gerilim uygulandığında elektron depolayabilen kondansatörün kapasitesine eşittir. Matematiksel formdaki ifadesi ise aşağıdadır.
Kondansatör - sıvı tankı benzetiminde elektronun karşılığının sıvı damlası olduğu göz önüne alınırsa kapasitenin çok büyük bir değer olduğu anlaşılır. Bundan dolayı uygulamada biriminin alt katları daha yaygındır. Kapasite değeri metal tabakaların alanına ve yalıtkan malzemenin dielektrik katsayısına doğru orantılı, metaller arası uzaklığa ters orantılı bağlıdır.
Sıvı tankı benzetiminde de belirtildiği üzere kapasite, bir kondansatörün bir kaynağı ne kadar besleyebileceğinin de ölçütüdür, kapasite değeri arttıkça kondansatörün yükü besleyebileceği süre de artar.
Zaman domeininde ifadesi[değiştir | kaynağı değiştir]
Kondansatörün uçları arasına bir gerilim farkı uygulandığı zaman, devreden akım geçer. Eğer kondansatörün uçları arasında gerilim değişikliği olmazsa bir süre sonra kondansatör dolar ve akım geçirmemeye başlar. Gerilimde bırakılıp dolmuş ve akım geçirmeyen bir kondansatörün uçları arasındaki gerilim değiştirildiği anda ise devreden yeniden akım geçmeye başlar. Yani kondansatör akımı, uçları arasına uygulanan gerilimin değişimine bağlıdır. Bu durum aşağıdaki gibi gösterilir.
Bu ifadenin pratik olarak anlamları şöyle sıralanabilir:
- Kondansatörden akım geçebilmesinin tek şartı, uçları arasındaki gerilim farkının değişmesidir. Bu gerilim farkı aynı kaldığı müddetçe, kondansatör depoladığı yükü boşaltmaz, tıkama görevi görüp devreden akım geçmesine engel olur. Matematiksel ifadede de görüldüğü gibi, gerilim değişmediği zaman türev ifadesi olarak dışarı çıkar ve akımın da olmasına neden olur, böylece devreden akım akmaz.
- Gerilim kesinlikle bir an içinde büyük değişikliğe uğramamalıdır. Birden artan veya azalan gerilim, türev ifadesinin çok büyümesine, böylece darbe akımı oluşmasına yol açar. Yani gerilimin ani büyük değişimi akımın oldukça artmasına, bu da kondansatörün zarar görüp deforme olmasına neden olur.
Aşağıdaki ifade ise bize kondansatör geriliminin, akım cinsinden değerini söyler. Akımın integrali, kondansatörde depolanan elektrik yükünü verdiğinden, kapasiteye oranı bize uçlar arasındaki gerilimi verir.
| |
Frekans domeininde ifadesi[değiştir | kaynağı değiştir]

Bir devre elemanının ifadesi, eğer sinüsoidal bir kaynağa bağlanırsa frekans domeninde yazılabilir. Bu hesaplamalarda, özellikle de türev ifadesinin yok edilmesinde çok kolaylık sağlayacaktır. Bunun için ise fazör yöntemini kullanacağız. Gerilim ve akım fazörleri aşağıdaki gibidir ve büyük harflerle belirtilirler.
Devrede kondansatör[değiştir | kaynağı değiştir]
Seri bağlama[değiştir | kaynağı değiştir]

Kondansatörlerin seri bağlanmasında öncelikle uçların doğru bağlanıp bağlanmamış olması sonrasında da kondansatörlerin yüklü olup olmaması göz önüne alınır. Her bir kondansatörün ucu sonraki kondansatörün ucuna bağlandığında seri bağlama sağlanmış olur. Yandaki resimde düzgün olarak seri bağlanmış 3 adet kondansatör bulunmaktadır. Kondansatörler seri bağlandığı zaman, kaynak akımı her bir kondansatörden geçen akıma eşit olur, kaynak gerilimi ise her bir kondansatörün gerilimlerinin toplamı olur.
Zaman domeninde hesap[değiştir | kaynağı değiştir]
Frekans domeninde hesap[değiştir | kaynağı değiştir]
Paralel bağlama[değiştir | kaynağı değiştir]

Paralel bağlı elemanların uçları aynı noktaya, yine uçları da aynı noktaya bağlanır. Kondansatörlerin paralel bağlanmış şekli yandadır. Paralel bağlamada her bir kondansatörün gerilimi kaynak gerilimine eşittir, kaynak akımı ise her bir kondansatöre giden akımların toplamıdır.
Zaman domeninde hesap[değiştir | kaynağı değiştir]
Frekans domeninde hesap[değiştir | kaynağı değiştir]
Kondansatörde güç & enerji[değiştir | kaynağı değiştir]
Yüklü kondansatörde depolanan enerji[değiştir | kaynağı değiştir]
Kondansatörün uçları arasına gerilim uygulandığı anda plakalar arasındaki yalıtkan malzemenin elektronları kutuplanırlar. Elektronlar tarafa doğru yönlenmeye çalışırken, uç elektronları kendinden uzaklaştırır ve yalıtkan malzemenin kutuplanması böylece sağlanmış olur. Kutuplaşmanın ve gerilim farkının olduğu bir bölgede elektrik alanın varlığından bahsedebilir. Kondansatörde depolanan enerji, pil tarafından yapılan iş yoluyla bulunabilir. Bir yükünün noktasından noktasına taşınmasıyla birlikte, kondansatörün kapasitesi 'ye göre bir gerilimi oluşur.
Aşağıdaki ifade oldukça küçük bir yükünün noktasından noktasına taşınması sırasında yapılan çok küçük işi gösterir.
Aşağıdaki formül ise yük miktarını 'dan 'ya entegre ederek, kapasitesi olan bir kondansatörde geriliminde kadar yükü depolamak için gereken enerji miktarını verir.
Kondansatörde Depolanan Enerji
Sinüsoidal kaynakta anlık güç[değiştir | kaynağı değiştir]
Sinüsoidal bir kaynakta anlık güç ifadesi aşağıdaki gibi bulunmuştur. Formülasyonda simge kalabalığı olmaması açısından faz farkı olarak tanımlanmıştır.
Kapasitif yükün anlık gücü[değiştir | kaynağı değiştir]
Kapasitif yük, empedansının sanal kısmında kapasitif reaktansın etkisinin baskın olduğu yüktür. Kapasitif yüklerde sanal kısım değer alır. Faz diyagramı çizildiğinde de kapasitif reaktansın etkisi sebebiyle sanal kısım aşağı doğru yönlenmiştir. Bunun nedeni, kapasitif yüklerde akım fazörünün gerilim fazörüne göre önden gitmesidir. Dolayısıyla faz farkı olarak tanımlanan ifadesi negatif değer alır.
Anlık gücün genel ifadesi her türlü yük için geçerlidir. Kapasitif yüklerde faz farkı negatif olduğundan bu durum ele alınabilir, yerine koyulursa üstteki anlık güç ifadesi az da olsa değişikliğe uğrar. Faz farkının işareti hesaba katılınca, ve trigonometrik eşitliklerinden anlık güç aşağıdaki hali alır.
Genel anlık güç ifadesinden farklı olarak kapasitif yüklü bir devrede güç ifadesinde, reaktif gücün işareti olur. Reaktif gücün pozitif olmasının anlamı şudur: Kapasitif bir yükte reaktif güç pozitif çıkar, kondansatör bu sebeple bir reaktif güç depolama elemanı olarak görülebilir. İlerleyen zamanla birlikte kondansatör, reaktif gücü kendinde toplamaktadır. Kapasitif yükler saf kapasitif yüklerden farklı olarak bir direnç (resistans) kısmı da bulundurduklarından devrede aktif güç harcaması da yaparlar. Bu aktif güç tamamen dirençler üzerinde harcanır, kondansatörde depolanan ise tamamen reaktif güçtür. [14]
Saf kapasitif yükün anlık gücü[değiştir | kaynağı değiştir]
Saf kapasitif yükte, kapasitif yükten farklı olarak resistif kısım bulunmaz. En basitinden bu, üzerine kondansatör haricinde hiçbir devre elemanı bağlı olmayan bir devre olarak düşünebilir. Dolayısıyla bulanacak anlık güç, bir kondansatörün sinüsoidal devreye bağlandığında depolayabileceği reaktif güce eşit olur. Saf kapasitif yüklerde akım fazörü gerilim fazörüne göre kadar önde ilerler. Yani faz farkı ifadesi değerini alır. Bu değer, anlık güç ifadesinin içinde bulunan faz farkı kısmına yerleştirip aşağıdaki formülasyona ulaşılır.
Saf kapasitif yükte anlık güç ifadesi oldukça basitleşir ve formülde sadece reaktif güç kısmı kalır. Bu formülasyonun anlattığı şudur: Saf kapasitif bir yükte reaktif güç pozitif çıkar ve kondansatör bir reaktif güç depolayıcısı olarak çalışır. Devrede direnç bulunmadığından aktif güç harcanması olmaz ve anlık güç tamamen reaktif güçten oluşur. Yani reaktif güç alabileceği en büyük değerini alır ve kondansatör bu gücü depolama yönünde çalışır.
Kaydedilen elektriksel yükün bosalmasi[değiştir | kaynağı değiştir]
Kondansatörler akü olarak da kullanılmaktadırlar, çünkü gerilimi yavaş şekilde azalabilecek şekilde devrelere takılabilirler.
Kaydedilen elektriksel yük elektrik akımı olarak boşalır. Dolayısıyla:
ve de
ile
Yani:
Bu diferansiyel denklemin çözümü dir.
Böylece gerilim dirençle oynanarak yavaş veya hızlı şekilde boşaltılabilir.
DC akım analizi[değiştir | kaynağı değiştir]
DC analizin matematiksel anlamı[değiştir | kaynağı değiştir]
Kondansatör bir DC kaynağına (örneğin pil) bağlandığında elektron bazında gerçekleşen olaylar şöyledir;
- Kondansatörün pilin (-) ucuna bağlı olan ucu, pilin ürettiği elektronları kabul eder ve kendine çeker.
- Kondansatörün pilin (+) ucuna bağlı olan ucu, elektronlarını pile doğru verir.[15]
Kondansatörün uçları arasında oluşan bu elektron sayıları farkı, uçlar arasında gerilim farkına yol açar. Bu gerilim farkı, kondansatör uçlarına bağlanan DC kaynağın veya pilin gerilimine eşittir. Kondansatör DC kaynağa bağlandığı zaman kapasitesini doldurana dek devreden bir akım geçer. Bu akımın analizi, DC gerilime bağlanmış kondansatör ve lambadan oluşan bir devre üzerinden yapılabilir.

Son durumda kondansatör üzerinde oluşan gerilim farkı kaynağa eşit hale gelir ve elektron akışı durur.
İçinde yük barındırmayan bir kondansatörün başlangıç anı gerilimi olur. Bu kondansatörün ucuna doğru gerilimi uygulandığı zaman devrede oluşan gerilim farkı aşağıdaki gibi ifade edilir.
Bu gerilim farkının önündeki dirençler ise kondansatörün iç direnci ile lambanın direncidir. Lamba direncine , kondansatör iç direncine de adı verilir.
Devre tamamlandığı ilk anda elektronlar akmaya başlar ve hızlıca kondansatörün kutuplanmasını sağlarlar. Bağlanmanın gerçekleştirildiği ilk an olan anında elektronlar harekete geçerler, bu öyle kısa bir an sayılır ki kondansatörde o ana kadar hiç yük birikmez. Yani gerilim farkı hâlâ DC kaynağın gerilimine eşittir. Bu anda akımın değeri aşağıdaki gibi elde edilir.
DC gerilime bağlı bir kondansatör ve lamba devresinin üzerinden geçen akımın alabileceği en yüksek değer budur. Çünkü zaman ilerledikçe kondansatör dolmaya başlar ve kutuplandıkça DC kaynağa ters bir DC kaynak gibi davranır. Zamanın sonsuza doğru gittiği varsayılırsa, kondansatör kaynağın değerinde ve kaynağa ters bağlı bir DC kaynak haline gelir. Yeterli zaman geçtikten sonra haline gelir ve devrede oluşan gerilim farkı olur.

Açıktır ki, gerilim farkının oluşmadığı bir devreden akım geçmez. Kondansatör başlangıç anında boştur ve yük biriktirmeye başlar, devreden akım geçer; dolduktan sonra ise bir pil gibi davranır ve devreyi tıkar, akım akmasını engeller. Bu iki zaman aralığında ise akım değişimi şöyle incelenir. İlk anda olan kondansatör gerilimi, hızlıca kutuplaşmanın sağlanmasıyla birlikte, ulaşacağı değer olan gerilimine doğru artış gösterir. Elektronların hareketi olduğu sürece kondansatörün gerilimi artar, devrenin net gerilim farkı zaman ilerledikçe düşer. Buna bağlı olarak da akım değeri başlangıç değerinden sürekli bir azalma gösterir. Nitekim zaman yeteri kadar ilerledikten sonra da akım olur. Akımdaki bu düşüşün grafiği çıkarıldığı zaman azalmanın doğal logaritmik bir şekilde gerçekleştiği görülmektedir. Kutuplanması sağlanmış bir kondansatör devreden sökülüp kullanılabilir. Bu anda artık kondansatörün başlangıç gerilimi olarak hesaplamaya katılır.
DC analizin pratik anlamı[değiştir | kaynağı değiştir]

DC kaynak, bir adet lamba ve kondansatör devresinin pratik hayattaki incelemesi yandaki animasyonda görülür. Kondansatör ilk anda yüksüzdür, bir DC kaynağı olan pile bağlanırsa yük depolar, bu arada üzerinden zamanla doğal logaritmik azalan bir akım geçer. Tam dolu haldeki kondansatör bir anahtar yardımıyla pilden ayrılır ve lambaya bağlanır. Kondansatör bu haliyle bir DC kaynak gibi davranır ve lambaya bağlandığının ilk anında akım en yüksek değerinden akmaya başlar. Yani lamba en parlak halindedir. Lamba yanmaya devam ettikçe kondansatörün depoladığı yük düşer ve lamba parlaklığı azalır. Depolanan yük tükendiğinde ise lamba tamamen söner. Lambanın yanma süresinin artırılması için, daha yüksek kapasiteli bir kondansatöre ihtiyaç olur.
Örneğin 5 V ile çalışan bir lambanın saniyede kullanacağı elektrik yükünün değeri 1 nanoFarad kabul edilirse, bu lambanın ucuna 5 V çalışma gerilimine sahip 10 nanoFarad 'lık yükü depolamış bir kondansatör bağlandığında, lambamız 10 saniye boyunca yanar. Bu süreyi artırmak için kondansatörün kapasitesi artırılır, ancak kondansatörün boyutları ve maliyeti de artar.
DC kaynak, kondansatör ve lamba eğer seri olarak bağlanırsa, empedans değerine göre devreden bir akım akmaya başlar, bu akımın alabileceği en yüksek değerdir. Çünkü henüz kondansatör kutuplanmaz ve gerilim biriktirmez. DC kaynağa bağlı bir kondansatörün karakteristiğine göre kutuplanmaya başlayan kondansatör, ters bağlı bir DC kaynak gibi davranır ve lambanın uçları arasındaki net gerilimin düşmesine neden olur. Lambanın parlaklığı doğal logaritmik olarak azalır. Kondansatör kutuplanmasını tamamladığında ise, devrenin net gerilimi sıfır olur ve lamba tamamen söner.
Kondansatörün çalışma gerilimine uygun değerde bir DC gerilime tabi tutulmasına dikkat edilmelidir. Anma gerilimdeğerinin çok üstünde bir gerilime tabi tutulan plakalar arasındaki yalıtkan malzeme deforme olur ve üzerinden akım kaçırmaya başlar. Bu kaçak akımı çok büyürse kondansatörün kapasitesine göre büyüklüğü değişen bir patlama gerçekleşir. Çünkü gerilim farkının önünde olan kondansatör direnci oldukça küçüktür, bu da akımın büyümesine neden olur.
AC akım analizi[değiştir | kaynağı değiştir]
AC analizin matematiksel anlamı[değiştir | kaynağı değiştir]
Kondansatörün DC akıma göre davranışı, AC akımda değişiklik gösterir. AC akım, gerilim ve akım yönünün belli bir frekansa göre yön değiştirdiği elektrik enerjisidir. Gerilimin yönü ve genliği sürekli değiştiğinden kondansatörde depolanan elektrik yükü ve uçları arasındaki gerilim de sürekli değişim içindedir. Kondansatör dolup boşalma hareketini frekans sıklığında gerçekleştirir. Kondansatör bağlı bulunan bir AC devrede, akım bir süre sonra kesilmez. Sonuç olarak: AC devredeki kondansatör, akım akışına karşı bir engel oluşturmaz, ancak bir direnç gösterir denilebilir. Kondansatörün gösterdiği bu dirence Kapasitif Reaktans denir. Kapasitif reaktans, ile gösterilir, birimi dirençle aynı olup Ohm'dur.
| Kapasitif Reaktans |
Açısal Frekans |
Frekans | Kapasite |
Bu ifadeden hareketle kondansatörün kapasitif reaktansının; kapasitesi ve frekansı ile ters orantılı olduğu söylenebilir. Kondansatörün kapasitesi ve çalışma frekansı arttıkça kapasitif reaktansı, diğer bir deyimle direnci azalır.
Kondansatörün AC akıma karşı gösterdiği bu direnç, resistif (omik - saf direnç) dirençten farklıdır. Saf dirençte gerilim farkı ile akım arasında direnç değeri kadar bir oran olmasına rağmen, kondansatör ve endüktans gibi değişken ifadelere sahip elemanların dahil olduğu bir devrede bu oran değişir. Kondansatör AC akımda dirence dolaylı yönden etki etmektedir. Açıklamak için empedans kavramını tanımlanır.


Empedans[değiştir | kaynağı değiştir]
Empedans yukarıdaki gibi tanımlanırken saf direnç eşdeğerini, reaktansın eşdeğerini belirtir. Kondansatörün ve kapasitif bir sistemin reaktansı 'dir. Dolayısıyla empedansın sanal kısmı frekans domeni ifadesine göre aşağıdaki gibi olur.
Bir direnç ve bir kondansatörün bağlı olduğu devre göz önüne alındığında empedans, aşağıdaki gibi olur.
Empedansın sanal kısmında işaret 'ye dönüştü. Bu da yandaki empedans diyagramında olduğu gibi kapasitif reaktansın ters yönde dönmesine neden olur. Dolayısıyla, kondansatör empedansının faz açısı negatif yönde çıkar. Aşağıdaki grafikten de kapasitif bir yükün empedansının fazör diyagramı görülür.
Bu ifadeden anlaşılan, gerilimin faz değerinin, akımla empedansın faz değerlerinin toplamı olduğudur. Kapasitif devrede empedansın faz değeri negatif olduğundan aşağıdaki eşitlikler çıkartılır.
Son ifade akımın faz açısının gerilimin faz açısından büyük olduğunu ifade etmektedir. Yani akım fazörü, gerilim fazörüne göre önde ilerler. Kapasitif devrelerde akım gerilimden ileridedir ve empedansın sanal kısmı negatif değer alır.
Faz farkı[değiştir | kaynağı değiştir]
AC devrelerinde reaktif güç devreye girer ve hesabı için faz farkına ihtiyaç vardır. Kondansatör plakaları arasında depoladığı elektrik enerjisini kaynak kesildikten sonra devreye verdiğinden faz kayması oluşturur. Kapasitif devrelerde empedansın sanal kısmı negatif değer alır, bu da empedansın faz değerinin negatif olması anlamına gelir.

akım – gerilim grafiği.
Akım - Gerilim
Akım – Gerilim – Empedans arasındaki ilişki kullanılır;
Bu ifadeler, gerilimin faz açısının, akımla empedansın faz açılarının toplamına eşit olduğunu belirtir. Kapasitif devrede empedansın faz değeri negatif olduğundan, aşağıdaki eşitlikler çıkarılır.
Grafikte akım ile gerilim grafiklerinin ekseni kestiği noktalar görülüyor ve akım grafiği x eksenini daha önce keser. Yani akım faz olarak gerilimden daha ileridir. Bu da tanıma göre kapasitif yüklerde faz farkı açısının negatif olduğunu ifade eder.
Faz farkı gözlem yoluyla da anlaşılabilir; kondansatör, üzerine gerilim uygulandığı anda dolmaya başlar, frekans değerine göre üzerinden akım geçirme düzeyi artar. Kapasitif bir devreye herhangi bir anda bakıldığında, bazı anlarda gerilim olmasına rağmen akımın hâlâ akmaya devam ettiği görülür. Çünkü kaynak kesildiğinde bile, kondansatör depoladığı yüklerle devreden bir süre akım geçmesini sağlar. Bunlar faz farkının varlığına işarettir.
Reaktif güç[değiştir | kaynağı değiştir]
Reaktif güç elektriksel güçte görünür gcün bir bileşeni olup iş yapabilme ve işe dönüştürülebilme özelliği yoktur. Bu güç, kondansatörlerde plakalar arasında elektriksel alan olarak saklanır. Kaynak kapandığında ise devreye geri verilir. Anlık gücün yukarıda bulunan tanımında içinde faktörünün bulunduğu kısım bize reaktif güç değerini verir. Reaktif gücün frekansı da normal frekanstan farklıdır, iki katına çıkar.
Güç ifadesi, elemandan geçen akımla elemanın uçları arasındaki gerilimin çarpımından oluşur. Empedans kavramının verdiği bilgiler eşiğinde aşağıdaki eşitlikler sağlanır. Akım fazörünün üstündeki yıldız , fazörün transpozesinin alındığını, daha basit anlamıyla genliğinin sabit kalması şartıyla faz açısının terse dönüp işaret almasını anlatır. Ayrıca fazörlerin altında bulunan ifadesi de fazörlerin efektif yani etkin değerlerinin alındığını gösterir. Sinüsoidal bir dalgada efektif değer, genliğin 2'nin kareköküne bölünmüş halidir. Matematiksel olarak aşağıdaki ifadeler kullanılabilir.
Bu formüller ışığında kondansatörde depolanan reaktif güç aşağıdaki gibi bulunur.
AC analizin pratik anlamı[değiştir | kaynağı değiştir]
Kondansatör her ne kadar direnç gibi pasif, yani kontrolsüz elemanlardan da olsa dirence göre farklılıklar taşır. Matematiksel ifadesi direnç gibi doğru orantılı değildir, türev ifadesi içerir. Kondansatör akımının akması, zaman domeni ifadesinden anlaşıldığı gibi, kondansatörün uçları arasındaki gerilimin değişmesine bağlıdır. Alternatif akımda kaynak gerilimi sürekli değişir, kondansatöre uygulanan gerilim değeri de değişime uğrar. Bu da kondansatörden sürekli akım geçmesini sağlar.
Kondansatör AC akımın geçmesini engellemez. Direnç elemanı gibi olmasa da akıma karşı bir tepki gösterir, direnç uygular. Omik dirençten farklı olarak akımın hem değerini düşürür, hem de fazının gerilime göre kaymasına neden olur. Kondansatörün AC gerilime karşı koyma eşdeğerine kapasitif reaktans adı verilir. Kapasitif reaktans, kaynak frekansı ve kondansatör kapasitesine bağlıdır. Frekans ve kapasite yükseldikçe reaktans düşer. Reaktansın düşmesi;
- empedansta direnç etkisinin artması
- fazör diyagramında sanal kısmın kısalıp empedansın dirence yani gerçel kısma doğru yaklaşması
- faz farkının düşmesi, akım ve gerilim fazörlerinin birbirine yaklaşması anlamlarına gelir. Reaktansın yükselmesi ise bu sıralananlara ters yönde etki yapar.
Empedans diyagramı incelendiğinde görülür ki, kapasitif yüklerde empedansın sanal kısmı negatif, direncin yönü sürekli pozitif yönde olur. Reaktans negatif yönde olduğundan bu iki fazörün bileşiminin açı değeri negatif çıkar. Empedansın açısı kapasitif yüklerde negatif değer alır ve dolayısıyla akım fazörü gerilim fazörünün önünden ilerler. Kondansatör, çalışmaya başladığında sürekli olarak dolup boşalma hareketi yapar, belli bir yerde kaynak akımı kesilirse kondansatör depolamış olduğu yükleri devreye verir ve kısa süre de olsa akım geçmesini sağlar. Yani akım fazörü gerilim fazöründen ilerdedir denir.
Kondansatör reaktif güç depolayan bir elemandır. Reaktif güç işe dönüştürülmemesine rağmen motorlar endüktif ve bobin yapısında olduğundan çalışmaya başlamaları için bir manyetik alana ve reaktif güce ihtiyaç duyarlar, endüktif devrelerin çalışması için gereken reaktif güç de kondansatörlerden karşılanır. Ancak şebeke durumundan bakarsak reaktif gücün ihtiyaçtan fazla bulunmasının istenmeyen bir durum olduğu unutulmamalıdır. Bunun için kompanzasyon yapılır ve reaktif gücün düşürülmesi yoluna gidilir.
Kullanım ve uygulama alanları[değiştir | kaynağı değiştir]
Kondansatörün matematiksel ifadeleri ve pratik anlamda bu ifadelerin ne anlamlara geldiği bilgilerinin ışığında, kondansatörler çeşitli amaçlarla birçok kullanım alanı bulur. Bu kullanım alanlarını belirleyen özellikler;
- elektrik enerjisini plakaları arasındaki depolayabilmek,
- kısa devre anında bu enerjiyi çok hızlı boşaltabilmek,
- faz kayması oluşturmak ve reaktif gücü depolayabilmek olarak sıralanabilir.
Aşağıdaki liste hangi uygulamanın ne kadar kapasiteli kondansatörlerle gerçekleştirildiği ve bu kondansatörlerin ne gibi özelliklere sahip olması gerektiği hakkında bilgi sunar.[16]
| Uygulama | Kapasite aralığı | Tolerans gereksinimi | Kaçak akım tahammülü | Kararlılık gereksinimi | Parazit tahammülü |
|---|---|---|---|---|---|
| Filtreleme | 1 - 100 pF | Yüksek | Düşük | Kesinlikle | Düşük |
| AC/DC Doğrultma | 1 - 10 nF | Yüksek | Düşük | Çok Yüksek | Yüksek |
| Dekuplajlama | 1 - 100 nF | Düşük | Yüksek | Düşük | Çok Düşük |
| Enerji Depolama | 1 µF ve üstü | Düşük | Yüksek | Düşük | Düşük |



Enerji depolama[değiştir | kaynağı değiştir]
Kondansatöre bir DC kaynak bağlandığı zaman, kısa sürede yükü depolar ve dolar. Bu şekilde devreden ayrılan bir kondansatör yüklüdür ve plakaları arasında bir gerilim değeri okunur. Bu şekliyle kondansatörler bir pile benzetilebilir. İçindeki yükü ise kendisine bağlanan direnç değerine göre belli bir sürede boşaltan kondansatörler, devreye bağlandığı zaman kısa süre içinde yüklerini tüketirler, çünkü içlerindeki yük pile göre hem azdır hem de yeni yük üretimi yapamaz. Kondansatöre kısa devre yapıldığında bu yükün kıvılcım çıkartacak derecede hızlı aktığı görülür. Hem enerjiyi depolama hem de yükü aniden devreye sokma özelliklerinden dolayı, kaynağın devre dışı kalacağı durumlarda ve ani yük akışına ihtiyaç olan alanlarda kondansatörler kullanılabilir.
Fotoğraf makinesi flaşlarının çalışması için enerji depolayan araçlar kondansatörlerdir. Flaşa bağlanmış olan kondansatör önce pil tarafından doldurulur ardından çekim anında devreye sokulur ve depolanmış yüksek enerji bir anda boşaltılır, böylece anlık olarak yüksek aydınlık elde edilmiş olur. Flaşın biriktirdiği yüksek enerjiyi bir anda harcaması kondansatör sayesinde olmaktadır. Kondansatörün aniden boşalması flaş ışığının parlak olmasını sağlar.[17]
Kondansatörler, elektronik alet herhangi bir sebeple kaynaktan ayrılırsa aletin bir süre daha işlev görmesini de sağlar. Buna örnek olarak hoparlörler verilebilir. Hoparlörlerin besleme devresinde bulunan kondansatörler kaynak gerilimi kesildiği zaman birkaç saniyeliğine de olsa höparlörün çalışmasını ve ses kaybı olmamasını sağlarlar. Hoparlörün çalıştığı süre boyunca depolanan kondansatör, kaynağın kesintiye uğramasının ardından depoladığı yükü hoparlöre verir ve böylece ses bir süreliğine kesilmez. Fişten çekilen hoparlörden hâlâ ses gelmesinin nedeni budur. Bu kullanım şekli daha da genişletilebilir, farklı farklı kullanım alanları bulunabilir.
Kondansatör, kendisini besleyen kaynak tükendiği zaman hafızasındaki bilgiyi kaybeden elektronik aletler için geçici de olsa çözüm oluşturur. Dijital kol saatleri, bazı bilgisayar parçaları, cep telefonları bu tür aletlere örnek olarak verilebilir. Dijital saatler ve cep telefonlarında bulunan kondansatör, pil tükendiği zaman devreye girer ve özellikle saat ve bazı önemli bilgilerin kaybolmaması için yüklerini harcarlar. Kondansatör belli bir süre sonra yeniden depolanmadığından boşalacaktır ve bulunan çözüm geçici olacaktır. Bazı cep telefonlarının pillerinin birkaç saniyeliğine çıkarılıp geri takıldığında açılışta saati hatırlaması, daha uzun süreli pilsiz bırakmada ise açılışta saati yeniden sormasının sebebi de budur. Çünkü kondansatör o hafızayı sadece birkaç saniyeliğine tutacak şekilde tasarlanmıştır.
Kondansatör ani yük boşalmaları yapabildiğinden laboratuvar ortamında deney ve yapay yıldırım oluşturma amacıyla da kullanılır. Bir yapay yıldırımda aktarılan yük miktarı ve oluşan gerilim o kadar büyüktür ki, bu yükü depolamak için metrelerce uzunlukta büyük kondansatör blokları ve bu kondansatörleri doldurmak için dakikalar gerekmektedir. Depolanan enerji bir anda kısa devre edilir ve bir noktaya hedeflendirilir, böylece yapay bir yıldırım oluşturulabilir.
Reaktif güç depolama ve faz kaydırma[değiştir | kaynağı değiştir]
Anlık güç ifadesinde de anlatıldığı üzere kondansatörler aktif güç harcamazlar ve reaktif güç depolayıcı olarak çalışırlar. Endüktif devreler ise çalışmalarının başlangıcı için reaktif güce ihtiyaç duyarlar ve çalışırken reaktif güç oluştururlar. Kondansatörler reaktif güç depolarken endüktanslar da çalışmak için reaktif güç harcıyorlar. Bu harcayacakları güç de kondansatörler tarafından sağlanabilir. Ayrıca endüktif devrelerin faz kayması akımın geri kalması yönündeyken, kapasitif devrelerin faz kayması akımın önde gitmesi yönündedir. Bu da faz açısının ayarlanması için bize olanak sunar.
Motorlara yol verme[değiştir | kaynağı değiştir]

Elektrik makineleri veya daha bilinen adıyla motorlar büyük bobin sarımlarından oluştuğundan endüktif devrelere sahiptirler. Endüktif devrelerin anlık güçlerinin ifadeleri çıkarıldığında görülecektir ki endüktanslar harekete geçmeleri için reaktif güç harcayıp çevrelerinde manyetik alan oluştururlar. Bu reaktif güç şebekeden de çekilebilir. Ancak birçok fabrikanın, birçok motorun ve endüktif devrenin bulunduğu bir bölgede çekilen reaktif güç verimin oldukça aşağı düşmesine neden olacaktır. Bunun için motorların devrelerine reaktif güç yüklü kondansatörler bağlanır ve motora yol verilmesi yani motorun harekete geçirilebilmesi için gereken reaktif güç bu kondansatörlerden sağlanır. Bu kondansatörler elektronik devrelerde kullanılan kondansatörlere göre fiziksel olarak oldukça büyüktür. Çünkü motorlar 220 veya 380 Volt ile çalışırlar ve fazla miktarda reaktif güce ihtiyaçları vardır, bunu depolayacak kondansatörler de tabii ki büyük olacaktır.
Kompanzasyon[değiştir | kaynağı değiştir]

Reaktif güç ile aktif gücün bileşiminden oluşan görünür güçte, aktif gücün maksimum hale getirilip, güç faktörünün düzeltilmesi ve verimin en büyük halini alması işlemine kompanzasyon denir.
Uygulamada fabrikalar, elektrik makineleri, iş makineleri ve motorlar endüktif çalıştıklarından bağlandıkları şebekeye reaktif güç verirler. Verilen reaktif güç aktif gücün dolayısıyla verimin oldukça düşmesine neden olur. İki eş sistemin kompanze edilmiş ve edilmemiş halleri karşılaştırıldığında çekilen akımın değişmediği, ancak aktif gücün arttığı görülür. İşte verimin artması ve şebekenin reaktif güçten kötü etkilenmemesi için endüktif sistemin girişine bir kompanzasyon kondansatörü bağlanır ve devrede üretilen reaktif güç şebekeye verilmeden kondansatörlerde depolanır. Motor devreye girerken de bu kondansatörler depoladıkları reaktif gücü motorlara geri verirler. Dolayısıyla şebeke sistemi saf resistif bir sisteme yakın olarak görür ve şebekeyle sistem arasında reaktif güç alışverişi olmaz.
Havai hatlarda kapasite[değiştir | kaynağı değiştir]

Havai nakil kablolarının her biri farklı bir fazı taşır, her bir kablonun sahip olduğu gerilim değeri anlık olarak değişmektedir ve kablolar arasında gerilim farkları oluşur. Kablolar kondansatör plakaları, aralarındaki mesafe yalıtkan kalınlığı ve aradaki yalıtkan da hava olarak hayal edilirse, havai nakil hatlarının oldukça büyük ve uzun bir kondansatör olduğu varsayalabilir. Her ne kadar kablolar arası mesafenin çok açık olması kapasite değerinde düşmeye yol açsa da bu kabloların kilometrelerce ilerlerdiği düşünüldüğünde, toplamdaki kapasite değeri hattın varış noktasında çıkış noktasına göre faz farkının oluşmasına neden olacaktır. Yani havai nakil hatlarının da bir kapasitesi vardır ve hesaba katılır.
Havai hatların kapasite değerleri kablonun cinsine, kablo aralığına göre değişir. Havai hatlar çekilirken kullanılacak kablonun kilometre başına kapasite (F/km) değeri kataloğundan okunur. Buna göre hesaplama yapılır.
Doğrultma[değiştir | kaynağı değiştir]


Kondansatörler içlerinde biriktirdikleri enerjiyi yüke boşaltmak suretiyle doğrultucu devrelerinde de kullanılabilirler. En basit doğrultuculardan olan yarım dalga doğrultucuda yüke ulaşan gerilimin grafiği alttaki resimde görülür. Ancak DC gerilimle çalışan bir alet için elde edilen bu gerilim grafiği uygun değildir. Çünkü aletin istediği, bir pilden elde edilebilecek kadar düz ve pürüzsüz bir gerilimdir.
Yandaki şemada yarım dalga doğrultucuya bağlı bir yüke paralel kondansatör bağlanması örneği görülür. Gerilim artarken yük depolayan kondansatör, gerilimin düşmeye başlayınca, yani ifadesinde bulunan gerilimin türevi negatif değer alınca içindeki elektrik yükünü, yüke iletmeye başlar. Bu noktadan itibaren AC gerilim azalırken, kondansatör bir kaynak gibi davranır ve içindeki yükü önündeki empedans değerine göre boşaltır. Yüke iletilen gerilimin grafiği yandaki resimde üstteki gerilim grafiği haline gelir. İlk duruma göre bu grafik DC gerilime daha yakındır. Bu da DC gerilimle çalışan bir aletin düzgün şekilde çalışması için daha uygundur.
Kararlılığa ulaşmış bir kondansatörlü doğrultma devresi göz önüne alındığında, üstteki grafikte gerilimin bir maksimum ve bir minimum değerleri olduğunu görürüz. Bu iki değer arasındaki fark dalgacık (ripple) olarak adlandırılır. Bu dalgacıkların genliği ne kadar düşük olursa o kadar doğru gerilim değerini yakalanmış olur.
Doğrultucuda kullanılan kondansatörlerin kapasite değerleri de elde edilen gerilim grafiğini etkiler. Kapasiteleri farklı 3 kondansatör aynı doğrultucu devresine bağlandığında grafikte olduğu gibi kapasite değeri arttıkça yük geriliminin DC gerilime yaklaştığı görülür. Bunun nedeni ise kondansatörün kapasitesinin arttıkça depoladığı yük miktarının artması ve bu elektrik yükünün daha uzun süre yükü beslemesidir. Yani kısaca, doğrultucu kondansatörlerinin kapasite değerleri arttıkça, DC gerilime yaklaşım sağlanır ve dalgacık genliği düşer.
RC filtreleme ve matematiksel işlemler[değiştir | kaynağı değiştir]
RC filtreler bir direnç ve bir kondansatörün bağlanmasıyla oluşturulur. Bu filtrelerin görevleri adlarında belirtilir. Görevleri belli frekansların geçmesini belli frekansların ise söndürülmesini sağlamaktır. Aynı şekilde bu devrelerin matematiksel analizi yapıldığında bir matematiksel operatörün ifadesi elde edilir. Yani RC devreleri frekans geçirme görevlerinin yanında matematiksel işlev operatör elde edilmesi için de kullanılan devrelerdir.

Alçak geçiren (AG) filtre - İntegral alıcı[değiştir | kaynağı değiştir]
Bu RC devresinin görevi isminden de belli olduğu üzere alçak frekansları geçirmektir. Yandaki devre şemasında da görüldüğü gibi bir direnç ile bir kondansatör birbirine seri halde bağlanıp, AC kaynak altında kondansatörün uçları arasındaki gerilim değeri okunur ve toplam gerilim ile çıkış gerilimi arasında frekans analizi yapılırsa bu sistemin belli bir frekans değerinden düşük frekansları aynen geçireceği, bu frekans değerinin üzerindeki frekansları ise hızlı bir şekilde söndüreceği görülür.
Ayrıca aynı sistemin gerilim analizi zaman domenine göre yapıldığında görülecektir ki kondansatörün uçları arasındaki gerilim, giriş geriliminin integrali alınmış ve bir sabitle çarpılmış haline eşittir. Dolayısıyla bu devre aynı zamanda integral alıcı devre olarak da anılır. İntegral ifadesinin önündeki sabit de bağlanan elemanların direnç ve kapasite değerlerine bağlıdır.

Yüksek geçiren (YG) filtre - Türev alıcı[değiştir | kaynağı değiştir]
Yine aynı şekilde bu RC filtresinin görevi de isminden bellidir. Yanda şeması gösterilen devreden de anlaşıldığı gibi bir direnç ve bir kondansatör seri bağlanır ancak bu sefer direncin uçları arasındaki gerilim değeri okunur. Ardından yapılan frekans analizinde görülür ki bu devre bir frekans değerinden düşükte kalan frekansları geçirmeyip söndürmekte, o frekans değerinden yüksek frekansları ise aynen geçirmektedir.
Gerilim analizi zaman domeninde yapıldığı zaman ise direncin uçları arasındaki gerilimin giriş gerilimin türevi alınmış ve bir sabitle çarpılmış haline eşit olduğu görülür. Bu sabit yine direnç ve kapasite değerlerine bağlıdır. Bu sebeple bu devreye türev alıcı devre adı da verilebilir.
Tasarım[değiştir | kaynağı değiştir]
Yalıtkan malzeme[değiştir | kaynağı değiştir]
Dielektrik (yalıtkanlık) sabiti[değiştir | kaynağı değiştir]
Yalıtkan bir malzemenin içinde depolayabileceği yük miktarı o malzemenin bir karakteristiğidir, yani farklı malzemelerin aynı koşullarda depolayabilecekleri yük miktarı da farklı olur. Bir malzemenin üzerinde yük depolayabilme yeteneği yalıtkanlık (dielektrik) sabiti adı verilen katsayı ile ölçülür ve bu katsayı her malzemede farklı değer alır. Hesaplama kolaylığı açısından her malzemenin dielektrik katsayısı, boşluğun dielektrik katsayısına göre oranlanır ve ortaya çıkan yeni katsayıya bağıl dielektrik (yalıtkanlık) sabiti adı verilir, kısaca vakumun yalıtkanlığı temel alınarak diğer malzemelerin yalıtkanlığı buna göre kıyaslanır. [18] Bir yalıtkan malzeme bağıl dielektrik sabiti oranında, vakuma göre daha fazla yük depolar. Alttaki kutuda vakumun dielektrik sabiti verilmiştir.
Hakkında Bilgi
| Vakumun dielektrik sabiti Malzemeye özgü bağıl dielektrik sabiti |
Delinme gerilimi[değiştir | kaynağı değiştir]
Yalıtkan malzemelerin karakteristikleri arasında gerilime dayanıklılık da sayılmalıdır. Bir malzemenin yalıtkanlığını yitirip deforme olduğu gerilim değerine bozulma - delinme gerilimi adı verilir ve yalıtkanlar için önemli bir göstergedir. Kondansatörlere delinme gerilimlerinden büyük bir gerilim kesinlikle uygulanmamalıdır, çünkü bu şekilde kondansatör iletken haline gelir ve işlevsiz kalır.[18]
Bazı yalıtkanların bağıl dielektrik sabitleri ve delinme gerilimleri
| Yalıtkanın İsmi |
Bağıl Dielektrik Sabiti | Delinme Gerilimi |
|---|---|---|
| Hava | 1 | 30,000 V/cm |
| Teflon | 2.1 | 600,000 V/cm |
| Polistren | 2.4 - 2.7 | 240,000 V/cm |
| Kağıt | 3.5 | 160,000 V/cm |
| Pireks (Cam) | 4.7 (3.7 - 10) | 140,000 V/cm |
| Silikon | 11.68 | 150,000 V/cm |
| Bakalit | 3.7 | 240,000 V/cm |
| Kuvartz | 3.7 - 4.5 | 80,000 V/cm |
| Mika | 4 - 8 | 800,000 V/cm |
Fiziksel yapı[değiştir | kaynağı değiştir]

Çeşitli fiziksel yapılarda kondansatörler temin edilebilir. Elektronik ve metalürji bilimlerinin gelişmesi, oldukça küçük ve farklı yapılarda kondansatör üretimini mümkün kılmıştır. Örneğin entegre devrelerin üzerinde mercimek ve pil şeklinde görülebilirler. Farklı yapıdaki kondansatörlerin kapasite değerleri belli başlı formülasyonlara göre hesap edilir. İki düz metal tabakadan üretilen kondansatör ile silindir veya daire şeklinde olan kondansatörün kapasiteleri farklı şekilde hesap edilir. Her ne kadar düzlemsel kondansatörün hesabı kolay olsa da 3 boyutluluk, silindiriklik ve küresellik devreye girdiğinde formulasyonlar oldukça karışık hale gelir.
Düzlemsel kondansatörler[değiştir | kaynağı değiştir]
Uygulamada oldukça fazla karşılaşılan bir kondansatör tipidir. Düzlemsel iki metal tabaka arasında belli bir dielektrik katsayısına sahip olan bir yalıtkanın yerleştirilmesiyle elde edilir.
Düzlemsel koordinatlarda gerilim değişimi bir boyutta gerçekleşir. Değişimin sadece x ekseninde olduğu yandaki şekilden görülür. İki kalın çizgi metal tabakaları belirtirken, aradaki kadar uzaklık içerisine yalıtkan bir malzeme yerleştirilir. Metal tabakaların alanları olup, birinin gerilimi iken diğer tabakaya gerilimi uygulandığında elektrik alanı , yüksek gerilimden düşük gerilime doğru olur.
Tabaka üzerinde herhangi bir noktada gerilim yani ve ekseni üzerinde gerilim değişmez. Yalıtkan malzeme gerilime karşı bir direnç gösterir ve bu sebeple gerilim düşümü ekseni üzerinde olur, bir tabakadan diğerine geçerken gerilim değerinden değerine düşer. Kondansatörün gerilim uygulanmayan plakasının , gerilim uygulanan plakasının konumlarında bulunduğu göz önüne alınır ve hesaplamalar sonucunda düzlemsel kondansatörün kapasite değerinin nelere bağlı olduğu bulunur.
Bu ifadeye göre düzlemsel kondansatörlerde kapasiteyi değiştiren etmenler, aradaki malzemenin dielektrik katsayısı, malzemenin kalınlığı ve metal plakaların yüzey alanıdır. Yüzey alanı, dielektrik katsayısı arttıkça ve aradaki mesafe azaldıkça kapasite artar.
Küresel kondansatörler[değiştir | kaynağı değiştir]

İç yarıçap = r1
Dış yarıçap = r2
Küresel kondansatörler iki metal kürenin iç içe konulup aralarına bir yalıtkanın yerleştirilmesiyle oluşturulur. Gündelik hayatta fazla kullanım alanı yoktur, genellikle yüksek gerilim tekniğinde benzetim yapmak için kullanılır ve kolaylık sağlar. Farklı çeşitleri mevcuttur, kürelerin merkezleri birbirindek ayrık, küreler birbiriyle ilişkisiz olabilir. Ancak hesaplamada kolaylık olması açısından eşmerkezli küresel kondansatörler kullanılacaktır.
İç küre yarıçapının , dış küre yarıçapının olduğu kabul edilir. Kondansatör ekseninde ise yine ve uzaklıkları arasında yer alır. İç küreye gerilim uygulanıp, dış küreye gerilim uygulanmadığında, sistem belli bir değerde yük depolama özelliğine sahip olur. Eşmerkezli küresel kondansatörlerde kapasite değerinin ifadesi aşağıdaki gibi yazılabilir.
Bu ifadede kesin olan tek şey, aradaki malzemenin dielektrik katsayısının kapasite değerini doğru orantılı etkilediğidir. ve yarıçapları ise alacakları değerlere göre kapasite değerini etkilerler, bu oran tasarım açısından çeşitlilik olanağı sunar.
Silindirsel kondansatörler[değiştir | kaynağı değiştir]

İç yarıçap = r1
Dış yarıçap = r2
Silindir uzunluğu = l
Silindirsel kondansatörler iki metal silindir tabakanın birbirinin içine yerleştirilmesi ve aralarına yalıtkan bir malzemenin koyulmasıyla tasarlanır. Bu tip kondansatörlerin günlük hayatta kullanımı çoktur. Kablolar, yüksek gerilim havai hatları veya geçit izolatörleri bu kullanım alanlarına örnek olarak verilebilir.[19] Benzetim açısından da kolaylık sağlayan silindirsel kondansatörlerin incelenmesinde eşeksenli olanları kullanılır.
İç silindir yarıçapı , dış silindir yarıçapı iken, silindir uzunlukları olarak alınır. Gerilim iç silindire uygulanır, dış silindir ise gerilimsiz bırakılır. Bu durumda sistem yalıtkan malzeme üzerinde yük depolar. Kapasite değeri ise aşağıdaki gibi bulunur.
Eşeksenli silindirsel kondansatörlerde kapasite değeri, yalıtkan malzemenin dielektrik sabitinden ve silindir uzunluğundan doğru orantılı olarak etkilenir, bu ikisinin artması kapasiteyi artırmaktadır. Doğal logaritmik ifadenin içerisinde gelen yarıçaplar oranı ise ters orantılı bir etki yapar. Yarıçaplar arasındaki oranda oynama yapılarak çeşitli değerlerde silindirsel kondanstörler elde edilebilir.
İmalat[değiştir | kaynağı değiştir]
Kondansatörlerde elektrotların birbirlerine göre konumları düzlemsel, küresel ve silindirsel olmaları hakkında bilgi verir, farklı fiziksel yapılar farklı ihtiyaçlar için geliştirilmiştir ve seçenekleri artırıp uygulama çeşitliliğine uyum sağlarlar. Kondansatör imalatında asıl önemli olan, kullanıcıların isteklerini karşılayacak şekilde, farklı uygulamalar için farklı ürünler imal etmek, bunları imal ederken de kapasite değeri ve çalışma gerilimi üzerinde ayarlamasında farklı yalıtkan malzemelerin farklı yalıtkanlık özelliklerinden faydalanılır.
Kapasite değeri, yalıtkan malzemenin incelmesi (elektrotların birbirine yaklaşması) ve elektrot alanının artmasıyla artar fakat yalıtkanların incelmesi malzeme açısından üretimde zorluk yarattığı gibi çalışma geriliminin azalmasına yol açtığından çok da avantajlı değildir. Ayrıca elektrot alanının artması da kondansatör büyüklüğünün artmasına neden olacağından bir yerden sonra kullanışsızlığı peşinden getirmektedir. Dolayısıyla imalat ve tasarım aşamasında bir optimizasyona gidilmelidir. İstenen kapasite ve çalışma değerlerinin en küçük ve kullanışlı boyuta nasıl getirilebileceği tasarlanmalıdır. Bu tasarlama çalışmaları farklı yalıtkanların kullanıldığı farklı kondansatörlerde yalıtkanların özellikleri göz önüne alınarak yapılır.
Kondansatörlerde alüminyum, gümüş veya kurşun elektrotlar kullanılır ancak alüminyum elektrot kullanımı en yaygın olanıdır. Yalıtkan farklılıkları ise kondansatörler arasındaki temel farkı oluşturur. Yalıtkan ile alüminyum film iletkenlerinin oluşturduğu kondansatöler ise bir kabın içerisine yerleştirilir ve enerjili kısım yalıtılmış olur.
Sargı yöntemi[değiştir | kaynağı değiştir]

Kondansatörlerde küçük boyutta istenen kapasite değerini elde etmenin yollarından biri elektrot alanında artırım yapmaktır, ancak elektrotlar düzlemsel olarak kullanıldığında alan arttıkça kondansatör boyutu de artmaktadır. Kondansatörlerde sargı yöntemi, elektrot alanında artma elde ederken boyutlardaki artmanın daha kabul edilebilir seviyede kalması için uygulanan bir yöntemdir.
Sargı yöntemi düzlemsel kondansatörlerin küçük boyuta sığdırılması amacını taşıyan bir yöntemdir. Uygulanması için (yandaki resimden takip edilebilir) boy olarak makul ancak en olarak uzun elektrot ve yalıtkan malzeme seçilir. Elektrot ve yalıtkan malzemelerin kolayca bükülebilir olması sargı yöntemi için şarttır. Dıştan içe doğru sırayla yalıtkan - elektrot - yalıtkan - elektrot dizilimi sağlanacak şekilde malzemeler üst üste yerleştirilir. Ardından bir rulonun etrafına, oluşturulan bu kondansatör sarılmaya başlanır. Tamamen sargı haline gelmiş kondansatör yalıtkan bir kabın içerisine yerleştirilerek dış ortamdan yalıtılır. Görünüş olarak silindirsel kondansatöre benzese de temelde tasarlanan düzlemsel bir kondansatörün sarılmış halidir. Yandaki resimde görülen kondansatör, içteki alüminyum elektrot yani anota artı (pozitif) kutup bağlandığında çalışmaya başlayacaktır.
Kondansatörün kullanım alanına göre terminallerinin yani uçlarının yerleri tasarlanmalıdır. Radyal bir kondansatörde uçlar aynı kenardan aynı yöne doğru çıkarlar. Aksiyal kondansatörlerde ise bir uç tavandayken diğer uç taban kısmında olur ve ters yönlere doğru çıkarlar. Sargı işlemi gerçekleştirilmeden önce düzlemsel elektrotların aynı yöne bakan kenarlardan uzatılan uçlar radyal kondansatör, ters yöne bakan kenarlardan çıkarılan uçlar ise aksiyal kondansatör elde edilmesini sağlar.
Sargı yöntemiyle, düzlemsel kondansatör halinde bırakılsa kullanışsız olacak derecede büyük boyutlara ulaşabilecek kondansatör, çok küçük bir boyutta aynı işlevi görmüş olur. Kağıtlı (yağ emdirilmiş), alüminyum film gibi çeşitli kondansatörler bu şekilde elde edilirler.
Çok katlı elektrot yöntemi[değiştir | kaynağı değiştir]

Kondansatörlerde kullanılan yalıtkan malzemenin bükülmez olması durumunda sargı yöntemi gerçekleştirilemez. Elektrot alanının artırılması birçok elektrotun birbiri içine geçirilip, elektrotlar arasına esnek olmayan yalıtkan malzemeden yerleştirilmesiyle çok katlı elektrot yöntemi uygulanmış olur.
Birçok elektrot - yandaki resimden de takip edilebildiği gibi - ardışık olarak (bir tarak gibi) birbirlerinin içine geçirildiğinde, toplam elektrot sayısının bir eksiği kadar kondansatör paralel bağlanmış olarak elde edilir. Kondansatörün iki elektrot arasındaki mesafesi , malzemenin yalıtkanlık katsayısı , elektrotların birbirine bakan alanları ve toplam elektrot sayısı olduğu düşünülürse çok katlı elektrota sahip bir kondansatörün kapasite değeri aşağıdaki gibi bulunur.
Mika ve seramik, esnek olmayan ancak elektriği iyi yalıtan ve kolayca inceltilebilir malzemeler olduklarından, seramik ve eski tip mikalı kondansatörler bu yöntemle imal edilirler.
Kazalar, tehlike ve güvenlik[değiştir | kaynağı değiştir]
Kondansatörler enerji depolayan elemanlardır ve içlerindeki elektriksel yükü uzunca bir süre saklayabilirler. Güç girişi kesilmiş bir devrede bulunan kondansatör bile depo ettiği yükü boşaltarak devrenin diğer elemanlarının zarar görmesine yol açabilir. Devreden ayrılmasına rağmen uçları arasına herhangi bir yük bağlanmayan kondansatör depoladığı yükü uçları kısa devre edildiği an hızla boşaltır ve bazen öldürücü olabilen şoklara, elektrik yanıklarına neden olabilir. Örneğin görünüşte zararsız olan ve 1.5 Volt ile çalışan fotoğraf flaşları içlerinde 300 Volt'a kadar yük depolayabilen kondansatörlere sahiptirler, bu kondansatörlerde depolanan enerji bir insanı kolayca çarpabilir ve şoklara yol açabilir.
Yüksek kapasite değerine sahip veya yüksek gerilimde çalışan kondansatörlerle çalışılırken dikkatle davranılır, kondansatörün tamamen boşaldığından emin olduktan sonra temas etmek sağlık açısından faydalıdır. Kondansatörler devreden söküldükleri anda yük depolamış halde bulunurlar, bu sebeple içlerindeki elektriksel yükünü boşaltmak için sönümlendirici direnç adı verilen, değeri akımı zararsız hale getirecek kadar yüksek ancak çok uzun olmayan bir sürede kondansatörü boşaltacak kadar da düşük olan bir direnç, kondansatörün uçları arasına temas ettirilir ve tam boşalmanın sağlandığından emin oluncaya kadar beklenir. Yüksek gerilim kondansatörleri istiflenirken uçları arasına bir yalıtkanla kesinlikle kısa devre yapılır, çünkü bu tip kondansatörler cidden büyük zararlara yol açabilecek yükleri içlerinde depolayabilirler.
Eski yağ emdirilmiş büyük kondansatörler poliklorlanmış bifenil (PCB) içerirler. PCB bileşikleri artıkları topraktan yeraltı sularına karışabilmektedir. PCB'ler içme suyuyla çok az bir miktarda tüketilse bile kanserojen etki göstermektedir. PCBlerin insan vücuduna karışması aşağıdki yollarla olabilmektedir;
- Yiyecek veya içeceğe karışması,
- deri yoluyla emilmesi,
- buharının solunması yoluyla. (Oda sıcaklığındaki PCB buharı herhangi bir sağlık riski yaratmaz.)
Bu nedenlerden dolayı eski büyük tip yağ emdirilmiş kondansatörler için çeşitli önlemler alınmalı, akıntı yapmış kondansatörler kesinlikle güvenli bir şekilde yok edilmelidirler. Bu sağlık risklerinden dolayı artık PCB içeren kondansatörler üretilmemekte ve kullanımda olanlar tedavülden kaldırılmaktadır.
Kondansatör sanayisi[değiştir | kaynağı değiştir]
Genel bakış[değiştir | kaynağı değiştir]
İnsanlığın iki metal tabaka arasına bir yalıtkan malzeme yerleştirmek suretiyle icat ettiği kondansatörler, büyük bir sanayi alanı oluşturmuş ve günümüzde milyonlarca doların döndüğü bir pazar haline gelmiştir. Öyle ki farklı uygulamalar için farklı büyük alt kollara ayrılmış, pazar içinde birçok pazar oluşturmuştur. Kondansatör sanayisi, diğer teknolojik gelişmelerden fazla etkilenmemiş, yapımında kullanılan malzemelerin çeşitliliğinden ziyade yapı ve fiziksel boyutunda gelişmeler görülmüştür.

Alüminyum hâlâ elektrotlarda kullanılan yegane malzemedir. Yağ emdirilmiş kâğıtların yalıtkan malzeme olmaktan çıkması ise 1960'lı yıllara rastlar. Plastik filmlerin yalıtkan olarak kullanılmasıyla beraber kondansatör teknolojisinde en büyük ilerleme kaydedilmiş, kâğıtlı kondansatörler tedavülden kalkmaya başlamış ve kuru yalıtkanlı kondansatörler ortaya çıkmıştır. Yine bu ilerlemeyle birlikte kondansatör imalatında devrim niteliğinde gelişmeler olmuş, çok küçük boyutlu ve ucuz kondansatörlerin üretimi mümkün olmuştur.
Modern kondansatör sanayisindeki büyüme, II. Dünya Savaşı'nda elektronik bilimindeki gelişmelerle tetiklenmiştir. Barışın sağlanmasının ve elektronik bilimine yeni alt dalların eklenmesinin ardından dünya genelinde kondansatör ihtiyacı inanılmaz bir şekilde artış göstermiştir. Ancak yandaki grafikte de görüldüğü gibi, üreticiler açısından şanssız bir durum olarak, kondansatör sanayisi dünya ticaretindeki ihtiyaç artış ve azalmalarından oldukça fazla etkilenmiştir, bu da tüketicilerin kondansatör ihtiyacında büyük değişikliklere yol açmıştır. Bu sebeple de kondansatör üreticileri öngörü yapmakta zorlanmış ve ağzı sıkılığı tercih etmiştir.
Farklı kollardaki gelişmeler[değiştir | kaynağı değiştir]
- Plastik film kondansatörler: Yalıtkan malzeme olarak kâğıdın yerini plastik türevlerinin almasıyla birlikte kondansatör sanayisinde büyük bir gelişme gözlenmiştir. Öncülüğü polyesterin yapmasıyla birlikte polikarbonat, polistren ve poliprolen gibi malzemeler, farklı yalıtkanlık özelliklerinden faydalanılarak kullanılmışlardır. Özellikle geçmişte AC akımda kullanılan ve yalıtkan olarak P.C. B (poliklorlu bileşikler) taşıyan kondansatörlerin çevre kirliliğine neden olduğunun belirlenmesinin ardından, poliprolen yalıtkanlı kondansatörler AC devrelerde yaygınlaşmaya başlamıştır. Yağ emdirilmemiş kuru yalıtkanlı kondansatörlerin AC motorlarında ve floresan lambalarda kullanımının yaygınlaşmasının ardından kısa süre içerisinde hem çevreye zararsız hem de devreler için uygun büyüklüklerde kondansatörler imal edilmesi olanaklı hale gelmişti. DC akım için kullanılan kondansatörlerde de durum hemen hemen aynıydı ancak kâğıtlı kondansatörler bir süre daha yaşamaya devam ettiler. Sadece modası geçmiş devrelerde kullanım alanı bulabiliyorlardı ancak bu alan da zamanla plastik film kondansatörleri tarafından ele geçirildi. Bu gelişmelerin ardından kâğıtlı kondansatörler piyasadan silindi, yerlerini plastik filmli kondansatörler aldı ve 1980 yılında plastik film yalıtkanlı kondansatörler piyasanın % 20'lik bir kısmını kapsamaktaydılar.
- Seramik kondansatörler: Kondansatör sanayisinin gelişiminde plastik film gibi seramik yalıtkanlı kondansatörlerin de büyük etkisi vardır. Transistor gibi elektronik elemanların yaygınlaşmasıyla birlikte düşük gerilim değerlerinde çalışabilen kondansatörlere ihtiyaç duyuldu. Toleranlarının kararlı olmaması ve sınırlı yüksek gerilimde çalışabilmeleri dezavantajlarına rağmen düşük gerilimde çalışan devreler için disk seramik kondansatörler oldukça makuldü. Baskı devre üretiminin artmasıyla birlikte Amerika, Japonya ve Avrupa'da üreticiler haftada ortalama 1 milyon disk seramik kondansatör imal etmeye başladılar.
- Elektrolitik kondansatörler: Vakum tüplerinin tedavülden kalkıp yerine daha kararlı elektronik elemanlarının gelmesiyle birlikte elektrolitik kondansatör ihtiyacında büyük bir artış görüldü. Tüketici taleplerinde meydana gelen değişimler, üreticilerin kondansatörler için kapasite ve gerilim taleplerinde değişmeye yol açmıştır. Çünkü artık küçük devreler için yüksek kalitede ve uzun ömürlü kondansatörler gerekiyordu, bu gelişmeler sonucunda elektrolitik kondansatör piyasası gelişti. 1980'li yıllarda bu tip kondansatörler piyasanın % 37'sini elinde tutmaktaydı.
Günümüzde kondansatör sanayisi[değiştir | kaynağı değiştir]
Kondansatör pazarında 2000 yılında rekor kırılmasının ardından 2001 - 2002 yıllarında piyasa düşüşe geçmişti ve piyasanın yeniden hayat belirtisi göstermesi için 2003 yılının ikinci yarısına kadar beklenmesi gerekiyordu. Bu canlanış 2004'ün ilk yarısında gelen yüksek talep ve sabit fiyat sayesinde ivme kazandı. Ancak bazı ekonomik sebepler yüzünden 2005 yılında başlayan düşüş 2006 yılına kadar devam etti. Günümüzdeki ekonomi çevrelerindeki beklentiler kondansatör piyasasının 2009 yılına kadar büyük bir büyüme içerisine gireceği yönündedir.
2000 yılının sonunda haberleşme ve telekom teknolojileri piyasasında meydana gelen çöküşün ardından kondansatör sanayisi yeni bir yapılanmanın içine girdi ve farklı alanlarda mücadele etmek zorunda kaldı. Günümüzde kondansatör piyasası fiyatlandırma, malzeme fiyatlandırması ve ulaşılabilirlik, kondansatör teknolojileri arasındaki yarış, kapasite değerleri, Çin ve Tayvan gibi ucuz üretim yapan ülkeler hakkında acil önlemler, üretimin yıllar geçtikçe bu ülkelere kayması, kondansatörlerden kurşun gibi zararlı malzemelerin temizlenmesi ve daha zararsız malzemelerin kullanılması gibi alanlarda mücadele vermektedir.
Pasif elektronik elemanlar piyasasında Avrupa'da birinci, dünya genelinde ikinci büyük firma olan EPCOS'un kondansatör piyasası ile ilgili verileri kullanılarak piyasanın bugünü ve geleceği daha iyi takip edilebilir. Merkezi Almanya'da bulunan firma kondansatörler, seramik elemanlar (seramik kondansatörler dahil), ferrit ve endüktanslar gibi alanlarda söz sahibidir. EPCOS kondansatör fabrikası alüminyum, tantalum, film, güç kondansatörü ve ultrakondansatör üretimi yapmaktadır.
Firmanın kondansatör satışlarında 2004 yılında bir önceki yılın aynı dönemine göre % 1.1 artış gözlenmiştir ve satış 350 milyon €'dan 354 milyon €'ya çıkmıştır. Yılın son çeyreğinde ise yine geçen yılın son çeyreğine göre % 7'lik bir satış artışı görülmüş ve satış 83 milyon € olmuştur. Bu artışı otomotiv ve endüstriyel elektronik alanında ortaya çıkan alüminyum kondansatör ihtiyacı sağlamıştır. Tüketicilerin film kondansatör ihtiyacındaki artış yine satışı artırmıştır ancak tantalum kondansatörlerin bu artışta payı yok denebilecek düzeydedir.
Aşağıdaki iki liste EPCOS firmasının 2003 yılında yaptığı kondansatör satışlarının hangi endüstriye yüzde olarak ne kadar yapıldığını ve kondansatör çeşitlerinin toplam satış içerisindeki payını göstermektedir.
| Endüstrisine göre kondansatör satışları |
Çeşitlerine göre kondansatör satışları | ||
| Teknolojik ürünler | % 38 | Tantalum | % 33 |
| Otomotiv | % 21 | Alüminyum | % 29 |
| Telekomünikasyon | % 14 | Film | % 21 |
| Tüketici – Perakende | % 8 | Güç kondansatörü | % 16 |
| Diğer dallar | % 19 | Ultrakondansatör | % 1 |
| Toplam | % 100 | Toplam | % 100 |
Kaynakça[değiştir | kaynağı değiştir]
- James W. Nilsson - Susan A. Riedel (1996). Electric Circuits - 7th Edition ISBN 0-13-127760-X
- Haluk Erna (1977). Pratik Elektrik ve Uygulamalarla Modern Elektroteknik ISBN 975-10-1419-0
- Tanju Batıbeki (1992). Elektronik Öğreniyorum
- The Electronics Club 19 Ağustos 2007 tarihinde Wayback Machine sitesinde arşivlendi.
- How Stuff Works14 Kasım 2004 tarihinde Wayback Machine sitesinde arşivlendi.
- VIAS Ancyclopedia 14 Temmuz 2008 tarihinde Wayback Machine sitesinde arşivlendi. Dielectric Constant Maddesi
- Peter D. Driver, The Development of the Capacitor Industry and its Position in World Markets, ElectroComponent Science and Technology, 1978.
- ^ a b "TDK Güncel Türkçe Sözlük". 29 Aralık 2018 tarihinde kaynağından arşivlendi.
- ^ a b c Colin A. Ronan (1983). Bilim Tarihi: Dünya Kültürlerinde Bilimin Tarihi ve Gelişmesi, Ekmeleddin İhsanoğlu, Feza Günergun (Çev.) (2003). ISBN 975-403-275-0 (s. 424 - 425)
- ^ The story of electrical and magnetic measurements: from 500 B.C. to the 1940s
- ^ a b Ramasamy Natarajan, Power System Capacitors. p.p 1 - 3
- ^ a b c Elektrik Mühendisleri Odası eğitim dokümanı 14 Mart 2013 tarihinde Wayback Machine sitesinde arşivlendi., erişim tarihi: 27 Ağustos 2011
- ^ Kondansatörlerin üzerindeki değerler neyi ifade eder?, İstanbul Üniversitesi web sitesi. Erişim tarihi: 28 Ağustos 2011
- ^ Yıldız Teknik Üniversitesi, Mesleki Terminoloji 13 Ağustos 2011 tarihinde Wayback Machine sitesinde arşivlendi., s.74. Erişim tarihi: 27 Ağustos 2011
- ^ Watson, Linda, Illustrated dictionary of electrical engineering, Lotus Press, 2005, s.194
- ^ "For some materials, variation of capacitance with temperature is approximately linear." Glisson, Tildon H., Introduction to Circuit Analysis and Design, Springer, 2011, s. 258
- ^ "Ceramic materials are affected by voltage, temparature and frequency (...) Capacitance change with temparature is non-linear." Mazda, F.F., Discrete electronic components, CUP Archive, 1981, s. 78
- ^ "Ceramic dielectric capacitors very widely in both dielectric constant and temparature characteristics (...) The higher the k, the worse is its temperature characteristics" Bowick, Chris; Blyler, John; Ajluni, Cheryl (2007). RF circuit design, Newnes, s.6
- ^ a b c d Slone, G. Randy, TAB electronics guide to understanding electricity and electronics, McGraw-Hill, 2000, s.135
- ^ "Arşivlenmiş kopya". 23 Ağustos 2007 tarihinde kaynağından arşivlendi. Erişim tarihi: 29 Ağustos 2007.
- ^ James W. Nilsson - Susan A. Riedel (1996). Electric Circuits - 7th Edition, ISBN 0-13-127760-X (s. 452 - 453)
- ^ [1] 26 Ağustos 2007 tarihinde Wayback Machine sitesinde arşivlendi. HowStuffWorks İnternet Sitesi How Capacitors Work - Kondansatörler Nasıl Çalışır?
- ^ Richard Ulrich, 2004. Matching embedded capacitor dielectrics to applications, Circuit World, ISSN 0305-6120
- ^ [2] 13 Eylül 2007 tarihinde Wayback Machine sitesinde arşivlendi. HowStuffWorks İnternet Sitesi How Camera Flashes Work - Kamera Flaşları Nasıl Çalışır?
- ^ a b [3][ölü/kırık bağlantı] EMO - Teknik Bilgiler İnternet Sitesi
- ^ a b c d Özcan Kalenderli, Celal Kocatepe, Oktay Arıkan (2005). Çözümlü Problemlerle Yüksek Gerilim Tekniği - Cilt I, ISBN 975-511-420-3 (s. 33)
- ^ Peter D. Driver, 1978. Electrocomponent Science and Technology Vol. 5, p.120
Dış bağlantılar[değiştir | kaynağı değiştir]
| Wikimedia Commons'ta Kondansatör ile ilgili ortam dosyaları bulunmaktadır. |
- Kondansatörler (www.silisyum.net) 17 Ağustos 2007 tarihinde Wayback Machine sitesinde arşivlendi.
- Kondansatör nedir? (www.antrak.org.tr)
- Kondansatör nedir? (www.akmtele.com)
- Kondansatör nasıl çalışır? (howstuffworks.com)9 Şubat 2010 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce)
















![{\displaystyle \ i_{C}=C\cdot {\frac {dv_{C}}{dt}}\to [i={\mbox{Amper}},t={\mbox{saniye}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0487546d31f0507aa2b8eb42b59117f49309829a)








![{\displaystyle \ \phi _{v}=0\to v_{max}\cdot e^{j(-90^{\circ })}=v_{max}\cdot [\cos(-90)+j\sin(-90)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c35906861e3a2fbbcd93fad0cd468d5437221e36)

























![{\displaystyle \ p={\frac {v_{max}\cdot i_{max}}{2}}\cos(\phi )[1+\cos(2\omega t)]-{\frac {v_{max}\cdot i_{max}}{2}}\sin(\phi )\sin(2\omega t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/440531bac2d417ee5337e9018a09edc78fdc99ca)




![{\displaystyle \ p={\frac {v_{max}\cdot i_{max}}{2}}\cos(\phi )[1+\cos(2\omega t)]+{\frac {v_{max}\cdot i_{max}}{2}}\sin(\phi )\sin(2\omega t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9647741897c2c99f199d47f7779fa53e72468487)




![{\displaystyle \ p={\frac {v_{max}\cdot i_{max}}{2}}\cos(-90^{\circ })[1+\cos(2\omega t)]-{\frac {v_{max}\cdot i_{max}}{2}}\sin(-90^{\circ })\sin(2\omega t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f17f90a431d0233fc010ad308b12edc9513bdf6b)








































































