Klasik fizik

Modern Fiziğin dört ana alanı

Klasik fizik tamamlanmış veya uygulanabilir olan fiziğin, eski tarihlerde düşünülmüş modern teorilerle ilgilenir. Şu an kabul edilmiş bir teori modern sayılıyorsa ve o teorinin giriş cümlelerinde başlıca paradigma değişiminden bahsediliyorsa, eski teorilere (veya eski paradigmaya dayanan yeni teorilere) genellikle “klasik” denilir. Bir klasik teorinin tanımı aslında içeriğine bağlıdır. Klasik fizik kavramı, modern fizik için fazlasıyla karmaşık olan belirli durumlarda kullanılır.

Genel bakış

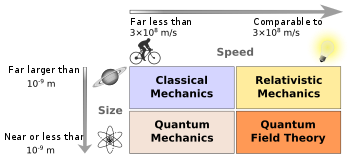
Klasik teorinin, fizik için çok farklı iki anlamı vardır. Kuantum mekaniği kavramında, klasik teori, niceleme paradigmasını kullanmayan, görelilik içeren klasik mekanik teorilerine bağlıdır. Buna genel kuantum mekaniğiyle iş birliği yapmayan, görelilik ve klasik elektromanyetizma gibi klasik alan teorileri dâhildir. Genel görelilik ve özel görelilik kavramında, klasik teoriler Galileo’nun görelilik kuramına itaat eder. Klasik fizikte yer alan teoriler ve dalları;

• Klasik mekanik
  • Newton'un hareket yasaları
  • Klasik Lagrange ve Hamilton mekaniği biçimciliği
• Klasik elektrodinamik (Maxwell denklemleri)
• Klasik termodinamik
• Özel görelilik ve Genel görelilik
• Klasik kaos kuramı ve doğrusal olmayan dinamik.

Modern fizikle karşılaştırılması

Klasik fiziğin tersine, “modern fizik”, kuantum fiziği ve 20-21. yüzyıl fiziğine genel olarak daha az bağlı bir kavramdır. Modern fizik, uygulanabilir olduğunda kuantum kuramı ve görelilik kuramı içerir.

Klasik fizik yasaları yaklaşık olarak geçerli sayıldığında bir klasik sistem, klasik limit kabul edilebilir. Pratikte, atom ve moleküllerden büyük fiziksel objeler klasik mekanik ile rahatlıkla anlaşılabilir. Buna iri ölçekli ve astronomik alandaki objelerde dâhildir. Klasik fizik yasaları atomsal düzeye inildiğinde, bozulur ve kesin sonuçlar vermez. Uzunluk ölçekleri ve alan kuvvetleri kuantum mekaniğinin etkilerinin geçersiz kabul edildiği büyüklüklerde elektromanyetik alanlar ve kuvvetler, klasik termodinamikle açıklanabilir. Determinist tabirler kuantum fiziğinde var olsa bile kuantum fiziğinin tersine klasik fizik tamamlanmış determinizm ilkeleriyle nitelenebilir.

Görelilik içermeyen klasik fiziğin bakış açısından, genel ve özel görelilik tahminleri, özellikle zamanın akışı, uzayın geometrisi, maddenim serbest düşteki hareketi ve ışığın yayılımı ile ilgilenen klasik fizik teorilerinin tahminlerinden çok daha farklıdır. Eskiden ışık yayılan ortamın sabit olduğu varsayılarak, daha sonraları var olmadığı ispatlanan esir denilen madde içinde ilerlelediği varsayılıyordu.

Matematiksel olarak klasik fizik denklemlerinde Planck sabiti görünmez. esir teoremi ve karşılılık ilkesine göre, süperakışkanlık gibi birkaç istisna dışında, bir sistem genişleyince veya ağırlaşınca klasik dinamik ortaya çıkar. İşte bu yüzden günlük hayatta kuantum mekaniğini ihmal ediyoruz. Fakat, klasik-kuantum uyumu günümüzde en hareketli alanlardan biridir. Bu alan, kuantum fiziği yasalarının klasik düzeyin sınırlarında klasik fiziğe nasıl yer verdiğiyle ilgilenir.

Bilgisayar modelleme ve elle hesaplama, modern ve klasik karşılaştırma

Yalnızca kuantum ve göreliliksel teoriyi kullanan bir bilgisayar modellemesi

Günümüzde bilgisayarlar, özel denklemin kaşifi Newton’un (diferansiyel calculus’ün babalarından biri) bile saatlerce uğraşıp çözebileceği klasik bir diferansiyel denklemi çözmek için saniyeler içinde milyonlarca aritmetik işlemler yapar.

Bilgisayar modelleme kuantum ve göreceli fiziği kullanır. Klasik fizik büyük sayıda parçacıklar için kuantum mekaniğinin sınırı gibi düşünülebilir. Öte yandan klasik mekanik (klasik fiziğin bir bölümü) göreliliksel mekanikten türetilir. Işık hızından çok küçük hızlar için c²’in paydada büyük olduğu terimler ihmal edilebilir. Daha sonra bu formüller Newton kinetik enerjisinin ve momentumunun standart tanımlarına indirgenir. Özel görelilik ve Newton mekaniği olması gerektiği gibi uyumlu. Bilgisayar modelleme mümkün olduğunca gerçekçi olmalıdır. Klasik fizik süperakışkanlık olayı gibi bir hata öne sürüyor. Kuantum teorilerinin zaman harcadığı doğrudur ve bilgisayar olanakları klasik denklemleri kullanmakla azalabilir. Ancak zamandan tasarruf etmek için güvenilirliği feda edemeyiz.

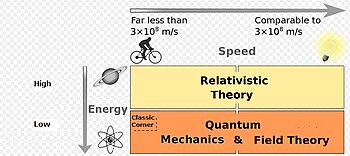
Bilgisayar modelleme bir nesneyi incelerken (herhangi sayıda parçacıklı bir parçacık sistemi) göreceli ya da kuantum, hangi teorinin kullanılmasına enerji kriterlerini kullanarak karar verir. Nesnenin hızı ve büyüklüğü (ya da parçacık sistemi) yalnızca akademik çalışmalarda ve mühendislik calculusünde kullanılır (inşaat mühendisleri bir köprü ya da ev yapmak için klasik fiziği kullanır). Bir fizikçi deneyin başlangıcında gerçek kalkulus işlemi başlamadan bir yaklaşımda bulunmak için klasik fiziği kullanır.

Bilgisayar modellemede klasik fizik hariç tutulursa nesnenin hızını kullanmaya ihtiyaç yoktur. Düşük enerjili nesneler kuantum teorisiyle, yüksek enerjili nesneler de görelilik teorisiyle halledilebilir. .