Açısal momentum
Açısal momentum, herhangi bir cismin dönüş hareketine devam etme isteğinin bir göstergesidir ve bu nicelik cismin kütlesine, şekline ve hızına bağlıdır. Açısal momentum bir vektör birimidir ve cismin belirli eksenler üzerinde sahip olduğu dönüş eylemsizliği ile dönüş hızını ifade eder.
Bir sistemin sahip olduğu açısal momentum, içerisindeki bireysel ufak parçacıkların sahip olduğu açısal momentumların toplamına eşittir. Simetri ekseni üzerinde dönüş yapan bir cismin açısal momentumu eylemsizliğinin (cismin yerinin değiştirilmesine ile açısal hızına ω müdahale edilmesine karşı yaratmış olduğu direnç) ürünü olarak hesaplanabilir. Formülü 'dir. Bu nedenle açısal momentum bazen "dönüş lineer momentumu" olarak ifade edilir.[kaynak belirtilmeli]

Kendi dönüş eksenine kıyasla çok daha ufak olan cisimlerde (örneğin çok uzun bir ip ucunda sallanan küçük lastik top veya Güneşin etrafında dönüş yapmakta olan gezegenler) açısal momentum, lineer dönüş momentumu olarak tanımlanabilir. Bu tanımda cismin kütlesi ve hızı dönüş ekseninin yarıçapı ile çarpılarak sonuç bulunur.
Sisteme dışarıdan herhangi bir tork uygulanmadığı sürece açısal momentum her zaman korunur. Örneğin buz pateni yapan biri kollarını içeriye doğru kapar ise kendisi hızlanır bunun sebebi açısal momentumun korunumudur. Nötron yıldızlarının çok fazla miktardaki dönüşleri de açısal momentumun korunuşu ile açıklanabilir. Açısal momentum korunumu çoğu fizik ve mühendislik bölümlerinde araç gereç üretiminde yararlanılmaktadır.
Klasik mekanikte açısal momentum[değiştir | kaynağı değiştir]
Bir merkeze göre alınan açısal momentum (L)un tanımı;
bu formülde r parçacığın merkeze göre yer vektörüdür, p parçacığın lineer momentumudur ve x vektör çarpımını ifade eder.

Tanımda da görüldüğü gibi açısal momentumun SI birimindeki değeri Newton metre saniyedir (N•m•s veya kg•m2/s) veya joule saniye (J•s). Vektör çarpımından dolayı açısal momentum, yarıçap vektörü r ve momentum vektörü p ye diktir ve bu sağ el kuralı ile bulunabilir. Sabit kütleli ve değişmeyen bir simetri ekseni etrafında dönüş yapan cismin açısal momentumu, eylemsizliğin ürünü olarak kabul edilir ve açısal hız vektörü; I cismin eylemsizliği (genellikle bir gergi birimi) ve ω açısal hızdır. Düz bir çizgi ekseninde dönüş yapan parçacık veya katı cismin açısal momentumu bir vektördür ve büyüklüğü ile yönü sabittir. Eğer dönüş ekseni cismin veya parçacığın merkezinden geçerse o noktada açısal momentum sıfırdır. Çünkü bahsi geçen noktanın dönüş hareketi mevcut değildir.
Bir parçacık topluluğunun açısal momentumu[değiştir | kaynağı değiştir]
Eğer bir sistem çok sayıda parçacık barındırıyorsa bu sistemin toplam açısal momentumu bu parçacıkların her birinin momentum toplamlarına eşittir. Sabit bir kütle dağılımının olduğunu ve cismin kütlesinin ρ = ρ(r), türevsel bir hız elemanı dV, yön vektörü r bize kütle elementi; dm = ρ(r)dV verir. Bu cismin bu sebeple sonsuz küçük açısal momentumu; dir. Bu formül üzerinde yapılan türev ve integral işlemleri sonucunda toplam açısal hız bulunur;
Kütle merkezi kullanılarak açısal momentum[değiştir | kaynağı değiştir]
Bir bütün halindeki parçacık gruplarının açısal momentumları bulunurken matematiksel işlemlerin kolaylığı açısından, kütle merkezi alınması genellikle uygun kabul edilir. Bir parçacık grubunun açısal momentumu her bir parçanın açısal momentumunun toplamına eşittir; ri i parçacığının yer vektörüdür, mi kütlesi, vi lineer hızıdır. Kütle merkezi şu formül ile ifade edilmiştir; tüm parçacıkların toplam kütleleri; Kütle merkezinin lineer hızı;
Ri i için kütle merkezine olan uzaklık, Vi i parçacığını lineer hızı ve sonuç olarak; ve
görüldüğü gibi; ve
Bu sebeple bir noktaya göre alınan açısal momentum;
Yazılan ilk terim kütle merkezinin açısal momentumudur. Bu sonuç tek bir M kütleli cisim için kütle merkezinde v hızı ile hareket etmiş olsa idi aynı açısal momentum olurdu. Yazılan ikinci terim ise her bir parçacığın kendi içerisindeki açısal momentumlarıdır. İkinci terim daha da basitleştirilebilir. Kütle merkezindeki parçacıkların eylemsizlikleri ve açısal hızları dönüş hareketinden dolayı toplanır ve açısal momentumu verir.
Sabit eksende dönüş[değiştir | kaynağı değiştir]
Eğer bir sistemde sadece dönüş ile ilgileniyorsak, cismin açısal momentumunu skaler bir birimmiş gibi inceleyebiliriz ve bunun için saat yönünün tersinde hareket ettiği zamanları incelemeliyiz. Bunu yapabilmek için formülümüzde vektör çarpımının yerine birim vektörü ekleriz ve açısal momentum böylelikle son halini alır; θr,p r ve p noktaları arasındaki hesaplanmış açıdır.

p’ye göre kaldıraç kol uzaklığıdır.
İşlem kolaylığı açısından düşünmemiz gereken kaldıraç kol uzaklığını merkeze ve p noktasından geçen bir çizgi üzerinde almamızdır. Bu tanımla beraber p noktasının yönünü (saat yönünü yoksa tersi mi) belirlenirse L nin işareti bulunabilir; p nin r üzerindeki dik bileşenidir. Görüldüğü gibi açısal momentumun işareti dönüş yönüne göre belirlenir.
Sabit kütleli ve sabit bir eksen üzerinde dönüş yapan cisimlerin açısal momentumu eylemsizliğin bir ürünü olarak kabul edilebilir ve açısal hız vektörü; I cismin anlık eylemsizliğidir ve ω açısal hızdır. Büyük kütleli bir cismin kinetik enerjisi T; formülü ile bulunabilir ve görüldüğü gibi açısal hızı karesi, kinetik enerji ile orantılıdır. Tıpkı ötelenimsel enerji ve ötelenimsel hız gibi. Genellikle açısal hız vektörü dönüş ekseni yönünde iken, açısal momentum bu yönde değildir. Bunun sebebi cisim üzerindeki kütle dağılımının nasıl olduğunu bilmememizdendir. Genellikle yönler ve büyüklükler arasındaki bağlantılar ω ve L yönleri eylemsizliğin ikinci dereceden gergisinden bulunur; gergi tanımlaması uygulanır ve toplam işlemleri yapılırsa (i, j = 1, 2, 3) Kinetik enerjinin genel tanımı;
Açısal momentumun korunumu[değiştir | kaynağı değiştir]
Açısal momentumun korunumu yasası, kapalı bir sistemdeki cisme dışarıdan herhangi bir tork etki etmediği sürece açısal momentumda bir değişiklik olmayacağını tanımlar. Herhangi bir olay öncesinde cisim üzerinde sadece iç torklar etki ettiği için açısal momentumda bir dış tork olmadığı sürece değişme görülmez. Bu korunum yasası matematiksel olarak yön bağımsızlıktan bulunur ve sonsuz yön kabul edildiği için hiçbir yön bir diğerinden ayrı değildir. Noether teoreminde de görüldüğü gibi açısal momentumun zamana göre türevi torktur;
Hız ve momentumun vektör çarpımı sıfırdır çünkü vektörler paraleldir. Sistemin kapalı olduğu kabul edilirse ve matematiksel olarak sıfır kabul edilirse dışarıdan etki edebilecek sıfır tork; sistemdeki parçacıklara etki eden torktur. Sistem içindeki kuvvetlerin Newton’unun üçüncü yasasına uyduğu kabul edilir. Bu demektirki parçacıkların birbirlerine uyguladığı kuvvetler birbirlerine eşittir. Yörüngelerde ise açısal momentum gezegenin hem kendi etrafında hem de yörüngesi etrafındaki dönüşüne dağılmıştır. ;
Eğer bir gezegenin beklenildiğinden daha yavaş hareket ettiği gözlemlenirse bunun sebebi gezegenin etrafında bir uydusu olmasıdır ve toplam açısal momentum gezegen ve uydusu arasında bölüşülür.
Açısal momentum genellikle kütleçekim kuvvetinin incelenmesinde kullanılmıştır. Eğer net kuvvet bir cismin sürekli olarak merkezine uygulanıyorsa bu cismin merkezine göre torku yoktur ve bu sebeple cismin açısal momentumu sabittir. Açısal momentumun sabit olması gezegenlerin yörüngelerini incelerken ve Bohr atom modelleri incelirken çok kullanışlıdır.
Açısal momentumun korunumunun en kolay açıklanabildiği olaylardan biri bir buz patencisinin hareketleridir. Kollarını dikey dönüş eksenine göre kapattığı zaman hızlanmaktadır. Kollarını kendine doğru çektiği zaman gövdesinin anlık eylemsizliğini düşürmektedir ve açısal momentum sabit olduğu için dışarıdan bir tork etki etmediği sürece açısal hız artacaktır.
Aynı olay çok hızlı dönmekte olan yıldızlar içinde geçerlidir (beyaz cüce, nötron yıldızları, kara delikler). Bu cisimler oluşurken kendilerinde daha büyük ve daha yavaş dönüş yapan yıldızlardan meydana gelmişlerdir (bir cismin boyutunun 104 azaltılması, açısal hızının 108 kat artmasına neden olur.
Dünya ve Ay arasındaki açısal momentumun korunumu aralarındaki açısal momentum transferleriyle gerçekleşir. Dünya ve Ay arasındaki bu geçişler dalga torklarında kaynaklanır. Bu olaylar dünyanın dönüş hızını yaklaşık 42 ns/gün [kaynak belirtilmeli] azaltır ve Ay’ın yörüngesinin ~4.5 cm/yıl oranında [kaynak belirtilmeli] artmasına neden olur.
Açısal momentum (modern tanım)[değiştir | kaynağı değiştir]
Modern (20.yüzyılda teoremsel fizik ve açısal momentum bir iç açısal momentum olarak kabul edilmemiştir) fizikte açısal momentum daha farklı bir yolla formülize edilmiştir.

Bu formülde açısal momentum, Noether birimlerini ikinci formu olarak kabul edilir. Sonuç olarak açısal momentum uzay zamanda genellikle korunmaz ta ki asimptotik olarak dönüşü değiştirilmez ise.
Klasik mekanikte bir parçacığın açısal momentumu bir düzlem elemanı olarak tanımlanabilir; bu formülde dış çarpım& ve vektör çarpımı x in yerini alır. Bu daha basit bir geometrik düzlem oluşturulmasını sağlar ve x ile p vektörleri kullanılır. İşlemler iki veya daha fazla boyutlar için geçerlidir. Kartezyen koordinatlarda; veya daha detaylı iç gösterim ile; Bu açısal hız tanımı anti simetrik ikinci dereceden gergi olarak da tanımlanabilir birimleri; ωij. Bu iki anti simetrik gerginin arasındaki bağıntı eylemsizlikle açıklanabilir ve gergi dördüncü dereceden olmalıdır;[1] Bu denklemdeki L ve ω herhangi bir boyutta doğruluğunu korur. Bu denklem geometrik matematiksel işlemlerde de görülür L ve ω bu sefer ortak vektörlerdir ve eylemsizlik arasında bir bağlantı oluşturur.
Göreceli mekanik ve göreceli açısal momentumda parçacıklar antisimetrik ikinci dereceden gergi ile ifade edilirler; Dört vektör dilinde dört yer X ve dört momentum P yukarıda ifade edilen L yi parçacıkların kütle merkezi hareketiyle yok ederler. Yukarıda anlatılmış olan her durum için çoklu parçacıkların olduğu bir sistemdeki açısal momentum oradaki her parçacığın ayrı açısal momnetumunun toplamına eşittir.
Kuantum mekaniğinde açısal momentum[değiştir | kaynağı değiştir]
Kuantum mekaniğindeki açısal momentum klasik fizikte anlatılmış olan açısal momentumdan biraz daha farklıdır. Göreceli kuantum mekaniğinde ise neredeyse bağlantıları kalmaz hale gelir çünkü açısal momentum artık tensörel çarpım haline gelmiştir.
Dönüş,orbital ve toplam açısal momentum[değiştir | kaynağı değiştir]

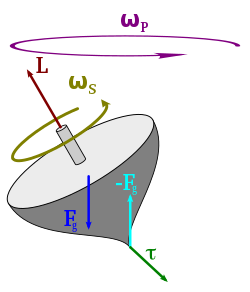
Sol: "Dönüş" açısal momentumu S cismin her bölgesindeki açısal momentumu belirtir.
Sağ: Açısal momentumunL herhangi bir eksendeki durumu,
Ūst: Anlık eylemsizlik I ve açısal hız ω (L her zaman paralel değildir ω),[2]
Alt: momentum p Yarıçapa göre r eksenden.
klasik açısal momentum tanımı; kuantum mekaniği ile daha ileriye taşınabilir. r nin yerine kuantum yer işlemcisi, p nin yerine momentum işlemcisi konulur. L ise bir işlemci haline dönüşür ve orbital açısal momentum işlemcisi adını alır.
Ancak, kuantum fiziğinde bir başka açısal momentum türü vardır ve ismi dönüş açısal momentumudur ve S ile gösterilir. Neredeyse her element parçacığın dönüşü vardır. Dönüş genel olarak bir eksen üzerinde dönüş yapma olarak tanımlanır ancak bu eksik ve yanlış anlaşılma yaratan bir resimdir. Dönüş parçacıkların doğası olan bir olaydır ve orbital açısal momentumdan farklıdır. Her element parçacığın kendine ait dönüş özelliği vardır örneğin elektronların dönüşü her zaman 1/2 dir. Fotonların ise 1 dir.
Sonuç olarak toplam açısal momentum J, dönüş ve orbital açısal momentumun her parçacık için toplamını ifade eder. (bir parçacık için J= L + S). Açısal momentumun korunumu J için geçerlidir ancak L veya S e işlemez. Toplam korunduğu sürece açısal momentum S ve L arasında artıp azalabilir.
Nicemlenim[değiştir | kaynağı değiştir]
Kuantum mekaniğinde açısal momentum nicem bir yapıya sahiptir, yani sürekli olarak değişime uğrayamaz yalnız istenilen miktarlarda kuantum sıçramaları yapabilir. Herhangi bir sistem için aşağıda verilmiş uygulamalar her zaman geçerlidir. düşürülmüş Planck sabiti, herhangi bir yön vektörüdür x, y, z gibi.
| Yapılan hesaplama... | Olabilecek sonuçlar... |
| or | |
| () |
, burada |
| or | , burada |

Düşürülmüş Planck sabiti normal standartlarda 10−34 J s dir. Bu sebepten ötürü açısal momentumu nicem oranı mikroskobik cisimleri etkileyemeyecek kadar küçüktür. Ancak mikroskopik sistemlerde oldukça önemlidir. Örneğin kimyada işlenen elektron katman ve tabakalarında açısal momentumun nicemlenimlenmesi çok önemlidir. Açısal momentumun nicemlenimlenmesi ilk olarak Niels Bohr tarafından Bohr atom modelinde ortaya sunulmuştur.
Kararsızlık[değiştir | kaynağı değiştir]
formülünde altı adet işlem elemanı bulunmaktadır. Bunlar; yer işlemcileri , , ve momentum işlemcileri , , . Heisenberg belirsizlik kuramlarına göre formülümüzde bulunan altı işlem elemanının kesin değerlerinin hepsi için aynı anda bulunması mümkün değildir. Bu sebeple bir parçacığın açısal momentumunu bulurken bazı kısıtlamalarla karşılaşırız. Yapılabilecek en tutarlı hesaplamalar tek bir eksen ve düzlem üzerindeki açısal momentum vektörünün yön ve değerini bulmaktır. Belirsizlik yasasının ifade ettiği gibi açısal momentum işlemcisinin değişik bileşenleri bir arada bulunamaz örneğin .
Dönüş üretebilen toplam açısal momentum[değiştir | kaynağı değiştir]
Yukarıda anlatıldığı gibi klasik mekanikteki açısal momentum L ile ifade edilir ancak toplam açısal momentum J daha farklı ve basit bir yolla dönüş yaratan[3] olarak ifade edilir ve işlemcisi; dönüş işlemcisidir ve her sistemde dönüşü ifade eder açısı ile ekseninde.
Açısal momentum işlemcisi ve dönüş işlemcisi arasındaki bağıntı lie matematiği ve lie grupları ile ifade edilebilir. Açısal momentum ve dönüş arasındaki bağıntı Noether teoreminde gösterilmiştir ve açısal momentumun fizik kuralları gereğince korunduğunu ispatlamıştır.
Elektrodinamikte açısal momentum[değiştir | kaynağı değiştir]
Yüklü bir parçacığın elektromagnetik alandaki hareketleri standart kabul edilen momentuma uymaktadır P. Standart açısal momentum L = r × P momentumu değişmez ölçülü değildir. Hatta fiziksel momentum olarak kabul edilen kinetik momentumUN SI birimi; e parçacığın elektrik yükü, A ise elektromagnetik alanın magnetik vektör potansiyelidir. Değişmez ölçülü açısal momentum, kinetik açısal momentum olarak da bilinir, şu formülle bulunur; Kuantum mekaniği ile ilgili bağlantılar kanonik yerdeğişim bağlantıları (canonical commutation relations) bulunmaktadır.
Kaynakça[değiştir | kaynağı değiştir]
- ^ Synge and Schild, Tensor calculus, Dover publications, 1978 edition, p. 161. ISBN 978-0486636122.
- ^ R.P. Feynman, R.B. Leighton, M. Sands (1964). Feynman's Lectures on Physics (volume 2). Addison–Wesley. ss. 31-7. ISBN 9-780-201-021172.
- ^ Littlejohn, Robert (2011). "Lecture notes on rotations in quantum mechanics" (PDF). bohr.physics.berkeley.edu. 26 Ağustos 2014 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 13 Ocak 2012.
- Cohen-Tannoudji, Claude; Diu, Bernard; Laloë, Franck (2006). Quantum Mechanics (2 volume set bas.). John Wiley & Sons. ISBN 978-0-471-56952-7.
- Condon, E. U.; Shortley, G. H. (1935). "Especially Chapter 3". The Theory of Atomic Spectra. Cambridge University Press. ISBN 0-521-09209-4.
- Edmonds, A. R. (1957). Angular Momentum in Quantum Mechanics. Princeton University Press. ISBN 0-691-07912-9.
- Jackson, John David (1998). Classical Electrodynamics (3. bas.). John Wiley & Sons. ISBN 978-0-471-30932-1.
- Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6. bas.). Brooks/Cole. ISBN 0-534-40842-7.
- Thompson, William J. (1994). Angular Momentum: An Illustrated Guide to Rotational Symmetries for Physical Systems. Wiley. ISBN 0-471-55264-X.
- Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5. bas.). W. H. Freeman. ISBN 0-7167-0809-4.



























































