Lagrange mekaniği

Lagrange mekaniği, klasik mekaniğin yeniden formüle edilmesidir. İtalyan-Fransız matematikçi ve astronom Joseph-Louis Lagrange tarafından 1788’de geliştirilmiştir.
Lagrange mekaniğinde, parçacıkların ve parçacık sistemlerinin hareketleri ve gezingeleri Lagrange denklemlerinin iki formundan birinin çözülmesiyle bulunur. Birinci tip Lagrange denklemleri,[1] parçacıkların hareketlerindeki kısıtlamaların, Lagrange’in kalkülüste de sık kullanılan Lagrange çarpanı[2][3] yöntemi kullanılarak ifade edilmesidir. İkinci tip Lagrange denklemlerinde ise hareket kısıtlarını, sistemin yapısına uyacak makul genelleştirilmiş koordinat[1][4] seçimi ile direkt olarak sistem denklemlerine dahil etmek üzerine kuruludur. İki durumda da matematiksel bir fonksiyon olarak tanımlanan, Lagrange’in sistem hakkında verdiği bilgilerden faydalanılır. Lagrangian, genelleştirilmiş koordinatların, onların türevlerinin (genelleştirilmiş hızlar) ve zamanın bir fonksiyonudur.
Lagrange mekaniğinde dikkat edilmesi gereken husus; yeni bir fiziğin ortaya atılmıyor oluşudur. Keza, Lagrange mekaniği Newton mekaniğinden[5] daha sığ bir kapsama sahiptir çünkü Newton mekaniği korunumlu olmayan sürtünme gibi kuvvetleri de içerir. Ancak bu tip kuvvetlerin doğru ifade edilmesi için hareketi kısıtlayan kuvvetlerin de sistem denklemlerinde ifade edilmesi gerekir ve kartezyen koordinat sistemi haricindeki koordinatlar bu yönteme pek uygun değildir. Ancak, Lagrange mekaniğindeki yöntemler ile kısıtlayıcı kuvvetlerin ve korunumsuz kuvvetlerin ekstra karmaşık denklemler yaratması önlenebilir. Lagrange mekaniği bu açıdan, korunumlu kuvvetlerin etki ettiği ve iç kuvvetler ile ilgilenmediğimiz sistemlerde çok etkilidir ve kartezyen koordinat harici istediğimiz koordinat sistemini kullanmamızda bize kolaylık sağlar. Ayrıca bazı korunumsuz kuvvetleri de göz ardı etmemize olanak tanıyabilir. Dolayısıyla, kontak noktalarındaki ve yapısal sistemlerle ilgilenilmeyen ve sadece genel dinamiğin ve hareketin önemli olduğu sistemlerde Lagrange mekaniği kullanımı çok etkilidir.
Genelleştirilmiş koordinatlar sistemin serbestlik derecesine göre istenildiği gibi seçilebilir. Ancak Lagrange mekaniğinin kolaylıklarından etkin bir şekilde faydalanmak için, sistemdeki simetrileri ve geometrik kısıtları ve özellikleri dikkate alarak uygun seçimler yapmak gerekir. Böylece matematiksel model ve denklemler önemli oranda basitleşir.
Lagrange mekaniği uygulama açısından kolaylıklarının yanında, teorik olarak doğadaki korunum yasaları yani fiziksel işleyiş hakkında da bize önemli bilgiler verir. Korunan her fiziksel değişken ve onların simetrisi üzerine kurulu olan bu bilgi Noether teoremi ile daha da genelleştirilmiştir. Bu teori aynı zamanda minimum eylem prensibi[6] ile de yakından ilişkilidir. Yine, Lagrange mekaniği, sadece denge (dinamik-statik-kaotik) problemlerine odaklandığından daha sığ kalmaktadır.[7] Ayrıca, Lagrange mekaniği, sadece holonomik kısıtları olan sistemlere uygulanabilmektedir çünkü formülasyon holonomik olmayan kısıtlar için çalışmamaktadır. Örneğin,[8] integrallenebilir olmayan kısıtlayıcı denklemler (hareket kısıtları hakkındaki denklemler), Coulomb sürtünmesi gibi doğrusal olmayan karmaşık korunumsuz kuvvetler ve aralıklar ile eşitsizliklerle tanımlanmış hareket kısıtlarını tanımlayan denklemlere sahip sistemlerde Lagrange mekaniği etkin olamamaktadır. Holonomik olmayan sınırlamalar özel analiz gerekmektedir. Bu durumlarda Newton mekaniği veya başka yöntemler kullanılabilir zira bu durumlarda Lagrangian’in temelini oluşturan enerji terimlerinin ifadelerinde sıkıntılar yaşanmaktadır. Çünkü bu terimler kuvvet ve yola bağlı terimlerin integralleri ile ifade edilmektedir.
Daha önce de bahsedildiği gibi, Lagrange formülasyonu pratikteki uygulama kolaylıklarının yanı sıra, mekanik fiziği ve doğanın mekanik davranışını anlamamızda bize derin bir bakış açısı sağlar. Kuantum mekaniğinde, Planck sabiti ile ilişkili olan etki ve kuantum fazlarda, minimum eylem prensibi dalga yayılımı ve dalga yayılım denklemleri ile anlaşılabilmekte ve benzer mekanik yaklaşımlar bu gibi apayrı alanlarda da türetilebilmektedir. Lagrangian eğer simetri altında değişmez ise, sonuçta ortaya çıkan hareket denklemi de simetri altında değişmezdir. Bu karakteristik de özel görelilik ve genel görelilik teorisindeki açıklamalar için çok önemlidir. Minimum eylem prensibi, Lagrange formülasyonları gibi konular Noether teoremi ile yakından ilişkilidir ve bu teorilerin sonucunda daha önce sadece gözleme veya basit derivasyonlara dayalı kalmış olan korunum yasaları ve korunan nicelikler; inceleme altındaki fiziksel sistemin sürekli simetrileri ile ilişkilendirilebilmiştir. Dolayısıyla, bu algı; momentum, kütle gibi temel korunum sahibi niceliklerin ötesinde her sistem için farklı ve daha genel korunum ifadeleri yazabileceğimizi ortaya atmış ve bunların nasıl türetileceği, hangi durumlar altında kullanılabileceği hakkında bize bilgi vermiştir. Lagrange mekaniği ve Noether teoremi ayrıca komutatörleri içeren birinci kuantizasyonlar için doğal bir biçimcilik ortaya koymuştur ve bunu belli terimler ile Lagrangian ile türetilmiş hareket denklemleri arasında göstermiştir.
Lagrange mekaniği, Newton mekaniğinin uygun olmadığı, çok vakit aldığı veya etkili sonuç çıkartamadığı yerlerde hem teorik fizikte hem de pratik mekanik uygulamalarda çok etkilidir. Ayrıca minimum eylem prensibi ile yakından ilişkili olduğundan optimizasyon problemlerinde de kullanılabilmektedir. Mekanik biliminde, ikinci tip Lagrange denklemleri birinci tipe göre çok daha sık kullanılmaktadır.
Giriş[değiştir | kaynağı değiştir]
Lagrange mekaniğinin gücü, hareketi kısıtlanmış mekanik sistemlerde, bu kısıtları etkili ifade ederek sistem çözümüne dahil edebilmesinden gelir. Aşağıdaki örnekler, konseptleri ve terminolojiyi anlamada etkili olacaktır.
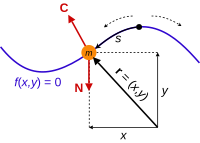
Rijit bir eğimli yolu ifade eden bir telde hareket eden bir küreyi düşündüğümüzde, ağırlığın etkili olduğu 2 boyutlu uzayda; hareket kısıtları f(r) = 0 formunda ifade edilebilir. Burada kürenin hareketi r = (x(s), y(s)) olarak yazılabilir ve s eğrisel uzunluk olarak tanımlanır (her eğri, yay parçaları olarak ifade edilebileceğinden, dsi diferansiyel yay uzunluğu, si de yay boyuncaki koordinat olarak tanımlayabiliriz). Eğride her noktadaki x ve y birbirine bağımlı olduğundan, aslında x ve y gibi iki koordinat tanımlamak yerine tek bir s koordinatı hareketimizi tanımlamamıza ve kısıtlarımızı ifade etmemize yetecektir. Çünkü hareket kısıtlarını ifade eden denklemler x ve y arasında bir bağıntı vermekte ve serbestlik derecesini düşürmektedir. Böylece x ve y den biri bilindiğinde öbürü bulunabilir.
Hareket kısıtlarının bir sonucu olan kısıtlayıcı kuvvetler ise, hareketin kısıtlandığı yönde uygulanan kuvvetlerdir veya başka bir açıdan, kürenin istenilen yolda kalmasını sağlayan kuvvetlerdir. Ayrıca ağırlık da, kısıtlayıcı olmayan bir kuvvet olarak küreye etki etmektedir.
Eğer telin şekli zamanla değişiyorsa (örneğin esneme ile), o zaman kısıtlayıcı denklemler ve pozisyon zamana bağlı olarak da değişmeye başlar. Çünkü koordinatlar zamanla değişmektedir. Zaman, koordinat tanımlarında örtülü olarak kalırken, kısıtlayıcı denklemlerde açık olarak gelir.
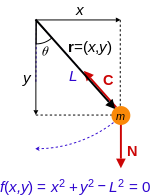
Başka bir ilginç 2 boyutlu örnek ise kaotik/düzensiz bir dinamiğe sahip olan çift sarkaçtır (yine yer çekimi altında). Bir sarkaçın uzunluğu L1 ve diğerinin uzunluğu ise L2 olsun. Her bir kütle hareketlerinin kısıtlanmasını ifade eden denklemlere sahiptir. Her sarkacın kısıtlayıcı denklemi vardır,
Kütlelerin pozisyonları ise,
olarak ifade edilebilir.
θ 1 ve θ 2 belli bir referansa göre sarkaçların açısını ifade eder. Her sarkaç, kısıtlardan ötürü birer koordinatla ifade edilebilir. Çünkü bu kısıtlar mekansal koordinatları (2 tane) birbirine bağlar.
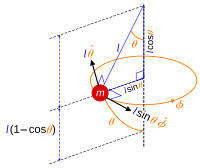
3 boyutlu bir örnek olarak, küresel eksenlerde hareket eden sarkaç örnek verilebilir. Sarkacın uzunluğu l ve sarkaç her yönde serbestçe sallanacak şekilde ağırlığının etkisine bırakılmış durumdadır. Bu durumda, hareket kısıtlanması şu şekilde ifade edilebilir;
Kütlenin pozisyonu ise daha önce s ve θ değişkenlerinin kullanıldığı gibi genel koordinatlarda şu şekilde ifade edilebilir;
ve burada (θ, φ) çifti küresel kutup açılarını ifade eder çünkü kütle bir kürenin yüzeyinde hareket edermişçesine davranır aynı zamanda küresel koordinatlarda tanımlanabilir ve aynı bu durumda olduğu gibi, yarıçapın sabit olduğu bir kürenin denklemi de kısıtımızı ifade eder. Böylece 3 koordinat yerine 2 koordinat bilgisi yeterli olmaktadır.
Özellikle sarkaç gibi sistemler, salınım hareketi yaparlar çünkü yükleme, pozisyon değişkeni olan açının sinüsel bir fonksiyonudur. Böylece basit harmonik osilatörler Lagrange mekaniği ile yine rahatça analiz edilebileceği anlaşılabilir. Ayrıca, bu tip enerji metotları denk sistemler bulmak, çoklu serbestlik dereceye sahip sistemlerin analizi gibi problemlerde ciddi işe yaramaktadırlar çünkü yazılımsal olarak adapte edilebilmeleri kolaydır. Dolayısıyla, bağlanmış harmonik osilatörler (çift sarkaç, üçlü sarkaç gibi) özellikle Lagrange dinamiği metotları ile incelenir.
3 boyutlu uzayda yer alan N partikül için, pozisyon vektörleri 3 değişkenli vektör fonksiyonları olarak şöyle ifade edilebilir;
Dolayısıyla, her bir parçanın net pozisyonunu bilmek için 3N kadar koordinata ihtiyacımız vardır. Zaten bir vektör uzayında da bir noktanın genel ifadesi r = (x, y, z). fonksiyonu ile yapılır.Bu partiküllerden herhangi birisi veya birkaçı holonom kısıtlara tabi tutulursa, kısıt ifadesi f(r, t) = 0 şeklinde yazılabilir. Bu, herhangi bir anda partiküllerin pozisyonları birbirlerine bağlanmaya başlar ve bağımsız olmaktan çıkarlar. Eğer sistemde C kadar kısıtlayıcı var ise, bunların her birinin fonksiyonel ifadesi için,
Fonksiyon eşitlikleri kullanılır ve her bir denklem bir koordinat ihtiyacını eler. Dolayısıyla bağımsız koordinatların sayısı n = 3N − C kadardır. Unutulmamalıdır ki bağımlı koordinatlar kullanılarak yapılan hesaplar modeli karmaşıklaştıracaktır.
Dolayısıyla, partikülleri veya sistemi tanımlamamız için n tane koordinata ihtiyacımız bulunmaktadır. Her pozisyon vektörü istenilen n elemanlı genelleştirilmiş koordinat setine dönüştürülebilir. Ve uygun bir şekilde q = (q1, q2, ... qn) olarak ifade edilebilir. Dolayısıyla pozisyonlar şu şekilde ifade edilebilir;
Böylece, pozisyonlar, genelleştirilmiş koordinatların fonksiyonu olarak karşımıza çıkar çünkü pozisyon değişkenlerini herhangi bir sete dönüştürebiliriz.
Genelleştirilmiş koordinatların birinci türevine genelleştirilmiş hızlar denir ve her partikül için hız vektörlerinin dönüşümleri;
(Noktalar Newton notasyonu olarak zamana göre türevi ifade eder.)
Burada unutulmamalıdır ki hız, pozisyonun toplam diferansiyelidir. Veya basitçe rk olarak tanımladığımız fonksiyonun zamana göre türevidir ve q da zamana bağlı olduğu için zincir kuralı kullanılır.
Önceki örneklerde, biri eğer her kütlenin hareketini partikül olarak inceleyecek basitleştirmeler yapabiliyorsa, Newton mekaniği zamana bağlı olarak değişen kısıtlayıcı kuvvetlerin (partikülleri kısıtlanmış hareket patikasında tutmaya yarayan kuvvetler) zamana göre değişimi ile uğraşmayı gerektirir (telin küreye uyguladığı kuvvet, çekme kuvvetinin sarkaca aktardığı kuvvet gibi).Aynı problem için Lagrange mekaniği, bizim partikülün aldığı yola bakarak uygun bir genelleştirilmiş koordinat seçmemize dayanır. Bu seçimlerdeki koordinatlar bağımsız olmalıdır ve hareketi tamamen karakterize edebilmelidir. Hareketin tamamen serbest olduğu koordinatlar seçilirse, kısıtlayıcı denklem ve kuvvetlerin işin içine girmesine gerek kalmaz. Örneğin x-y düzleminde tel üzerindeki bir kürenin hareketi her an tanjantlara dik olarak kısıtlanmıştır ama tek bir s koordinatı seçilirse, zaten o koordinat yolun ve hareketin kendisini tanımladığı için ve hareketin olmadığı yerlerde sıfır olduğu için ekstra kısıt ifadelerine gerek kalmaz. Böylece, kısıtların partiküller üzerindeki direkt etkisi hesaplanmadan daha az denklem çözülerek sistem modellenebilir.
Lagrangian'ın tanımı[değiştir | kaynağı değiştir]
Lagrange mekaniğindeki temel nicelik Lagrangian fonksiyonudur. Bu fonksiyon, sistemin dinamik davranışı hakkında önemli bilgiler barındırır. Ancak, her fiziksel sistem için tek bir Lagrangian ifadesi türetmek mümkün değildir. Esasen, Euler-Lagrange denklemlerini fiziksel yasalarla uyumlu bir şekilde türetebilecek her fonksiyon Lagrangian olarak ele alınabilir. Ancak yine de, bazı gruplanabilecek sistemler için genel Lagrangian ifadeleri oluşturmak mümkündür.
Örneğin, görelilik etkilerin ihmal edilebileceği sistemler için Lagrangian;[9]
olarak ifade edilebilir. (mekanikte en sık karşılaşılan ifade budur, ancak bunun tüm sistemler için genel bir ifade olmadığına dikkat edilmesi gerekir. Farklı fiziksel yasaların da işin içine girmesiyle değişmesi gerektiğini unutmamak gerekir.) Burada T, sistemin toplam kinetik enerjisini ve V ise potansiyel enerjisini ifade eder. Lagrangian’ın birimi, seçilen enerji birimleriyle aynıdır.
Kütleleri m1, m2, ..., mN olan N parçacıktan oluşan bir sistem için toplam kinetik enerji her bir parçacığın kinetik enerjisi toplanarak bulunabilir. (Enerji metodlarındaki toplanabilme özelliği bu açıdan çok güçlüdür.) Her parçacığın enerjisi sistemin hareketine göre şöyle tanımlanabilir;[10]
Burada, işaretlerin doğru verilmesi için noktasal çarpım kullanılmıştır. Yani kinetik enerji ne olursa olsun pozitif bir ifadedir. Bu ifadeye göre, kinetik enerji sadece hızların yani vk terimlerinin bir fonksiyonudur. Kinetik enerji rk'ya yani parçacıkların pozisyonlarına ve zamana bağlı değildir. Dolayısıyla T(v1, v2, ...) olarak ifade edilebilir. Ancak, yukarıdaki genelleştirilmiş koordinat ve hız ifadeleri göz önüne alındığında, özellikle zamana bağlı bir değişim söz konusu ise; genelleştirilmiş koordinatlar çerçevesinde ifade edilen kinetik enerji genelleştirilmiş hızlara, koordinatlara ve pozisyon vektörleri zamana bağlı çarpanlar içeriyorsa zamana bağlıdır. Yani T = T(q, dq/dt, t) olarak daha doğru bir şekilde ifade edilebilir.
Potansiyel enerji V ise sistemdeki parçacıkların birbirleri ile olan ilişkilerini yansıtır. Başka bir deyişle, bir parçacığın diğer tüm parçacıklara ve dış etkilere göre ne kadar enerjisi olduğunu ifade eder. korunumlu kuvvetlerin etkisinden ötürü oluşan potansiyel enerji, sadece parçacıkların pozisyonlarına bağlıdır yani V = V(r1, r2, ...)’dir. Korunumlu olmayan kuvvetler için de uygun potansiyel enerji fonksiyonları türetilebilir. Ancak bu durumda işin içine hızlar da girmek zorundadır. Yani korunumsuz kuvvetler için V = V(r1, r2, ..., v1, v2, ...) olarak ifade edilebilir. Ayrıca dış bir fiziksel alan veya kuvvet zamana bağlı olarak değişiyorsa potansiyel enerji de bundan etkilenecektir. Dolayısıyla en genel haliyle; V = V(r1, r2, ..., v1, v2, ..., t) olacaktır.
Eğer potansiyel ve kinetik enerjilerden biri veya ikisi de zamana açık bir bağlılık gösteriyorsa (zamanla değişen kısıtlar, etkiler, çarpanlar veya sistem parametreleri) Lagrangian da zamana açık bir şekilde bağlı olacaktır. Yani L[q,dq/dt,t) olacaktır. Eğer potansiyel enerji ve kinetik enerji zamana göre değişmiyorsa bu durumda, Lagrangian, L(q, dq/dt) formunda olacaktır ve zamana açık bir bağlılık göstermeyecektir. Ancak zamana göre türev alındığı için zamana örtülü bir şekilde bağlı olacaktır. İki durumda da Lagrangian’ın zamana örtülü olarak bağlı olacağı kesindir (Genelleştirilmiş koordinatlar kullanılırsa).
Lagrangian’a ek olarak ayrıca, disipatif yani hareket süresince enerjiyi o an sistem içinde dönüştürülemez şekilde harcayan sistem elemanlarını göz önüne alarak çeşitli fonksiyonlar türetmek de mümkündür.
Göreli-mekanikde, L daha derin bir şekilde analiz edilip doğru ifade edilmelidir. Bunun için relativistik Lagrange mekaniğine bakılabilir. (Enerji ifadeleri artık daha farklı olacak ve dönüşümler, zamana bağımlılık farklı bir yapı gösterecektir.)
Hareket denklemleri[değiştir | kaynağı değiştir]
Newton mekaniğinde, hareket Newton Yasaları ile ifade edilir. Newton’un ikinci yasası F = ma her parçacığa uygulanır ve 3 boyutta hareket sahibi olanN parçacıklı bir sistem için 3N tane adi diferansiyel denklem pozisyonların bulunması için çözülür(ivmenin iki kere integrali alınarak).
Lagrange mekaniğinde ise, Lagrangian fonksiyonu hareket denklemlerini türetir. Hareket denklemleri, kısmi türev ∂/∂ içerse bile, denklemler yine de genelleştirilmiş pozisyon koordinatlarında çalışan adi diferansiyel denklemlerdir. Ayrıca zaman göre toplam türev ifadesi,d/dt örtülü türev alınmasını gerektirebilir.
İki çeşit hareket denklemi vardır. Biri kısıtlayıcı kuvvetleri ve hareketlerin kısıtlarını ifade eden denklemlerini işin içine katarken, diğeri bunları modellemenin dışında tutarak sadece kısıtlayıcı olmayan ve hareket sağlayan kuvvetleri genelleştirilmiş koordinatlarda inceler. Bu ifadeleri Lagrangian’a koyup gerekli denklemleri çözerek, sınır ve ilk değerleri katarak (hız ve pozisyon) parçacıkların pozisyonlarını zamana göre çözebilir ve sistemin zamana göre hareketini, değişimini bulabiliriz.
Birinci tip Lagrange denklemleri[değiştir | kaynağı değiştir]
3 boyutlu uzayda N parçacıktan oluşan ve C tane holonomik kısıta maruz kalan bir sistemin kısıtları yukarıda belirtildiği üzere, f2,..., fC gibi fonksiyonlarla ifade edilebilir ve sistemin dinamiği, Lagrangian L(r, dr/dt, t)'a bağlı olarak birinci tip Lagrange denklemleri ile şöyle ifade edilebilir;[11]
burada k = 1, 2, ..., N her bir parçacığı ifade eder ve bu denklemler sisteme dahil olan her eleman veya parçacık için çözülmek üzere bir denklem sistemi oluşturur. Ayrıca, her bir kısıtlayıcı denklem fi için birer Lagrange çarpanı λi bulunur. Ve bu indisler her bir vektörün her bir ilgili değişkene göre türevini ifade etmede kolaylık sağlar.
Burada dikkat edilmesi gereken, Lagrangian’ın her bir vektöre göre türevi alınmasından ziyade yine mekansal koordinatlara göre türev alındığı ve buradaki gösterimin kolaylık olduğudur.
Bu prosedür Newton yasalarıyla çözülebilecek 3N denklem sayısını kısıtlayıcı denklemlerin de işin içine girmesiyle 3N + Cye çıkartır. Çünkü N parçacık için 3 boyuttta – 3 pozisyonda 3N denklem vardır ve C kadar hareket kısıtlarını ifade eden denklem vardır. Ancak burada etkili olan nokta Lagrange çarpanlarıdır ve bu çarpanlar kısıtlayıcı kuvvetler hakkında bize çözüm sırasında bilgi verir. Bu metotta genelleştirilmiş koordinatlar veya kısıt denklemlerinin temel hareket denklemlerine katılması kullanılarak denklemleri elimine etme ihtiyacı yoktur. Kısıt denklemleri ekstra denklemler olarak Lagrange çarpanları ile ifade edilir ve sistem çözülür.
İkinci tip Lagrange denklemleri[değiştir | kaynağı değiştir]
Euler-Lagrange denklemleri veya Lagrange’ın ikinci tip hareket denklemleri[12][13] olarak adlandırılır. Değişim kalkülüsünün matematiksel bir sonucu olarak ortaya konmuştur. Bu sonuç fiziksel – mekanik sistemlerde de hem doğalarını anlamada hem de hareketlerini hesaplamada kullanılır.
Lagrangian’ın L(q, dq/dt, t) formulasyonu bu denkleme konduğunda her bir genelleştirilmiş koordinata karşılık bir denklem bulunur. Ve genelleştirilmiş koordinatlar eksenel koordinatlar – kısıtlar sayısı kadar seçildiğinden toplamda 3N-C kadar 2. Dereceden adi diferansiyel denklemi çözmemiz gerekir. Bu denklemler hareket kısıtlarını içermezler ve sadece kısıtlayıcı olmayan – hareketi gerçekleştiren kuvvetlerin modele katılması gerekir.
Bu metot, değişim kalkülüsündeki minimum değişim ve hareket prensibinin fiziksel bağlamda enerji olarak ifade edilebilecek bir değişim fonksiyonuyla etkili bir şekilde kullanımı ile ortaya çıkar.
Newton mekaniğinden Lagrange mekaniğine[değiştir | kaynağı değiştir]
Newton yasaları[değiştir | kaynağı değiştir]

Basitçe, Newton yasaları bir parçacık için en genel bir şekilde;
olarak ifade edilir. Burada a, ivme; pozisyonun 2. Türevidir. Bu sayede N parçacığa sahip bir sistemde her parçacığa bu prensip uygulanarak hareket denklemleri çıkartılır. F ise, parçacığa etkiyen toplam kuvvettir.
Üç mekansal koordinatta her bir parçacık için üç hareket denklemi ortaya çıkar. Ve bu denklemlerin her biri adi diferansiyel denklemdir. 3 boyutlu uzayda üç değişken içerecek sonuçlar, birer vektör olarak ifade edilebilir. Elbette, her bir çözüm ilk hız, ilk pozisyon gibi başlangıç değerlerine tabidir.
Newton yasalarının kartezyen koordinatlarda kullanımı çok rahattır. Ancak çoğu harekette (özellikle de eğrisel hareketlerde) kartezyen koordinat kullanımı zordur. Bu durumda kartezyen koordinatların uygun koordinatlara çevrilmesi ve denklemlerin bu şekilde ifade edilmesi gerekir. Ancak bu durumda da pozisyonların türevlenmesi gerektiği için hareket denklemleri karmaşıklaşır. Örneğin üç eğrisel koordinatta ξ = (ξ1, ξ2, ξ3), Newton yasası "Lagrange formunda"[14][15] şöyle ifade edilebilir;
Burada Fa, kartezyen uzaydan eğrisel uzaya geçişte, uzayların taban vektörlerinin değişmesinden ötürü değişen kuvvetlerinkarşıdeğişkeni a bileşenidir. Γa ise ikinci tip Christoffel sembolleridir. Burada bir parçacığın kinetik enerjisi;
olarak ifade edilebilir. gbc, eğrisel koordinat sisteminin metrik tensörün eşdeğişken bileşenidir.Her a, b, c, indisi 1,2,3 gibi değerler alır. Burada dikkat edilmesi gereken husus, eğrisel hareketin önemi vurgulandığından; bu koordinat sisteminin genelleştirilmiş koordinatlarla karıştırılmaması gerektiğidir.
Burada yapılan türetmeler Newton yasalarının fazlaca karmaşıklaştırılması olarak düşünülebilir. Ancak bu yöntemin de çeşitli avantajları bulunmaktadır. Christoffel sembolleri cinsinden ifade edilen ivme bileşenleri, yukarıda tanımlanan kinetik enerjinin türevleri alınarak ifade edilebilir ve böylece T gibi bir her referans yapısında aynı kalacak skalerin kolaylığı kullanılabilir. Zaten Lagrangian gibi enerji metodları da vektörlerin referanslara bağımlılığını elimine ederek işlemleri kolaylaştırma ihtiyacına dayanır (Bunu yaparken ise sistemin detaylarından feragat etmek durumunda kalırlar).
Eğer sistem üzerine etkiyen bir kuvvet yoksa, yani F = 0 ise, sistem ivmelenemez. Ya durur ya da hareketini değiştirmeden devam eder. Hareket durumu daha genel bir ifadeyle; doğru üzerinde sabit hızlı harekettir. Ancak bu, bildiğimiz anlamda doğru olmak zorunda değildir. Örneğin eğrisel koordinatlara geçtiğimizde (jeodezik koordinatlar) doğrular artık keseller olarak karşımıza çıkar. Dolayısıyla, eğrisel yüzeyler üzerinde hareket etmek üzere kısıtlanmış veya o şekilde dengeye gelmiş parçacıkların hareket denklemlerinin çözümü keselleri verir. Keseller uzayda iki genel nokta arasındaki en kısa uzunluğa karşılık gelen eğrilere verilen genel addır. Düzlemde ise bunlar basitçe doğrulardır. Dolayısıyla 3 boyutlu uzayda da keseller düz doğrulara karşılık gelirler. Dolayısıyla, serbest bir parçacık için, Newton’un 2. Yasası geometrik jeodezik denklemleri ile uyum halindedir ve keselleri takip eden serbest parçacıkların hareketlerini ifade etmede kullanılır. Burada en önemli nokta, kesellerin 3 boyutlu uzayda parçacıkların iki nokta arasında izleyeceği en kısa yolu ifade etmesidir. Eğer parçacıklar belli bir kuvvet altında kalırlarsa ivmelenirler ve bu nedenle jeodezik hareketten sapmaya başlarlar.
Uzayda noktalar arası en kısa yolları bulma fikri mekanikte doğal bir merak konusudur. Özellikle enerjinin tanımından sonra mekanik sistemlerin minimum enerjiyle amaçlarını gerçekleştirmeleri önem kazanmıştır. Bu nedenle, değişimler hesabı (kalkülüs) metotlarının mekaniğe uygulanması ile yukarıda bahsedilen sonuçlar elde edilmiştir. Brachistochrone problemi (sabit ivme altında en kısa yol) gibi önemli konular değişimler hesabı sayesinde açıklığa kavuşturulmuştur. [[Johann Bernoulli|Jean Bernoulli)), Leibniz, Daniel Bernoulli, L’Hôpital gibi bilim insanları bu konu üzerine çalışmış ve farklı zamanlarda benzer çözümler bularak katkı sağlamışlardır.[16] Newton’un kendisi bile değişimler hesabı prensiplerini o zamanlarda düşünmeye başlamıştı.[16] Hatta yukarıda bahsedilen eğri uzunluğu gibi kavramları tanımlayıp, onların türevlerine bakarak düzlemde en kısa yolu ifade eden doğruları eğrilere nasıl adapte edebileceğini düşünmekteydi. Bu fikirler üzerine varyasyonel prensipler Fermat, Maupertuis, Euler ve Hamilton gibi bilim adamları tarafından net bir şekilde ortaya kondu. Ayrıca, uzay-zaman gibi 4 boyutlu uzaylara da uygun şekilde genelleştirilerek Einstein’ın genel görelilik teorisine katkı sağladı. Bahsedildiği gibi uzay eğrisel olarak, zamanda büküldüğünde oluşan uzay zaman boyunca; serbest parçacıklar, düzlemde doğruya karşılık gelecek şekilde jeodezik hareket yaparlar.[17]
Ancak, Newton mekaniğinde, parçacıkların hareketlerini tam olarak modelleyebilmek için üzerlerine etkiyen kuvvetleri F bilmek gerekir. Genel bir harekette bu kuvvet, hareketi çeşitli eksenlerde kısıtlayan veya kısıtlamayan kuvvetlerin birleşimidir. Kısıtlayıcı kuvvetleri C, kısıtlayıcı olmayan ve hareketi direkt sağlayan kuvvetlere ise N dersek;
olarak ifade edebiliriz.
Kısıtlayıcı kuvvetler karmaşık olabilir ve yola göre değişkenlik gösterebilir. Kısıtlanan mekanik sistemlerde genelde hareket yolu olabildiğinden çoğunlukla zamana (veya harekete) bağlı olurlar. Bu durumlarda eğrisel koordinatlar bağımsız değillerdir ve çeşitli kısıt denklemleri ile bağlıdırlar.
D'Alembert prensibi[değiştir | kaynağı değiştir]

Analitik mekaniğin ilk temel sonucu olan D’alambert prensibi 1708’de Jacques Bernoulli tarafından ortaya statik dengeyi anlamak için atıldı ve D’Alambert tarafından 1743’de dinamik problemlerini çözmek için geliştirildi.[18]
Bu prensip, N parçacık için şu denklemi tanımlar;[10]
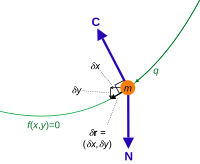
Burada, δrk,sanal yer değiştirmeleri tanımlar. Sanal yer değiştirme ise, sistem konfigurasyonundaki kısıtlar (hareket ve kuvvet bazında) ile uyumlu olan, diferansiyel (çok küçük) değişimlere denir.[19] Değişimler çok küçük olduğundan, r, kısıtlanmış hareket eksenlerinde tanımlansa bile kısıtlayıcı kuvvetlerin etkisini bozmaz. Bu sayede her tip hareket incelenebilir ve denklemlere katılabilir. Burada kısıtlayıcı veya değil her kuvvetin sanal yer değiştirmeler boyunca yaptığı işlere sanal iş adı verilir.
Kısıtlayıcı kuvvetler her parçacığın hareketine dik yönde etki eder. (En genel haliyle uzaylarda hareketi tanımlamak için n boyutlu uzay ise n kadar birbirine dik vektör ifadesi gerektiği için oluşacak tüm kısıtlayıcı kuvvetlerin bileşkesi harekete dik yönde olacaktır. Böylece o yöndeki vektör boyunca gerçekleşecek hareket iptal olacaktır.) Kısıtlayıcı kuvvetler tarafından gerçekleştirilen toplam sanal iş bu nedenle hareket boyunca sıfırdır (Noktasal çarpımdan ötürü).[20]
dolayısıyla;
eşitliği elde edilir.
Bu nedenle, D’Alambert prensibi bize kısıtlayıcı olmayan kuvvetlere odaklanmamızı sağlar ve kısıtlayıcı kuvvetleri hareket denklemlerinden çıkartır.[21][22] Hareket denklemlerinin bu formu aynı zamanda birbirinden bağımsız olarak sistemle uyumlu genelleştirilmiş koordinat seçimine de direkt uyum sağlar. Ancak, yine de bu denklemleri her parçacık ve genelleştirilmiş koordinat için ifade edip bağıl bir şekilde çözmek gereklidir.
D’Alambert prensibiden çıkartılan hareket denklemleri[değiştir | kaynağı değiştir]
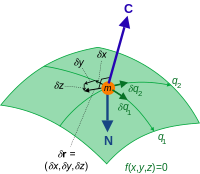
Eğer k parçacığının üzerinde kısıtlar varsa, kartezyen uzaydaki rk = (xk, yk, zk) pozisyonundaki koordinatlar kısıt denklemleri ile birbirine bağlanır. Burada sanal yer değiştirmeler; δrk = (δxk, δyk, δzk) olarak tanımlanabilir. Bu koordinatları hareket denklemleri içerisinde kısıt denklemleri ile uğraşmamak için genelleştirilmiş koordinatlara sanal yer değiştirme olarak dönüştürebiliriz. Sanal yer değiştirmeler diferansiyel boyutta olduğu için toplam diferansiyel formunu kullanabiliriz. Yani türevleri kullanarak yine işimizi analitik olarak kolaylaştırabiliriz.[23]
Bu sayede direkt δrkyı kullanarak yaşayacağımız sorunları, genelleştirilmiş koordinatları kullanarak ve sanal küçük hareketlerin aslında diferansiyel (türev ile ilintili) olduğu gerçeğini kullanarak hareket denklemlerini çıkarmayı kolaylaştırabiliriz.
Unutulmamalıdır ki, burada zamana göre kısmi türevin yine küçük bir zaman artışıyla çarpımı yoktur. Burada artağan bir zamandan ziyade anlık bir zamandaki ufak-diferansiyel yer değiştirmeler söz konusudur dolayısıyla türevlemeler ve artışlar yer değiştirmeler cinsindendir.
D’alambert prensibinin birinci terimi, kısıtlayıcı olmayan Nk kuvvetlerinin diferansiyel δrk boyunca yaptığı sanal işi kapsar. Ve genel olarak bu terim genelleştirilmiş kuvvetler analojisiyle ifade edilebilir(genelleştirilmiş koordinatlar boyunca etkiyen);
dolayısıyla,
şeklinde ifade edilir.
Burada yapılan genelleştirilmiş koordinatlara yapılan dönüşümün yarısını içerir. Geriye, ivmeleri içeren terimin genelleştirilmiş koordinatlara dönüştürülmesi kalır. Bu hemen görülebilir değildir. Yukarıda bahsedilen Newton Yasalarının Lagrange formu, kinetik enerjinin genelleştirilmiş koordinatlara ve hızlara göre kısmi türevini kullanarak istenilen sonucu verebilir;[24]
Bu sayede D’alambert prensibini istediğimiz şekilde genelleştirilmiş koordinatlarda şu şekilde yazabiliriz;
Dolayısıyla artık sanal yer değiştirmeler genelleştirilmiş koordinatlar cinsinden yapılabilir. δqjler birbirlerinden bağımsız ve sıfırdan farklıdır. Çünkü herhangi bir zaman anında belirli bir yer değiştirmeden bahsediliyor. Bu nedenle δqjların katsayıları sıfıra eşitlenebilir. Bu katsayılar da özellikle statik durumlar için genelleştirilmiş kuvvetler olarak adlandırılabilir. Bu sayede, esasen Lagrange denklemlerini[25][26] veya genelleştirilmiş hareket denklemlerini[27] elde etmiş oluyoruz.
Lagrange Denklemleri ; Euler-Lagrange Denklemleriyle karıştırılmamalı, burada enerji terimleri yerine genelleştirilmiş kuvvet terimleri yer alır.
Bu denklemler, kısıtlayıcı olmayan kuvvetler altında bize Newton’un yasaları ile aynı sonucu verir. Yukarıdaki denklemlerdeki genelleştirilmiş kuvvetler sadece kısıtlayıcı olmayan kuvvetlerden türetilmiş ve kısıtlayıcı kuvvetler dışarıda D’Alambert’in sanal iş prensibi sayesinde bırakılmıştır ve ihtiyaç yoktur. D’Alambert prensibi kuvvetlerin korunumluluğu üzerinde geneldir. Bu kuvvetler D’Alambert prensibini sağladığı sürece korunumsuz olabilir.[28]
Hamilton prensibi ile Euler-Lagrange denklemleri[değiştir | kaynağı değiştir]

Korunumlu olmayan kuvvetler, pozisyon ve zamana ek olarak, korunum kavramının tanımı gereği hıza da bağlıdır. Dolayısıyla, pozisyona ve hızlara bağlı bir potansiyel enerji fonksiyonu tanımlamak mümkündür. Eğer genelleştirilmiş kuvvetler bir V potansiyelinden şu şekilde türetilebiliyorsa;[30][31]
ve Lagrangian’ı L = T − V olarak tanımlayıp bunu Lagrange denklemlerine eşitlersek ikinci tip Lagrange denklemlerini veya Euler-Lagrange denklemlerini elde ederiz;
Ancak, Euler-Lagrange denklemlerinde korunumsuz kuvvetler, sadece onları ifade edebilecek bir potansiyel fonksiyonu bulunursa ifade edilebilir. Dolayısıyla Lagrange denklemleri potansiyel içermediği, kuvvet içerdiği için Euler-Lagrange denklemlerinden daha geneldir. Çünkü Euler-Lagrange denklemlerinde kuvvetleri korunumlu veya korunumsuz; potansiyel fonksiyonları olarak ifade etmeye çalışıyoruz. Ve böyle bir potansiyel bulunamazsa EL denklemleri o kuvvetleri kapsayamıyor.
Euler-Lagrange denklemleri değişim hesabı metotlarıyla bulunabilir. Lagrangian fonksiyonunun değişimi şöyle ifade edilebilir;
Bu tanım, Lnin toplam diferansiyeline çok benzerdir. Ancak sanal yer değiştirmeler ve onların zamana göre türevleri sadece diferansiyel terimlerle yer değiştirir (del operatörü ile, belli bir büyüklük olarak ifade edilirler). Ayrıca, sanal yer değiştirme’nin tanımına uyacak şekilde, zaman artışı bu tanımda yer almamaktadır. Onun yerine genelleştirilmiş koordinatların zamanda bir ana göre ifade edilir ve türevlerden ziyade diferansiyel terimlerin çarpımları kullanılır. Zaman göre uygulanan bir parçalı integral yöntemi genelleştirilmiş koordinatların türevlerini yani δqjı ∂L/∂(dqj/dt) terimine dönüştürür. Diğer bir deyişle d(δqj)/dtnın δqjya dönüşümü gerçekleştirilir. Buradan, bağımsız sanal yer değiştirmelerin Lagrangian fonksiyonunun türevi ile türetilebileceği ortaya çıkar;
Eğer δqj(t1) = δqj(t2) = 0 koşulu her j terimi için doğru oluyorsa, integrali alınmayan terimler sıfır olur. Buna ek olarak eğer δLin zamana göre integrali sıfır ise, δqj ‘ler bağımsız olduğu için, integralı sıfıra eşitlemenin tek yolu integrand’ın sıfır olması yani bağımsız genelleştirilmiş koordinat δqj'lerin katsayılarının sıfır olmasıdır. Burada, yukarıdaki figürde bahsedilen durağan etkiler altında, çok küçük değişimler sonucu alınan kırmızı yolun etkileri incelendiği için her durumda konfigurasyon değişimi sıfıra yakın olur (sanal yer değiştirme, diferansiyel yer değiştirme; δqj' çok küçük). Bu sonuçlardan, sistemin hareket denklemi ortaya konulabilir ve bu, Hamilton Prensibi ile şu şekilde özetlenebilir;
Bu duruma göre eğer sistem durağan etkiler altındaysa, Lagrangian’ın zamana göre toplamı sıfır olmaktadır. Eğer sistem üzerinde dinamik etkiler varsa, sistemin yukarıdaki hareket eğrisi kırmızıdan etkiye göre sapmakta ve mavi eğrilere gelmektedir. Bu durumda, Lagrangian’ın zaman göre integralı bize esasen dinamik etkileri verecektir. Dolayısıyla dinamik etkileri tanımlayan bir eylem ifadesini şu şekilde açıklayabiliriz;[32]
S, yani eylem; bir fonksiyoneldir (fonksiyonun fonksiyonu). Lagrangian fonksiyonunu t1den t2ye kadar alır ve skaler bir nicelik döndürür. Açısal momentum, [zaman].[enerji], [momentum].[uzunluk] gibi terimlerin birimiyle aynı birime sahiptir. Bu tanıma göre Hamilton’un minimum eylem prensibi sanal iş, sanal-difreansiyel yer değiştirme gibi nicelikler arasındaki ilişki şöyle özetlenebilir;
Dolayısıyla, Hamilton Prensibi ve Lagrangian yaklaşımı; Newton mekaniğindeki anlayışı tamamen değiştirmiş oluyor. (Metotlar doğru uygulandığında, sonuçların birebir aynı olduğu unutulmamalıdır.) Parçacıklar üzerindeki kuvvetlerin çıktısı olarak ivmeleri düşünmek yerine, modelimizi en az eyleme sahip olan yola ve eylemlerin o yolu nasıl değiştireceğine göre tanımlayabiliriz. Elbette burada eylem ve enerji fonksiyonlarını (Lagrangian) uygun tanımlamak ve genelleştirilmiş koordinatları veya değişkenleri doğru seçmek gerekmektedir. Parçacıkların konfigurasyon uzayında başlangıç ve bitiş anlık zamanları ile o zamanlara karşılık gelen noktaları tanımlayarak bu yolları ifade edebiliriz. Hamilton’un türettiği ilkeler bazen en az eylem ilkesi ile birebir tutulsa da, en az eylem ilkesinde hareket boyunca uygulanan eylemin durgun olması gerekmektedir. Hamilton prensipleri ile durgun olmayan dinamik eylemleri ve korunumsuz kuvvetleri de sistem modeline dahil etmemiz mümkündür ancak holonomik olmayan kısıtlarda çalışmamız yine mümkün değildir. Holonomik olmayan kısıtlar için ise D’Alambert’in sanal iş kavramından faydalanmamız gerekmektedir.
Lagrange çarpanları ve kısıtların ifade edilmesi[değiştir | kaynağı değiştir]
Lagrangian Lnin kartezyen rk koordinatlarında N parçacık için değişimini şu şekilde ifade edebiliriz;
Hamilton prensipleri, Lagrangian’daki genelleştirilmiş koordinatlar –sistemin davranışını tamamen tanımlıyor olması koşulu ile- bağımlı olsalar bile geçerlidir. Ancak kısıtların yine de holonomik olması gerekmektedir.[33] Bu açıdan Hamilton prensipleri durum uzayı ifadeleri ile benzerlik gösterir.
Eğer seçilen genelleştirilmiş koordinatlar rkler bağımsız değil ise sanal işte ve yer değiştirmede yaptığımız gibi δrknin katsayılarını sıfıra eşitlememiz mümkün değildir. Çünkü artık bağımsız yer değiştirmelerin sıfır olmayacağından emin olsak bile bağlıların sıfır olma veya onları oluşturacak kuvvetlerin olmaması ya da olması gibi bilinmezlikler ortaya çıkmaktadır. Bu sorunu, Lagrange çarpanları metodunu kısıtları ifade edecek şekilde kullanarak çözebiliriz. Her kısıt denklemi fi(rk, t) = 0yı bir Lagrange çarpanı λi for i = 1, 2, ...,C ile çarpabiliriz. Ve bu ifadeleri orijinal Lagrangian ifadeleri ile birleştirdiğimizde artık yeni bir Lagrangian tanımlamış oluruz;
Bunu, bağımlı olarak tanımlanmış koordinatları bağımsız koordinatlara çevirmek yerine onları tanımlayan fonksiyonu değiştirmişiz gibi düşünebiliriz. Böylece, özellikle komplike sistemlerdeki bağımsız koordinat seçimi probleminden kurtularak; hesaplamaya daha uygun bir metodoloji ortaya konmuş olur.
Lagrange çarpanları zamanın herhangi birer fonksiyonudur, ancak genelleştirilmiş rk koordinatlarının fonksiyonu değillerdir. Dolayısıyla karmaşık fonksiyonlar oluşturmazlar(Çarpanlar, pozisyon koordinatları ile eşit düzeyde ifade bulmaktadırlar). Bu yeni Lagrangian, sistematik olarak koordinatlarımızın bağımsızlığı ve kısıtların ayrı ifadesi (ki bu iki durum birbirine yakından bağlıdır) sorunlarına çözüm bulabilmektedir. Dolayısıyla, yeni Lagrangian’ı Euler-Lagrange denklemlerine koyarak;
İfadesini kısıt denklemleri olarak elde edebiliriz. Ayrıca rk cinsinden hareket denklemlerini Lagrange’in birinci tip denklemleriylede şu şekilde ifade edebiliriz;
Bu denklemlerde yeni Lagrangian’ın yukarıda bahsettiğimiz değişimini zaman göre integre edersek;
ifadesini buluruz ve temel aldığımız prensiplerden ötürü, uç noktaların ve ona bağlı anların sabit olduğunu her k için unutmamamız gerekir. (δrk(t1) = δrk(t2) = 0) Çarpanlar, daha önceki metotlarda olduğu gibi δrkların katsayılarını sıfırlayacak şekilde seçilirse, karşılaştığımız çarpan problem sorunu çözülür ve kısıtlar ile bağlılık problemini içsel bir şekilde ifade etmiş oluruz. Böylece bağımsız olmayan genelleştirilmiş koordinatlar için uygun çarpanlarla (kısıtları ifade eden çarpanlar) hareket denklemini bulabiliriz.
Eğer bir korunumlu kuvvetin gradyanı sisteme bir potansiyel enerji V bazında etkiyorsa, ve bu V sadece rkların birer fonksiyonu ise Lagrangian L = T − Vnin denklemlere konulması ile;
elde edilir. Newton’un 2. Yasasının bu Lagrangian formunda, kinetik enerjinin türevi(negatif olarak denklemde yer bulmakta); k parçacığına etkiyen toplam kuvvete; potansiyel enerjilerin türevi de kısıtlayıcı olmayan kuvvetlere karşılık gelmektedir. Yani;
Ve bunu yukarıdaki temel denkleme koyduğumuzda, kısıtlayıcı kuvvetleri şöyle buluruz;
ve en temel denklemimize dönersek; birinci terim (pozisyona göre türevlenmiş) momentumun türevini ifade ederken diğer terimler ise kuvvetleri ifade eder ve sistemi çözmemizi sağlar. Burada hem kısıtlayıcı (ve belki sistemimizden boş yere enerji çekecek) kuvvetleri hem de diğer kuvvetleri ayrı olarak bulmamız da önemlidir. Bu sayede sistem optimizasyonu da yapılabilir.
Lagrange-Euler denklemlerinin özellikleri[değiştir | kaynağı değiştir]
Bazı durumlarda; Lagrangian, hareket denklemlerini çözmeye gerek kalmadan bize sistem hakkında bilgi verebilir. Bunu Lagrange’in ikinci tip denklemleri sağlar.
Çözümlerin tekilliği[değiştir | kaynağı değiştir]
Bir sistem için Lagrangian fonksiyonu tekil değildir. Zira, sistemlerin özelliklerine göre de Lagrangian fonksiyonu farklı şekillerde tanımlanmalıdır. Lagrangian L sıfır olmayan bir çarpan a ile çarpılabilir ve rastgele bir b sabiti ile toplanabilir. Dolayısıyla yeni Lagrangian aL + b olacaktır ve bu fonksiyon, L ile aynı hareket tanımını gerçekleştirmektedir. Aynı zamanda Lagrangian, genelleştirilmiş koordinatlardan oluşan fonksiyonların kısmi olmayan, normal türevlerinden de etkilenmez.[34]
Burada L′ ve L tamamen aynı hareketi tanımlarlar.[35][36]
Noktasal değişimlerden bağımsızlık[değiştir | kaynağı değiştir]
Lagrangian’ın tanımlandığı genelleştirilmiş koordinat setini yani qyu başka bir genelleştirilmiş koordinat seti se çevirmek için kullanılacak nokta değişimi q = q(s, t) uygulanırsa yeni Lagrangian L′ (yeni koordinat setinin bir fonksiyonu);
şeklinde ifade edilir. Ayrıca, zincir kuralı kısmi diferansiyellere uygulanırsa, Lagrange denklemlerinin bu tip bir noktasal dönüşüm altında değişmez olduğu görülür;[37]
Bu sayede birçok denklem daha basit çalışabileceğimiz koordinat sistemlerine dönüştürülerek; hesaplama süresi azaltılabilir. Bu prosedür, Hamilton mekaniğindeki kanonik dönüşümler ile aynı mantığı içerir. Hamilton fonksiyonları da benzer şekilde, kanonik dönüşümlerden etkilenmezler.
Devrî koordinatlar ve korunum yasaları[değiştir | kaynağı değiştir]
Lagrangian’ın başka bir önemli özelliği ise, tanımladığı sistem içinde; dinamik davranış boyunca korunan özellikleri ifade etmesidir. Örneğin genelleştirilmiş momentum, kanonik olarak genelleştirilmiş koordinat qia eşleniktir ve şu şekilde tanımlanır;
Eğer, Lagrangian L qia bağlı değilse Euler-Lagrange denklemleri bize genelleştirilmiş momentumun korunan bir değer olduğunu söyler. Çünkü zamana bağlı türevi sıfırdır. Hareket de zamanın değişimiyle gerçekleştiğine göre momentumun hareket boyunca sabit kalması gerektiği sonucuna ulaşırız;
Bu, Noether teoreminin özel bir halidir. Bu tip koordinatlar devrî veya ihmal edilebilir koordinatlar olarak tanımlanır. Örneğin sistem şeklinde bir Lagrangian’a sahip olabilir. r ve z burada doğru boyuncaki uzunluklar, s eğrisel uzunluk, θ ve φ ise açılardır. Lagrangian’da z,s ve φnin bulunmadığına dikkat etmek gerekir. Ancak bu konumların hızları bulunmaktadır. Bu nedenle momentum değerleri;
olarak bulunur ve bunların hepsi korunan değerlerdir. Bu genelleştirilmiş momentumların birimleri tanımlandıkları koordinatlara bağlıdır. Örneğin pz yönündeki doğrusal hareket momentumu, psde s boyuncaki doğrusal momentum, pφ ise ölçüldüğü düzlemdeki açısal momentumu ifade eder. Ancak karmaşık hareketlere sahip olan sistemlerde bu korunumlar hareketi kompleksleştirir.
Enerji korunumu[değiştir | kaynağı değiştir]
Lagrangian’ın zamana göre toplam diferansiyeli alındığında çok genel bir sonuç elde ederiz;
Eğer bütün Lagrangian zamandan harici olarak bağımsız ise, Lagrangian’ın zamana göre kısmî türevi sıfırdır.(∂L/∂t = 0) Dolayısıyla parantez içindeki terimi şöyle tanımlayabiliriz;
Bu terim, bütün hareket boyunca sabit kalmalıdır. Buradan da kinetik enerjinin genelleştirilmiş koordinatlara bağlı ikinci dereceden homojen fonksiyon olduğu sonucuna varabiliriz. Ayrıca, ek olarak potansiyel V de sadece genelleştirilmiş koordinatların birer fonksiyonu olup hızlardan bağımsız ise, direkt hesaplamayla veya Euler’in homojen fonksiyonlar için geliştirdiği teoremler ile;
sonucuna varılır.[38] Bu durumlar altında, E sabiti şöyle tanımlanabilir;
Bu ise sistemin toplam korunan enerjisine karşılık gerekebilir. Sistem değiştikçe ve dinamik davranış gösterdikçe kinetik ve potansiyel enerjiler değişebilir ancak sistemin hareketi üzerindeki kısıt; toplam enerjisinin sıfır olmasıdır. Bu özellik hesaplamaları oldukça kolaylaştırmaktadır çünkü enerji yani E sanki sabit bir integrasyondaki herhangi bir sabitmiş gibi davranır. Ayrıca bu durumda, enerji ilişkilerinden hızların da integralini almak mümkündür. Ve bu, koordinatlar için yapılacak çözümlere kolaylık sağlar. İki durumda da (kinetik enerji veya hız) zamana bağlı olabilir; bu durumda simetri bozulur ve enerji korunmaz. Burada dikkat edilmesi gereken başka bir konu ise, Hamiltonian’ın Lagrangian ile Legendre dönüşümüne bağlı olan ilişkisinden bu sonuç yine türetilebilir;
Aynı durumlar geçerli ise, Hamilton fonksiyonu sistemin korunan toplam enerjisine eşittir.
Mekanik benzerlik[değiştir | kaynağı değiştir]
Eğer potansiyel enerji, genelleştirilmiş koordinatların zamandan bağımsız homojen fonksiyonu ise[39] ve her pozisyon vektörü sıfır olmayan bir sabit ile büyütülürse, yani;
Ve zaman; bir beta faktörü ile büyütülürse, t′ = βt, bu durumda hızlar vkda α/β faktörü ile büyümüş olur(kinetik enerji de bunun karesi kadar). Tüm Lagrangian aslında aynı faktör ile büyütülür;
Uzunluklar ve zaman büyütüldüğü için, sistem parçacıklarının islediği yollar geometrik olarak benzer ama büyüklük olarak farklıdır. t zamanda alınmış l uzunluğu eğer orijinal yol ise, bu dönüşümlerle artık yeni bir l′ olacak, zaman ise t′ olacaktır ve bunlar şu şekilde tanımlanır;
İlişkili parçacıklar[değiştir | kaynağı değiştir]
Verilen bir sistem için iki alt sistem A ve B eğer ilişkili değilse sistemin toplam Lagrangian’ı;A and LB for the subsystems:[34]
olarak ifade edilir. Ancak parçacıklar ilişkiliyse bu mümkün değildir. Bazı durumlarda sistemin toplam Lagrangian’ını alt parçaların Lagrangian’ları ile ifade etmek çok işe yarar. Bazı daha genel sistemlerde ise ilişkinin olmadığı Lagrangianlar ile ilişki hakkında bilgi taşıyan başka bir Lagrangian LAB ile toplayarak sistemi modellemek mümkündür.
Özellikle mekanik ilişkilerin bulunduğu sistemlerde bu doğrusal özellik çok kullanışlıdır. Bu uygulama, fiziksel olarak da etkileşim göstermeyen Lagrangian’ların kinetik enerjiyle ilişkili; etkileşim içinde olanların ise potansiyel enerjiye karşılık geleceği gibi gerçeklenebilir. Önemsenmeyen etkileşimler için Lab sıfır alınabilir. Burada, potansiyel enerjinin daha önceki denklemlerde, sistemlerin koordinatlar boyunca nasıl kısıtlandıkları hakkında bilgi verirken kinetik enerjinin hareket hakkında bilgi verdiği konusu da tekrarlanmış oluyor. Elbette, iki parçacıklı bir sistem için tanımlanan bu yöntem, çok parçacıklı sistemlere genelleştirilebilir. Bu durumda her parçacık arası ilişkilerin ifade edilmesi gerekir.
Lagrange mekaniğinin başka konulardaki uygulamaları[değiştir | kaynağı değiştir]
Hamiltonian, Lagrangian’a Legendre dönüşümü uygulanarak bulunur. Dolayısıyla, orijinal değişkenler ile kanonik olarak eşlenik yeni değişkenler elde edilmiş olur. Dolayısıyla Hamilton mekaniğinde değişken sayısı ve diferansiyel denklem sayısı iki katına çıkar ancak dereceler bire indirgenir. Bu, durum uzayı ifadeleri ile de esasen oldukça paraleldir. Hamilton fonksiyonu aynı Lagrangian fonksiyonunun Lagrange denklemleriyle olan ilişkisi gibi Hamilton mekaniğinin temelidir. Klasik görüşe göre zaman bağımsız bir değişkendir ve hız ile pozisyon zamana bağlıdır. Bu değişkenler ise genelde durum-faz uzayında incelenir ve çevrimler, dengeler ve stabilite bu şekilde incelenir.
Routhian mekaniği; Lagrange ve Hamilton mekaniklerinin bir hibrit formülasyonudur. Ancak çevrimsel koordinatlar haricinde hesaplama açısından pek etkili değildir.
Mühendislikteki kullanımları[değiştir | kaynağı değiştir]
Circa 1963'te Lagrangian fonksiyonlarının mühendislikte kullanımını önermiş ancak birkaç yıl sonra, dinamik sistemlerdeki üstünlüklerine rağmen mühendislik müfredatlarından çıkarılarak teorik dinamik alanına kaydırılmıştır. Zira, Lagrangian sadece makina mühendisliğinde değil, Elektrik Elektronik Mühendisliği; finans, ekonomi, biyoloji ve birçok diferansiyel değişimin olduğu alanda kendine yer bulmuştur. Zira bu alanlarda birçok yol-integral ifadeleri ve parabolik kısmî diferansiyel denklemler bulunmaktadır.
Lagrangian fonksiyonları birçok mühendislik problemine hızlı, yazılıma uygun ve rahat çözümler sunmaktadır. Ayrıca, normal mekanikle formülasyonu bile çok zor olan sistemleri hem felsefi olarak hem de dinamik olarak daha rahat formüle etmemizi sağlar. Robotik, akışkanlar mekaniğinde akış modelleri, (Akışın Euler ve Lagrange spesifikasyonları), sinyal işleme, nanoteknoloji, süper bilgisayarlar, kimya mühendisliği, inşaat mühendisliği gibi alanlarda kendine yer bulur. Lagrangian gibi enerji fonksiyonları özellikle akış kavramının etkin olduğu diferansiyel denklemlerde kendine yer bulur. Özellikle doğrusal olmayan sistemlerde akış konsepti önemlidir ve bunları çözmek için geliştirilen Lyapunov fonksiyonları da enerji temellidir.
Ayrıca bakınız[değiştir | kaynağı değiştir]
Notlar[değiştir | kaynağı değiştir]
- ^ a b Dvorak & Freistetter 2005, s. 24
- ^ Haken 2006, s. 61
- ^ Lanczos 1986, s. 4
- ^ Menzel & Zatzkis 1960, s. 160
- ^ Feynman
- ^ Goldstien, Poole & Safko 2001, s. 35
- ^ "Arşivlenmiş kopya" (PDF). 4 Mart 2016 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 5 Ocak 2016.
- ^ Hand & Finch 2008, s. 36–40
- ^ Torby1984, p.270
- ^ a b Torby 1984, s. 269
- ^ Hand & Finch 2008, s. 60–61
- ^ {harvnb|Hand|Finch|2008|page=19}}
- ^ Penrose 2007
- ^ Schuam 1988, s. 156
- ^ Synge & Schild 1949, s. 150–152
- ^ a b Hand & Finch 2008, s. 44–45
- ^ Foster & Nightingale 1995, s. 89
- ^ Hand & Finch 2008, s. 4
- ^ Goldstein 1980, s. 16–18
- ^ Hand 2008, s. 15
- ^ Hand & Finch 2008, s. 15
- ^ Fetter & Walecka 1980, s. 53
- ^ Torby 1984, s. 264
- ^ Torby 1984, s. 269
- ^ Kibble & Berkshire 2004, s. 234
- ^ Fetter & Walecka 1980, s. 56
- ^ Hand & Finch 2008, s. 17
- ^ Hand & Finch 2008, s. 15–17
- ^ R. Penrose (2007). The Road to Reality. Vintage books. s. 474. ISBN 0-679-77631-1.
- ^ Goldstien 1980, s. 23
- ^ Kibble & Berkshire 2004, s. 234–235
- ^ Hand & Finch 2008, s. 51
- ^ Fetter & Walecka, ss. 68–70
- ^ a b Landau & Lifshitz 1976, s. 4
- ^ Goldstien, Poole & Safko 2002, s. 21
- ^ Landau & Lifshitz 1976, s. 4
- ^ Goldstein 1980, s. 21
- ^ Landau & Lifshitz 1976, s. 14
- ^ Landau & Lifshitz 1976, s. 22
Kaynakça[değiştir | kaynağı değiştir]
- Penrose, Roger (2007). The Road to Reality. Vintage books. ISBN 0-679-77631-1.
- Landau, L. D.; Lifshitz, E. M. Mechanics (3.3sayfa=134 bas.). Butterworth Heinemann. ISBN 9780750628969.
- Landau, Lev; Lifshitz, Evgeny (1975). The Classical Theory of Fields. Elsevier Ltd. ISBN 978-0-7506-2768-9.
- Hand, L. N.; Finch, J. D. Analytical Mechanics (2.2sayfa=23 bas.). Cambridge University Press. ISBN 9780521575720.
- Louis N. Hand, Janet D. Finch (1998). Analytical mechanics. Cambridge University Press. ss. 140-141. ISBN 0-521-57572-9. 24 Şubat 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 6 Ocak 2016.
- Kibble, T. W. B.; Berkshire, F. H. Classical Mechanics (5.5yıl=2004 bas.). Imperial College Press. ss. 236. ISBN 9781860944352.
- Goldstein, Herbert. Classical Mechanics (2.2yıl=1980 bas.). San Francisco, CA: Addison Wesley. ss. 352-353. ISBN 0201029189.
- Goldstein, Herbert; Poole, Charles P., Jr.; Safko, John L. Classical Mechanics (3.3yıl=2002 bas.). San Francisco, CA: Addison Wesley. ss. 347-349. ISBN 0-201-65702-3. 15 Ocak 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 6 Ocak 2016.
- Lanczos, Cornelius (1986). "II §5 Auxiliary conditions: the Lagrangian λ-method". The variational principles of mechanics (Reprint of University of Toronto 1970 4th bas.). Courier Dover. s. 43. ISBN 0-486-65067-7. 27 Haziran 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 6 Ocak 2016.
- Fetter, A. L.; Walecka, J. D. (1980). Theoretical Mechanics of Particles and Continua. Dover. ss. 53-57. ISBN 978-0-486-43261-8.
- The Principle of Least Action, R. Feynman
- Dvorak, R.; Freistetter, Florian (2005). "§ 3.2 Lagrange equations of the first kind". Chaos and stability in planetary systems. Birkhäuser. s. 24. ISBN 3-540-28208-4. 27 Haziran 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 6 Ocak 2016.
- Haken, H (2006). Information and self-organization (3.3yayıncı=Springer bas.). s. 61. ISBN 3-540-33021-6. 27 Haziran 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 6 Ocak 2016.
- Henry Zatzkis (1960). "§1.4 Lagrange equations of the second kind". DH Menzel (Ed.). Fundamental formulas of physics. 1 (2.2erişimtarihi=6 Ocak 2016 bas.). Courier Dover. s. 160. ISBN 0-486-60595-7. 27 Haziran 2014 tarihinde kaynağından arşivlendi.
- Francis Begnaud Hildebrand (1992). Methods of applied mathematics (Reprint of Prentice-Hall 1965 2nd bas.). Courier Dover. s. 156. ISBN 0-486-67002-3. 24 Şubat 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 6 Ocak 2016.
- Michail Zak, Joseph P. Zbilut, Ronald E. Meyers (1997). From instability to intelligence. Springer. s. 202. ISBN 3-540-63055-4. 24 Şubat 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 6 Ocak 2016.
- Ahmed A. Shabana (2008). Computational continuum mechanics. Cambridge University Press. ss. 118-119. ISBN 0-521-88569-8.
- John Robert Taylor (2005). Classical mechanics. University Science Books. s. 297. ISBN 1-891389-22-X. 24 Şubat 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 6 Ocak 2016.
- Padmanabhan, Thanu (2000). "§2.3.2 Motion in a rotating frame". Theoretical Astrophysics: Astrophysical processes (3.3yayıncı=Cambridge University Press bas.). s. 48. ISBN 0-521-56632-0.
- Doughty, Noel A. (1990). Lagrangian Interaction. Addison-Wesley Publishers Ltd. ISBN 0-201-41625-5.
- Kosyakov, B. P. (2007). Introduction to the classical theory of particles and fields. Berlin, Germany: Springer. doi:10.1007/978-3-540-40934-2.
- Galley, Chad R. (2013). "Classical Mechanics of Nonconservative Systems". Physical Review Letters. 110 (17). s. 174301. arXiv:1210.2745 $2. Bibcode:2013PhRvL.110q4301G. doi:10.1103/PhysRevLett.110.174301. PMID 23679733.
- Birnholtz, Ofek; Hadar, Shahar; Kol, Barak (2014). "Radiation reaction at the level of the action". International Journal of Modern Physics A. 29 (24). s. 1450132. arXiv:1402.2610 $2. Bibcode:2014IJMPA..2950132B. doi:10.1142/S0217751X14501322.
- Birnholtz, Ofek; Hadar, Shahar; Kol, Barak (2013). "Theory of post-Newtonian radiation and reaction". Physical Review D. 88 (10). s. 104037. arXiv:1305.6930 $2. Bibcode:2013PhRvD..88j4037B. doi:10.1103/PhysRevD.88.104037.
- Roger F Gans (2013). Engineering Dynamics: From the Lagrangian to Simulation. New York: Springer. ISBN 978-1-4614-3929-5. 24 Şubat 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 6 Ocak 2016.
- Terry Gannon (2006). Moonshine beyond the monster: the bridge connecting algebra, modular forms and physics. Cambridge University Press. s. 267. ISBN 0-521-83531-3. 24 Şubat 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 6 Ocak 2016.
- Torby, Bruce (1984). "Energy Methods". Advanced Dynamics for Engineers. HRW Series in Mechanical Engineering. United States of America: CBS College Publishing. ISBN 0-03-063366-4.
- Foster, J; Nightingale, J.D. (1995). (2.2başlık=A Short Course in General Relativity bas.). Springer. ISBN 0-03-063366-4. Eksik ya da boş
|başlık=(yardım) - M. P. Hobson, G. P. Efstathiou, A. N. Lasenby (2006). General Relativity: An Introduction for Physicists. Cambridge University Press. s. 79–80. ISBN 9780521829519. 7 Mart 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 6 Ocak 2016.
Konuyla ilgili yayınlar[değiştir | kaynağı değiştir]
- Gupta, Kiran Chandra, Classical mechanics of particles and rigid bodies (Wiley, 1988).
- Cassel, Kevin W.: Variational Methods with Applications in Science and Engineering, Cambridge University Press, 2013.































![{\displaystyle \sum _{j=1}^{n}\left[Q_{j}-\left({\frac {d}{dt}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}\right)\right]\delta q_{j}=0\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73844b508fd1c52d362da50afaf12acc18f8b045)




![{\displaystyle \int _{t_{1}}^{t_{2}}\delta L\,dt=\sum _{j=1}^{n}\left[{\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j}\right]_{t_{1}}^{t_{2}}+\int _{t_{1}}^{t_{2}}\sum _{j=1}^{n}\left({\frac {\partial L}{\partial q_{j}}}-{\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)\delta q_{j}\,dt\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02625030b0d118b7d3d7bb9e1b0d943f274ffddf)



























