Klasik mekanik
| Klâsik mekanik |
|---|
Klasik mekanik, makroskobik boyutlarda (~10−9 m >) cisimlerin hareketlerini hem deneysel hem de matematiksel olarak inceleyen, fiziğin iki ana dalından biridir.
Klasik mekanik basit kristal modellerinden, galaksilerin hareketlerine kadar oldukça geniş bir büyüklük skalasında tutarlı sonuçlar vermektedir. Bunların yanı sıra, çevremizde gördüğümüz birçok mekanik olay klasik mekanik kullanılarak oldukça yüksek bir doğrulukla hesaplanabilir.
Klasik mekanik, Newton mekaniği, klasik istatistik mekanik ve klasik elektromanyetik teori alt dallarını içinde barındırır. Özel ve genel görelilik kuramları bazı kaynaklarca klasik mekaniğin bir alt dalı olarak kabul edilse de bu kuramların yapıları gereği klasik mekaniğin veya kuantum mekaniğinin bir alt dalı olmak yerine bu kuramları, ışık hızına yakın hızlarda veya kütleçekimin büyük olduğu durumlarda modifiye ettiğini söylemek daha doğru olur.
Klasik mekanik günlük olaylar çerçevesinde oldukça kesin sonuçlar üretmektedir, ancak ışık hızına yakın hızlarda hareket eden sistemler için göreli mekanik (relativistic mechanics), çok küçük uzaklık ölçeklerinde sistemler için nicemleme mekaniği (quantum mechanics) ve her iki özelliğe sahip sistemler için de göreli nicemleme alan teorisi (relativistic quantum field theory) kullanılmalıdır. Klasik mekaniğin araştırma dalları için yandaki şablonu kullanabilirsiniz.
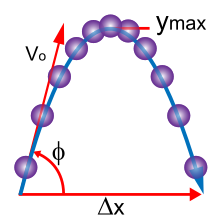
Konum ve türevleri[değiştir | kaynağı değiştir]
| Mekaniğin birimleri | |
| Konum | m |
| Açı | birimsiz (radyan) |
| Hız | m s−1 |
| Açısal hız | s−1 |
| İvme | m s−2 |
| Açısal ivme | s−2 |
| Sarsım (fizik) | m s−3 |
| Eylemsizlik momenti | kg m2 |
| Momentum | kg m s−1 |
| Açısal momentum | kg m2 s−1 |
| Kuvvet | kg m s−2 |
| Tork | kg m2 s−2 |
| Enerji | kg m2 s−2 |
| Güç | kg m2 s−3 |
| Basınç ve Enerji yoğunluğu | kg m−1 s−2 |
| Yüzey gerilimi | kg s−2 |
| Yay sabiti | kg s−2 |
| Kinematik akmazlık | m2 s−1 |
| Dinamik akmazlık | kg m−1 s−1 |
| Yoğunluk | kg m−3 |
| Aksiyon | kg m2 s−1 |
Noktasal bir parçacığın konumu uzayda rastgele seçilen O referans noktasından, parçacığa çizilen vektördür.
Hız ve sürat[değiştir | kaynağı değiştir]
Hız ya da yerdeğiştirmenin zamana oranı, konumun zamana göre birinci türevi olarak tanımlanır.
- .
İvme[değiştir | kaynağı değiştir]
İvme ya da hızın zamana oranı, hızın zamana göre türevi (aynı zamanda konumun ikinci türevi) olarak tanımlanır.
Sınırları[değiştir | kaynağı değiştir]

Klasik mekaniğin birçok dalı genel göreliliğin ve göreli istatistiksel mekaniğin basitleştirilmiş ve günlük yaşama uyarlanmış halidir.
Newton kanunlarının genel hali[değiştir | kaynağı değiştir]
Özel görelilikte, bir parçacığın momentumu şudur:
m parçacığın kütlesi, v hızı ve c ışık hızı
Eğer v c ye göre çok küçükse kökün içi yaklaşık 1 olur ve
Böylece klasik mekaniğin p=mv eşitliğinin aslında ışık hızına göre çok daha küçük hızlarda hareket eden cisimler için basitleştirilmiş bir eşitlik olduğu görülebilir.
Dalları[değiştir | kaynağı değiştir]
Klasik mekanik, ilk önce geleneksel üç ana dala ayrıldı:[1]
- Statik, kuvvetlerin ve momentlerin etkisi altında cisimlerin denge durumlarını inceler.[1]
- Dinamik, hareket ve kuvvet arasındaki ilişkiyi inceler.[1]
- Kinematik, kuvvetleri hesaba katmadan hareketlerin etkileri ile uğraşır.[1]
Bütün mekaniksel büyüklükler kütle (kilogram), uzunluk (metre) ve zaman (saniye) cinsinden ifade edilebilmektedir.
Ayrıca bakınız[değiştir | kaynağı değiştir]
- Atwood düzeneği
- Mekanik
- Newton'un hareket kanunları
- Newton'un evrensel çekim kanunu
- Kuantum mekaniği
- Özel görelilik kuramı
Kaynakça[değiştir | kaynağı değiştir]
Dış bağlantılar[değiştir | kaynağı değiştir]
- Klasik mekanik[ölü/kırık bağlantı]
- http://www.fizikevreni.com4 Mart 2009 tarihinde Wayback Machine sitesinde arşivlendi.
- http://www.fizikevreni.com/klasikmekanik1.pdf24 Ağustos 2009 tarihinde Wayback Machine sitesinde arşivlendi.
- http://www.fizikevreni.com/klasikmekanik2.pdf23 Eylül 2010 tarihinde Wayback Machine sitesinde arşivlendi.
| Wikimedia Commons'ta Klasik mekanik ile ilgili ortam dosyaları bulunmaktadır. |





