Açısal hız
Açısal hız, bir objenin birim zamandaki açısal olarak yer değiştirme miktarına verilen isimdir. Açısal hız vektörel olup bir cismin bir eksen üzerindeki dönüş yönünü ve hızını verir. Açısal hızın SI birimi radyan/saniyedir, ancak başka birimlerde de ölçülebilir (açı/saniye, açı/saat vb.). Açısal hız genellikle omega sembolü (ω, bazen Ω) ile gösterilir. Açısal hızın yönü genellikle dönüş düzlemine diktir ve sağ el kuralı ile bulunabilir.
Bir parçacığın açısal hızı[değiştir | kaynağı değiştir]
Bir parçacığın açısal hızı belirlenen bir merkez noktaya göre hesaplanır. Resimde görüldüğü gibi (ɸ ve θ açıları) ve merkez (O) dan (P) noktasına bir çizgi çekilir. Bu işlem sonrasında (v) cismin hızının düzlem üzerinde bileşenleri ortaya çıkar. Eğer karşı bir bileşen yoksa cisim bir çember şeklinde dönmeye başlar.

Eğer dikey bir saptırıcı bileşen yoksa, cisim merkezden düz bir çizgi yolunda ilerler.

Yarıçapa bağlı bir hareket parçacığın hareket yönünde herhangi bir değişime yol açmaz bu sebeple açısal hız bulunurken yarıçap yönündeki hareketi hesabımıza katmamıza gerek yoktur. Açısal hızın oluşması bu durumda tamamen dik olan hareketlerden oluşur. İki boyutlu işlemlerde açısal hız (ω): işlemi ile bulunur. İki boyutlu harekette harekete dik olan hız bileşenleri kullanılır:. Bu formüldeki hız ve açı için daha açık formülümüz: . Bu iki formülün birleşimi ise bizlere açısal hızı verir:
İki boyutlu durumlarda açısal hız tek bir sayı olarak sonuçlanır ve yönü yoktur ancak bir eksen yönü vardır. İki boyutlu hareketlerde açısal hızın işareti bulunduğu eksenin değişmesi ile değişir. Bu değişime eksenlerin yerlerinin değiştirilmesi de eklenebilir, tıpkı x ekseni ve y eksenlerinin değiştirilmesi gibi. Eğer eksenler yer değiştirilmez ve sadece yönler değişirse açısal hızın sadece işareti değişir. Bir elips yörüngesinde ilerleyen üç tür açısal hız mevcuttur: Doğru açısal hız, merkezsiz açısal hız ve ortalama açısal hız.
Üç boyutta parçacık[değiştir | kaynağı değiştir]
Üç boyutta, açısal hız biraz daha karışık bir hal almaktadır. Bu durumlarda açısal hız bir vektör olarak kabul edilir ve artık bir büyüklüğünün yanında ayrıca bir yönü vardır. Büyüklük açısal sürati ifade ederken, yön ise dönüş eksenini gösterir. Sağ el kuralı açısal hızın pozitif olduğu yönü gösterir. sembolünü anlık dönüş eksenine bağlı vektör olarak kabul edersek, vektörün üzerinden bakıldığında dönüş saat yönünün tersine doğrudur. Bu durumda açısal hız vektörü şu şekilde ifade edilir:
Tıpkı iki boyutta parçacıkta olduğu gibi, parçacık yarıçap üzerinde bir hız vektörü bileşeni olmasını ister ve ayrıca bir başka bileşende bu yarıçapa dik olmalıdır. Merkez noktasındaki bileşenin ve dik olan bileşenin birleşmesi sonucu bir dönüş yüzeyi meydana gelir ve bu yüzeyde parçacığın hareketi tıpkı iki boyutlu hareketteki gibidir. Bu durumda dönüş ekseni düz bir çizgi halini alır ve bu eksen açısal hızın yönü olarak belirlenir. Birim vektör kullanılarak açısal hız formülü (iki boyut için) şöyle yazılabilir: ve vektör çarpımı ile şu şekilde düzenlenebilir:
Eğer bir nokta ile ye göre döner ise, diğer bir noktada ile e göre dönerse bu iki noktanın açısal hızını e göre ile gösterebiliriz. Açısal hız bu şekilde tanımlandığı zaman bir gerçek vektör haline gelir çünkü iki eklenimi vardır:
- İçeri bir yükleme ki bu yükleme; ilişkisel, değiştirilebilen, dağıtılabilen ve sıfır birim elemanı içerir
- Dışarıdan yükleme ise, dış noktanın normal özelliklerine bağlıdır.
Bu eklenimler vektör boşluğunun tanımıdır. Formül olarak yazılırken en çok zorlanılan birim değiştirilebilen eklenimdir. Eğer dönüş matrisi olursa zamanda sonsuz dönümün türevidir. Bu sebepten dolayı; ile ifade edilebilir. Genellikle dönüşler değiştirilebilir değildir ancak sonsuz dönüş eklendiği zaman formülümüz; ve alınabilir.
Noktalara göre dönüş[değiştir | kaynağı değiştir]
Belirli bir noktaya göre oluşan dönüşün üç vektörünün, herhangi bir zaman aralığındaki açısal hızları eşit olmalıdır. Bu tür noktalardaki her vektör bir önceki konudaki (hareket eden parçacık) gibi sabit değeri olan vektörlerdir. Bu konu hareket eden parçacığın dönüşüne benzese de, esnemez-katı cisimlerle yakından bağlantılı olduğu için daha önemlidir ve ölçümler için özel araç ve gereçler üretilmiştir. Bir noktaya bağlı dönüşün açısal hızı bulmanın iki yolu vardır bunlar; açısal hız vektörü ve açısal hız gergisidir. Bu iki birim birbirleri ile bağlantılıdır ve birbirlerini bulmada kullanılabilirler.
Bir noktaya göre açısal hız[değiştir | kaynağı değiştir]
Bir noktaya göre açısal hızın tanımı genel tanımla aynıdır ve bir farklılık göstermez. Euler teoremine göre bir noktaya bağlı oluşan bir dönüşün anlık bir dönüş ekseni vardır ve bu eksen herhangi bir zamanda incelendiğinde bulunmalıdır. Bir noktaya bağlı dönüşte açısal hız dönüş ekseni üzerinde yer alır. Eksene dik olan enine herhangi bir düzlemin iki boyutlu dönüş yapması gerekir. Bu sebeple herhangi bir T anındaki açısal hızın büyüklüğü iki boyutlu dönüşle tutarlı olmalıdır. Açısal hız toplam uygulaması ile tanımlanabilen bir vektördür. Birimleri birbirlerinin türevleri alınarak bir noktaya göre hareketin bulunmasını sağlar. (Euler açıları ya da dönüş matrisi)
Bir noktaya açısal hız vektörü eklenimi[değiştir | kaynağı değiştir]
Genel yaklaşımda, açısal hız vektörlerine yapılan toplam uygulaması hareket bileşimi ile tanımlanabilir. Bir noktaya bağlı dönüşlerde areket bileşimini uygulamak genel tanıma kıyasla daha kolaydır çünkü yapılan işlemler sonucunda ortaya çıkan son matris her zaman dönüş matrisinin bir ürünüdür. Genel durumda toplam değiştirilebilir.

Bir noktaya bağlı olarak vektörlerin bileşenleri[değiştir | kaynağı değiştir]
Formüle gerekli eklemeler yapıldığında: Matrisin kolonlarının vektörün noktaya bağlı bileşenleri olduğu için bize bir noktaya bağlı açısal hızın değerini ve türevini bulmamızı sağlar . Euler açılarından bileşenler
Açısal hızın bileşenleri ilk olarak Leonhard Euler tarafından ve kendi yarattığı Euler açıları ile hesaplanmıştır ve orta bir noktaya göre temelleri bulunmuştur: •Bir eksen devinim eksenidir. •Merkez noktasından hareket eden düğüm noktaları nütasyon ekseni oluşturur. •Bir eksende gerçek dönüş eksendir.

Euler yaptığı araştırmalar ile açısal hızın birimlerinin üç eksen ile çarpının aralarındakş açıların türevine eşit olduğunu kanıtlamıştır. (Bu sonuçlar ayrıca ilk dönüşün temellerini üç birincil euler dönüşü olarak tanımlanmasını sağlar. Bu formülde tabanlar ortonormal değildir ve kullanımı zordur, ancak bu formül ile hız vektörü hareket noktasına göre değiştirilebilir ve bunun için formül tabanları ile oynamak yeterlidir. Örnek olarak tabanlardan biri değiştirildiğinde: bu formüldeki IJK birim vektördür ve hareket eden cisme göre değişir. Bu örnek z-x-z düzenlenmesinin Euler açıları için kullanılması ile bulunmuştur.
Sonsuz küçük dönülerinin matrislerinin bileşenleri[değiştir | kaynağı değiştir]
Açısal hız vektörlerinin bileşenleri eğer var ise sonsuz küçük dönüşlerden şu şekilde hesaplanabilir; •Her dönüş matrisin bir özdeğeri olduğu için (genellikle +1’dir) bize dönüş eksenini verir. •Temel değerleri sonsuz küçük değerden türetilmiştir.
Açısal hız gergisi[değiştir | kaynağı değiştir]
Dönüş matrislerinden giriş bölümü açıklanabilir. Herhangi bir vector bir eksen etrafında açısal hızı ile dönerken bu formül kullanılabilir; Bu formülde açısal hız gergisini açısal hız ile bağlantılı şekilde yazabiliriz; Bu formüldeki gergi W(t) bir çarpımı gibi davranır; Matristeki A(t), açısal hız gergisi W ile şu şekilde bulunabilir: Açısal hız noktaya bağlı dönüşteki üç vektöre de eşit olmalıdır, eğer bir A(t) matrisi varsa kolonlarını bu vektörlere eşit olmalıdır ve formula şu şekilde yazılabilir; bu sebeple aradığımız açısal hız gergisi;
Açısal hız vektör gergisinin özellikleri[değiştir | kaynağı değiştir]
Genellikle n-boyutlu uzaydaki açısal hız açısal yer değiştirme gergisinin türevine eşittir. Bu W gergisi n(n-1)/2 bağımsız bileşeni vardır ve bu bileşenler Lie Matematiğinin Lie dönüş gruplarında n-boyutlu iç çarpımında yer alır.
Üstel W[değiştir | kaynağı değiştir]
Üç boyutta, açısal hız bir değişken vektör olarak tanımlanabilir çünkü ikinci dereceden gergiler üç boyutta değişken vektörlere eşittir. bu formül bir türevse ldenklem olarak A(t)’ye göre yazılabilir; Eğer açısal hız sabitse W’de sabittir ve denklemin türevi alınabilir ve sonuç; bu formül Lie dönüş gruplarına bağlanabilir. Açısal hız vektörleri formula ile gösterilebilir ve bu formül formülünü onaylar. Öncelikle formülü kanıtlamak için R(t) için türev almamız gerekir () R(t) dönüş matrisidir; Eğer (AB)t = BtAt formülü kullanılırsa; Gergi bir matris olarak ifade edildiğinde;
Koordinatsız tanım[değiştir | kaynağı değiştir]
Herhangi bir anında hız gergisi pozisyon vektörü ve hız vektörü arasında düz bir çizgi haritası oluşturur. Bu formülde parametresini ihmal ettik, ayrıca ve üç boyutlu Öklit vektörlerinin elemanları olarak kabul ettik. Bu formüle göre düzlem haritası ve açısal hız arasındaki bağlantı şöyledir. W ortogonal değişimin türevi olduğu için; Bu formüle dış işlem matematiği uygulanırsa ve özel bir lineer oluşurturur; ve in çarpım sonucudur. Çift vektör alındığında L* of L sonuç; ile tanımlanır ve Hodge bileşenleri uygulandığında; Açısal hız: rastgele bir vektör olduğu için vektör çarpımlarının sonucu;
Vektör düzlemine göre açısal hız[değiştir | kaynağı değiştir]
Açısal hız gergisi haritalarında hızlar yer değiştirmelerin vektör düzlemidir. Detaylı incelendiğinde bu vektör düzlemleri Killing vektör düzlemidir ve bir element olan Lie algebra so(3) ün üç boyutlu dönüş gruplarına SO(3) e aittir. SO(3) teki element açısal hız vektörü olarak kabul edilebilir.
Esnemez katı cisim bileşenleri[değiştir | kaynağı değiştir]
Açısal sürat için yazılmış tüm formüller dönüş yapan katı bir cisim içinde geçerlidir. Bu bölümde dönüş yapan sabit cismin bir eksen üzerinde dönmediği kabul edilmiştir. Bu bölümde sabit cismin, rastgele seçilmiş V(t) ile hareket eden bir noktaya göre dönüş yaptığı düşünülmüştür.
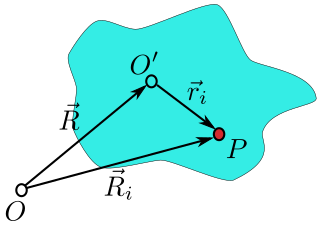
Denklemleri oluşturabilmek için katı cismin koordinat sisteminde bir noktaya göre sabit tutulduğu varsayılır, daha sonra bu koordinat düzlemi ve katı cisim arasındaki alan laboratuvar sisteminde incelenir. Resimde görüldüğü gibi laboratuvar sisteminin merkezi O noktasından O' noktasına kadar R’dir. Bir (i) parçacığı katı cisim üzerinde belirlenmiştir ve P noktası üzerinde olduğu kabul edilmiştir ve bu parçacığın vektör durumu Ri olarak alınmıştır (laboratuvar sistemi) ve (ri ) cisime göre alınmıştır. Parçacığın bulunduğu yer şe şekilde ifade edilebilir; Esnemez katı cisim için yapılan tanımlar bu cisim üzerindeki belirlenen noktalar arasındaki mesafenin zamanla değişmemesi kaydı ile doğru kabul edilir. Bu da uzunluğunun değişmemesi anlamına gelir. Euler dönüş teoremi kullanılarak nin yerine kullanılabilir ve 3x3 dönüş matrisidir. parçacığın herhangi bir zaman aralığındaki sabit noktadır t=0. Bu yerine yazma işlemi faydalıdır çünkü dönüş matrisi zamanla değişmektedir, sabittir. Bu sonuçla beraber dönüş matrisinin üç elemanı da dönüş yapan katı cismin bir parçası haline gelir ve dönüş eksenlerinde vektörler görülür hale gelir. Eğer dönüş ekseni vektörüne paralelse vektörü dönüş yapmaz. Sonuç olarak parçacığın yeri şu formülle açıklanır; eğer bu formülün türevi alınırsa bize parçacığın hızını verir: Vi parçacığın hızı (laboratuvar) ve V, O' noktasındaki hızdır (esnemez sabit cisme göre hız). dönüş matrisi olduğu için tersini bulmak istediğimizde; veya bir önceki açısal hız. Bu formüllerin kullanımından üç boyutlu vektörel düzlem oluşturulabilir. Önceki açısal hız vektörü Eğer w yi W yerine yazarsak bize matris yazılımı ve vektör çarpımı verir; Görüldüğü gibi katı bir cisim içerisindeki bir noktanın hızı iki birimde yazılabilir, katı cisim üzerinde belirlenmiş bir noktadaki hız artı açısal hız barındıran vektörel çarpım formülü. Bahsedilen açısal hız O' ve O arasındaki dönüş eksenindeki hızdır.
Tutarlılık[değiştir | kaynağı değiştir]
Esnemez katı cismin rastgele seçilmiş bir nokta etrafında dönüş yaptığını kabul ettik. Bir önceki konuda kanıtladığımız gibi açısal hızın merkeze göre seçilmesinin bir önemi olmadığını göstermiştik. Bu da bize açısal hızın dönüş yapan cismin kendine ait bir özellik olduğunu gösterir.

Laboratuvar sistemine göre merkez O noktasıdır ve O1 ile O2 cisim üzerinde sabit alınmış iki noktadır ve hızları ve dir. O1 ve O2 moktalarındaki açısal hızlar ve dir. Eğer bu şartlar sağlanırsa P noktası ve O2 tek bir hıza sahip olur; Bu iki formül bize yeni bir formül oluşturur; P noktası ve rasagele seçildiği için; Eğer seçtiğimiz nokta anlık dönüş ekseni üzerinde bir nokta olur ise, cisim üzerindeki bir noktanın hızı açısal hıza eşit olur. Bunun sebebi anlık dönüş eksenin hızının sıfır olmasıdır. Anlık dönüş eksenine örnek olarak kapı menteşesi verilebilir.
Kaynakça[değiştir | kaynağı değiştir]
• Symon, Keith (1971). Mechanics. Addison-Wesley, Reading, MA. ISBN 0-201-07392-7. • Landau, L.D.; Lifshitz, E.M. (1997). Mechanics. Butterworth-Heinemann. ISBN 0-7506-2896-0.








































































![{\displaystyle {\boldsymbol {\omega }}=[\omega _{x},\omega _{y},\omega _{z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8f418d52c41570663e22f7b19a8d3a427b69cab)









