Boole cebiri
Bu madde, Vikipedi biçem el kitabına uygun değildir. (Aralık 2017) |
Bu madde hiçbir kaynak içermemektedir. (Aralık 2017) (Bu şablonun nasıl ve ne zaman kaldırılması gerektiğini öğrenin) |
Boole cebiri değişkenlerin değerinin doğru ve yanlış olabildiği bir cebir altkoludur. Doğru ve yanlış değerleri genelde sırasıyla 1 ve 0 olarak ifade edilir. Değişken değerlerinin sayı, işlemlerin ise toplama ve çarpma olduğu temel cebrin aksine Boole cebrinde ∧ işareti ile ifade edilen "ve", ∨ işareti ile ifade edilen "veya", ¬ ile ifade edilen "değil" işlemleri bulunur.
Boole cebri ismini George Boole'den alır ve bu ismin ilk kez 1913 yılında Sheffer tarafından önerildiği iddia edilmektedir.
Sayısal devrelerin analiz ve tasarımı boole cebrini temel alır. Bu sistemde yer alan “1” ve “0”, sırasıyla açık (İngilizcesi: ON) ve kapalı (İngilizcesi: OFF) devrelerle eş anlamlıdır. Sayısal bilgisayar devreleri uygulamasında, ikili değişkenler üzerinde tanımlanan sayısal operasyonları gösterir.
Postulatlar
[değiştir | kaynağı değiştir]Boolean cebri 10 temel postulata dayanır. 0 ve 1 sayıları nedeniyle her postulat çift olarak ifade edilir. Postulatların 0 ve 1 karakterlerini kapsaması nedeniyle bunların açıklaması genellikle kapalı ve açık elektrik devreleri ile yapılır.
Postulat 1: 0.0=0 Postulat 2: 0.1=0 Postulat 3: 1.0=0 Postulat 4: 1.1=1 Postulat 5: 0'=1 Postulat 6: 1+1=1 Postulat 7: 0+1=1 Postulat 8: 1+0=1 Postulat 9: 0+0=0 Postulat 10: 1'=0
Teoremler
[değiştir | kaynağı değiştir]Boolean Cebri, 10 teoremden oluşur.
Değişme Kuralı
[değiştir | kaynağı değiştir]A+B=B+A A.B=B.A
Birleşme Kuralı
[değiştir | kaynağı değiştir]A+B+C=(A+B)+C=A+(B+C) A.B.C=(A.B).C=A.(B.C)
Aynı Kuvvet Kuralı(özdeşlik kanunu)
[değiştir | kaynağı değiştir]A.A=A A+A=A
0+0=0 0.0=0 1.1=1
ve (and) kanunu
[değiştir | kaynağı değiştir]A.1=A
A.0=0
veya (or) kanunu
[değiştir | kaynağı değiştir]A+1=1
A+0=A
Etkisiz Eleman Kuralı
[değiştir | kaynağı değiştir]A.1=A A+0=A
Tamamlayıcı Kural
[değiştir | kaynağı değiştir]A.A'=0 A'+A=1
Yutma Kuralı
[değiştir | kaynağı değiştir]A.(A+B)=A A+(AB)=A
Dağılma Kuralı
[değiştir | kaynağı değiştir]A(B+C)=(AB)+(AC) A+(B.C)=(A+B)(A+C)
Çift Tersleme Kuralı ( Tersin Tersi )
[değiştir | kaynağı değiştir](A')'=A [(A+B)']'=A+B
(A.B)'=A'+B' (A+B)'=A'.B'
Semboller
[değiştir | kaynağı değiştir]Sayısal olarak bir değişken veya fonksiyon iki değer alabilir. Bu değerler 1 veya 0 olacaktır. Değişkenlerin veya fonksiyonların aldığı bu değerler sayısal devrelerde eğer “1” ise YÜKSEK gerilim seviyesi, “0” ise ALÇAK gerilim seviyesini gösterecektir.
Değil veya tümleyen (komplement), boolean matematiğinde değişkenin üzerine çizilen bir çizgi ile gösterilir. Örneğin A’ ifadesi “ A’ nın değili veya A’nın komplementi” şeklinde okunur. Eğer A=1 ise A’=0, A=0 ise A’ =1 olur. Tümleyen(komplement) veya değil için A’ şeklinde yazım kullanılabilir.
A ve B girişlere uygulanan iki değişkeni gösterirse VE fonksiyonu Boolean ifadesi olarak ‘A.B’ şeklinde yazılırken vEYA fonksiyonu için ‘A+B’ eklinde yazılacaktır.
Elektronik mantık kapıları
[değiştir | kaynağı değiştir]Diyotla yapılan AND ve OR kapıları
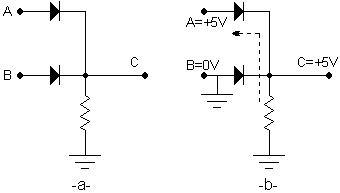
Şekil 1.13a 'da diyotlarla AND lojiğinin elde edilmesi görülmektedir. Şekil 1.13d 'de görüldüğü gibi A ve B girişlerinin biri 0 volt (şase) yapılacak olursa, devre akımı doğru polarmalanmış diyot üzerinden ok yönünde devresini tamamlayacağından çıkış gerilimi C, 0 volt olur.
A ve B girişleri +5V yapıldığında diyotlar ters polarmalandığından yalıtkan olacak ve 5V 'luk gerilim şekil 1.13e 'de görüldüğü gibi C çıkışında görülecektir. Bu durum bize AND işlemini verir, yani A ve B girişi 1 olduğunda çıkış 1 olur. Girişlerden biri 0 olduğunda çıkış 0 olur. Bu işlemin doğruluk tabloları gerilim olarak şekil 1.13d 'de, lojik olarak şekil 1.13e 'de görülmektedir.
A B C 0V 0V 0V 0V +5V 0V +5V 0V 0V +5V +5V +5V
-d-
A B C 0 0 0 0 1 0 1 0 0 1 1 1
-e-
0V = Lojik 0 +5V = Lojik 1
Şekil 1.14a 'da diyotlarla OR Lojiğinin elde edilmesi görülmektedir. Şekil 1.14b 'de görüldüğü gibi A ve B girişlerinden biri +5V yapılacak olursa girişe verilen uca bağlı diyot iletken olacağından +5V C çıkışında görülür. A ve B girişleri aynı anda 0V yapılırsa her iki diyotta yalıtkan olacağından C çıkışıda 0V olacaktır. Şekil1.4c 'de gerilim olarak, şekil1.14d 'de ise lojik olarak OR işleminin doğruluk tabloları görülmektedir.
A B C 0V 0V 0V 0V +5V +5V +5V 0V +5V +5V +5V +5V
-c-
A B C 0 0 0 0 1 1 1 0 1 1 1 1
-d-
0V = Lojik 0 +2,4 - +5V = Lojik 1
a) Ve (And) kapısı
[değiştir | kaynağı değiştir]Ve kapısı iki veya daha fazla giriş ve bir adette çıkış ucuna sahiptir. Bu giriş uçlarına uygulanan 1 veya 0 kodlarına göre çıkışta değişiklikler görülür. Ve kapısının tüm girişleri 1 olduğunda çıkış 1, herhangi bir ucu 0 olduğunda ise çıkış 0'dır. Kapı hesaplarındaki formülü Q (Çıkış (C)) = A . B dir. Aşağıda Ve kapısının sembolü ve iç yapısı görülmektedir.
b) Ve Değil (Nand) kapısı
[değiştir | kaynağı değiştir]Değil mantığı tüm kapılarda vardır. Bu kapılar normal kapıların çıkış uçlarına değil kapısı eklenerek elde edilirler. Yani Ve kapısının çıkış ucu 1 olduğu durumlarda Ve Değil kapısının çıkışı 0, 0 olduğu durumlarda ise 1'dir. Kapı hesaplarındaki formülü Q (Çıkış (C)) = (A . B)' dir. Üst tırnak işareti, değili (tersi) manasına gelmektedir. Formülün sonucu 1 ise 0, 0 ise de 1 'dir. Aşağıda Ve Değil kapısının sembolü ve iç yapısı görülmektedir.
c) Veya (Or) kapısı
[değiştir | kaynağı değiştir]Veya kapısı da iki veya daha fazla giriş, bir adette çıkış ucuna sahiptir. Giriş uçlarından herhangi birisinin 1 olması durumunda çıkış 1, diğer durumlarda da çıkış 0'dır. Yani Ve kapısının tersi mantığında çalışır. Kapı hesaplarındaki formülü Q (Çıkış (C)) = A + B dir.
d) Veya Değil (Nor) kapısı
[değiştir | kaynağı değiştir]Veya Değil kapısı da yine Veya kapısının çıkış ucuna Değil eklenerek elde edilmiştir. Veya Değil kapısının çıkış durumları Veya kapısının çıkış durumlarının tam tersidir. Kapı hesaplarındaki formülü Q (Çıkış (C)) = (A + B)' dir.
e) Özel Veya kapısı
[değiştir | kaynağı değiştir]İsminin Özel Veya kapısı olmasına rağmen Veya kapısı ile hiçbir alakası yoktur. Özel Veya kapısının girişleri aynı olduğunda çıkış 0, girişleri farklı olduğunda ise çıkış 1 'dir. Yani girişler 1 0 ya da 0 1 iken çıkış 1, girişler 0 0 ya da 1 1 iken de çıkış 0 'dır. Hesaplardaki formülü ise Q = A Å B dir.
f) Özel Veya Değil kapısı
[değiştir | kaynağı değiştir]Özel Veya Değil kapısı da Özel Veya Kapısının Çıkışına Değil eklenmiş halidir. Giriş uçları aynı iken çıkış 1, giriş uçları farklı iken de çıkış 0 'dır. Hesaplamalardaki formülü Q = (A Å B)' dir.
g) Değil kapısı
[değiştir | kaynağı değiştir]Değil Kapısı bir giriş ve bir de çıkış ucuna sahiptir. Girişine gelen Binary kodu tersleyerek çıkışına iletir. Yani giriş 1 iken çıkış 0, giriş 0 iken çıkış 1 'dir. Hesaplamalardaki formülü Q = A' şeklindedir. Aşağıda Değil kapısının sembolü ve iç yapısı görülmektedir.
Boolean matematiği tamamen 1 ve 0 üzerine kurulu bir matematiktir. Bu 1 ve 0, düşük - yüksek, var - yok, olumlu - olumsuz, gibi terimlere benzetilebilir. Boolean matematiğinde, (') işareti tersi, (.) işareti Ve, (+) işareti Veya, (Å) işareti de özel veya manasına gelmektedir.