Reynolds sayısı

Bir mum alevinden yükselen dumanın gösterildiği bu görselde laminer akıştan türbülanslı akışa geçilmektedir.

Bir silindirin etrafında oluşan bir girdap sokağı (İng. vortex street). Bu, herhangi bir akışkan, silindir boyutu ve akışkan hızı için, Reynolds sayısının yaklaşık 40 ile 1000 arasında olduğu durumlarda silindirler ve küreler etrafında meydana gelebilir.

George Stokes, Reynolds sayısını tanıttı.

Osborne Reynolds, bu kavramı popüler hale getirdi.

Akışkanlar dinamiği alanında, Reynolds sayısı (Re), farklı durumlarda akışkan akışı desenlerini tahmin etmeye yardımcı olan bir boyutsuz sayıdır ve eylemsizlik kuvvetleri ile viskoz kuvvetler arasındaki oranı ölçer. Düşük Reynolds sayılarında, akışlar genellikle laminer akış tarafından domine edilirken, yüksek Reynolds sayılarında akışlar genellikle türbülanslı olur. Türbülans, akışkanın hız ve yönündeki farklılıklardan kaynaklanır ve bazen bu yönler kesişebilir veya akışın genel yönüne ters hareket edebilir (girdap akımları (İng. eddy)). Bu girdap akımları, akışı karıştırmaya başlar ve bu süreçte enerji tüketir, bu da sıvılarda kavitasyon olasılığını artırır.

Reynolds sayısının, bir borudaki sıvı akışından bir uçak kanadının üzerinden geçen hava akışına kadar geniş uygulama alanları vardır. Laminer akıştan türbülanslı akışa geçişi tahmin etmek ve rüzgar tünelinde bir uçak modeli ile tam boyutlu versiyonu gibi benzer ama farklı büyüklükteki akış durumlarının ölçeklendirilmesinde kullanılır. Türbülansın başlangıcını tahmin etme ve ölçeklendirme etkilerini hesaplama yeteneği, yerel veya küresel hava veya su hareketlerinde akışkan davranışını tahmin etmeye yardımcı olabilir ve dolayısıyla ilgili meteorolojik ve klimatolojik etkileri öngörebilir.

Bu kavram, 1851 yılında George Stokes tarafından tanıtılmıştır, ancak Reynolds sayısı, 1908 yılında Arnold Sommerfeld tarafından Osborne Reynolds (1842–1912) onuruna adlandırılmıştır; Reynolds, 1883 yılında bu sayının kullanımını yaygınlaştırmıştır.

Tanım

Reynolds sayısı, farklı akışkan hızları nedeniyle göreceli iç hareketlere maruz kalan bir akışkan içinde eylemsizlik kuvvetlerinin viskoz kuvvetlere oranıdır. Bu kuvvetlerin davranışlarının değiştiği bir bölge, sınır tabakası (İng. boundary layer) olarak bilinir, örneğin bir borunun iç yüzeyi gibi. Benzer bir etki, yüksek hızlı bir akışkanın düşük hızlı bir akışkana girişi ile yaratılır; örneğin, havada bir alevden yayılan sıcak gazlar. Bu göreceli hareket, türbülanslı akışın gelişmesinde bir faktör olan akışkan sürtünmesi oluşturur. Bu etkiye karşı koyan faktör ise akışkanın viskozitesidir, bu da türbülansı engellemeye eğilimlidir. Reynolds sayısı, belirli akış koşulları için bu iki tür kuvvetin göreceli önemini nicelendirir ve belirli bir durumda türbülanslı akışın ne zaman meydana geleceğine dair bir rehberdir.

Türbülanslı akışın başlangıcını tahmin etme yeteneği, boru sistemleri veya uçak kanatları gibi ekipmanların tasarımı için önemli bir araçtır. Bunun yanı sıra, Reynolds sayısı akışkan dinamiği problemlerinin ölçeklendirilmesinde de kullanılır ve bir model uçak ile tam boyutlu versiyonu gibi iki farklı akış durumu arasındaki dinamik benzeşimi (İng. dynamic similtude) belirler. Bu tür ölçeklendirme doğrusal değildir ve her iki duruma da Reynolds sayılarının uygulanması, ölçeklendirme faktörlerinin geliştirilmesine olanak tanır.

Laminer ve türbülanslı akış rejimleri ile ilgili olarak:

• Laminer akış, viskoz kuvvetlerin baskın olduğu düşük Reynolds sayılarında meydana gelir ve uniform, sabit akışkan hareketi ile karakterize edilir;
• Türbülanslı akış, eylemsizlik kuvvetlerinin baskın olduğu yüksek Reynolds sayılarında meydana gelir ve kaotik girdaplar, vorteksler ve diğer akış kararsızlıklarını üretme eğilimindedir.

Reynolds sayısı şu şekilde tanımlanır

$\mathrm {Re} ={\frac {uL}{\nu }}={\frac {\rho uL}{\mu }}$

burada:

• ρ akışkanın yoğunluk değeridir (SI birimleri: kg/m³)
• u akış hızının değeridir (m/s)
• L karakteristik uzunluktur (m)
• μ akışkanın dinamik viskozitesidir (Pa·s veya N·s/m² veya kg/(m·s))
• ν akışkanın kinematik viskozitesidir (m²/s).

Brezina denklemi

Reynolds sayısı, bir akışkanın bir yüzeye göre göreceli hareket ettiği çeşitli durumlar için tanımlanabilir. Bu tanımlar genellikle yoğunluk ve viskozite gibi akışkan özelliklerini, bir hızı ve bir karakteristik uzunluk veya karakteristik boyutu (yukarıdaki denklemde L) içerir. Bu boyut, konvansiyona bağlıdır—örneğin, küreleri veya daireleri tanımlamak için yarıçap ve çap eşit derecede geçerlidir, ancak biri konvansiyon gereği seçilir. Uçaklar veya gemiler için uzunluk veya genişlik kullanılabilir. Bir borudaki akış veya bir akışkan içinde hareket eden bir küre için, bugün genellikle iç çap kullanılır. Dikdörtgen borular veya küresel olmayan nesneler gibi diğer şekiller için bir eşdeğer çap tanımlanmıştır. Sıkıştırılabilir gazlar gibi değişken yoğunluklu akışkanlar veya Newtonyen olmayan akışkanlar gibi değişken viskoziteli akışkanlar için özel kurallar geçerlidir. Hız da bazı durumlarda konvansiyona bağlı olabilir, özellikle karıştırılmış kaplarda.

Pratikte, yalnızca Reynolds sayısını eşleştirmek, benzerliği sağlamak için yeterli değildir. Akışkan akışı genellikle kaotiktir ve sınırlayıcı yüzeylerin şekil ve yüzey pürüzlülüğündeki çok küçük değişiklikler çok farklı akışlar oluşturabilir. Bununla birlikte, Reynolds sayıları çok önemli bir rehberdir ve geniş çapta kullanılmaktadır.

Türetim

Bir fiziksel sistemde ilgili fiziksel büyüklüklerin sadece $\rho ,u,L,\mu$ olduğunu biliyorsak, Reynolds sayısı esasen Buckingham π teoremi ile belirlenir.

Detaylı olarak incelendiğinde, $\rho ,u,L,\mu$ olmak üzere 4 büyüklük vardır, ancak bunlar sadece 3 boyuta (uzunluk, zaman, kütle) sahiptir. $\rho ^{x_{1}}u^{x_{2}}L^{x_{3}}\mu ^{x_{4}}$ ifadesini düşünebiliriz, burada $x_{1},...,x_{4}$ reel sayılardır. $\rho ^{x_{1}}u^{x_{2}}L^{x_{3}}\mu ^{x_{4}}$'nın üç boyutunu sıfıra ayarladığımızda, 3 bağımsız lineer kısıt elde ederiz ve bu nedenle çözüm uzayı 1 boyuta sahiptir ve $(1,1,1,-1)$ vektörü tarafından kapsanmaktadır.

Bu nedenle, $\rho ,u,L,\mu$ kullanılarak oluşturulan herhangi bir boyutsuz büyüklük, Reynolds sayısı olan $\rho uL\mu ^{-1}$'in bir fonksiyonudur.

Alternatif olarak, sıkıştırılamaz Navier–Stokes denklemlerini (konvektif form) kullanabiliriz:

$${\frac {\partial \mathbf {u} }{\partial t}}+(\mathbf {u} \cdot \nabla )\mathbf {u} -\nu \,\nabla ^{2}\mathbf {u} =-{\frac {1}{\rho }}\nabla p+\mathbf {g}$$

Yerçekimi terimi ${\mathbf {g}}$'yi kaldırdığımızda, sol tarafta eylemsizlik kuvveti ${\frac {\partial \mathbf {u} }{\partial t}}+(\mathbf {u} \cdot \nabla )\mathbf {u}$ ve viskoz kuvvet $\nu \,\nabla ^{2}\mathbf {u}$ kalır.

Bunların oranı ${\frac {(\mathbf {u} \cdot \nabla )\mathbf {u} }{\nu \,\nabla ^{2}\mathbf {u} }}\sim {\frac {u^{2}/L}{\nu u/L^{2}}}={\frac {uL}{\nu }}$ mertebesindedir, bu da Reynolds sayısıdır.

Alternatif türetme

Reynolds sayısı, Newtonyen bir akışkan için sıkıştırılamaz Navier–Stokes denklemlerinin boyutsuz sayı formu kullanılarak elde edilebilir ve Lagrange türevi cinsinden ifade edilir:

$\rho {\frac {D\mathbf {v} }{Dt}}=-\nabla p+\mu \nabla ^{2}\mathbf {v} +\rho \mathbf {f} .$

Yukarıdaki denklemdeki her terim, birim hacim başına kuvvet birimine sahip bir "cisim kuvveti" (İng. body force) birimlerine sahiptir ve bir yoğunluk ile bir ivmenin çarpımı olan aynı boyutlara sahiptir. Bu nedenle, her terim bir akışın kesin ölçümlerine bağlıdır. Denklemi boyutsuz hale getirdiğimizde, yani denklemi ters birimlerle çarptığımızda, fiziksel boyutlara doğrudan bağlı olmayan bir form elde ederiz. Boyutsuz bir denklem elde etmenin bir yolu, tüm denklemi şu faktörle çarpmaktır:

${\frac {L}{\rho V^{2}}},$

burada

• V akışkana göre ortalama hızdır, v veya v, (m/s),
• L karakteristik uzunluktur (m),
• ρ akışkan yoğunluğudur (kg/m³).

Eğer şimdi

${\begin{aligned}\mathbf {v} '&={\frac {\mathbf {v} }{V}},&p'&=p{\frac {1}{\rho V^{2}}},&\mathbf {f} '&=\mathbf {f} {\frac {L}{V^{2}}},&{\frac {\partial }{\partial t'}}&={\frac {L}{V}}{\frac {\partial }{\partial t}},&\nabla '&=L\nabla ,\end{aligned}}$

olarak ayarlarsak, Navier-Stokes denklemini boyutsuz olarak yeniden yazabiliriz:

${\frac {D\mathbf {v} '}{Dt'}}=-\nabla 'p'+{\frac {\mu }{\rho LV}}\nabla '^{2}\mathbf {v} '+\mathbf {f} ',$

burada μ/ρLV = 1/Re terimi yer almaktadır.

Son olarak, okuma kolaylığı sağlamak amacıyla üst simgeleri kaldırdığımızda:

${\frac {D\mathbf {v} }{Dt}}=-\nabla p+{\frac {1}{\mathrm {Re} }}\nabla ^{2}\mathbf {v} +\mathbf {f} .$

Evrensel sedimantasyon denklemi — sürükleme katsayısı, Reynolds sayısı ve şekil faktörünün bir fonksiyonu, 2D diyagram

Evrensel sedimantasyon denklemi — sürükleme katsayısı, Reynolds sayısı ve şekil faktörünün bir fonksiyonu, 3D diyagram

Bu nedenle, aynı Reynolds sayısına sahip tüm Newtonyen, sıkıştırılamaz akışlar matematiksel olarak karşılaştırılabilir. Ayrıca, yukarıdaki denklemde Re → ∞ olduğunda viskoz terimlerin ortadan kalktığına dikkat edin. Bu nedenle, yüksek Reynolds sayısına sahip akışlar, serbest akışta yaklaşık olarak viskozitesizdir.

Tarihçe

Osborne Reynolds'ın türbülanslı akışın başlangıcını gösteren 1883 tarihli düzeni. Düzenek hala Manchester Üniversitesi'ndedir.

Reynolds'ın 1883 tarihli makalesinden türbülanslı akışın başlangıcını gösteren diyagram.

Osborne Reynolds, akışkanın borulardaki akışının laminer akıştan türbülanslı akışa geçiş koşullarını kapsamlı bir şekilde inceledi. 1883 tarihli makalesinde, laminer akıştan türbülanslı akışa geçişi tanımladığı klasik bir deneyde, büyük bir borunun merkezine renklendirilmiş küçük bir su akımı vererek suyun farklı akış hızları altındaki davranışını inceledi.

Gözlem yapmak için büyük boru camdan yapılmıştı. Borunun sonunda, boru içindeki su hızını değiştirmek için bir akış kontrol vanası vardı. Düşük hızlarda, renklendirilmiş akış boru boyunca belirginliğini korudu. Hız arttığında, belirli bir noktada akış bozuldu ve akışkanın kesiti boyunca yayıldı. Bu olayın gerçekleştiği nokta, laminer akıştan türbülanslı akışa geçiş noktasıydı.

Bu deneylerden, dinamik benzerlik için eylemsizlik kuvvetlerinin viskoz kuvvetlere oranı olarak boyutsuz Reynolds sayısı ortaya çıktı. Reynolds ayrıca türbülanslı akışların ortalamasını yapmayı önerdi, bu günümüzde Reynolds ortalaması olarak bilinir. Bu ortalamada hız gibi büyüklükler ortalama ve dalgalanan bileşenlerin toplamı olarak ifade edilir. Bu tür bir ortalama, türbülanslı akışın 'genel' tanımına olanak tanır.

Boru akışı

Bir boru veya tüpte akış için, Reynolds sayısı genellikle şu şekilde tanımlanır:

$\mathrm {Re} ={\frac {uD_{\text{H}}}{\nu }}={\frac {\rho uD_{\text{H}}}{\mu }}={\frac {\rho QD_{\text{H}}}{\mu A}}={\frac {WD_{\text{H}}}{\mu A}},$

burada

• D_H borunun hidrolik çapıdır (boru dairesel ise iç çap) (m),
• Q debidir (m³/s),
• A borunun kesit alanıdır (A = πD²/4) (m²),
• u akışkanın ortalama hızıdır (m/s),
• μ (mu) akışkanın dinamik viskozitesidir (Pa·s = N·s/m² = kg/(m·s)),
• ν (nu) kinematik viskozitedir (ν = μ/ρ) (m²/s),
• ρ (rho) akışkanın yoğunluğudur (kg/m³),
• W akışkanın kütlesel akış hızıdır (kg/s).

Yüksekliği ve genişliği karşılaştırılabilir olan kare, dikdörtgen veya halka şeklindeki kanallar gibi şekiller için, iç akış durumlarında karakteristik boyut, hidrolik çap D_H olarak alınır ve şu şekilde tanımlanır:

$D_{\text{H}}={\frac {4A}{P}},$

burada A kesit alanı ve P ıslak çevredir. Bir kanalın ıslak çevresi, akışla temas halinde olan tüm kanal duvarlarının toplam çevresidir. Bu, kanalın havaya maruz kalan uzunluğunun ıslak çevreye dahil olmadığı anlamına gelir.

Dairesel bir boru için hidrolik çap, borunun iç çapına tam olarak eşittir:

$D_{\text{H}}=D.$

Bir boru içinde boru gibi bir halka kanal için, hidrolik çapın şu şekilde azaldığı cebirsel olarak gösterilebilir:

$D_{\text{H,annulus}}=D_{\text{o}}-D_{\text{i}},$

burada

• D_o dış borunun iç çapıdır,
• D_i iç borunun dış çapıdır.

Dairesel olmayan kanallarda akış hesaplamaları için, kanal kesitinin en-boy oranı AR, 1/4 < AR < 4 aralığında kaldığı sürece, hidrolik çap, dairesel bir kanalın çapı yerine makul bir doğrulukla kullanılabilir.

Laminer-türbülans geçişi

Sınır tabakası akışında düz bir plaka üzerinde yapılan deneyler, belirli bir akış mesafesinden sonra laminer sınır tabakasının kararsız hale gelip türbülanslı hale geleceğini doğrulamaktadır. Bu kararsızlık, genellikle Re_x ≈ 5×10⁵ olduğunda farklı ölçeklerde ve farklı akışkanlarla meydana gelir. Burada x düz plakanın ön kenarından olan mesafeyi ifade eder ve akış hızı sınır tabakası dışındaki akışkanın serbest akış (İng. freestream) hızıdır.

Çapı D olan bir borudaki akış için deneysel gözlemler, "tamamen gelişmiş" akış durumunda, laminer akışın Re_D < 2300 olduğunda ve türbülanslı akışın Re_D > 2900 olduğunda meydana geldiğini göstermektedir. Bu aralığın alt ucunda, sürekli bir türbülanslı akış oluşacak, ancak borunun girişinden çok uzun bir mesafede olacaktır. Aradaki akış, laminerden türbülansa ve ardından tekrar laminer akışa düzensiz aralıklarla geçmeye başlayacaktır; bu duruma kesintili akış (İng. intermittent flow) denir. Bu, borunun kesitinin farklı bölgelerindeki akışkanın farklı hızları ve koşulları nedeniyle oluşur, boru pürüzlülüğü ve akışın uniformluğu gibi diğer faktörlere bağlıdır. Laminer akış, borunun hızlı hareket eden merkezinde baskın olma eğilimindeyken, yavaş hareket eden türbülanslı akış borunun duvarına yakın bölgede baskındır. Reynolds sayısı arttıkça, sürekli türbülanslı akış girişe daha yakın hale gelir ve kesintili akış artar, ta ki akış tamamen türbülanslı hale gelene kadar (Re_D > 2900). Bu sonuç, hidrolik çap kullanılarak dairesel olmayan kanallara genellenebilir ve diğer kanal şekilleri için bir geçiş Reynolds sayısının hesaplanmasına olanak tanır.

Bu geçiş Reynolds sayıları, kritik Reynolds sayıları olarak da adlandırılır ve 1895 civarında Osborne Reynolds tarafından incelenmiştir. Kritik Reynolds sayısı, her geometri için farklıdır.

Geniş-kanal akışı

İki düz paralel yüzey arasında hareket eden bir akışkan için - genişliğin plakalar arasındaki mesafeden çok daha büyük olduğu durumlarda - karakteristik boyut, plakalar arasındaki mesafeye eşittir. Bu, yukarıda belirtilen halka kanal ve dikdörtgen kanal durumlarıyla, sınırlayıcı bir en-boy oranına alındığında, tutarlıdır.

Açık-kanal akışı

Serbest yüzeyli bir sıvının akışını hesaplamak için hidrolik yarıçapın belirlenmesi gerekmektedir. Bu, kanalın kesit alanının ıslak çevresine bölünmesiyle elde edilir. Yarı dairesel bir kanal için, tam boru akış durumunda, hidrolik yarıçap çapın dörtte biridir. Dikdörtgen bir kanal için, hidrolik yarıçap, kesit alanının ıslak çevresine bölünmesiyle hesaplanır. Bazı kaynaklarda, türbülans başlangıcı için boru akışında olduğu gibi aynı Re değerini veren hidrolik yarıçapın dört katı bir karakteristik boyut kullanılır, diğer kaynaklarda ise, geçiş ve türbülanslı akış için farklı Re değerleri ile sonuçlanan hidrolik yarıçap karakteristik uzunluk ölçeği olarak kullanılır.

Kanat profili etrafında akış

Reynolds sayıları, kanat profili tasarımında, karakteristikleri hesaplama ve kıyaslama sırasında "ölçek etkisini" yönetmek için kullanılır (küçük bir kanat, büyük boyutta ölçeklendirildiğinde farklı performans gösterecektir). Akışkan dinamiği uzmanları, kanat profili Reynolds sayısını R = Vc/ν olarak tanımlar, burada V uçuş hızı, c kanat profili uzunluğu ve ν kanat profilinin içinde bulunduğu akışkanın kinematik viskozitesidir; deniz seviyesinde atmosfer için bu değer 1,460×10^-5 m²/s'dir. Bazı özel çalışmalarda, kanat profili uzunluğu dışında bir karakteristik uzunluk kullanılabilir; nadir durumlarda "kanat açıklığı Reynolds sayısı" kullanılır, ancak bu, kanadın açıklık yönündeki istasyonlarıyla karıştırılmamalıdır, burada hala kanat profili uzunluğu kullanılır.

Akışkan-içi nesne

Balın yüksek viskozitesi, bir kovadan dökülürken mükemmel bir laminer akış sağlar, düşük yüzey gerilimi ise altındaki akışkana ulaştıktan sonra bile tabaka halinde kalmasını sağlar. Türbülansa benzer şekilde, akış dirençle karşılaştığında yavaşlar ve ileri geri salınmaya başlar, kendisi üzerinde yığılır.

Akışkan içinde hareket eden bir nesne için Reynolds sayısı, partikül Reynolds sayısı olarak adlandırılır ve genellikle Re_p ile gösterilir; bu, çevresindeki akışın doğasını ve düşüş hızını karakterize eder.

Viskoz akışkanlar

Düşen bir küre etrafındaki sürünme akışı: akım çizgileri, sürükleme kuvveti F_d ve yerçekimi kuvveti F_g.

Viskozitenin doğal olarak yüksek olduğu yerlerde, örneğin polimer çözeltileri ve polimer eriyikleri, akış genellikle laminer olur. Reynolds sayısı çok küçüktür ve Stokes yasası akışkanın viskozitesini ölçmek için kullanılabilir. Kürelerin akışkan içinden düşmesine izin verilir ve küreler hızla terminal hıza ulaşır, bu hızdan viskozite belirlenebilir.

Polimer çözeltilerinin laminer akışı, balıklar ve yunuslar gibi hayvanlar tarafından, yüzme sırasında vücutları üzerinden akışı kolaylaştırmak için derilerinden viskoz çözeltiler salgılayarak kullanılmaktadır. Yat yarışlarında, sahipleri hız avantajı elde etmek için gövdenin ıslak yüzeyine düşük moleküler ağırlıklı polietilen glikol gibi bir polimer çözeltisi pompalayarak kullanmışlardır.

Ancak, polimerlerin karıştırılması için bir sorun teşkil eder, çünkü ince dolgu maddesini (örneğin) malzeme boyunca dağıtmak için türbülans gereklidir. "Boşluk transfer karıştırıcısı" (İng. "cavity transfer mixer") gibi icatlar, hareketli bir eriyiğe birçok katlama yaparak karıştırma verimliliğini artırmak için geliştirilmiştir. Bu cihaz, karıştırmaya yardımcı olmak için ekstrüderlere monte edilebilir.

Akışkan-içi küre

Bir kürenin sürükleme katsayısı C_d, Reynolds sayısı Re'nin bir fonksiyonu olarak, laboratuvar deneylerinden elde edilmiştir. Koyu çizgi, yüzeyi düzgün bir küre içindir, açık çizgi ise pürüzlü yüzeye sahip bir küre (örneğin küçük çukurlar) içindir. Pürüzlü yüzeye sahip bir golf topunun belirli akışkan hızlarında, düzgün bir topa göre daha az sürüklenme yaşadığı bir aralık vardır. Çizgi boyunca yer alan sayılar, çeşitli akış rejimlerini ve sürükleme katsayısındaki ilgili değişiklikleri göstermektedir:

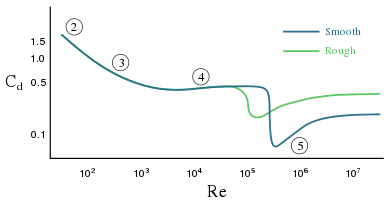
2. yapışık akış (İng. attached flow) (Stokes akışı) ve durağan ayrılmış akış,
3. ayrılmış kararsız akış, ayrılmanın yukarısında bir laminer akış sınır tabakası ile ve bir vorteks sokağı üreterek,
4. ayrılmış kararsız akış, akış ayrılmasından önce yukarı akış tarafında laminer bir sınır tabakası ile, kürenin aşağı akışında kaotik türbülanslı iz (İng. wake) ile,
5. kritik sonrası ayrılmış akış, türbülanslı bir sınır tabakası ile.

Bir akışkan içinde bir küre için, karakteristik uzunluk ölçeği kürenin çapıdır ve karakteristik hız, kürenin akışkana göre olan hızıdır; bu hız, kürenin hareketinin bu referans akışkan parselini bozmadığı bir mesafede ölçülür. Yoğunluk ve viskozite, akışkana ait olan değerlerdir. Bu tanıma göre, tamamen laminer akışın yalnızca Re = 10'a kadar mevcut olduğunu hatırlanmalıdır.

Yüksek Reynolds sayılarında bir küre üzerindeki sürükleme, yüzey pürüzlülüğüne bağlıdır. Örneğin, bir golf topunun yüzeyine çukurlar eklemek, topun yukarı akış tarafındaki sınır tabakasının laminerden türbülansa geçmesine neden olur. Türbülanslı sınır tabakası, laminer bir sınır tabakasından çok daha uzun süre topun yüzeyine bağlı kalabilir ve böylece daha dar bir düşük basınçlı iz bölgesi (İng. wake) oluşturur ve dolayısıyla daha az basınç sürüklenmesi yaratır. Basınç sürüklenmesindeki azalma, topun daha uzağa gitmesine neden olur.

Akışkan-içi dikdörtgen nesne

Dikdörtgen bir nesne için denklem, nesnenin bir elipsoit olarak yaklaşıldığı ve uzunluk ekseninin karakteristik uzunluk ölçeği olarak seçildiği durumda küreninkine benzerdir. Bu tür düşünceler, örneğin doğal akarsularda, tamamen küre-şekilli zerrecik çok az olduğu durumlarda önemlidir. Her eksenin ölçümünün pratik olmadığı zerrecikler için, karakteristik parçacık uzunluk ölçeği olarak elekten geçen çaplar kullanılır. Her iki yaklaşım da kritik Reynolds sayısının değerlerini değiştirir.

Düşme hızı

Parçacık Reynolds sayısı, bir parçacığın düşme hızını belirlemede önemlidir. Parçacık Reynolds sayısı laminer akışı gösterdiğinde, Stokes yasası kullanılarak parçacığın düşme hızı veya çökelme hızı hesaplanabilir. Parçacık Reynolds sayısı türbülanslı akışı gösterdiğinde, uygun çökelme hızını modellemek için türbülanslı bir sürüklenme yasası oluşturulmalıdır.

Dolgulu yatak

Yaklaşık çapı D olan küresel parçacıkların temas halinde bulunduğu bir yataktan akışkan akışı için, boşluk oranı ε ve görünür hız v_s ise, Reynolds sayısı şu şekilde tanımlanabilir:

$\mathrm {Re} ={\frac {\rho v_{\text{s}}D}{\mu }},$

veya

$\mathrm {Re} ={\frac {\rho v_{\text{s}}D}{\mu \varepsilon }},$

veya

$\mathrm {Re} ={\frac {\rho v_{\text{s}}D}{\mu (1-\varepsilon )}}.$

Denklem seçimi ilgili sisteme bağlıdır: birinci denklem, çeşitli doldurulmuş ve akışkan yatak türleri için verileri ilişkilendirmede başarılıdır; ikinci Reynolds sayısı, sıvı faz verilerine uygundur; üçüncü denklem ise sıvı akışkanlaştırılmış yatak sistemi için ilk kez tanıtılarak akışkan yatak verilerini ilişkilendirmede başarılı bulunmuştur.

Laminer koşullar Re = 10'a kadar geçerlidir, Re = 2000'den itibaren tamamen türbülanslıdır.

Karıştırmalı kap

Merkezi döner bir palet, türbin veya pervane ile karıştırılan silindirik bir kapta (İng. stirred vessel), karakteristik boyut karıştırıcının çapı D'dir. Hız, V ise ND'dir, burada N dönme hızı (rad/s) olarak ifade edilir. Reynolds sayısı şu şekilde olur:

$\mathrm {Re} ={\frac {\rho ND^{2}}{\mu }}={\frac {\rho VD}{\mu }}.$

Sistem, Re değeri 10000'in üzerinde olduğunda tamamen türbülanslıdır.

Boru sürtünmesi

Reynolds sayısı ve göreceli boru pürüzlülüğünün bir fonksiyonu olarak Darcy–Weisbach sürtünme faktörünü f tanımlayan Moody diyagramı.

Tamamen gelişmiş akışkan akışında borulardaki basınç düşüşleri Moody diyagramı kullanılarak tahmin edilebilir. Bu diyagram, Reynolds sayısı Re ve göreceli pürüzlülüğe ε/D karşı Darcy–Weisbach sürtünme faktörünü f çizer. Diyagram, Reynolds sayısı arttıkça laminer, geçiş ve türbülanslı akış rejimlerini açıkça gösterir. Boru akışının doğası, akışın laminer mi yoksa türbülanslı mı olduğuna güçlü bir şekilde bağlıdır.

Akışların benzerliği

Bir silindir üzerindeki akışın nitel davranışları büyük ölçüde Reynolds sayısına bağlıdır; benzer akış desenleri genellikle şekil ve Reynolds sayısı eşleştiğinde ortaya çıkar, ancak yüzey pürüzlülüğü gibi diğer parametreler büyük bir etkiye sahiptir.

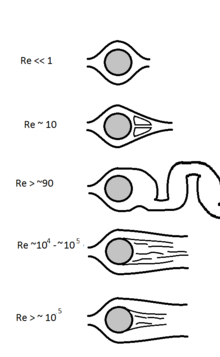
İki akışın benzer olması için aynı geometrilere ve eşit Reynolds ve Euler sayılarına sahip olmaları gerekir. Bir model ve tam ölçekli akıştaki karşılaştırmalı noktaların akışkan davranışlarını karşılaştırırken aşağıdaki durum geçerlidir:

${\begin{aligned}\mathrm {Re} _{\text{m}}&=\mathrm {Re} ,\\\mathrm {Eu} _{\text{m}}&=\mathrm {Eu} ,\end{aligned}}$

burada $\mathrm {Re} _{\text{m}}$ modelin Reynolds sayısı ve $\mathrm {Re}$ tam ölçekli Reynolds sayısıdır ve benzer şekilde Euler sayıları için de geçerlidir.

Model sayıları ve tasarım sayıları aynı oranda olmalıdır, dolayısıyla

${\frac {p_{\text{m}}}{\rho _{\text{m}}v_{\text{m}}^{2}}}={\frac {p}{\rho v^{2}}}.$

Bu, mühendislerin su tünelleri veya rüzgar tüneli gibi ortamlarda küçültülmüş ölçekli modellerle deneyler yapmasına ve verileri gerçek akışlarla ilişkilendirmesine olanak tanır, böylece deney ve laboratuvar süresinden tasarruf sağlar. Gerçek dinamik benzerlik, sıkıştırılabilir akışlarda kullanılan Mach sayısı veya açık kanal akışlarını yöneten Froude sayısı gibi diğer boyutsuz sayıların eşleştirilmesini de gerektirebilir. Bazı akışlar, mevcut cihazlar ve akışkanlarla pratik olarak sağlanabilecekten daha fazla boyutsuz parametre içerir, bu yüzden hangi parametrelerin en önemli olduğuna karar verilmesi gerekir. Deneysel akış modellemesinin faydalı olabilmesi için mühendisin oldukça fazla deneyim ve yargı kabiliyetine sahip olması gerekir.

Yalnızca Reynolds sayısının akışların benzerliği (veya hatta akış rejimi - laminer veya türbülanslı) için yeterli olmadığına dair bir örnek, duvarlar veya diğer sınırlarla sınırlı olan akışlardır. Bunun klasik bir örneği, boyutsuz çevre oranının da önemli olduğu Taylor–Couette akışıdır ve bu ayrımların önemli bir rol oynadığı birçok teknik uygulamadır. Bu kısıtlamaların prensipleri Maurice Marie Alfred Couette ve Geoffrey Ingram Taylor tarafından geliştirilmiş ve daha sonra Floris Takens ve David Ruelle tarafından ilerletilmiştir.

Tipik Reynolds sayısı değerleri

• Dictyostelium amipleri: ~ 1 × 10⁻⁶
• Bakteri ~ 1 × 10⁻⁴
• Ciliate ~ 1 × 10⁻¹
• En küçük balık ~ 1
• Beyindeki kan akışı ~ 1 × 10²
• Aorttaki kan akışı ~ 1 × 10³
• Türbülanslı akışın başlaması ~ 2.3 × 10³ ile 5.0 × 10⁴ arasında boru akışı ve 10⁶ sınır tabakaları için
• Major League Baseball'da tipik bir atış ~ 2 × 10⁵
• Yüzen kişi ~ 4 × 10⁶
• En hızlı balık ~ 1 × 10⁸
• Mavi balina ~ 4 × 10⁸
• Büyük bir gemi (Queen Elizabeth 2) ~ 5 × 10⁹
• Atmosferik tropikal siklon ~ 1 x 10¹²

Türbülanslı akışın en küçük ölçekleri

Türbülanslı bir akışta, zamana bağlı akışkan hareketinin çeşitli ölçekleri mevcuttur. Akışkan hareketinin en büyük ölçeklerinin boyutu (bazen girdaplar olarak adlandırılır), akışın genel geometrisi ile belirlenir. Örneğin, endüstriyel bir baca içinde, akışkan hareketinin en büyük ölçekleri bacanın çapı kadar büyük olabilir. En küçük ölçeklerin boyutu ise Reynolds sayısı ile belirlenir. Reynolds sayısı arttıkça, akışın daha küçük ve daha küçük ölçekleri gözlemlenebilir hale gelir. Bir bacada, dumanın büyük hacimli girdapların yanı sıra çok küçük hız bozulmaları veya girdaplara sahip olduğu görülebilir. Bu anlamda, Reynolds sayısı akıştaki ölçeklerin aralığının bir göstergesidir. Reynolds sayısı ne kadar yüksekse, ölçek aralığı o kadar geniştir. En büyük girdaplar her zaman aynı boyutta olacaktır; en küçük girdaplar ise Reynolds sayısı tarafından belirlenir.

Bu olgunun açıklaması nedir? Yüksek Reynolds sayısı, akışın büyük ölçeklerinde viskoz kuvvetlerin önemli olmadığını gösterir. Eylemsizlik kuvvetlerinin viskoz kuvvetler üzerinde baskın olduğu durumda, akışkan hareketinin büyük ölçekleri sönümlenmez—hareketlerini dağıtacak yeterli viskozite yoktur. Kinetik enerji, bu büyük ölçeklerden giderek daha küçük ölçeklere "kaskat" yapmak zorundadır, ta ki ölçeğin yeterince küçük olduğu bir seviyeye ulaşana kadar; bu seviyede viskoz kuvvetler önemli hale gelir (yani viskoz kuvvetler eylemsizlik kuvvetleri mertebesine gelir). Enerjinin viskoz etkilerle dağılımı nihayet bu küçük ölçeklerde gerçekleşir. Reynolds sayısı, bu viskoz dağılımın hangi ölçekte gerçekleştiğini gösterir.

Fizyoloji

Vücuttaki kan dolaşımı üzerine Poiseuille yasası laminer akışa dayanır. Türbülanslı akışta, akış hızı, laminer akışta basınç gradyanına doğrudan orantılı olmasının aksine, basınç gradyanının karekökü ile orantılıdır.

Reynolds sayısının tanımını kullanarak, büyük çaplı ve hızlı akışın, kanın yoğunluğunun yüksek olduğu durumlarda, türbülansa eğilimli olduğunu görebiliriz. Damar çapındaki ani değişiklikler, örneğin daha dar bir damarın daha geniş bir damara genişlediği durumlarda, türbülanslı akışa yol açabilir. Ayrıca, bir aterom şişkinliği, stetoskopla duyulabilen türbülanslı akışa neden olabilir.

Karmaşık sistemler

Reynolds sayısının yorumu, keyfi karmaşık sistemler alanına genişletilmiştir. Örneğin, finansal akışlar, doğrusal olmayan (İng. nonlinear) ağlar gibi. İkinci durumda, yapay bir viskozite, karmaşık ağ ortamlarında enerjinin dağılımının doğrusal olmayan bir mekanizmasına indirgenir. Reynolds sayısı, açık sınır sistemi için enjekte edilen ve dağıtılan enerji akışları arasındaki dengeyi ifade eden temel bir kontrol parametresini temsil eder. Reynolds kritik rejiminin iki tür faz uzayı hareketini ayırdığı gösterilmiştir: hızlandırıcı (çekici) ve yavaşlatıcı. Yüksek Reynolds sayısı, yalnızca garip çekici (İng. strange attractor) modeli çerçevesinde kaotik rejim geçişine yol açar.

Diğer boyutsuz sayılarla ilişkisi

Akışkanlar mekaniğinde birçok boyutsuz sayı bulunmaktadır. Reynolds sayısı, hız alanındaki yapılar üzerindeki adveksiyon ve difüzyon etkilerinin oranını ölçer ve bu nedenle, bu etkilerin akış tarafından taşınan diğer alanlar (örneğin sıcaklık ve manyetik alanlar) üzerindeki oranını ölçen Péclet sayısı ile yakından ilişkilidir. Re'deki kinematik viskozitenin ν = μ/ρ yerine termal veya manyetik difüzyon katsayısının kullanılması, sırasıyla termal Péclet sayısı ve manyetik Reynolds sayısı ile sonuçlanır. Bu nedenle, bu sayılar, difüzyon katsayılarının oranları olan Prandtl sayısı ve manyetik Prandtl sayısı ile ilişkili yan ürünlerdir.

Dış bağlantılar

• The Reynolds number - The Feynman Lectures on Physics
• The Reynolds Number at Sixty Symbols
• Reynolds mini-biography and picture of original apparatus at Manchester University.
• Reynolds Number Calculation