Hilbert uzayı

Matematikte Hilbert uzayı, sonlu boyutlu Öklit uzayında uygulanabilen lineer cebir yöntemlerinin genelleştirilebildiği ve sonsuz boyutlu da olabilen bir vektör uzayıdır. Daha kesin olarak, bir Hilbert uzayı, uzayın tam metrik uzay olmasını sağlayan bir uzaklık fonksiyonu üreten bir iç çarpımla donatılmış bir vektör uzayıdır. Bir Hilbert uzayı, bir Banach uzayının özel bir durumudur. Matematik, fizik ve mühendislikte sıkça kullanılmaktadır. Kuantum mekaniğiyle uyumludur. Adını David Hilbert'ten almaktadır.
Matematiksel olarak, bir Hilbert uzayı iç çarpım aracılığıyla üstünde norm tanımlanabilen tam normlu vektör uzaydır.[1] En eski Hilbert uzayları, 20. yüzyılın ilk on yılında David Hilbert, Erhard Schmidt ve Frigyes Riesz tarafından incelenmiştir. Kısmi diferansiyel denklemler, kuantum mekaniği, Fourier analizi (sinyal işleme ve ısı transferi uygulamalarını içerir) ve ergodik teori (termodinamiğin matematiksel temelini oluşturur) teorilerinde vazgeçilmez araçlardır. Bu çeşitli uygulamaların çoğunun altında yatan soyut kavram için Hilbert uzayı terimini ortaya atan John von Neumann olmuştur. Hilbert uzayı yöntemlerinin başarısı, fonksiyonel analiz için çok verimli bir dönemin habercisi oldu. Klasik Öklit vektör uzaylarının yanı sıra, Hilbert uzaylarına örnek olarak kare integrallenebilir fonksiyon uzayları, dizi uzayları, genelleştirilmiş fonksiyonlardan oluşan Sobolev uzayları ve holomorf fonksiyonların Hardy uzayları verilebilir.
Geometrik sezgi, Hilbert uzay teorisinin birçok yönünde önemli bir rol oynar. Pisagor teoreminin ve paralelkenar yasasının tam analogları bir Hilbert uzayında geçerlidir. Doğrusal bir alt uzaya dik izdüşüm, optimizasyon problemlerinde ve teorinin diğer yönlerinde önemli bir rol oynar. Bir Hilbert uzayının bir elemanı, klasik geometrideki Kartezyen koordinatlara benzer şekilde, bir dik tabana göre koordinatları tarafından biricik bir şekilde belirtilebilir. Bu taban sayılabilir derecede sonsuz olduğunda, Hilbert uzayının kare-toplanabilir sonsuz dizilerin uzayıyla özdeşleştirilmesine izin verir. Eski literatürde esas Hilbert uzayı bu ikinci uzay olarak bilinir.
Tanımı
[değiştir | kaynağı değiştir]Giriş
[değiştir | kaynağı değiştir]Hilbert uzayının en bilinen örneklerinden biri R3 ile gösterilen ve nokta çarpımı ile donatılmış üç boyutlu vektörlerden oluşan Öklid vektör uzayıdır. Nokta çarpımı iki vektör x ve y'yi alır ve x ⋅ y gerçel sayısını verir. Eğer x ve y Kartezyen koordinatlarda temsil edilirse, nokta çarpımı şu şekilde tanımlanır:
Nokta çarpımı şu özellikleri sağlar:
- x ve y için simetri (bakışım) özelliği vardır: x ⋅ y = y ⋅ x.
- Birinci değişkene göre doğrusaldır: Bütün a, b gerçel sayıları ve bütün x1, x2 ve y vektörleri için, (ax1 + bx2) ⋅ y = a(x1 ⋅ y) + b(x2 ⋅ y)
- Kesin pozitiftir: tüm x için, x ⋅ x ≥ 0 olur. 0'a eşitlik ise ancak ve ancak x = 0 olursa vardır.
Nokta çarpımı gibi bu üç özelliği sağlayan vektör çiftleri üzerindeki bir işlem (gerçel) iç çarpım olarak bilinir. Böyle bir iç çarpımla donatılmış bir vektör uzayı (gerçel) iç çarpım uzayı olarak bilinir. Her sonlu boyutlu iç çarpım uzayı aynı zamanda bir Hilbert uzayıdır. Nokta çarpımının onu Öklid geometrisine bağlayan temel özelliği, hem bir vektörün uzunluğu (veya normu) olan ||x||'e hem de iki vektör x ve y arasındaki açı olan θ ile aşağıdaki gösterilen bir ilişki içinde olmasıdır:
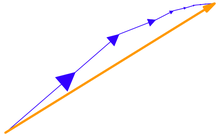
Öklit uzayları üzerinde yapılan vektör hesabı limitleri hesaplayabilme tekniklerine veya bu limitlerin varlığını göstermek için kullanılan kriterlere ihtiyaç duyar. R3'teki vektörler tarafından tanımlanmış bir seri, eğer bu vektörlerin uzunluklarının toplamı olan serisi bir gerçek sayı serisi olarak yakınsadığı takdirde kesinlikle yakınsaktır.[2]
Tıpkı bir sayı dizisi gibi, mutlak olarak yakınsayan bir vektör dizisi de Öklid uzayında L limit vektörüne yakınsar, yani
Bu özellik, Öklit uzayının tamlığını ifade eder : mutlak olarak yakınsayan bir seri, aynı zamanda olağan anlamda da yakınsar.
Hilbert uzayları genellikle karmaşık sayılar üzerinde alınır. C ile gösterilen karmaşık düzlemde büyüklük, karmaşık sayıların mutlak değeri |z| ile tanımlanır. Burada bir karmaşık sayı ile eşleniğinin çarpımı mutlak değerin karesini vermektedir: Eğer z karmaşık sayısı gerçel ve sanal kısmını gösterecek şekilde z = x + iy biçiminde yazılırsa, o zaman olur. İki karmaşık sayı z ve w'nin iç çarpımı z'nin w'nin karmaşık eşleniğiyle olan çarpımıdır: Bu çarpım karmaşık değerlidir. ⟨z, w⟩'nin gerçek kısmı, olağan iki boyutlu Öklid nokta çarpımını verir.
İkinci bir örnek, elemanları z = (z1, z2) karmaşık sayı çiftleri olan C2 uzayıdır. O zaman, z'nin w = (w1, w2) ile iç çarpımı olur.
⟨z, w⟩'nin gerçek kısmı o zaman iki boyutlu Öklit nokta çarpımıdır. Bu iç çarpım Hermit bakışımlıdır (simetriktir); yani, z ve w yer değiştirince elde edilen iç çarpım ilk iç çarpımın karmaşık eşleniğidir:
Tanım
[değiştir | kaynağı değiştir]Bir Hilbert uzayı, bir iç çarpım fonksiyonu tarafından oluşturulan uzaklık fonksiyonuna göre tam bir metrik uzay olan gerçek veya karmaşık bir iç çarpım uzayıdır.[3] Karmaşık bir vektör uzayı H'nin karmaşık bir iç çarpım uzayı olduğunu söylemek H'nin her elemanına karşılık gelen bir karmaşık sayıyı veren bir iç çarpım fonksiyonu 'nin varlığı analamına gelir.
- İç çarpım eşlenik simetriktir; yani, bir eleman çiftinin iç çarpımı, yer değiştiren elemanların iç çarpımının karmaşık eşlenik değerine eşittir: Dahası, bir gerçel sayıdır.
- İç çarpım ilk değişkende doğrusaldır: Herhangi bir ve karmaşık sayısı için,
- Bir elemanın kendisiyle iç çarpımı kesin pozitiftir.
1 ve 2 numaralı özelliklerden, karmaşık bir iç çarpımın ikinci değişkende antilineer, yani eşlenik doğrusal olduğu sonucu çıkar; bu da şu anlama gelir: Gerçel bir iç çarpım uzayı aynı şekilde tanımlanır; ancak, bu durumda, H gerçel bir vektör uzayıdır ve iç çarpım gerçel değerler alır. Böyle bir iç çarpım çifte doğrusal gönderim olacaktır ve bir eşiz (dual) sistem oluşturacaktır.[4]
Norm, gerçel değerli bir fonksiyondur: H'de yer alan elemenaları arasındaki uzaklık norm üzerinden tanımlanır:
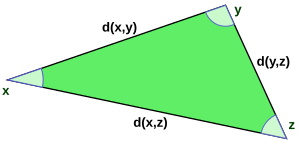
Bu fonksiyonun bir uzaklık fonksiyonu olması, öncelikle ve 'ye göre simetrik olduğu anlamına gelir. İkincisi, ile kendisi arasındaki uzaklık sıfırdır. Diğer durumda, ve 'e eşit olmayan bir arasındaki uzaklık pozitif olmalıdır. Son olarak, üçgen eşitsizliğinin geçerli olduğudur. Diğer deyişle, xyz üçgeninin bir kenarının uzunluğunun diğer iki kenarının uzunluklarının toplamını aşamayacağıdır:
Bu son özellik, Cauchy-Schwarz eşitsizliğinin bir sonucudur ve şunu ifade eder: Burada eşitlik ancak ve ancak ve doğrusal bağımlı ise olur.
Bu şekilde tanımlanan bir uzaklık fonksiyonu ile herhangi bir iç çarpım uzayı bir metrik uzaydır. Tam normlu bir uzay olarak Hilbert uzayları, tanım gereği Banach uzaylarıdır. Bu nedenle, alt kümelerin açıklığı ve kapalılığı gibi topolojik kavramların iyi tanımlandığı topolojik vektör uzaylarıdır. Önemli kavramlardan birisi Hilbert uzayının kapalı doğrusal alt uzayı kavramıdır. Eğer bir Hilbert uzayının kapalı bir altuzayında iç çarpım büyük uzaydaki iç çarpım sınırlandırılarak alınırsa, bu altuzay da tam bir metrik uzayın kapalı altuzayı olarak tam olur. Bu yüzden, Hilbert uzaylarının kapalı alt uzayları da kendi başlarına Hilbert uzayı olurlar.
Notlar
[değiştir | kaynağı değiştir]- ^ Moon, Todd K.; Stirling, Wynn (2000). Mathematical methods and algorithms for signal processing. Upper Saddle River, NJ: Prentice Hall. ISBN 0201361868.
- ^ Marsden 1974, §2.8
- ^ Bu bölümdeki matematik malzemesi bu konu hakkında yazılmış herhangi bir fonksiyonel analiz kitabında bulunabilir. Mesela, Dieudonné (1960), Hewitt & Stromberg (1965), Reed & Simon (1980) veya Rudin (1987) gibi.
- ^ Schaefer & Wolff 1999, ss. 122-202.
Kaynakça
[değiştir | kaynağı değiştir]- Dieudonné, Jean (1960), Foundations of Modern Analysis, Academic Press.
- Hewitt, Edwin; Stromberg, Karl (1965), Real and Abstract Analysis, New York: Springer-Verlag.
- Marsden, Jerrold E. (1974), Elementary classical analysis, W. H. Freeman and Co., MR 0357693.
- Reed, Michael; Simon, Barry (1980), Functional Analysis (vol I of 4 vols), Methods of Modern Mathematical Physics, Academic Press, ISBN 978-0-12-585050-6.
- Rudin, Walter (1987), Real and Complex Analysis, McGraw-Hill, ISBN 978-0-07-100276-9.
- Schaefer, Helmut H.; Wolff, Manfred P. (1999). Topological Vector Spaces. GTM. 8 (2 bas.). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.