Dalga (fizik)

Dalga (veya eski ifadesiyle mevce), bir fizik terimi olarak uzayda ve maddede yayılan ve enerjinin taşınmasına yol açan titreşime denir. Dalga hareketi, orta parçaların yer değişimi sıklıkla olmadan, yani çok az ya da hiç kütle taşınımı olmadan, enerjiyi bir yerden başka bir yere taşır. Dalgalar sabit konumlarda oluşan titreşimlerden oluşurlar ve zamanla nasıl ilerlediğini gösteren bir dalga denklemi ile tanımlanırlar. Bu denklemin matematiksel tanımı dalga çeşidine göre farklılık gösterir.
İki çeşit dalga vardır. Mekanik dalgalar bir ortam aracılığıyla yayılırlar ve deforme edilirler. Deformasyon ile kendini tersine çevirerek eski halindeki güçleri geri getirir. Mesela, ses dalgaları çarpışan hava molekülleri yolu ile yayılır. Hava molekülleri çarpıştığında, moleküller birbirleri boyunca sıçrarlar. Bu, moleküllerin dalganın yönünde yol almasını devam ettirir.
Dalgaların ikinci çeşidi elektromanyetik dalgalardır. Elektromanyetik dalgalar bir ortama ihtiyaç duymazlar. Bunun yerine yüklü parçacıklar tarafından, elektrik ve manyetik alanların periyodik titreşimlerinden meydana gelirler. Ve böylece boşlukta ilerlerler. Bu tip dalgaların ve radyo dalgalarının, mikrodalgaların, kızılötesi ışınların, görünür ışınların, morötesi ışınların, gama ışınlarının ve x ışınlarının dalga boyu değişir.
Ayrıca kuantum mekaniğinde parçacıkların davranışları dalgalar ile tanımlanır. Titreşimin yönüne bağlı olarak enine dalgalar ve boyuna dalgalar oluşabilir. Yayılmaya(enerji transferinin yönünde) dik sağ açılarda bir titreşim oluşursa enine dalgalar meydana gelir. Titreşimlerin yayılmanın yönüne paralel olduğu durumda ise boyuna dalgalar meydana gelir. Mekanik dalgalar enine ve boyuna olabilirken(ses dalgası sadece boyuna), bütün elektromanyetik dalgalar eninedir.
Genel özellikleri[değiştir | kaynağı değiştir]
Dalga terimi için hepsini kapsayan tek bir terim yoktur. Bir titreşim, bir referans değeri etrafındaki ileri-geri hareket olarak tanımlanabilir. Ama bir girişim, bir dalga olmak zorunda değildir. Mutlak bir olgu olarak tanımlayacak olursak, girişim, bir “dalga” nın belirsiz sınır çizgisindeki sonucudur.
Bir terim olarak “dalga” sıklıkla bir mekânsal bozulmanın taşınması ile ilgili olduğu anlaşılır. Bu mekânsal bozulma, hareket tarafından bir bütün olarak ortada tutulmaz. Bir dalgada titreşimin enerjisi bir karışıklık formunda kaynaktan çevrelediği ortam içerisinde uzaklaşır.[1] Ama bu hareket sabit dalga (mesela bir ipteki dalga) için sorunludur. Enerji nerede her yöne eşit olarak hareket ediyorsa, bu, dalganın algılanmasının ve pratik uygulamasının bir anahtarıdır. Aynı şekilde boşlukta hareket eden elektromanyetik dalgalar için (örnek olarak ışık), ortamın neresi olduğu önemli değildir ve bu da dalganın algılanmasının ve pratik uygulama yapılmasının bir anahtarıdır. Okyanus üzerindeki su dalgaları; güneş tarafından emilen gama dalgaları ve ışık dalgaları; mikrodalga fırınlarda kullanılan mikrodalgalar ve radar ekipmanları; radyo istasyonlarından yayılan radyo dalgaları ve radyo alıcılarından üretilen ses dalgaları, telefon ahizeleri sadece birkaç dalga türüdür.
Dalgaların tanımı, dalgaların fiziksel kökeni ile yakından ilgili gibi görünebilir. Mesela akustik optikten ayırt edilir. Bu ses dalgaları, titreşim sebebiyle oluşan elektromanyetik dalga transferine nazaran mekanik ile ilişkilendirilir. Bu nedenle akustik(optikten farklı olarak) dalga sürecinde kütle, momentum, eylemsizlik, ya da esneklik gibi kavramları tanımlamak zor hale gelir. Bu farklılık, herhangi bir dalganın belirli belirli karakteristik özelliklerini ortaya koyar. Mesela hava durumunda: girdap, radyasyon basıncı, şok dalgaları gibi; katıların durumunda ise: Rayleigh dalgaları, dağınıklık ve bunun gibi. Diğer özellikleri genellikle kökeni açısından tanımlanmasına rağmen, bütün dalga çeşitlerini genelleyebilir. Dalga teorisi her sebep için fizikin özel bir alanını simgeler.[2] Örneğin, uzayda ya da uzay-zamanda ilerleyen ve akustik dalgaların mekanik kökenine dayanan bir karışıklık sadece ne sonsuz esnek ne de sonsuz katı bir ortama sahip bir yerde varolabilir Eğer bir ortamda oluşturulan bütün parçalar katı bir şekilde “sınırlandırılmışsa” bunlar tek bir titreşim oluşturur. Titreşimin taşınmasında hiçbir gecikme olmaz ve bu nedenle de dalga hareketi olmaz. Diğer bir yandan, eğer bütün parçalar birbirinden bağımsız olursa titreşim taşınması yine oluşmaz ve dalga hareketi de olmaz. Yukarıdaki ifadeler, dalgaların bir ortama ihtiyaç duymasından bahsederken anlamsız olmasına rağmen, kökeni ne olursa olsun bütün dalgaların bir karakteristik özelliği olduğu açığa vurulur. Bir dalga için de, bitişik noktalar için titreşimin fazı (diğer bir deyişle, titreşim döngüsü içindeki konumu) farklıdır çünkü titreşim bu noktalara farklı zamanlarda ulaşır.
Benzer şekilde, ses dalgaları dışındaki dalgalarının üzerindeki çalışmalardan ortaya çıkan dalga süreci, ses olaylarının anlasılmasında önemli olabilir. İlgili bir örnek Thomas Young prensibidir.[3] Bu prensip ilk defa Young'ın ışık çalışmasında ve bâzı belirli bağlamlar içinde (mesela sesten sese saçılma) da kullanılmıştır. Bu prensip hala ses üzerindeki bir araştırma alanıdır
Tek boyutlu dalgaların matematiksel açıklaması[değiştir | kaynağı değiştir]
Dalga denklemi[değiştir | kaynağı değiştir]
Bir ipte ilerleyen enine dalga düşünün (titreşim gibi). Tek bir boyuta sahip ipi göz önünde bulundurun. Bu dalgayı ilerliyor olarak düşünün.
- yönünde. Mesela pozitif yönünü sağda, negatif yönünü solda kabul edelim.
- sabit genlikteki
- sabit hız, ve bu
- dalgaboyundan bağımsızdır
- genlikten bağımsızdır.[4]
• Sabit dalga yapısı ya da şekli vardır. O halde bu dalga iki boyutlu fonksiyonlar ile tanımlanabılır.
- (sağa doğru ilerleyen dalgası)
- (sola doğru ilerleyen dalgası)
Ya da genel olarak d'Alembert’in formülü olan:[5]
İki bileşeni ve olarak sembolize edilen dalgalar ters yönlere doğru ilerlerler. Bu dalganın genelleştirilmiş gösterimi kısmî differansiyel ile elde edilir.
Örnek bir türevi eq. (17) deki adımlarda görülebilir.[6]
Duhamel prensibine dayanan çözümler vardır.[7]
Dalga şekilleri[değiştir | kaynağı değiştir]

d'Alembert’in formülündeki F in şekli ya da formu x − vt konusunu içerir. Bu konunun sabit değerleri F in sabit değerlerine tekabül eder. Eğer x artarsa, aynı oranda vt artar böylece bu sabit değerler meydana gelir. Yani, dalga F fonksiyonu x yönünde ve v (ve G aynı hızda, negatif x yönünde üretir.) hızında ilerliyormuş gibi şekil alır.[8]
Periyodu λ olan bir periyodik F fonksiyonu, diğer bir deyişle F(x + λ − vt) = F(x − vt), F periyodunun anlamı verilen bir t zamanının anlık görüntüsü, λ (dalganın dalga boyu) periyodu ile bir alanda dalganın periyodik değişimi ile bulunur. Benzer şekilde, F in bu periyodu zamana bağlı bir periyod anlamına gelir: F(x − v(t + T)) = F(x − vt), vT = λ sağlanır. Böylece, sabit bir x noktasındaki dalganin gözlemi, T = λ/v periodu ile dalgalanan periodik dalga buldurur.[9]
Genlik ve geçiş[değiştir | kaynağı değiştir]

Bir dalganın genliği sabit olabilir (sürekli dalgalar) ya da zaman veya mekân değişiyorsa da geçiş dalgası olabilir. Genlikteki değişim n özeti, dalganın dalga paketinin genliği olarak da isimlendirilir. Matematiksel olarak geçiş yapan dalgaların gösterimi şöyledir:[10][11][12]
Burada dalganın paketinin genliği, dalga sayısı ve fazıdır. Eğer grup hızı (aşağıda) dalgaboyundan bağımsızsa, bu eşitlik şöyle gösterilebilir:[13]
Gösterilen paket, grup hızı ile hareket eder ve şeklini korur. Aksi takdirde, grup hızının dalga boyuyla değiştiği yerde, bir şekilde değişen titreşim şekli genellikle paket denklemi kullanılarak tarif edilir.[13][14]
Faz ve grup hızı[değiştir | kaynağı değiştir]

Dalgalarla ilgili olan iki çeşit hız vardır, faz hızı ve grup hızı. Bunları anlamak için önce dalgaların çeşitli türlerini düşünmek gerekir. Sadeleştirilirse inceleme tek boyutta sınırlanmıştır.

En temel dalga (dalga düzlemi formu) şu şekilde gösterilebilir:
Euler’in formülünü kullanarak genel sinüs ve kosinüs şekilleri ile ilişkili olan formül elde edilir. Bunu tekrar yazarsak, . Bir dalga boyunun titreşimi olan, x- yönünde sabit .[15] faz hızıyla ilerler.
Dalganın dikkate alınması gereken diğer türü bir paket tarafından açıklanan yerelleştirilmiş yapısıyla olan ifadedir. Matematiksel olarak mesela:
A(k1) (integral fourier dönüşümü olan A(k1) in tersidir.), k1 = k noktasını çevreleyen dalga vektörü Δk nın bölgesindeki net bir tepe sergileyen fonksiyondur. Üstel şekilde
Ao ile A nın büyüklüğü. Mesela Ao için yaygın bir seçim Gauss dalga paketidir.[16]
Σ, yaklaşık olarak k kadar olan k1 değerlerinin yayılmasını belirler ve N dalganın genliğidir.
Ψ için, üstel fonksiyonun içindeki integral hızla titreşir: φ(k1) ve hızla değiştiği yerde üsteller birbirini sıfırlar. ψ‘ye girişim yıkıcı bi şekilde, katkıda bulunmaksa azdır.[15] Fakat, yavaş değişen üstelin argument φ’sının olduğu yerde beklenir. (Bu gözlem, her integralin ölçümü için sabit faz methodunun temelidir.[17]) φ’nın yavaşça değişme şartı k1’in küçülme değişiminin oranıdır; bu değişimin oranı:[15]
k1 = k de yapılan ölçümde yapılır çünkü A(k1) burada merkezlenmiştir. Bu sonuç fazın yavaşça değiştiği, ψ’nin fark edilebilir olduğu yerdeki x’in konumunu gösterir. Böylece grup hız ile ilerlerler:
Bu sebeple grup hız dağılımı ilişkisi ω ve k ile bağlıdır. Örneğin, kuantum mekaniğinde, bir parçanın enerjisi E = ħω = (ħk)2/(2m) olan dalga paketiyle gösterilir. Sonuç olarak, bu dalga durumu için, grup hız
Quantum mekaniğinde localleştirilmiş bir parçanın hızı grup hız olarak gösterilir.[15] Çünkü grup hız k ile değişir. Dalga paketinin şekli zamanla genişler ve parça daha az localleşir.[18] Diğer bir deyişle, dalga paketinin meydana getiren dalgalarının hızı dalga boylarıyla orantılı değişerek ilerler. Böylece bazıları daha hızlı olur, bazılarıysa aynı girişim deseninde dalga düzeninde olarak kalamazlar.
Sinüs dalgaları[değiştir | kaynağı değiştir]

Matematiksel olarak, en temel dalga (uzaysal) tek boyutlu sinüs dalgalarıdır (ya da harmonik dalga). Genlikleri şöyle gösterilir:
- dalganın maksimum genliğidir. Bir ortam içindeki karışıklıktaki en yüksek nokta (tepe) ile bir dalga salınımının denge noktası arasındaki maksimum uzaklıktır. Ek olarak, bu, taban çizgisi ile dalga arasındaki maksimum dikey mesafedir.
- , koordinat alanıdır.
- , koordinat zamanıdır.
- , dalga sayısıdır.
- , açısal frekanstır.
- , faz sabitidir.
Genliğin birimi dalga çeşidine bağlıdır. Enine mekanik dalgaların (mesela bir ipteki dalgaların) genliği uzaklık ile ifade edilir (metre gibi). Boyuna mekanik dalgalar ise (mesela ses dalgaları) basınç birimlerini (pascal gibi) kullanır. Elektromanyetik dalgaların (enine vakum dalgaların formunda) genliği ise elektriksel alan açısından ifade edilir (volt/metre gibi).
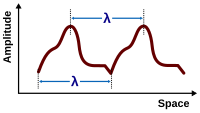
Dalga boyu , sıralı iki tepe ya da iki çukur (ya da diğer eşit noktalar) arasındaki uzaklıktır. Genellikle metre ile ölçülür. Dalga sayısı , dalganın radyan cinsinden her birim uzaklığının (genel olarak her metre) uzaysal frekansı, dalga boyu ile ilişkilendirilebilir.
Periyot , dalganın salınımının bir tam devir için geçen süresidir. Frekans , her bir zaman(her saniye) içindeki periyod sayısıdır ve genellikle hertz cinsinden ölçülür. Şöyle ilişkilendirilebilirler:
Diğer bir deyişle, dalganın frekansı ve periyodu karşıttır.
Açısal frekans saniye başına düşen radyan cinsinden frekansı simgeler. Frekans ya da pediyod birbiriyle şöyle bağıntıılır:
Sinüs dalga formunun dalgaboyu olan sabit bir hızında ilerleyen bağıntısı şudur:[19]
Dalganın faz hızı (faz hızının büyüklüğü) ve dalganın frekansı.
Sinüs fonksiyonu periyodiktir ve bu yüzden sinüs dalgaları, uzayda dalgaboyuna ve periyoda sahiptir.[20][21]
Sinüzoit bütün zaman ve uzaklıklar için tanımlanabilir. Fakat fiziksel durumlarda genellikle dalgaların zamanda sınırlı boşlukta yayılan ve duranlar için var olduğu zaman çözümleme yapılır. İyiki, keyfi dalga şeklisonsuz sinuzodial dalgalarda Fourier analizi ile ayrıştırılabilir. Böylece tek sinüzodial dalga çözümü daha genel olaylarda uygulanabilir.[22][23] Özellikle, birçok ortam doğrusal ya da neredeyse öyledir. Böylece keyfi dalga davranışlarının hesaplaması bireysel sinüs dalgalarını ekleyerek, süperpozisyon prensibini kullanarak bulunabilir.[24] Ortamın olmadığı yerde, kompleks dalgalara cevap sinüs-dalga ayrışması’ndan karar verilemez.
Düzlem dalgalar[değiştir | kaynağı değiştir]
Duran dalgalar[değiştir | kaynağı değiştir]

Ayrıca durağan dalga olarak da bilinen duran dalga sabit pozisyonda kalan bir dalgadır. Bu olay ortamın dalgaya zıt yönde hareket etmesi sonucunda meydana gelebilir ya da durağan bir ortamda zıt yönlerde hareket eden iki dalga arasındaki girişimin bir sonucu olarak ortaya çıkabilir
Bir birine karşı yayılan (eşit genlik ve frekansa sahip) iki dalganın toplamı, duran dalga oluşturur. Duran dalgalar genelde sınırın dalganın daha fazla yayılmasını engellemesi, böylece dalga yansımasına neden olması sonucunda ortaya çıkar ve dolayısıyla bir birine karşı yayılan dalga oluşturur. Örneğin bir keman teli yerinden oynatıldığında, enine dalgalar eşiğe, yayın yerinde durduğu yere ve topuğa, dalgaların geri yansıdığı yere yayılır. Eşik ve topukta iki ters dalga zıt evrededirler ve birbirini söndürerek düğüm oluştururlar. İki düğümün ortasında bir dalga karnı (antinode) oluşur, burada iki ters yönde yayılan dalga birbirini maksimum derecede arttırırlar. Zaman içinde enerjinin yayılımı yoktur.
-
Tek boyutlu duran dalgalar; temel frekans modu ve ilk beş armoniktir.
-
Bir disk üzerinde iki boyutlu bir duran dalga; bu temel moddur.
-
Merkezde kesişen iki düğüm hata sahip disk üzerinde bir duran dalga; bu bir armoniktir.
Fiziksel özellikler[değiştir | kaynağı değiştir]

Dalgalar bir standart durumda ortak davranış sergilerler, örnek:
İletim ve ortam[değiştir | kaynağı değiştir]
Dalgalar normalde bir iletim ortamı içinde düz bir çizgide hareket eder (yani doğrusal olarak). Bu gibi ortamlar aşağıdaki kategorilerden birine veya birkaç tanesine dahil olabilir:
- Sınırlı bir ortam , ortam sonlu ise, aksi takdirde sınırsız bir ortam
- Doğrusal bir orta ortam, içinde herhangi bir noktada, farklı dalgaların genlikleri eklenebiliyorsa
- Tekdüze veya homojen bir ortam, fiziksel özellikleri, uzayda farklı yerlerde aynı ise
- Anizotropik bir ortam, bir ya da daha fazla fiziksel özelliği bir ya da daha çok yönde değişiyorsa
- Izotropik bir ortam, fiziksel özellikleri her yönde aynı
Sönümlenme[değiştir | kaynağı değiştir]
Dalga sönümlenmesi, bir dalganın maddeye çarpası sonucunda, onun o madde tarafından sönümlenmesi anlamına gelir. Aynı doğal frekansa sahip bir dalga bir atoma çarparsa, bu atomun elektronları titreşim hareketine başlar. Belirli bir frekansa sahip dalga elektronların aynı titreşim frekanslarına sahip bir malzemeye çarpar ise, elektronlar dalga enerjisini emer ve onu titreşim hareketi dönüştürür.
Yansıma[değiştir | kaynağı değiştir]
Dalga yansıtıcı bir yüzeye çarptığı zaman yön değiştirir, dalga ile yüzey düzgeni arasında oluşan açı yansıyan dalga ile aynı düzgen arasındaki açıya eşittir. Dalga sönümlenmesi, bir dalganın maddeye çarpası sonucunda, onun o madde tarafından sönümlenmesi anlamına gelir. Aynı doğal frekansa sahip bir dalga bir atoma çarparsa, bu atomun elektronları titreşim hareketine başlar. Belirli bir frekansa sahip dalga elektronların aynı titreşim frekanslarına sahip bir malzemeye çarpar ise, elektronlar dalga enerjisini emer ve onu titreşim hareketi dönüştürür.
Girişim[değiştir | kaynağı değiştir]
Birbirleriyle çarpışan dalgalar girişim örüntüsü olarak adlandırılan yeni bir dalga yaratmak için süperpozisyon ile birleştirir. Önemli girişim örüntüleri eşevreli (eşfazlı) dalgalar için ortaya çıkar.
Kırılma[değiştir | kaynağı değiştir]
Titreyen tel boyunca hareket eden enine dalganın hızı ( v ), telin geriliminin ( T ) çizgisel kütle yoğunluğuna ( μ ) oranının kare köküyle düz orantılıdır.
burada çizgisel yoğunluk μ, telin birim uzunluğu başına kütle olduğudur.
Akustik dalgalar[değiştir | kaynağı değiştir]
Akustik veya ses dalgaları aşağıdaki hızla hareket ederler:
ya da adiyabatik hacimsel basınç katsayısının ortam akışkan yoğunluğuna oranının kare kökü (Sesin hızına bakınız).
Su dalgaları[değiştir | kaynağı değiştir]

- Bir göletin yüzeyinde oluşan çember şeklinde dalgacıklar aslında enine ve boyuna dalgaların bir arada olduğu durumdur, bu nedenle yüzeydeki noktalar çevresel yörünge yolları izler
- Ses – bir mekanik dalga gaz, sıvı, katı ve plazmalar yoluyla yayilir;
- Eylemsiz dalgalar Döner sıvılarda ortaya çıkar ve Coriolis etkisi ile onarılır;
- Okyanus yüzeyindeki dalgalar su yoluyla yayılan pertübasyonlardır.
Sismik dalgalar[değiştir | kaynağı değiştir]
Şok dalgaları[değiştir | kaynağı değiştir]

Diğer[değiştir | kaynağı değiştir]
- Trafik dalgaları, yani farklı yoğunluklarda motorlu araçların sahipolduğu kinematik dalgalar olarak modellellenebilir.[25]
- Metakronal dalga koordine edilmiş ardışık eylemler tarafından oluşturulan, yayılan dalgaların ortaya çıkmasını tanımlar.
- Belirtmek gerekiyor ki, bu şekil için kütle-enerji denkliği aşağıdaki şekilde çözülebilir: .
Elektromanyetik dalgalar[değiştir | kaynağı değiştir]
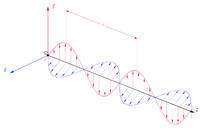
Bir elektromanyetik dalga, elektrik ve manyetik alanların salınımlarından olan iki dalga oluşur. Bir elektromanyetik dalga her iki alanın da salınım doğrultusuna dik açıya sahip bir yönde hareket eder. 19. yüzyılda, James Clerk Maxwell vakumda, hem elektrik ve hem de manyetik alanların ışık hızına eşit bir hızda yayılması durumunda denklemin sağlandığını göstermiştir. Bu nedenle ışık bir elektromanyetik dalga olduğu fikri ortaya çıktı. Elektromanyetik dalgalar farklı frekanslar (ve dolayısıyla dalga boylarına) sahip olabilir, bu nedenle radyo dalgaları, mikrodalgalar, kızılötesi, görünür ışık, ultraviyole ve X-ışınları gibi farklı ışınım şeklinde olabilirler.
Kuantum mekaniği dalgaları[değiştir | kaynağı değiştir]
Schrödinger denklemi, dalgaları kuantum mekaniğindeki parçacıkların davranışları gibi açıklar. Bu eşitliğin çözümü bir parçacığın kullanılabilme olasılığının dalga fonksiyonudur.

de Broglie dalgaları[değiştir | kaynağı değiştir]
Louis de Broglie bütün parçaların momentum ile birlikte dalga boyunada sahip olduğunu doğru kabul eder.
h Planck sabiti ve, p parçanın momentum büyüklüğüdür Bu hipotez kuantum mekaniğinin temelidir. Günümüzde bu dalga boyu, de Broglie dalgaboyu olarak adlandırılır. Örneğin, bir CRT içinde elektron lar ın de Broglie dalga boyu yaklaşık 10−13 metredir. K yönünde ilerleyen bir dalga, dalga denklemi ile aşağıdaki gibi gösterilir:
Dalga boyu, dalga vektörü olan] k ile:
Ve momentum:
Ancak, böyle belirli bir dalga boyu olan bir dalga, bir alanda sınırlandırılamaz. Bu yüzden bir dalga bir alanla sınırlandırılmış olarak gösterilemez. Bir parçacığın yerini belirlemek için de Broglie, bir dalga yığınında, farklı dalga boylarının çakışmasının bir orta değer etrafında değiştiğini ileri sürmüştür.[27] bir dalga yapısı, bir parçacığın dalga fonksiyonunu tanımlamak için kuantum mekaniğinde sıklıkla kullanılır. Bir dalga yığınında dalga boyu kesin değildir ve yerel dalga boyu, ana dalga boyu değerinin her iki tarafında da sapma sergiler Yerelleştirilmiş bir parçacığın dalga fonksiyonunun gösterimi şöyle olur: bir dalga yığını Gauss şeklini alır ve Gauss dalga yığını olarak adlandırılır.[28] Gauss dalga yığını, su dalgalarını çözümlemek için de kullanılır.[29]
Mesela bir Gauss dalga denkleminde ψ şöyle olabilir:[30]
t = 0 olduğu bir başlangıç zamanında, merkezi dalga boyu, merkezi dalga vektörü olan k0, λ0 = 2π / k0 ile bağlantılıdır. Bunun Fourier analiz,[31] ya da Heisenberg belirsizlik prensibinden geldiği bilinir. Gauss dalgasının Fourier dönüşümü kendisidir.[32] Verilen Gauss dalgası
Fourier dönüşümü:
Bu yüzden Gauss dalgası bir alanda dalga oluşturur:
dalga boyu sayısı λ olan dalgaların sayısı kλ = 2 π.
Fourier dönüşümü, 1/σ tarafından belirlenen k dalga vektörnün yayılmasını gösterirken, σ parametresi, Gaussun x- ekseni boyunca yayılmasına karar verir.

Kütleçekimsel dalga[değiştir | kaynağı değiştir]
Kütleçekimsel dalgaların doğrudan algılanamamasına rağmen araştırmacılar, kütleçekimsel dalgaların uzayın içinden ilerlediğine inanıyorlar.
Kütleçekimsel dalgaların uzayzamanın eğriliğnde, Einstein'ın genel görelilik kuramı tarafından öngörülen bozukluklar vardır. Bu Yerçekimi dalgaları ile karıştırılmamalıdır
WKB metodu[değiştir | kaynağı değiştir]
Dalga sayısı, k, konuma ve frekansa bağlıdır ve standart olmayan bir ortamda faz terimi WKB metoduna göre kx genellikle k ( x) dx integrali ile yer değişir. Böyle standart olmayarak ilerleyen dalgalar fizik problemlerinde çok yaygındır. Asılı iplerdeki dalga ve cochlea ların mekaniğinde de kullanılır.
Kaynakça[değiştir | kaynağı değiştir]
- ^ Hall 1980, s. 8
- ^ Lev A. Ostrovsky & Alexander I. Potapov (2002). Modulated waves: theory and application. Johns Hopkins University Press. ISBN 0-8018-7325-8. 16 Mart 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Haziran 2014.
- ^ Young, 1802, in Şablon:Harvard alıntınb
- ^ Michael A. Slawinski (2003). "Wave equations". Seismic waves and rays in elastic media. Elsevier. ss. 131 ff. ISBN 0-08-043930-6.
- ^ Karl F Graaf (1991). Wave motion in elastic solids (Reprint of Oxford 1975 bas.). Dover. ss. 13-14. ISBN 978-0-486-66745-4.
- ^ Francis Redfern. "Kinematic Derivation of the Wave Equation". Physics Journal. 24 Temmuz 2013 tarihinde kaynağından arşivlendi. Erişim tarihi: 20 Mart 2016.
- ^ Jalal M. Ihsan Shatah, Michael Struwe (2000). "The linear wave equation". Geometric wave equations. American Mathematical Society Bookstore. ss. 37 ff. ISBN 0-8218-2749-9.
- ^ Louis Lyons (1998). All you wanted to know about mathematics but were afraid to ask. Cambridge University Press. ss. 128 ff. ISBN 0-521-43601-X.
- ^ Alexander McPherson (2009). "Waves and their properties". Introduction to Macromolecular Crystallography (2 bas.). Wiley. s. 77. ISBN 0-470-18590-2.
- ^ Christian Jirauschek (2005). FEW-cycle Laser Dynamics and Carrier-envelope Phase Detection. Cuvillier Verlag. s. 9. ISBN 3-86537-419-0.
- ^ Fritz Kurt Kneubühl (1997). Oscillations and waves. Springer. s. 365. ISBN 3-540-62001-X.
- ^ Mark Lundstrom (2000). Fundamentals of carrier transport. Cambridge University Press. s. 33. ISBN 0-521-63134-3.[ölü/kırık bağlantı]
- ^ a b Chin-Lin Chen (2006). "§13.7.3 Pulse envelope in nondispersive media". Foundations for guided-wave optics. Wiley. s. 363. ISBN 0-471-75687-3.
- ^ Stefano Longhi, Davide Janner (2008). "Localization and Wannier wave packets in photonic crystals". Hugo E. Hernández-Figueroa, Michel Zamboni-Rached, Erasmo Recami (Ed.). Localized Waves. Wiley-Interscience. s. 329. ISBN 0-470-10885-1.
- ^ a b c d Albert Messiah (1999). Quantum Mechanics (Reprint of two-volume Wiley 1958 bas.). Courier Dover. ss. 50-52. ISBN 978-0-486-40924-5.
- ^ Walter Greiner, D. Allan Bromley (2007). Quantum Mechanics: An introduction (2.2 yayıncı = Springer bas.). ss. 60-61. ISBN 3-540-67458-6.
- ^ John W. Negele, Henri Orland (1998). Quantum many-particle systems (Reprint in Advanced Book Classics bas.). Westview Press. s. 121. ISBN 0-7382-0052-2.[ölü/kırık bağlantı]
- ^ Donald D. Fitts (1999). Principles of quantum mechanics: as applied to chemistry and chemical physics. Cambridge University Press. ss. 15 ff. ISBN 0-521-65841-1.[ölü/kırık bağlantı]
- ^ David C. Cassidy, Gerald James Holton, Floyd James Rutherford (2002). Understanding physics. Birkhäuser. ss. 339 ff. ISBN 0-387-98756-8.
- ^ Aleksandr Tikhonovich Filippov (2000). The versatile soliton. Springer. s. 106. ISBN 0-8176-3635-8.
- ^ Seth Stein, Michael E. Wysession (2003). An introduction to seismology, earthquakes, and earth structure. Wiley-Blackwell. s. 31. ISBN 0-86542-078-5.
- ^ Seth Stein, Michael E. Wysession (2003). op. cit.. s. 32. ISBN 0-86542-078-5.
- ^ Kimball A. Milton, Julian Seymour Schwinger (2006). Electromagnetic Radiation: Variational Methods, Waveguides and Accelerators. Springer. s. 16. ISBN 3-540-29304-3.
Thus, an arbitrary function f(r, t) can be synthesized by a proper superposition of the functions exp[i (k•r−ωt)]...
- ^ Raymond A. Serway and John W. Jewett (2005). "§14.1 The Principle of Superposition". Principles of physics (4.4 yayıncı = Cengage Learning bas.). s. 433. ISBN 0-534-49143-X.
- ^ M. J. Lighthill; G. B. Whitham (1955). "On kinematic waves. II. A theory of traffic flow on long crowded roads". Proceedings of the Royal Society of London. Series A. Cilt 229. ss. 281-345. Bibcode:1955RSPSA.229..281L. doi:10.1098/rspa.1955.0088. And: P. I. Richards (1956). "Shockwaves on the highway". Operations Research. 4 (1). ss. 42-51. doi:10.1287/opre.4.1.42.
- ^ A. T. Fromhold (1991). "Wave packet solutions". Quantum Mechanics for Applied Physics and Engineering (Reprint of Academic Press 1981 bas.). Courier Dover Publications. ss. 59 ff. ISBN 0-486-66741-3.
(p. 61)...bireysel dalgalar paketlerden daha yavaştır ve bu yüzden o ilerledikçe paket üzerinden geri dönerler.
- ^ Ming Chiang Li (1980). "Electron Interference". L. Marton & Claire Marton (Ed.). Advances in Electronics and Electron Physics. 53. Academic Press. s. 271. ISBN 0-12-014653-3.
- ^ Walter Greiner, D. Allan Bromley (2007). Quantum Mechanics (2 bas.). Springer. s. 60. ISBN 3-540-67458-6. and John Joseph Gilman (2003). Electronic basis of the strength of materials. Cambridge University Press. s. 57. ISBN 0-521-62005-8.[ölü/kırık bağlantı], Donald D. Fitts (1999). Principles of quantum mechanics. Cambridge University Press. s. 17. ISBN 0-521-65841-1.[ölü/kırık bağlantı].
- ^ Chiang C. Mei (1989). The applied dynamics of ocean surface waves (2.2 yayıncı = World Scientific bas.). s. 47. ISBN 9971-5-0789-7.
- ^ Walter Greiner, D. Allan Bromley. Quantum Mechanics (2.2 yıl = 2007 bas.). Springer. s. 60. ISBN 3-540-67458-6.
- ^ teorisinden Siegmund Brandt, Hans Dieter Dahmen (2001). The picture book of quantum mechanics (3.3 yayıncı = Springer bas.). s. 23. ISBN 0-387-95141-5.
- ^ Cyrus D. Cantrell (2000). Modern mathematical methods for physicists and engineers. Cambridge University Press. s. 677. ISBN 0-521-59827-3.
Literatür[değiştir | kaynağı değiştir]
- Campbell, M. and Greated, C. (1987). The Musician’s Guide to Acoustics. New York: Schirmer Books.
- French, A.P. (1971). Vibrations and Waves (M.I.T. Introductory physics series). Nelson Thornes. ISBN 0-393-09936-9. OCLC 163810889.
- Hall, D. E. (1980). Musical Acoustics: An Introduction. Belmont, California: Wadsworth Publishing Company. ISBN 0-534-00758-9..
- Hunt, F. V. (1992) [1966]. "Origins in Acoustics". New York: Acoustical Society of America Press. 27 Şubat 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Haziran 2014..
- Ostrovsky, L. A.; Potapov, A. S. (1999). Modulated Waves, Theory and Applications. Baltimore: The Johns Hopkins University Press. ISBN 0-8018-5870-4..
- Vassilakis, P.N. (2001) 27 Ekim 2013 tarihinde Wayback Machine sitesinde arşivlendi.. Perceptual and Physical Properties of Amplitude Fluctuation and their Musical Significance. Doctoral Dissertation. University of California, Los Angeles.
Ayrıca bakınız[değiştir | kaynağı değiştir]
Dış bağlantılar[değiştir | kaynağı değiştir]
| Wikimedia Commons'ta Wave ile ilgili ortam dosyaları bulunmaktadır. |
| Vikisözlük'te dalga (fizik) ile ilgili tanım bulabilirsiniz. |
- Interactive Visual Representation of Waves10 Ocak 2008 tarihinde Wayback Machine sitesinde arşivlendi.
- Science Aid: Wave properties—Concise guide aimed at teens11 Kasım 2006 tarihinde Wayback Machine sitesinde arşivlendi.
- Simulation of diffraction of water wave passing through a gap4 Aralık 2009 tarihinde Wayback Machine sitesinde arşivlendi.
- Simulation of interference of water waves24 Ocak 2007 tarihinde Wayback Machine sitesinde arşivlendi.
- Simulation of longitudinal traveling wave24 Şubat 2007 tarihinde Wayback Machine sitesinde arşivlendi.
- Simulation of stationary wave on a string27 Mart 2008 tarihinde Wayback Machine sitesinde arşivlendi.
- Simulation of transverse traveling wave 9 Ekim 2014 tarihinde Wayback Machine sitesinde arşivlendi.
- Sounds Amazing—AS and A-Level learning resource for sound and waves 17 Haziran 2014 tarihinde Wayback Machine sitesinde arşivlendi.
- chapter from an online textbook 10 Temmuz 2014 tarihinde Wayback Machine sitesinde arşivlendi.
- Simulation of waves on a string
- of longitudinal and transverse mechanical wave15 Mayıs 2016 tarihinde Portuguese Web Archive sitesinde arşivlendi
- MIT OpenCourseWare 8.03: Vibrations and Waves7 Kasım 2010 tarihinde Library of Congress sitesinde arşivlendi Free, independent study course with video lectures, assignments, lecture notes and exams.


















































