Elektrik alanı
| Elektromanyetizma |
|---|
 |
Elektriksel alan, kıvıl alan, elektrik alan veya elektrik alanı, elektriksel yükü veya manyetik alanı çevreleyen uzayın bir özelliği olup, içerisinde bulunan yüklü nesnelere elektriksel güç aracılığı ile etki eder. Kavram fiziğe Michael Faraday tarafından kazandırılmıştır.
Elektrik alanı SI birimi Newton/Coulomb ya da Volt/metre olan bir vektör alanıdır. SI temel birimleri cinsinden kg·m·s−3·A−1 olarak ifade edilir. Alanın belli bir noktadaki büyüklüğü o noktaya konacak 1 Coulomb'luk bir test yüküne ne kadar kuvvet uygulayacağıyla belirlenir, alanın yönü kuvvetin yönüdür. Elektrik alan, yoğunluğunun büyüklüğü alan büyüklüğünün karesiyle doğru orantılı elektriksel enerjiye sahiptir. Elektrik alanın yükle ilişkisi yerçekimi ivmesinin kütleyle ilişkisinin ve kuvvet yoğunluğunun hacimle ilişkisi gibidir.
Zamana göre değişen bir elektrik alanı (mesela hareketli bir yüklü parçacık nedeniyle) yerel manyetik alana sebep olur. Bu, elektrik ve manyetik alanların birbirinden bağımsız olmadığını gösterir; bir gözlemcinin yalnızca elektrik alanı olarak gözlemlediğini başka bir referansa göre başka bir gözlemci bir elektrik ve manyetik alan karışımı olarak gözlemleyebilir. Bu nedenle elektrik ve manyetik alanlardan ayrı ayrı bahsetmek yerine bu ikisi “elektromanyetizma” ya da “elektromanyetik alan” olarak, birlikte incelenir. Kuantum mekaniğinde elektromanyetik alandaki değişmeler foton olarak adlandırılır ve fotonun enerjisi kuantize olmuştur.
Tanım
[değiştir | kaynağı değiştir]Elektrik alanı, uzay içinde belli bir noktada sabit duran noktasal yüke uygulanan, yük başına düşen kuvvet olarak tanımlanır:
F parçacık tarafından hissedilen elektriksel kuvvet, q parçacığın yükü, E parçacığın konumundaki elektrik alan.
Bu denklem elektrik alanı yalnızca alanda durağan yükler olduğunda tanımlar. Dahası, alandaki yükler elektrik alanı değiştireceğinden, herhangi bir q yükünün varlığındaki elektrik alanı o yük olmadığında olandan daha farklı olacaktır. Fakat, verili bir yük dağılımından kaynaklanan elektrik alanı bu alanı hissedecek hiçbir parçacık olmasa dahi tanımlıdır. Bu tanımlılık alana varsayımsal olarak yerleştirilen test yükü ile sağlanır. Bu sayede elektrik alanı test yükü sıfıra yaklaşırken yükün hissedeceği kuvvet ile tanımlanır:
Bu ifade elektrik alanın yalnızca kaynak yük dağılımına bağlı olmasını sağlar.
Tanımdan anlaşılabilceği üzere elektrik alanın yönü pozitif yüklü parçacığın hissedeceği kuvvetin yönüyle aynı, negatif yüklü parçacığın hissedeceği kuvvetin yönünün zıddıdır. Aynı yükler birbirini itip zıt yükler birbirini çekeceğinden (aşağıda formülü verilmiştir), pozitif yüklerin etrafındaki alanların dışarıyı gösterdiğini ve negatif yüklerin etrafındaki alanların içeriye doğru yöneldiğini söyleyebiliriz.
Coulomb yasasına dayanarak, uzayda tek bir noktasal yük tarafından üretilen elektrik alanı yazabiliriz: E=1/4pi... q elektrik alanı üreten parçacığın yükü, r elektrik alanı hesapladığımız nokta ile q yükü arasındaki uzaklık, r q yükünden elektrik alanın hesaplandığı noktayı gösteren birim vektör, epsilon yalıtkanlık sabiti.
Birden fazla noktasal yükün ürettiği elektrik alanı yüklerin teker teker ürettiği elektrik alanların süperpozisyonudur:
Alternatif olarak, Gauss yasası uzayda sürekli bir yük yoğunluğu dağılımının ürettiği elektrik alanı hesaplamamızı sağlar.
ρ pozisyona bağlı olarak yük yoğunluğunu verir.
Coulomb yasası esasen elektrik yük dağılımı ile bu dağılımdan kaynaklanan elektrik alanı arasındaki ilişkiyi gösteren Gauss yasasının özel bir halidir. Gauss yasası elektromanyetik teoriyi oluşturan dört Maxwell denklemlerinden biridir.
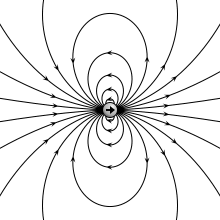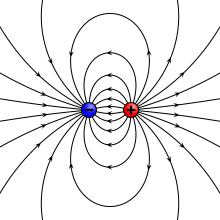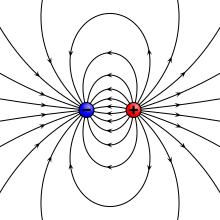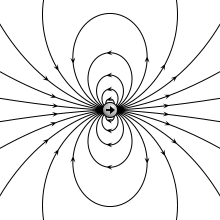
Elektrik alanı çizgileri
[değiştir | kaynağı değiştir]Elektrik alanını zihinde daha kolay canlandırmak için elektrik alanı çizgileri kullanılır. Elektrik alanı çizgilerinin özellikleri şunlardır:
- E elektrik alanı vektörü, elektrik alanı çizgisine her noktada teğettir.
- Alan çizgileri birbirine yakın olduğunda E büyük, uzak olduğunda küçüktür.
- Alan çizgileri bir artı yükten çıkıp bir eksi yükte son bulmalıdır.
- Alan çizgilerinin sayısı yük miktarıyla orantılıdır.
- İki alan çizgisi birbirini kesmez.

Sabit alanlar
[değiştir | kaynağı değiştir]Her noktada aynı değere sahip olan elektrik alana sabit elektrik alanı denir.İki paralalel iletken levhaya potansiyel fark uygulanarak yaklaşık olarak elde edilebilir.Yaklaşık olmasanın sebebi elektrik alanın köşelerde düzenli halinden uzaklaşmasıdır.Bu etkenleri ihmal edersek eşitlik
halini alır.
- U levhalar arası potansiyel fark
- d levhalar arası uzaklık
Bu eşitlik sadece elektrik alanın büyüklüğünü vermektedir.Elektrik alanın yönü ise pozitif yüklü levhada negatif yüklü levhaya doğrudur.

Sabit alanda yüklü parçacığın hareketi
[değiştir | kaynağı değiştir]m kütleli, q yüklü bir cismi E elektrik alanına koyarsak, bu cisme kadarlık bir net kuvvet etki eder, dolayısıyla cisim ivmeli hareket yapar. (Newton'ın hareket yasaları) Yani cismin ivmesi
Zamana bağlı alanlar
[değiştir | kaynağı değiştir]Elektrik alanı durağan bir yük tarafından üretilebileceği gibi değişen manyetik alanın sonucu olarak da oluşurlar. Sonuç olarak,
phi skaler elektrik potansiyeli, A manyetik vektör potansiyeli.
Aynı zamanda vektörü manyetik debi yoğunluğunu verir. Elektrik alanı denkleminin curl'ünü alırsak,
Bu denklem Maxwell denklemlerinden biridir, Faraday-Lenz yasası olarak bilinir.
Elektrostatik durağan yükleri çevreleyen elektrik alanların bilimiyken manyetik alanın değişmesiyle oluşan elektrik alanlar elektrodinamik ve elektromanyetik konusudur.
Elektrostatik özellikler
[değiştir | kaynağı değiştir]Yukarıdaki denklemlerde görüldüğü gibi elektrik alanı pozisyona bağlıdır. Noktasal bir yük tarafından üretilen elektrik alanı parçacığa olan uzaklığın karesiyle azalır.
Elektrik alanı süperpozisyon prensibine uyar. Eğer birden fazla noktasal kaynak varsa herhangi bir noktadaki toplam elektrik alanı bu noktasal kaynakların o noktada tek başına ürettiği elektrik alanların vektörel toplamıdır.
Bu kural sonsuz sayıda küçük yük elementi için genişletilirse toplam formülü integrale dönüşür:
ρ pozisyona bağlı olarak yük yoğunluğunu yani birim hacme düşen yük miktarını verir.
Bir noktadaki elektrik alanı o noktadaki elektriksel potansiyelin negatif gradyanına eşittir:
φ verilen noktada elektriksel potansiyeli gösteren skaler alandır.
Eğer birden fazla yük dağılımını böyle bir elektriksel potansiyel üretiyorsa (örneğin bir katıda) elektrik alanı gradyanı da tanımlanabilir.
Doğrusal materyallerin yalıtkanlık sabiti epsilon olmak üzere, dielektrik alan aşağıdaki formül ile verilir:
Elektriksel potansiyel enerji
[değiştir | kaynağı değiştir]Elektrik alanı enerji depolar. Bir elektrik alanın enerji yoğunluğu aşağıdaki gibidir.
epsilon alanın içerisinde bulunduğu yerin yalıtkanlık sabiti, E elektrik alanı vektörüdür. Böylece, verili bir V hacminde depolanan toplam enerji dV diferansiyel hacim elementi olmak üzere
olarak verilir.
Elektrostatik ve kütleçekimi arasındaki paralellikler
Elektrik yükleri arasındaki ilişkiyi gösteren Coulomb yasası
Newton'ın evrensel kütleçekim yasası ile benzerdir:
Bu, elektrik alanla yer çekimi alanı arasında benzerlikler olduğunu gösterir. Bu benzerlikler:
- İkisi de boşlukta yayılır.
- İkisi de merkezidir ve korunur.
- İkisi de ters kare yasasına uyar.
- İkisi de ışık hızıyla yayılır.
- Elektrik yükü ve relativistik kütle korunur. (Not: Buna karşın durağan kütle korunmaz.)
Elektrostatik ve kütleçekim kuvvetleri arasındaki farklar:
- Elektrostatik kuvvet kütleçekim kuvvetinden çok daha fazla kuvvetlidir (yaklaşık 1036 kat).
- Kütleçekiminde benzer yüklerin birbirini itmesi söz konusu değildir.
- Negatif yüklerin var olmasına karşın negatif kütle diye bir şey yoktur. Bu madde bir öncekiyle birleştirildiğinde, kütleçekim kuvvetinde kütlelerin birbirini her zaman çektiğini fakat elektrostatik kuvvetlerde yüklerin birbirini hem çekip hem itebildiklerini söyleyebiliriz.
Kaynakça
[değiştir | kaynağı değiştir]Dış bağlantılar
[değiştir | kaynağı değiştir]- [1] 28 Nisan 2010 tarihinde Wayback Machine sitesinde arşivlendi. - Hareket eden noktasal bir parçacığın elektrik alanını gösteren bir uygulama.
- Fields 27 Mayıs 2010 tarihinde Wayback Machine sitesinde arşivlendi. - Online bir kitaptan parça (İngilizce).
- Learning by Simulations 4 Temmuz 2010 tarihinde Wayback Machine sitesinde arşivlendi. - Dört noktasal parçacığa kadar elektrik alanı gösteren interaktif bir uygulama.
- electrostatics in 2-D 15 Kasım 2010 tarihinde Wayback Machine sitesinde arşivlendi. ve 3-D 15 Kasım 2010 tarihinde Wayback Machine sitesinde arşivlendi. - Java simülasyonları.
- Electric Fields Applet 4 Aralık 2010 tarihinde Wayback Machine sitesinde arşivlendi. - Elektrik alanı ve potansiyel gradyanları gösteren bir uygulama.
- The inverse cube law 22 Kasım 2009 tarihinde Wayback Machine sitesinde arşivlendi. Dipoller için ters küp yasası (PDF formatında, İngilizce)


















