Fourier dönüşümü
Fourier dönüşümü, fizik, mühendislik ve matematikte, bir fonksiyonu, içerdiği frekansların belirtildiği bir biçime dönüştüren bir integral dönüşümüdür. Dönüşümün çıktısı, frekansa bağlı karmaşık değerli bir fonksiyondur. "Fourier dönüşümü" terimi, hem bu karmaşık değerli fonksiyon için hem de buna karşılık gelen matematiksel operasyon için kullanılmaktadır. Bu ayrımın netleştirilmesi gerektiğinde, Fourier dönüşümü bazen orijinal fonksiyonun frekans uzayında temsili olarak adlandırılır. Fourier dönüşümü, bir müzik akorunun sesini, onu oluşturan tonlara ayrıştırmaya benzer.[1]
Fourier dönüşümü, sürekli ve ayrık olarak ikiye ayrılabilir. İki dönüşüm de bir nesneyi ortogonal iki uzay arasında eşler. Sürekli nesneler için dönüşüm:
- ve
şeklinde verilir. Yukarıdaki dönüşümde görüleceği üzere x uzayındaki bir nesne k uzayında tanımlanmıştır. Bu dönüşüm diferansiyel denklemlerin çözümünde çok büyük rahatlık sağlar zira bu dönüşüm sayesinde x uzayındaki diferansiyel denklemler k uzayında lineer denklemler olarak ifade edilirler. K uzayında bu denklemin çözümü bulunduktan sonra ters dönüşümle x uzayındaki karşılığı elde edilir, ki bu diferansiyel denklemin çözümüdür. Birinci dönüşümdeki ifade ikinci dönüşümde yerine oturtularak,
- ,
ifadesine ulaşılır. Parantez içindeki ifadenin olduğu görülebilir. Anlaşıldığı üzere eşlemesine Fourier Dönüşümü, eşlemesine de Ters Fourier Dönüşümü denir ve bu eşlemeler (mapping) yapılırken baş harfleri büyük yazılarak gösterilir (FD ve TFD). Parantez içindeki ifadenin Delta fonksiyonunun temsili olması ise açıkça bir düz ve bir ters Fourier dönüşümü yapılan bir ifadenin kendine eşit olmasından kaynaklanır. Dönüşüm uzayları keyfi seçilebilir ancak fizikte, konum uzayından momentum uzayına ve zaman uzayından enerji uzayına De Broglie-Einstein denklemleriyle geçişler tanımlanmıştır.
Giriş
[değiştir | kaynağı değiştir]Örnek
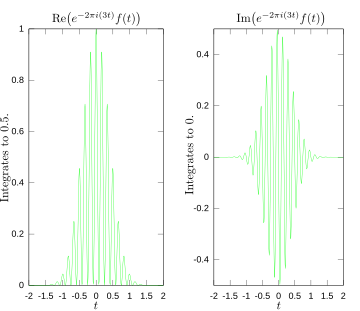
[değiştir | kaynağı değiştir]Aşağıdaki görüntülerde Fourier dönüşümünün veren bir görsel ilüstrasyon sağlama ölçümü olan bir frekans bir özel fonksiyon içinde mevcuttur. Fonksiyon f(t) = cos(6πt) e−πt2 3 hertz'te salınım göstermektedir (eğer t ölçüsü saniyeler ise) ve 0 a doğru hızla gitme eğilimdedir. (bu denklem içinde saniye faktörü bir zarf fonksiyonu ve bir kısa vuruş içinde sürekli sinüzoidal şekillerdir. Bunun genel formu bir Gauss fonksiyonudur). Bu fonksiyon özel seçilmiş idi var olan bir gerçek Fourier dönüşümü için kolayca çizilebilir. İlk görüntü bu grafı içerir. hesaplamak için sırayla e−2πi(3t)f(t) integrali olmalıdır. İkinci görüntü bu fonksiyonun gerçel ve sanal kısımlarını gösterir. İntegrand'ın gerçel kısmı hemen hemen her zaman pozitif, çünkü eğer f(t) negatif ise, e−2πi(3t)'nin gerçek kısmı da negatiftir. Çünkü bu aynı kesirde salınıyorsa eğer f(t) pozitif ise, böylece e−2πi(3t)'nin gerçel kısmıdır. Sonuç olarak eğer integrandın gerçek kısım integrali ise bir göreceli büyük sayı alıyorsunuz (0.5 durumu içinde). Diğer taraftan, eğer bir frekans ölçüsü için deniyorsanız bu mevcut değildir, da gördüğümüz durumu içindeki gibi yeterince salınan integrand gibi integral çok küçüktür. Genel durum bundan bir parça daha karışık olabilir, ama bu ruh içinde bir tek frekansın o kadar çok ölçüsü Fourier dönüşümü ve bir fonksiyon f(t) içinde mevcuttur.
-
3 hertz'te salınım gösteren anaç fonksiyon.
-
3 hertz'te Fourier dönüşümü için integrand'ın gerçek ve sanal kısımları
-
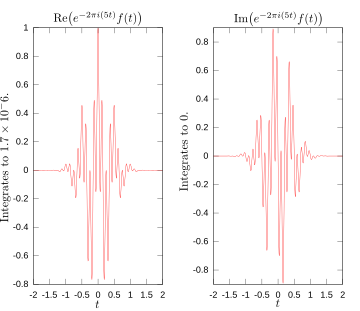
5 hertz'te Fourier dönüşümü için gerçek ve sanal kısımlar
-
3 ve 5 hertz etiketleri ile Fourier dönüşümü.
Temel özellikler
[değiştir | kaynağı değiştir]Fourier dönüşümünün temel özellikleri aşağıdadır: Pinsky 2002.
- Doğrusallık
- Herhangi karmaşık sayılar a ve b için, eğer , ise
- Öteleme
- Herhangi gerçek sayı x0 için, eğer ise
- Modülasyon
- Herhangi gerçek sayı ξ0 için eğer ise
- Ölçekleme
- bir sıfır-dışı gerçek sayılar a için, eğer h(x) = f(ax), ise Durum a = −1 zaman-ters özellik için yer alır, bu durum: eğer h(x) = f(−x), ise
- Eğer then
- Özel olarak, eğer f gerçek ve tek gerçeklik durumu var ise , şöyle ki, bir Hermisyen fonksiyondur.
- Ve eğer f saf sanal, ise
- İntegrasyon
- Yerine koyma tanımı içinde, elde edilen
İşte böyle, başlangıç noktası içinde Fourier dönüşümünün evrimi () tüm domenin üzerinde tüm f in integralinin eşitidir.
Önemli Fourier dönüşümlerinin tabloları
[değiştir | kaynağı değiştir]Aşağıdaki tablolar, bir kapalı bir şekilde Fourier dönüşümleri kaydedebilir.f(x), g(x) ve h(x) fonksiyonlar için burada ile Fourier dönüşümü, sırasıyla ve ile ifade edilir. Sadece en yaygın üç kural dahildir. Bu, bu giriş 105 Fourier Fourier dönüşümü ile ve ters olarak düşünülebilir bir fonksiyonun ve orijinal fonksiyonunun dönüşümü arasında bir ilişki veren fark için yararlı olabilir.
Fonksiyonel ilişkiler
[değiştir | kaynağı değiştir]Bu tabloda Fourier dönüşümleri bulunabilir Erdélyi 1954 veya Kammler 2000, appendix.
| Fonksiyon | Fourier dönüşümü birim, sıradan frekans |
Fourier dönüşümü birim, açısal frekans |
Fourier dönüşümü birim-olmayan, açısal frekans |
Açıklamalar | |
|---|---|---|---|---|---|
|
|
|
|
Tanım | ||
| 101 | Doğrusallık | ||||
| 102 | Zaman domeni içinde kayma | ||||
| 103 | Frekans domeni içinde kayma, 102'nin çifti | ||||
| 104 | zaman domeninde ölçekleme. Eğer is büyük, ise 0 çevresinde yoğunlaşmıştır ve yayılır ve düzleşir. | ||||
| 105 | ikilik.Burada Fourier dönüşümü sütunu olarak aynı yöntem kullanılarak hesaplanması gerekmektedir.
ve veya veya 'ın "yapay" değişkenleri değiştirme sonuçları. | ||||
| 106 | |||||
| 107 | Bu 106'nın çiftidir | ||||
| 108 | gösterimi ve 'in evrişimidir- bu kural evrişim teoremidir | ||||
| 109 | Bu 108'in çiftidir | ||||
| 110 | için saf gerçek | Hermisyen simetridir. karmaşık eşleniklerine ayrılır. | |||
| 111 | için bir saf gerçek çift fonksiyon | , ve saf gerçek çift fonksiyondur. | |||
| 112 | için bir saf gerçek tek fonksiyon | , ve saf sanal tek fonksiyonlar. | |||
| 113 | Karmaşık eşlenik, 110'un genellemesi | ||||
Kare-integrallenebilir fonksiyonlar
[değiştir | kaynağı değiştir]bu tablo içinde Fourier dönüşümleri Campbell & Foster 1948 içinde bulunabilir, Erdélyi 1954 veya Kammler 2000 in eki.
| Fonksiyon | Fourier dönüşümü birim, sıradan frekans |
Fourier dönüşümü birim, açısal frekans |
Fourier dönüşümü birim-olmayan, açısal frekans |
Açıklamalar | |
|---|---|---|---|---|---|
|
|
|
|
|||
| 201 | dörtgen uyarı ve normalleştirilmiş sinc fonksiyon, burada sinc(x) = sin(πx)/(πx) olarak tanımlanır | ||||
| 202 | kural 201'in çifti dörtgen fonksiyon bir ideal alçak-geçiren filtredir ve sinc fonksiyon gibi bir filtrenin nedensel-olmayan uyarı yanıtıdır.sinc fonksiyon burada sinc(x) = sin(πx)/(πx) olarak tanımlanır | ||||
| 203 | tri(x) fonksiyon üçgen fonksiyondur | ||||
| 204 | kural 203'ün ikilisi. | ||||
| 205 | u(x) fonksiyonu Heaviside birim basamak fonksiyon ve a>0. | ||||
| 206 | Bu üniter Fourier dönüşümleri için, Gauss fonksiyonu exp(−αx2), kendi Fourier αnın bazı seçimleri için dönüşüm olduğunu gösterir. Bu İntegrallenebilir olması için biz Re(α)>0 olmalıdır. | ||||
| 207 | a>0 için. Bu, bir bozunmuş üstel fonksiyonun Fourier dönüşümü bir Lorentzyen fonksiyondur. | ||||
| 208 | Hiperbolik sekant Fourier dönüşümünün kendisidir | ||||
| 209 |
|
|
|
Hermit polinomudur. Eğer a = 1 ise Gauss-Hermit fonksiyonları Fourier dönüşüm işlemcisinin özfonksiyonudur.Bir türev için, bakınız Hermit polinomu. Formül n = 0 için 206'ya indirgenir. |
Dağılımlar
[değiştir | kaynağı değiştir]Fourier dönüşümleri bu tablo (Erdélyi 1954) içinde bulunabilir veya Kammler 2000 in eki.
| Fonksiyon | Fourier dönüşümü birim, sıradan frekans |
Fourier dönüşümü birim, açısal frekans |
Fourier dönüşümü birim-olmayan, açısal frekans |
Açıklamalar | |
|---|---|---|---|---|---|
|
|
|
|
|||
| 301 | δ(ξ) dağılımı Dirac delta fonksiyonu'nu ifade eder. | ||||
| 302 | 301'in kural ikizi. | ||||
| 303 | Bunu 103 ve 301'den izleyin | ||||
| 304 | 101 ve 303 kuralından aşağıda Euler formülü kullanılıyor:
| ||||
| 305 | 101 ve 303 kuralından aşağıda kullanılıyor | ||||
| 306 | |||||
| 307 | |||||
| 308 | Burada, n bir doğal sayılar sicimi Dirac delta fonksiyonunun türevinin n-inci dağılımıdır. Bu kural 107 ve 301 kuralından izlenir.Bu 101 ile kombine ediliyor,tüm polinomlar dönüştürülbilir. | ||||
| 309 | Burada sgn(ξ) işaret fonksiyonudur. Unutmadan 1/x bir dağılım değildir.Bu fonksiyonların üyelerini test ediyor ise Cauchy temel değeri kullanmak için gereklidir.Bu kural Hilbert dönüşümüçalışmalarında kullanılıyor | ||||
| 310 |
|
1/xn homojen dağılım ve dağılımsal türev ile tanımlanır | |||
| 311 | Bu formül 0 > α > −1 için değerlidir.α > 0 için başlangıçtan ortaya çıkan bazı tekil terimler bu 318 türevi ile bulunabilir. Eğer Re α > −1,ise bir yerel integrallenebilir fonksiyondur ve gibi bir katkılı dağılım.Fonksiyon katkılı dağılımın uzayına sağ yarı düzlemden bir holomorfik fonksiyondur. Bu bir katkılı dağılıma bir benzersiz meromorfik uzantı kabul ediliyor, ayrıca için α ≠ −2, −4, ... ile ifade edilir (bakınız homojen dağılım.) | ||||
| 312 | 309 kuralının ikizidir. Ve yine Cauchy temel değeri olarak düşünüldüğünde gerekli olan Fourier dönüşümüdür,. | ||||
| 313 | u(x) fonksiyonu Heaviside birim basamak fonksiyonudur; 101, 301 ve 312 kurallarından bunu izleyin . | ||||
| 314 | Bu fonksiyon Dirac comb fonksiyonu olanarak bilinir. Bu,dağılımlar ile birlikte olarak aslında 302 ve 102 den elde edilebilir sonuçtur | ||||
| 315 | J0(x) fonksiyonu sıfırıncı dereceden birinci türün Bessel fonksiyonudur | ||||
| 316 | Bu 315'in genellemesidir.Fonksiyon Jn(x) n-inci dereceden Besselbirinci türün Bessel fonksiyonudur.Fonksiyon Tn(x) birinci türün Chebyshev polinomudur | ||||
| 317 | Euler–Mascheroni sabitidir. | ||||
| 318 | Bu formül 1 > α > 0 için değerdir. Yüksek üsteller için türev formülüne kullanılan diferansiyasyondur.u Heaviside fonksiyonudur. |
İki-boyutlu fonksiyonlar
[değiştir | kaynağı değiştir]| Fonksiyon | Fourier dönüşümü birim, sıradan frekans |
Fourier dönüşümü birim, açısal frekans |
Fourier dönüşümü birim-olmayan, açısal frekans | |
|---|---|---|---|---|
| 400 |
|
|
| |
| 401 | ||||
| 402 |
- Açıklamalar
400 için: Değişkenler ξx, ξy, ωx, ωy, νx ve νy gerçek sayılardır. Integraller tüm düzlem üzerinde alınır.
401 için: Her iki fonksiyon birim hacmine sahip olmayabilen Gauss vardır.
402 için: Fonksiyon circ(r)=1 0≤r≤1 ile tanımlanır ve 0 diğerleridir. Bu Airy dağılımıdır ve J1 bağıntısı kullanılır (ilk tür'ün derece 1 Bessel fonksiyonu). Stein & Weiss 1971, Thm. IV.3.3
Genel n-boyutlu fonksiyonlar için formüller
[değiştir | kaynağı değiştir]| Fonksiyon | Fourier dönüşümü birim, sıradan frekans |
Fourier dönüşümü birim, açısal frekans |
Fourier dönüşümü birim olmayan,açısal frekans | |
|---|---|---|---|---|
| 500 |
|
|
| |
| 501 | ||||
| 502 | ||||
| 503 | ||||
| 504 |
- Açıklamalar
501 için: Fonksiyon χ[0, 1] aralığının gösterge işlevi [0, 1]. Fonksiyonu Γ(x) gama fonksiyonudur. Jn/2 + δ fonksiyonu için n/2 + δ ile, birinci tür bir Bessel işlevidir.n = 2 alınması ve δ = 0 402 üretir. Stein & Weiss 1971, Thm. 4.15
502 için: Riesz potansiyeline bakınız. Formül Analitik devamlılığı ile tüm α ≠ −n, −n − 1, … için tutar, ama sonra fonksiyonu ve onun Fourier dönüşümlerinin uygun düzenlilestirmeye katkılı dağılımları olarak anlaşılması gerekir - formül aynı zamanda tüm α ≠-n,-n için de geçerlidir. Homojen dağılıma bakın.
503 için: Bu, 0 ortalama ile 1 normalize bir çok değişkenli normal dağılım için formül Bold değişkenler vektörler ve matrislerdir. Anılan sayfa ifadenin ardından, and
504 için: Burada .BakınızStein & Weiss 1971, s. 6
Ayrıca bakınız
[değiştir | kaynağı değiştir]- Matematiksel fonksiyonların listesi
- Ayrık Fourier dönüşümü
- Fourier serisi
- Fraksiyonel fourier dönüşümü
- Dolaylı Fourier dönüşümü
- NGC 4622,NGC 4622 Fourier dönüşümü özellikle görüntü m = 2.
- Z-dönüşümü
Kaynakça
[değiştir | kaynağı değiştir]- ^ İngilizce Vikipedi'den çevrilmiştir. 18 Aralık 2023.
- Boashash, B., (Ed.) (2003), Time-Frequency Signal Analysis and Processing: A Comprehensive Reference, Oxford: Elsevier Science, ISBN 0-08-044335-4
- Bochner S., Chandrasekharan K. (1949), Fourier Transforms, Princeton University Press
- Bracewell, R. N. (2000), The Fourier Transform and Its Applications (3. bas.), Boston: McGraw-Hill, ISBN 0-07-116043-4.
- Campbell, George; Foster, Ronald (1948), Fourier Integrals for Practical Applications, New York: D. Van Nostrand Company, Inc..
- Condon, E. U. (1937), "Immersion of the Fourier transform in a continuous group of functional transformations", Proc. Nat. Acad. Sci. USA, cilt 23, ss. 158-164.
- Duoandikoetxea, Javier (2001), Fourier Analysis, American Mathematical Society, ISBN 0-8218-2172-5.
- Dym, H; McKean, H (1985), Fourier Series and Integrals, Academic Press, ISBN 978-0-12-226451-1.
- Erdélyi, Arthur, (Ed.) (1954), Tables of Integral Transforms, 1, New Your: McGraw-Hill
- Fourier, J. B. Joseph (1822), Théorie Analytique de la Chaleur, Paris: Chez Firmin Didot, père et fils, 28 Mart 2014 tarihinde kaynağından arşivlendi, erişim tarihi: 17 Haziran 2014
- Fourier, J. B. Joseph; Freeman, Alexander, translator (1878), The Analytical Theory of Heat, The University Press, 28 Mart 2014 tarihinde kaynağından arşivlendi, erişim tarihi: 17 Haziran 2014
- Grafakos, Loukas (2004), Classical and Modern Fourier Analysis, Prentice-Hall, ISBN 0-13-035399-X.
- Grafakos, Loukas; Teschl, Gerald (2013), "On Fourier transforms of radial functions and distributions", J. Fourier Anal. Appl., cilt 19, ss. 167-179, doi:10.1007/s00041-012-9242-5.
- Hewitt, Edwin; Ross, Kenneth A. (1970), Abstract harmonic analysis. Vol. II: Structure and analysis for compact groups. Analysis on locally compact Abelian groups, Die Grundlehren der mathematischen Wissenschaften, Band 152, Berlin, New York: Springer-Verlag, MR 0262773.
- Hörmander, L. (1976), Linear Partial Differential Operators, Volume 1, Springer-Verlag, ISBN 978-3-540-00662-6.
- James, J.F. (2011), A Student's Guide to Fourier Transforms (3. bas.), New York: Cambridge University Press, ISBN 978-0-521-17683-5.
- Kaiser, Gerald (1994), A Friendly Guide to Wavelets, Birkhäuser, ISBN 0-8176-3711-7, 28 Mart 2014 tarihinde kaynağından arşivlendi, erişim tarihi: 17 Haziran 2014
- Kammler, David (2000), A First Course in Fourier Analysis, Prentice Hall, ISBN 0-13-578782-3
- Katznelson, Yitzhak (1976), An introduction to Harmonic Analysis, Dover, ISBN 0-486-63331-4
- Knapp, Anthony W. (2001), Representation Theory of Semisimple Groups: An Overview Based on Examples, Princeton University Press, ISBN 978-0-691-09089-4
- Pinsky, Mark (2002), Introduction to Fourier Analysis and Wavelets, Brooks/Cole, ISBN 0-534-37660-6, 28 Mart 2014 tarihinde kaynağından arşivlendi, erişim tarihi: 17 Haziran 2014
- Polyanin, A. D.; Manzhirov, A. V. (1998), Handbook of Integral Equations, Boca Raton: CRC Press, ISBN 0-8493-2876-4.
- Rudin, Walter (1987), Real and Complex Analysis (Third bas.), Singapore: McGraw Hill, ISBN 0-07-100276-6.
- Rahman, Matiur (2011), Applications of Fourier Transforms to Generalized Functions, WIT Press, ISBN 1845645642, 28 Mart 2014 tarihinde kaynağından arşivlendi, erişim tarihi: 17 Haziran 2014.
- Stein, Elias; Shakarchi, Rami (2003), Fourier Analysis: An introduction, Princeton University Press, ISBN 0-691-11384-X, 28 Mart 2014 tarihinde kaynağından arşivlendi, erişim tarihi: 17 Haziran 2014.
- Stein, Elias; Weiss, Guido (1971), Introduction to Fourier Analysis on Euclidean Spaces, Princeton, N.J.: Princeton University Press, ISBN 978-0-691-08078-9, 28 Mart 2014 tarihinde kaynağından arşivlendi, erişim tarihi: 17 Haziran 2014.
- Taneja, HC (2008), "Chapter 18: Fourier integrals and Fourier transforms", Advanced Engineering Mathematics:, Volume 2, New Delhi, India: I. K. International Pvt Ltd, ISBN 8189866567, 28 Mart 2014 tarihinde kaynağından arşivlendi, erişim tarihi: 17 Haziran 2014.
- Titchmarsh, E (1948), Introduction to the theory of Fourier integrals (2. bas.), Oxford University: Clarendon Press (1986 tarihinde yayınlandı), ISBN 978-0-8284-0324-5.
- Wilson, R. G. (1995), Fourier Series and Optical Transform Techniques in Contemporary Optics, New York: Wiley, ISBN 0-471-30357-7.
- Yosida, K. (1968), Functional Analysis, Springer-Verlag, ISBN 3-540-58654-7.













































































































































































































































![{\displaystyle \displaystyle \chi _{[0,1]}(|\mathbf {x} |)(1-|\mathbf {x} |^{2})^{\delta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82cc3ddf9072ee7e78288074568e7005d5bb7f91)














