Laplace denklemi
Matematikte Laplace denklemi, özellikleri ilk defa Pierre-Simon Laplace tarafından çalışılmış bir kısmi diferansiyel denklemdir. Laplace denkleminin çözümleri, elektromanyetizma, astronomi ve akışkanlar dinamiği gibi birçok bilim alanında önemlidir çünkü çözümler bilhassa elektrik ve yerçekim potansiyeli ile akışkan potansiyelinin davranışını açıklar. Laplace denkleminin çözümlerinin genel teorisi aynı zamanda potansiyel teorisi olarak da bilinmektedir.
Tanım[değiştir | kaynağı değiştir]
Üç boyutta, problem x, y ve z gibi üç gerçel değişkene sahip ve iki kere türevlenebilir. Laplace denkleminin çözümlerine aynı zamanda harmonik fonksiyonlar da denmektedir. Laplace ve Poisson denklemleri eliptik kısmi diferansiyel denklemlerin en basit örnekleridir. Kısmi diferansiyel operatörü olan ve herhangi bir boyutta tanımlanabilen 'ye veya 'ya Laplasyen işlemcisi veya kısaca Laplasyen denmektedir.
veya
Bu sıklıkla
olarak yazılır veya,daha genel kavramlar içinde özel olarak,
burada ∆ = ∇2 Laplace operatörü veya "Laplasyen"dir
burada ∇ • diverjans işlemcidir ("div" ile sembolize edilir) bu skalerler için vektörler gönderme ve ∇ gradyan işlemcidir ("grad" ile ifade edilir) bu vektörler için skaler göndermedir. (bu nedenle, Laplasyen Δf ≝ div grad f, bir skaler büyüklük için skaler f fonksiyonu göndermedir ; özellikle bu bir skaler için (fonksiyon) f'in vektör grad (kısmi türevler) göndermesidir.)
Eğer sağ-el taraf verilen özel bir fonksiyon ise, h(x, y, z), yani, Eğer böyle bir denklem
ise "Poisson denklemi" denir.
Laplace denklemi ayrıca Helmholtz denkleminin özel bir durumudur.
Not:Delta sembolü, Δ, ayrıca "bir değişiklik içinde" bazı çokluklar gösterim için yaygın olarak kullanılıyor,yani ∆Q ≝ Q + δ veya ∆Q ≝ Q + εQ bazı çok küçük skalerler δ veya ε için. Laplasyen temsil kullanımı bu kullanım ile karıştırılmamalıdır. Laplace ve Poisson denklemleri eliptik kısmi diferansiyel denklemlerin en basit örnekleridir. Kısmi diferansiyel operatörü olan ve herhangi bir boyutta tanımlanabilen 'ye veya 'ya Laplace operatörü veya kısaca Laplasyen denmektedir.
Sınır koşulları[değiştir | kaynağı değiştir]
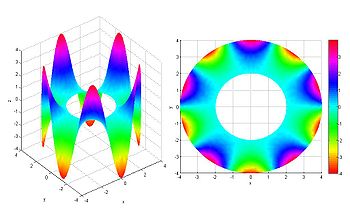
Laplace denklemi için Dirichlet problemi bir D bölgesi üzerinde tanımlı ve verilmiş başka bir fonksiyona D 'nin sınırı üzerinde eşit olan bir fonksiyonu bulmaktan ibarettir. Laplace operatörü ısı denkleminde yer aldığı için, problemin bir diğer yorumu da şöyledir: Bölgenin sınırındaki sıcaklık sabit tutulur ve bölgenin iç tarafındaki sıcaklık artık değişmeyecek şekilde beklenilir. İç bölgedeki sıcaklık dağılımı artık ilişkin Dirichlet probleminin çözümü tarafından verilecektir.
Laplace denklemi için Neumann sınır koşulları D'nin sınırında fonsiyonunu belirtmez ancak bu fonksiyonun normal türevini belirtir. Fiziksel olarak bu durum, yalnız 'nin sınırında etkisi bilinen bir vektör alanı için olan bir potansiyelin inşasına (oluşturulmasına) denk gelmektedir.
Laplace denkleminin çözümlerine harmonik fonksiyonlar denilmektedir ve bu fonksiyonların hepsi denklemin sağlandığı bölge içinde analitiktir. Eğer iki fonksiyon Laplace denkleminin (veya herhangi doğrusal homojen diferansiyel denklemin) çözümüyse, toplamları (veya herhangi doğrusal kombinasyonları) da ayrıca bir çözümdür. Süperpozisyon ilkesi de denilen bu özellik özellikle karmaşık problemlerin basit çözümlerin toplanılması yoluyla yapılan çözümlerinde çok yararlıdır.
İki boyutta Laplace denklemi[değiştir | kaynağı değiştir]
İki değişkenli Laplace denklemi
formuna sahiptir.
Analitik fonksiyonlar[değiştir | kaynağı değiştir]
Karmaşık analitik bir fonksiyonun gerçel ve sanal kısmının her ikisi de Laplace denklemini sağlar. Eğer z=x+iy ise ve
ise, o zaman f(z) 'nin analitik olması için gerekli koşul aşağıdaki Cauchy-Riemann denklemlerinin sağlanmasıdır:
Takip eden ifade ise
olacaktır. Bu yüzden u Laplace denklemini sağlar. Benzer bir hesaplama yine v 'nin de Laplace denklemini sağladığını gösterir.
Aksine diğer taraftan bir harmonik fonksiyon verilirse, bu fonksiyon analitik bir fonksiyonunun gerçel kısmı olur (en azından yerel olarak). Eğer
olarak alınırsa ve
şartı konulursa, o zaman Cauchy-Riemann denklemleri sağlanacaktır.
Bu ilişki ψ'yi belirlemese de artışlarını belirler:
φ için Laplace denklemi ψ'nin integrallenebilme koşulunun sağlandığını gösterir:
ve bu yüzden ψ bir çizgi integrali yoluyla tanımlanabilir. İntegrallenebilme koşulu ve Stoke teoremi iki noktayı birleştiren çizgi integralinin değerinin takip edilen yoldan bağımsız olduğunu gösterir. Laplace denkleminin sonucunda çıkan çözüm çiftine eşlenik harmonik fonksiyonlar adı verilir. Bu inşa sadece yerel olarak veya takip edilen yolun bir tekilliği çevrelememesi koşuluyla geçerlidir. Örneğin, r ve θ kutupsal koordinatlar olursa ve
ise, o zaman karşılık gelen analitik fonksiyon
fonksiyonudur. Bununla birlikte, θ açısı orijini çevrelemeyen bir bölge içinde tek (bir) değerlidir.
Laplace denklemi ve analitik fonksiyonlar arasındaki yakın ilişki Laplace denkleminin çözümünün her mertebeden türevi olduğunu gösterir ve bu çözüm en azından bir tekilliği çevrelemeyen bir çember içinde kuvvet serilerine genişletilebilir. Bu durum, daha az düzenliliğe sahip ısı denklemi çözümleriyle tezat bir haldedir.
Kuvvet serileri ve Fourier serileri arasında sıkı bir ilişki vardır. Bir f fonksiyonu R yarıçaplı bir çember içinde kuvvet serisine genişletilirse, bu gerçel ve sanal kısımları
şeklinde olan uygun katsayıların olduğu
ifadesi anlamına gelir. Bu yüzden,
olur ki bu da f 'nin Fourier seridir.
Akışkan akımı[değiştir | kaynağı değiştir]
u ve v nicelikleri durağan sıkıştırılamaz, dönmez bir akımın iki boyutta yatay ve dikey bileşenleri olsun. Akımın sıkıştırılamaz olmasının koşulu,
olmasıdır ve akımın dönmez olmasının şartı da
olmasıdır. Bir ψ fonksiyonunun diferansiyeli
olarak tanımlanırsa, o zaman sıkıştırılamama şartı bu diferansiyel için integrallenebilme koşulu olur: Sonuçtaki fonksiyona akış fonksiyonu adı verilir çünkü bu fonksiyon akım çizgileri boyunca sabittir. ψ'nin birinci türevi
ile verilir ve sıkıştırılamama şartı ψ 'nin Laplace denklemini sağladığını gösterir. ψ 'ye eşlenik olan harmonik φ fonksiyonuna hız potansiyeli denilir. Cauchy-Riemann denklemleri
ifadesini verir.
Bu yüzden her analitik fonksiyon düzlemde durağan sıkıştırılamaz, dönmez bir akışkan akıma karşılık gelir. Gerçel kısım hız potansiyeli olurken sanal kısım akış fonksiyonu olur.
Elektrostatik[değiştir | kaynağı değiştir]
Maxwell denklemleri'ne göre, iki uzay boyutunda yer alan ve zamandan bağımsız olan bir elektrik alanı (u,v),
ifadesini ve ρ'nun yük yoğunluğu olduğu
ifadesini sağlar.
Birinci Maxwell denklemi
diferansiyeli için integrallenebilme koşuludur. Böylece elektrik potansiyeli olan φ
ifadesini sağlayacak şekilde inşa edilebilir.
İkinci Maxwell denklemi o zaman Poisson denklemi olarak ifade edilen
denklemini verir.
İki boyutta kullanılana benzer olarak, Laplace denklemi elektrostatik ve akışkan akımının üç boyutlu problemlerinde de kullanılabilir.
Üç boyutta Laplace denklemi[değiştir | kaynağı değiştir]
Temel çözüm[değiştir | kaynağı değiştir]
Laplace denkleminin temel çözümü, Dirac delta fonksiyonu 'nın noktasında toplanmış bir birim kaynağı gösterdiği
denklemini sağlar. Hiçbir fonksiyon bu özelliğe sahip değildir ancak yine de bu, integralleri uzay üzerinde birlik olan ve desteği (fonksiyonun sıfır olmadığı bölge) bir noktaya küçülen bir fonksiyonlar limiti olarak düşünülebilir. Temel çözümün tanımı bu yüzden, u 'nun Laplasyeninin kaynak noktasını çevreleyen herhangi bir hacim üzerinde integrali alındığında, o zaman
olduğunu gösterir.
Laplace denklemi koordinatların rotasyonuyla değişmez kalır ve bu yüzden bir temel çözümün, sadece (kaynak noktasından uzaklığı gösteren) r 'ye bağımlı olan çözümler arasından elde edilebileceği beklenir. Hacim kaynak noktası etrafında a yarıçaplı bir top olarak düşünülürse, o zaman Gauss diverjans teoremi
ifadesini verir. O zaman takip eden ifade ise, kaynak noktası etrafında r yarıçaplı bir küre üzerindeki
ifadesidir ve bu yüzden
olur. Benzer bir hesap ise iki boyutta
olduğunu gösterir.
Green fonksiyonu[değiştir | kaynağı değiştir]
Bir Green fonksiyonu da bir V hacminin S sınırındaki uygun şartı sağlayan temel bir çözümdür. Örneğin, ,
ifadelerini sağlayabilir.
Eğer u, V üzerinde Poisson denkleminin herhangi bir çözümüyse
olur ve u, S üzerinde g sınır değerlerini alır. O zaman aşağıdaki eşitlikleri veren (diverjans teoreminin bir sonucu olan) Green özdeşliğine başvurulabilir:
un ve Gn gösterimleri S üzerindeki normal türevleri ifade etmektedir. u ve G 'nin sağladığı şartlar bağlamında, bu sonuç
haline gelir.
Bu yüzden, Green fonksiyonu f ve g 'nin noktalarındaki etkisini açıklar. a yarıçaplı kürenin içi düşünüldüğünde ise, Green fonksiyonu yansıtma yoluyla elde edilebilir (Sommerfeld, 1949): Kürenin merkezinden ρ kadar uzaklıkta olan P kaynak noktası,
uzaklıkta bulunan bir N noktasına yarıçapsal doğru boyunca yansıtılır.
Unutulmaması gereken nokta P küre içindeyse, N 'nin küre dışında olması gerektiğidir. O zaman Green fonksiyonu R 'nin P kaynak noktasına uzaklığı ve T 'nin yansıtılmış N noktasına olan uzaklığı gösterdiği
ifadesi tarafından verilir. Green fonksiyonu için olan bu ifadenin bir sonucu ise Poisson integral formülüdür. ρ, θ ve φ, P kaynak noktası için küresel koordinatlar olsun. Burada θ dikey eksenle olan açıyı göstermektedir. (Amerikan matematik gösterimine uymaz ancak standard Avrupa ve fiziksel uygulamalarına uyum gösteren bir gösterimdir) O zaman, küre içindeki Laplace denkleminin çözümü
olarak alınırsa
tarafından verilir.
Bu formülün basit bir sonucu ise şudur: u harmonikse, o zaman u 'nun kürenin merkezindeki değerleri, u 'nun küre üzerindeki değerlerinin ortalama değerleridir. Bu ortalama değer özelliği ise ivedilikle sabit olmayan bir fonksiyonun maksimum değerini kürenin içinde alamayacağı sonucunu verir.
Ayrıca bakınız[değiştir | kaynağı değiştir]
- 6-küre koordinatlar, bir koordinat sistemi altında bu Laplace's denklemi becomes R-ayrılabilir
- Helmholtz denklemi,Laplace's denkleminin genel bir durumu.
- Bateman dönüşümü
- Earnshaw's teoremi stabil statik ferromanyetik süspansiyonun imkânsız olduğunu göstermek için Laplace denklemi kullanır
- Vektör Laplasyen
- Küresel harmonikler
- Dörtlük bölgeler
- Potansiyel teorisi
- Potansiyel akımı
Kaynakça[değiştir | kaynağı değiştir]
- L.C. Evans, Partial Differential Equations, American Mathematical Society, Providence, 1998. ISBN 0-8218-0772-2 -- Kısmi Diferansiyel Denklemler.
- I. G. Petrovsky, Partial Differential Equations, W. B. Saunders Co., Philadelphia, 1967 -- Kısmi Diferansiyel Denklemler.
- A. D. Polyanin, Handbook of Linear Partial Differential Equations for Engineers and Scientists, Chapman & Hall/CRC Press, Boca Raton, 2002. ISBN 1-58488-299-9 -- Mühendisler ve Biliminsanları için Doğrusal Kısmi Diferansiyel Denklemler El Kitabı.
- A. Sommerfeld, Partial Differential Equations in Physics, Academic Press, New York, 1949 -- Fizikte Kısmi Diferansiyel Denklemler.
Dış bağlantılar[değiştir | kaynağı değiştir]
- "Laplace Denklemi (özel çözümler ve sınır değer problemleri)" (PDF). EqWorld: The World of Mathematical Equations. 25 Ağustos 2005 tarihinde kaynağından (PDF) arşivlendi..
- "Laplace Diferansiyel Denklemi". PlanetMath. 24 Haziran 2008 tarihinde kaynağından arşivlendi..
- "Başlangıç Değer Problemleri Örnekleri". exampleproblems.com. 3 Temmuz 2017 tarihinde kaynağından arşivlendi..
- "MathWorld'teki Laplace Denklemi bilgisi". MathWorld. 3 Ağustos 2008 tarihinde kaynağından arşivlendi.
- John H. Mathews. "Laplace Denklemi Modülü". 7 Nisan 2013 tarihinde kaynağından arşivlendi..
- Whye-Teong Ang. "A Beginner's Course in Boundary Element Methods". 7 Şubat 2012 tarihinde kaynağından arşivlendi.
Laplace denklemi tarafından hükmedilen sınır değer problemlerinin sınır öğesi metoduyla nasıl nümerik olarak nasıl çözülebileceğinin araştırılabileceği bir site



























![{\displaystyle f(z)=\sum _{n=0}^{\infty }\left[a_{n}r^{n}\cos n\theta -b_{n}r^{n}\sin n\theta \right]+i\sum _{n=1}^{\infty }\left[a_{n}r^{n}\sin n\theta +b_{n}r^{n}\cos n\theta \right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/988aaaa979f84297a0203a14fb424ba381f4fc23)





















![{\displaystyle \iiint _{V}\left[G\,\nabla \cdot \nabla u-u\,\nabla \cdot \nabla G\right]\,dV=\iiint _{V}\nabla \cdot \left[G\nabla u-u\nabla G\right]\,dV=\iint _{S}\left[Gu_{n}-uG_{n}\right]\,dS.\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b42331f8ae6edb5abb438f575369019cba8f4d3)





