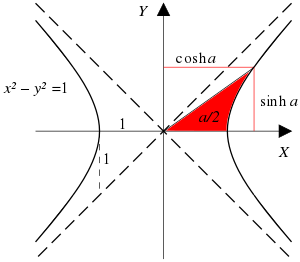
Orijinden geçen bir ışın
x
2
−
y
2
=
1
{\displaystyle \scriptstyle x^{2}\ -\ y^{2}\ =\ 1}
(
cosh
a
,
sinh
a
)
{\displaystyle \scriptstyle (\cosh \,a,\,\sinh \,a)}
a
{\displaystyle \scriptstyle a}
x
{\displaystyle \scriptstyle x}
x
{\displaystyle \scriptstyle x}
bakınız . Matematikte , hiperbolik fonksiyonlar sıradan trigonometrik fonksiyonların analogudur. Temel hiperbolik fonksiyonlar hiperbolik sinüs "sinh", hiperbolik kosinüs "cosh", bunlardan türetilen hiperbolik tanjant "tanh"[1] Ters hiperbolik fonksiyonlar alan hiperbolik sinüsü "arsinh" ("asinh" ya da "arcsinh" olarak da gösterilir)[2]
(cos t , sin t ) noktalarının birim yarıçaplı bir çember oluşturması gibi, (cosh t , sinh t ) noktaları da eşkenar hiperbolün sağ yarısını oluşturur. Hiperbolik fonksiyonlar, zincir eğrisini tanımlayan denklem ile elekromanyetik teori , ısı transferi , akışkanlar dinamiği ve özel görelilik gibi fiziğin çeşitli alanlarında önemli bir denklem olan Kartezyen koordinat sisteminde Laplace denklemi gibi lineer diferansiyel denklemlerin çözümlerinde görülür.
Hiperbolik açı adı verilen gerçek bağımsız değişkenler için hiperbolik fonksiyonların değeri de gerçektir. Karmaşık analizde ise basitçe üstel fonksiyonların rasyonel fonksiyonlarıdır , dolayısıyla meromorf fonksiyonlardır .
Hiperbolik fonksiyonlar, 1760'larda birbirlerinden bağımsız olarak Vincenzo Riccati ve Johann Heinrich Lambert tarafından tanımlanmıştır.[3] Sc. ve Cc. ([co]sinus circulare ) hiperbolik fonksiyonlar için ise Sh. ve Ch. ([co]sinus hyperbolico ) kısaltmalarını kullanmıştır. Lambert aynı isimleri kullanmış ancak kısaltma olarak günümüzde kullanılan kısaltmaları kullanmıştır.[4] sh ve ch kısaltmaları Fransızca ve Rusça gibi bazı dillerde günümüzde de kullanılmaktadır.
sinh , cosh ve tanh csch , sech ve coth (b) sinh(
x )
ex ile
e−x fonksiyonlarının
farkının yarısıdır
(a) cosh ve (b) sinh hiperbolik fonksiyonları
e
x
{\displaystyle e^{x}}
ve
e
−
x
{\displaystyle e^{-x}}
üstel fonksiyonları kullanılarak elde edilmiştir
Hiperbolik fonksiyonlar şunlardır:
sinh
x
=
e
x
−
e
−
x
2
=
e
2
x
−
1
2
e
x
{\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}={\frac {e^{2x}-1}{2e^{x}}}}
cosh
x
=
e
x
+
e
−
x
2
=
e
2
x
+
1
2
e
x
{\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}={\frac {e^{2x}+1}{2e^{x}}}}
tanh
x
=
sinh
x
cosh
x
=
e
x
−
e
−
x
e
x
+
e
−
x
=
e
2
x
−
1
e
2
x
+
1
{\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{2x}-1}{e^{2x}+1}}}
coth
x
=
cosh
x
sinh
x
=
e
x
+
e
−
x
e
x
−
e
−
x
=
e
2
x
+
1
e
2
x
−
1
{\displaystyle \coth x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}={\frac {e^{2x}+1}{e^{2x}-1}}}
sech
x
=
(
cosh
x
)
−
1
=
2
e
x
+
e
−
x
=
2
e
x
e
2
x
+
1
{\displaystyle \operatorname {sech} \,x=\left(\cosh x\right)^{-1}={\frac {2}{e^{x}+e^{-x}}}={\frac {2e^{x}}{e^{2x}+1}}}
csch
x
=
(
sinh
x
)
−
1
=
2
e
x
−
e
−
x
=
2
e
x
e
2
x
−
1
{\displaystyle \operatorname {csch} \,x=\left(\sinh x\right)^{-1}={\frac {2}{e^{x}-e^{-x}}}={\frac {2e^{x}}{e^{2x}-1}}}
Hiperbolik fonksiyonlar karmaşık düzlemde dairesel açılarla da ifade edilebilir:
sinh
x
=
−
i
sin
i
x
{\displaystyle \sinh x=-{\rm {i}}\sin {\rm {i}}x\!}
cosh
x
=
cos
i
x
{\displaystyle \cosh x=\cos {\rm {i}}x\!}
tanh
x
=
−
i
tan
i
x
{\displaystyle \tanh x=-{\rm {i}}\tan {\rm {i}}x\!}
coth
x
=
i
cot
i
x
{\displaystyle \coth x={\rm {i}}\cot {\rm {i}}x\!}
sech
x
=
sec
i
x
{\displaystyle \operatorname {sech} \,x=\sec {{\rm {i}}x}\!}
csch
x
=
i
csc
i
x
{\displaystyle \operatorname {csch} \,x={\rm {i}}\,\csc \,{\rm {i}}x\!}
i , i 2 = −1 olarak tanımlanan sanal birimdir .
Yukarıdaki denkliklerin karmaşık sayı biçimleri Euler denkleminden gelir.
Kabul edilen konvansiyon gereği, sinh2 x , (sinh x )2 anlamına gelir ve sinh(sinh x ) demek değildir. Bu kabul pozitif üstler ile diğer hiperbolik fonksiyonlar için de geçerlidir. Hiperbolik kotanjant fonksiyonu ctnh x olarak da yazılır ama coth x gösterimi daha yaygındır.
sinh
(
−
x
)
=
−
sinh
x
{\displaystyle \sinh(-x)=-\sinh x\,\!}
cosh
(
−
x
)
=
cosh
x
{\displaystyle \cosh(-x)=\cosh x\,\!}
Dolayısıyla:
tanh
(
−
x
)
=
−
tanh
x
{\displaystyle \tanh(-x)=-\tanh x\,\!}
coth
(
−
x
)
=
−
coth
x
{\displaystyle \coth(-x)=-\coth x\,\!}
sech
(
−
x
)
=
sech
x
{\displaystyle \operatorname {sech} (-x)=\operatorname {sech} \,x\,\!}
csch
(
−
x
)
=
−
csch
x
{\displaystyle \operatorname {csch} (-x)=-\operatorname {csch} \,x\,\!}
cosh x ve sech x çift fonksiyon , diğerleri tek fonksiyondur .
arsech
x
=
arcosh
1
x
{\displaystyle \operatorname {arsech} \,x=\operatorname {arcosh} {\frac {1}{x}}}
arcsch
x
=
arsinh
1
x
{\displaystyle \operatorname {arcsch} \,x=\operatorname {arsinh} {\frac {1}{x}}}
arcoth
x
=
artanh
1
x
{\displaystyle \operatorname {arcoth} \,x=\operatorname {artanh} {\frac {1}{x}}}
Hiperbolik sinüs ve kosinüs, Pisagor trigonometrik özdeşliği 'ne benzeyen aşağıdaki özdeşliği sağlar
cosh
2
x
−
sinh
2
x
=
1
{\displaystyle \cosh ^{2}x-\sinh ^{2}x=1\,}
Diğer fonksiyonlar için de şu özdeşlikler sağlanır
tanh
2
x
=
1
−
sech
2
x
{\displaystyle \tanh ^{2}x=1-\operatorname {sech} ^{2}x}
coth
2
x
=
1
+
csch
2
x
{\displaystyle \coth ^{2}x=1+\operatorname {csch} ^{2}x}
Hiperbolik tanjant nonlineer sınır değeri probleminin çözümüdür:[5]
1
2
f
″
=
f
3
−
f
;
f
(
0
)
=
f
′
(
∞
)
=
0
{\displaystyle {\frac {1}{2}}f''=f^{3}-f\qquad ;\qquad f(0)=f'(\infty )=0}
cosh x eğrisinin altındaki alanın her zaman yay uzunluğuna eşit olduğu gösterilebilir:[6]
alan
=
∫
a
b
cosh
x
d
x
=
∫
a
b
1
+
(
d
d
x
cosh
x
)
2
d
x
=
yay uzunluğu
.
{\displaystyle {\text{alan}}=\int _{a}^{b}{\cosh {x}}\ dx=\int _{a}^{b}{\sqrt {1+\left({\frac {d}{dx}}\cosh {x}\right)^{2}}}\ dx={\text{yay uzunluğu}}.}
arsinh
x
=
ln
(
x
+
x
2
+
1
)
{\displaystyle \operatorname {arsinh} \,x=\ln \left(x+{\sqrt {x^{2}+1}}\right)}
arcosh
x
=
ln
(
x
+
x
2
−
1
)
;
x
≥
1
{\displaystyle \operatorname {arcosh} \,x=\ln \left(x+{\sqrt {x^{2}-1}}\right);x\geq 1}
artanh
x
=
1
2
ln
1
+
x
1
−
x
;
|
x
|
<
1
{\displaystyle \operatorname {artanh} \,x={\tfrac {1}{2}}\ln {\frac {1+x}{1-x}};\left|x\right|<1}
arcoth
x
=
1
2
ln
x
+
1
x
−
1
;
|
x
|
>
1
{\displaystyle \operatorname {arcoth} \,x={\tfrac {1}{2}}\ln {\frac {x+1}{x-1}};\left|x\right|>1}
arsech
x
=
ln
1
+
1
−
x
2
x
;
0
<
x
≤
1
{\displaystyle \operatorname {arsech} \,x=\ln {\frac {1+{\sqrt {1-x^{2}}}}{x}};0<x\leq 1}
arcsch
x
=
ln
(
1
x
+
1
+
x
2
|
x
|
)
{\displaystyle \operatorname {arcsch} \,x=\ln \left({\frac {1}{x}}+{\frac {\sqrt {1+x^{2}}}{\left|x\right|}}\right)}
d
d
x
sinh
x
=
cosh
x
{\displaystyle {\frac {d}{dx}}\sinh x=\cosh x\,}
d
d
x
cosh
x
=
sinh
x
{\displaystyle {\frac {d}{dx}}\cosh x=\sinh x\,}
d
d
x
tanh
x
=
1
−
tanh
2
x
=
sech
2
x
=
1
/
cosh
2
x
{\displaystyle {\frac {d}{dx}}\tanh x=1-\tanh ^{2}x={\hbox{sech}}^{2}x=1/\cosh ^{2}x\,}
d
d
x
coth
x
=
1
−
coth
2
x
=
−
csch
2
x
=
−
1
/
sinh
2
x
{\displaystyle {\frac {d}{dx}}\coth x=1-\coth ^{2}x=-{\hbox{csch}}^{2}x=-1/\sinh ^{2}x\,}
d
d
x
csch
x
=
−
coth
x
csch
x
{\displaystyle {\frac {d}{dx}}\ {\hbox{csch}}\,x=-\coth x\ {\hbox{csch}}\,x\,}
d
d
x
sech
x
=
−
tanh
x
sech
x
{\displaystyle {\frac {d}{dx}}\ {\hbox{sech}}\,x=-\tanh x\ {\hbox{sech}}\,x\,}
d
d
x
arsinh
x
=
1
x
2
+
1
{\displaystyle {\frac {d}{dx}}\,\operatorname {arsinh} \,x={\frac {1}{\sqrt {x^{2}+1}}}}
d
d
x
arcosh
x
=
1
x
2
−
1
{\displaystyle {\frac {d}{dx}}\,\operatorname {arcosh} \,x={\frac {1}{\sqrt {x^{2}-1}}}}
d
d
x
artanh
x
=
1
1
−
x
2
{\displaystyle {\frac {d}{dx}}\,\operatorname {artanh} \,x={\frac {1}{1-x^{2}}}}
d
d
x
arcsch
x
=
−
1
|
x
|
1
+
x
2
{\displaystyle {\frac {d}{dx}}\,\operatorname {arcsch} \,x=-{\frac {1}{\left|x\right|{\sqrt {1+x^{2}}}}}}
d
d
x
arsech
x
=
−
1
x
1
−
x
2
{\displaystyle {\frac {d}{dx}}\,\operatorname {arsech} \,x=-{\frac {1}{x{\sqrt {1-x^{2}}}}}}
d
d
x
arcoth
x
=
1
1
−
x
2
{\displaystyle {\frac {d}{dx}}\,\operatorname {arcoth} \,x={\frac {1}{1-x^{2}}}}
∫
sinh
a
x
d
x
=
a
−
1
cosh
a
x
+
C
{\displaystyle \int \sinh ax\,dx=a^{-1}\cosh ax+C}
∫
cosh
a
x
d
x
=
a
−
1
sinh
a
x
+
C
{\displaystyle \int \cosh ax\,dx=a^{-1}\sinh ax+C}
∫
tanh
a
x
d
x
=
a
−
1
ln
(
cosh
a
x
)
+
C
{\displaystyle \int \tanh ax\,dx=a^{-1}\ln(\cosh ax)+C}
∫
coth
a
x
d
x
=
a
−
1
ln
(
sinh
a
x
)
+
C
{\displaystyle \int \coth ax\,dx=a^{-1}\ln(\sinh ax)+C}
∫
d
u
a
2
+
u
2
=
sinh
−
1
(
u
a
)
+
C
{\displaystyle \int {\frac {du}{\sqrt {a^{2}+u^{2}}}}=\sinh ^{-1}\left({\frac {u}{a}}\right)+C}
∫
d
u
u
2
−
a
2
=
cosh
−
1
(
u
a
)
+
C
{\displaystyle \int {\frac {du}{\sqrt {u^{2}-a^{2}}}}=\cosh ^{-1}\left({\frac {u}{a}}\right)+C}
∫
d
u
a
2
−
u
2
=
a
−
1
tanh
−
1
(
u
a
)
+
C
;
u
2
<
a
2
{\displaystyle \int {\frac {du}{a^{2}-u^{2}}}=a^{-1}\tanh ^{-1}\left({\frac {u}{a}}\right)+C;u^{2}<a^{2}}
∫
d
u
a
2
−
u
2
=
a
−
1
coth
−
1
(
u
a
)
+
C
;
u
2
>
a
2
{\displaystyle \int {\frac {du}{a^{2}-u^{2}}}=a^{-1}\coth ^{-1}\left({\frac {u}{a}}\right)+C;u^{2}>a^{2}}
∫
d
u
u
a
2
−
u
2
=
−
a
−
1
sech
−
1
(
u
a
)
+
C
{\displaystyle \int {\frac {du}{u{\sqrt {a^{2}-u^{2}}}}}=-a^{-1}\operatorname {sech} ^{-1}\left({\frac {u}{a}}\right)+C}
∫
d
u
u
a
2
+
u
2
=
−
a
−
1
csch
−
1
|
u
a
|
+
C
{\displaystyle \int {\frac {du}{u{\sqrt {a^{2}+u^{2}}}}}=-a^{-1}\operatorname {csch} ^{-1}\left|{\frac {u}{a}}\right|+C}
C sabit sayıdır.
Yukarıdaki fonksiyonları Taylor dizisi olarak da göstermek mümkündür:
sinh
x
=
x
+
x
3
3
!
+
x
5
5
!
+
x
7
7
!
+
⋯
=
∑
n
=
0
∞
x
2
n
+
1
(
2
n
+
1
)
!
{\displaystyle \sinh x=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}}
sinh x fonksiyonunun Taylor dizisi gösteriminde x için yalnızca tek üstel bileşenler bulunur. Tek fonksiyon olduğundan ötürü −sinh x = sinh(−x ) ve sinh 0 = 0 doğrudur.
cosh
x
=
1
+
x
2
2
!
+
x
4
4
!
+
x
6
6
!
+
⋯
=
∑
n
=
0
∞
x
2
n
(
2
n
)
!
{\displaystyle \cosh x=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}}
cosh x fonksiyonunun Taylor dizisi gösteriminde x için yalnızca çift üstel bileşenler bulunur. Dolayısıyla çift fonksiyondur yani y -eksenine göre simetriktir. sinh ve cosh dizilerinin toplamı üstel fonksiyonun sonsuz dizi gösterimidir.
tanh
x
=
x
−
x
3
3
+
2
x
5
15
−
17
x
7
315
+
⋯
=
∑
n
=
1
∞
2
2
n
(
2
2
n
−
1
)
B
2
n
x
2
n
−
1
(
2
n
)
!
,
|
x
|
<
π
2
{\displaystyle \tanh x=x-{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\cdots =\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}},\left|x\right|<{\frac {\pi }{2}}}
coth
x
=
x
−
1
+
x
3
−
x
3
45
+
2
x
5
945
+
⋯
=
x
−
1
+
∑
n
=
1
∞
2
2
n
B
2
n
x
2
n
−
1
(
2
n
)
!
,
0
<
|
x
|
<
π
{\displaystyle \coth x=x^{-1}+{\frac {x}{3}}-{\frac {x^{3}}{45}}+{\frac {2x^{5}}{945}}+\cdots =x^{-1}+\sum _{n=1}^{\infty }{\frac {2^{2n}B_{2n}x^{2n-1}}{(2n)!}},0<\left|x\right|<\pi }
Laurent dizisi )
sech
x
=
1
−
x
2
2
+
5
x
4
24
−
61
x
6
720
+
⋯
=
∑
n
=
0
∞
E
2
n
x
2
n
(
2
n
)
!
,
|
x
|
<
π
2
{\displaystyle \operatorname {sech} \,x=1-{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}-{\frac {61x^{6}}{720}}+\cdots =\sum _{n=0}^{\infty }{\frac {E_{2n}x^{2n}}{(2n)!}},\left|x\right|<{\frac {\pi }{2}}}
csch
x
=
x
−
1
−
x
6
+
7
x
3
360
−
31
x
5
15120
+
⋯
=
x
−
1
+
∑
n
=
1
∞
2
(
1
−
2
2
n
−
1
)
B
2
n
x
2
n
−
1
(
2
n
)
!
,
0
<
|
x
|
<
π
{\displaystyle \operatorname {csch} \,x=x^{-1}-{\frac {x}{6}}+{\frac {7x^{3}}{360}}-{\frac {31x^{5}}{15120}}+\cdots =x^{-1}+\sum _{n=1}^{\infty }{\frac {2(1-2^{2n-1})B_{2n}x^{2n-1}}{(2n)!}},0<\left|x\right|<\pi }
Laurent dizisi )
B
n
{\displaystyle B_{n}\,}
n inci Bernoulli sayısıdır
E
n
{\displaystyle E_{n}\,}
n inci Euler sayısıdır Dairesel trigonometrik fonksiyonlarla karşılaştırma [ değiştir | kaynağı değiştir ] Kartezyen düzlemin aşağıdaki iki altkümesi ele alındığında
A
=
{
(
cosh
t
,
sinh
t
)
:
t
∈
R
}
ve
B
=
{
(
cos
t
,
sin
t
)
:
t
∈
R
}
.
{\displaystyle A=\lbrace (\cosh t,\sinh t):t\in R\rbrace \quad {\text{ve}}\quad B=\lbrace (\cos t,\sin t):t\in R\rbrace .}
A birim hiperbolün sağ dalını oluşturur iken
{(x,y ): x 2 − y 2 = 1},
B birim çemberi oluşturur. Doğal olarak
A
∩
B
{\displaystyle A\cap B}
t → B periyodik fonksiyon iken t → A değildir.
Hiperbolik fonksiyonlar trigonometrik özdeşliklere biçimsel olarak benzeyen birçok özdeşliği sağlar. Aslında, Osborn kuralı [7]
sinh
(
x
+
y
)
=
sinh
x
cosh
y
+
cosh
x
sinh
y
{\displaystyle \sinh(x+y)=\sinh x\cosh y+\cosh x\sinh y\,}
cosh
(
x
+
y
)
=
cosh
x
cosh
y
+
sinh
x
sinh
y
{\displaystyle \cosh(x+y)=\cosh x\cosh y+\sinh x\sinh y\,}
tanh
(
x
+
y
)
=
tanh
x
+
tanh
y
1
+
tanh
x
tanh
y
{\displaystyle \tanh(x+y)={\frac {\tanh x+\tanh y}{1+\tanh x\tanh y}}\,}
"çift değişken formülleri"
sinh
2
x
=
2
sinh
x
cosh
x
{\displaystyle \sinh 2x\ =2\sinh x\cosh x\,}
cosh
2
x
=
cosh
2
x
+
sinh
2
x
=
2
cosh
2
x
−
1
=
2
sinh
2
x
+
1
{\displaystyle \cosh 2x\ =\cosh ^{2}x+\sinh ^{2}x=2\cosh ^{2}x-1=2\sinh ^{2}x+1\,}
tanh
2
x
=
2
tanh
x
1
+
tanh
2
x
{\displaystyle \tanh 2x\ ={\frac {2\tanh x}{1+\tanh ^{2}x}}\,}
ve "yarım değişken formülleri":[8]
sinh
x
2
=
1
2
(
cosh
x
−
1
)
{\displaystyle \sinh {\tfrac {x}{2}}={\sqrt {{\tfrac {1}{2}}(\cosh x-1)}}\,}
cosh
x
2
=
1
2
(
cosh
x
+
1
)
{\displaystyle \cosh {\tfrac {x}{2}}={\sqrt {{\tfrac {1}{2}}(\cosh x+1)}}\,}
sinh x 'in türevi cosh x ve cosh x 'in türevi sinh x 'tır. Bu dairesel fonksiyonlara benzer ancak işareti farklıdır (örneğin, cos x 'in türevi −sin x 'tir).
Gudermannian fonksiyonu karmaşık sayıları içermeyen hiperbolik fonksiyonlar ile dairesel fonksiyonlar arasında doğrudan bağıntıları verir.
a cosh(x /a ) fonksiyonunun grafiği zincir eğrisi , yani uniform esnek bir zincirin iki sabit noktadan asıldığında uniform yerçekimi kuvveti etkisiyle oluşturduğu eğridir.
Hiperbolik sinüs ve kosinüs tanımlarından aşağıdaki özdeşlikleri çekebiliriz:
e
x
=
cosh
x
+
sinh
x
{\displaystyle e^{x}=\cosh x+\sinh x\!}
ve
e
−
x
=
cosh
x
−
sinh
x
.
{\displaystyle e^{-x}=\cosh x-\sinh x.\!}
Bu gösterimler, karmaşık üstel fonksiyonların toplamı olarak, Euler denklemine göre sinüs ve kosinüs gösterimlerine benzerdir.
Karmaşık sayılar için hiperbolik fonksiyonlar [ değiştir | kaynağı değiştir ] Herhangi bir karmaşık değişken için üstel fonksiyon tanımlanabildiği için hiperbolik fonksiyonların tanımları karmaşık değişkenlere de uygulanabilir. Dolayısıyla sinh z ve cosh z fonksiyonları holomorf fonksiyondur .
Karmaşık sayılar için trigonometrik fonksiyonlar Euler denklemi ile verilir:
e
i
x
=
cos
x
+
i
sin
x
{\displaystyle e^{ix}=\cos x+i\;\sin x}
e
−
i
x
=
cos
x
−
i
sin
x
{\displaystyle e^{-ix}=\cos x-i\;\sin x}
dolayısıyla:
cosh
i
x
=
1
2
(
e
i
x
+
e
−
i
x
)
=
cos
x
{\displaystyle \cosh ix={\tfrac {1}{2}}(e^{ix}+e^{-ix})=\cos x}
sinh
i
x
=
1
2
(
e
i
x
−
e
−
i
x
)
=
i
sin
x
{\displaystyle \sinh ix={\tfrac {1}{2}}(e^{ix}-e^{-ix})=i\sin x}
cosh
(
x
+
i
y
)
=
cosh
(
x
)
cos
(
y
)
+
i
sinh
(
x
)
sin
(
y
)
{\displaystyle \cosh(x+iy)=\cosh(x)\cos(y)+i\sinh(x)\sin(y)\,}
sinh
(
x
+
i
y
)
=
sinh
(
x
)
cos
(
y
)
+
i
cosh
(
x
)
sin
(
y
)
{\displaystyle \sinh(x+iy)=\sinh(x)\cos(y)+i\cosh(x)\sin(y)\,}
tanh
i
x
=
i
tan
x
{\displaystyle \tanh ix=i\tan x\,}
cosh
x
=
cos
i
x
{\displaystyle \cosh x=\cos ix\,}
sinh
x
=
−
i
sin
i
x
{\displaystyle \sinh x=-i\sin ix\,}
tanh
x
=
−
i
tan
i
x
{\displaystyle \tanh x=-i\tan ix\,}
Dolayısıyla hiperbolik fonksiyonlar
2
π
i
{\displaystyle 2\pi i}
π
i
{\displaystyle \pi i}
Karmaşık düzlemde hiperbolik fonksiyonlar
sinh
(
z
)
{\displaystyle \operatorname {sinh} (z)}
cosh
(
z
)
{\displaystyle \operatorname {cosh} (z)}
tanh
(
z
)
{\displaystyle \operatorname {tanh} (z)}
coth
(
z
)
{\displaystyle \operatorname {coth} (z)}
sech
(
z
)
{\displaystyle \operatorname {sech} (z)}
csch
(
z
)
{\displaystyle \operatorname {csch} (z)}
^ "tanh" (PDF) . 31 Ekim 2017 tarihinde kaynağından arşivlendi (PDF) . Erişim tarihi: 19 Aralık 2011 . ^ Some examples of using arcsinh . Google Books 'ta bulunan örnekler.^ Robert E. Bradley, Lawrence A. D'Antonio, Charles Edward Sandifer. Euler at 300: an appreciation. Mathematical Association of America, 2007. Page 100.
^ Georg F. Becker. Hyperbolic functions. Read Books, 1931. Page xlviii.
^ Eric W. Weisstein . "Hyperbolic Tangent" . MathWorld . 11 Eylül 2015 tarihinde kaynağından arşivlendi . Erişim tarihi: 20 Ekim 2008 . ^ N.P., Bali (2005). Golden Intergral Calculus ISBN 8-170-08169-6 . 22 Haziran 2013 tarihinde kaynağından arşivlendi . Erişim tarihi: 19 Aralık 2011 . Extract of page 472 22 Haziran 2013 tarihinde Wayback Machine sitesinde arşivlendi .^ G. Osborn, Mnemonic for hyperbolic formulae [ölü/kırık bağlantı
^ Peterson (2003). Technical mathematics with calculus ISBN 0-766-86189-9 . 22 Haziran 2013 tarihinde kaynağından arşivlendi . Erişim tarihi: 19 Aralık 2011 . Chapter 26, page 1155 22 Haziran 2013 tarihinde Wayback Machine sitesinde arşivlendi .