Güven aralığı
Bu madde, Vikipedi biçem el kitabına uygun değildir. (Eylül 2018) |
Güven aralığı, istatistik biliminde bir anakütle parametresi için bir çeşit aralık kestirimi olup bir çıkarımsal istatistik çözüm aracıdır. Bir anakütle parametre değerinin tek bir sayı ile kestirimi yapılacağına, bu parametre değerini kapsayabilecek iki (alt ve üst sınır) sayıdan oluşan bir aralık bulunur. Böylece güven aralıkları bir kestirimin ne kadar güvenilir olduğunu gösterir.
Bulunan aralığın anakütle parametresini içine alıp kapsamasının ne kadar olasılığı bulduğu güven düzeyi veya güven katsayısı ile belirlenir. Bir güven aralığı her zaman, bir yüksek yüzde orantı olarak ifade edilen, bir güven düzeyi ile birlikte verilir; örneğin geleneksel olarak istatistikçiler %99 güven aralığı veya %95 güven aralığı veya %90 güven aralığı şeklinde ifadeler kullanırlar. Bir güven aralığının iki uç (alt ve üst) noktası güven sınırları olarak anılır. Arzu edilen güven düzeyini yükseltmek, güven aralığının genişlemesine yol açar. Herhangi verilmiş bir durumda kullanılan kestirim yöntemi için, güven düzeyi gittikçe büyültülürse, çıkartılan güven aralığı da gittikçe genişleyecektir.
Bir güven aralığının hesaplanması, genel olarak kestirim yönteminin özellikleri hakkında gayet belirli varsayımların yapılmasını gerektirir. Bundan açıktır ki güven aralığı hesaplaması bir parametik çıkarımsal analiz aracıdır. Örneğin bir anakütle ortalaması hakkında çıkarım yapmak için örneklem verileri kullanılarak hazırlanan bir anakütle ortalaması güven aralığı kurmak için, örneklemin rastgele olduğunu ve bu rastgele örneklem verilerinin de normal dağılım gösteren bir anakütleden geldiği varsayımı yapılır. Bu nedenle burada incelen güven aralıklarının güçlü istatistik konumunda olmaları gerekmez; ama herhangi bir güven aralığında belirli bazı değişiklikler yapılarak - yani güçlü güven aralığı şekline sokularak - güven aralığına güçlü istatistik karakteri de kazandırılabilir.
Genel olarak güven aralıkları Neyman–Pearson tipi "çokluluk (frequentist) olasılık" temel teorisine dayanmaktadır. Bayes tipi istatistik temel teorisi kullanılırsa, benzer bir parametrik çıkarımsal analiz aracı, bir inanılır aralık, ortaya çıkartılır. Ancak güven aralığı ve inanılır aralık değişik teorik ve felsefi temellere dayanan kavramlardır ve genellikle aynı verilerden değişik güven ve inanılır aralıkları ortaya çıkartılır. Çoklulukçu objektif ve Bayes tipi subjektif olasılık temel felsefeleri hakkında temelden bir uyuşmazlık olduğu gibi, istatistikçiler arasında güven aralığı veya inanılır aralık kullanılması gereği ve yararlığı hakkında büyük uyuşmazlık bulunmaktadır.
Kavramsal temel[değiştir | kaynağı değiştir]

Aralık kestirimleri ile nokta kestirimlerini karşılaştırmakta fayda bulunmaktadır. Bir nokta kestirim ilgi duyulan anakütle parametrenin tahmin değeri olarak verilmiş tek bir sayı değeridir. Buna karşıt olarak, aralık kestiriminde anakütle parametresinin içinde bulunduğu, alt ve üst sınırı sayı değerleri olan bir aralık yayılımı verilir. Kestirimlerin güvenilirliğini daha iyice belirtmek için istatistik çalışmalarda tablolar ve grafiklerde tek bir nokta kestirim değeri yanında bir kestirim aralığı (alt ve üst sınır) değerleri de verilir.
Bir örneğin için bir seçimden önce yapılan bir seçim sondaj sonuçlarının ne kadar güvenilir olduğunu belirlemek istenebilir. Uygun bir seçmen örnekleminde bulunan seçmenlere sorulan bir sorudan bu örnekleme dahil olanların %40'ının belirli bir partiye oy verme kararı olduğu öğrendiği kabul edilsin. Bu örneklem oranı olan %40, anakütle oranı olarak kullanılınca, bu bir nokta kestirim olur ve tüm seçmenlerin %40'ının belirli partiye oy verecekleri kestirimi yapılabilir. Aynı örneklem verileri kullanılarak anakütle belirli partiye oy verenle oranı için "%90 güven aralığı" kurulabilir ve bu aralığın %36 ile %44 arasında olduğu bulunabilir ve "%95 güven aralığı" ise %36 ile %44 olarak elde edilir. Herhangi belirtilmiş bir güven düzeyi için (diğer her şey değişmeden aynı kalırsa) daha az yaygın bir güven aralığı daha çok yaygın bir güven aralığından daha fazla inanılır sonuç verir. Bir güven aralığının yaygınlığına etki eden büyük bir faktör kestirim hesaplanması için kullanılan örneklem büyüklüğüdür; yani örneklemle elde edilen gerçek veri değerlerin kaç tane olduğudur.
Güven bölgesi güven aralığı kavramını çoklu değişkenli haller değerlerine genelleştirir. Bu güven bölgeleri sadece kestirim hatalarını olasılık derecelerini vermekle kalmazlar ayrıca bir değişken için kestirim değerinin diğer değişken için kestirim değerinden daha fazla veya daha az güvenilir olup olmadığını da gösterirler. Bakınız güven bandları.
Birçok uygulamalı çalışmalarda %95 güven düzeyi için tek bir güven aralığı göreneksel olarak verilir.[1] Fakat eğer grafikler de verilmekte ise adet olarak birkaç güven düzeyi için (%50, %95, %99) güven aralıkları verilir.
İstatistiksel kuram[değiştir | kaynağı değiştir]
Tanımlama[değiştir | kaynağı değiştir]
Rassal aralıklar olarak güven aralığı[değiştir | kaynağı değiştir]
Güven aralıkları belirli verilmiş veri setine dayanarak hesaplanır. Bir veri seti için tipik gözlemler değerleri x ile ifade edilir ve X aynı anakütleden gözlenmesi mümkün olabilecek sonucu ifade eder. Burada X gerçek sayı değeri x olan bir rassal değişken olur ve X = x ifadesi gözlemlenen bir gerçek sayı değerini ifade eder. Bir güven aralığı bir çift u(.) (alt) ve v(.) (üst) fonksiyonlar ile belirlenir ve belirli bir veri seti için güven aralığı (u(x), v(x)) aralığı ile tanımlanır. Bir güven aralığı tanımını tamamlamak için güven aralığının verdiği aralık kestiriminin konusu olan değer hakkında gayet açık anlayış bulunması gerekmektedir. Bu değerin w olduğu kabul edilsin. u(.) ve v(.) fonksiyonlarını, (u(x), v(x)) aralığını w için en yakın güven aralığı yapabilmek için nitelik, üç-noktalarını rassal değişkenler olarak işlem gören (u(X), v(X)) ile verilen bir seri rassal aralıkların nitelikleriyle ilişkilidir. Bu nitelik wyi de içinde bulunduran rassal aralığın olasılığı c yani
olur ve kapsama olasılığı olarak isimlendirilir.
Burada U = u(X) ve V = v(X) üç noktaları istatistik olurlar yani gerçekte gözlemlenen veri seti değerlerinden ortaya çıkarılmış bir gözlemlenen rassal değişkendirler. Rassal aralık (U, V) olarak ifade edilir.
İstatistiksel çıkarım için güven aralıkları[değiştir | kaynağı değiştir]
Yukarıda verilen bilgilerin istatistiksel çıkarım için uygulanır bir yol olması bir başka etaptan da geçmek gereklidir: kestirimi yapılacak miktar ile X sonucunun olasılık dağılımı. Bu olasılık dağılımı bir gözlemlenemeyecek ama kestiriminin yapılması istenen miktar parametresi (theta θ) ile ve diğer gözlemlenemeyecek ama kestiriminin bilinmesi istenmeyen parametreleri temsil eden (phi φ) ile belirlensin. Kestiriminin bilinmesi istenmeyen diğer parametreler φ istatistikte rahatsız edici parametreler olarak isimlendirilir ama bir kenara atılıp göz yumulamaz miktarlardır ve istatistiksel kuramın bunları ele alıp kurama koymak için bir yol bulması gerekir
φ için 0 ile 1 arasında herhangi bir sayı olan α oranda bir güven aralığı şöyle tanımlanır:
ve burada
ve u(X) ve v(X) gözlemlenebilen rassal değişkenler olurlar. Buna göre gözümleyemeyen θe etki yapan gözlemlenmeyen φ parametrelerin değerlerinin bilinmesi, ü(X) ve v(X) değerlerini bilmek için gerekmemektedir.
Bazen bir yüzde olarak ifade edilen 100%·(1 − α) veya (1 − α) sayısı güven düzeyi veya bazen de güven katsayısı olarak isimlendirilir. Burada Prθ,φ olasılık ifadesi ;(θ, φ) ile belirtilen dağılımı olan X rassal değişkeninin olasılığıdır. Bu belirtilmenin önemli bir açıklaması θ parametresinin gerçek doğru değeri ne olursa olsun, (U, V) rassal aralığının θ'nin bilinmeyen değerini yüksek olasılıkla kapsamaktadır.
Dikkat edilmesi gerek bir başka nokta da, Prθ,φ olasılık terimin modeli gayet ayrınıtıl olarak geliştirilmiş olan olasılık dağılımlarından herhangi birine uyması gerekmemektedir; ama çok kere pratik sorunlarda belirli bir dağılıma uyabilir. Nasıl rassal değişken X, aynı anakütleden ve gerçeğin aynı versiyonundan gelen x için diğer mümkün gerçekleşmeleri temsil ettiğini kabul edersen, benzer açıklamayla (θ, φ) parametreler, X için dağılımların değişik nitelikleri olan değişik gerçek versiyonu ele almamız gerektiğine işaret ettiğini kabul etmek gerekir..
Rassal sonuçlar için güven aralıkları[değiştir | kaynağı değiştir]
Güven aralıkları yukarıda belirtildiği gibi sabit değerler için tanımladığı gibi, rassal miktarlar için de tanımlanabilir. (Örneğin tahmin etme araligi). Bunu yapabilmek için X parametresine istatistiksel bağımsız veya bağımlı olabilen, bir ek tek-değerli bir rassal değişken Y ele almak gerekir. O zaman (u(x), v(x)) aralığını kurmak için kullandığımız kural, eğer
ifadesi gerçek ise, Y parametresinin daha-gözümü-yapılabilecek değeri olan x için bir güven aralığı ortaya çıkarmak mümkündür. Bu şartlı ifadede Prθ,φ (θ, φ) ile belirtilen ve (X, Y) rassal değişkenlerin ortak dağılımını gösterir.
Yaklaşık güven aralıkları[değiştir | kaynağı değiştir]
Bazı standart olmayan uygulamalarda, bir güven aralığı kurabilmek için gerekli olan niteliklere tıpatıp uymayan hallere rastlanma mümkündür. Bu hallerde, kurallara uymakla beraber, pratikte yararlı olabilecek yaklaşık güven aralığı bulunabilir. Bir rassal değişken için kapsama olasılığı c(θ, φ)
ile tanımlanır ve eger kabul edilebilir bir yaklaşım düzeyine ulaştığı bilinip kabul edilirse, bir yaklaşık güven aralığı kurabilmek için kullanılacak kural şöyle verilir.
Güven aralıkları ile Bayes tıpı inanılır aralıkların karşılaştırılması[değiştir | kaynağı değiştir]
Bayes tıpı güven aralık kestimine inanılır aralık ismi verilmektedir. Yukarıda verilenlere uyan bir notasyon kullanırsak, θ parametresini bilinmeyen doğru değeri için bir inanılır aralık tanımlaması şöyledir:[2] Belirli bir α
Burada (küçük theta) Θ bilinmeyen θ parametre değerinin rassal değişken olduğunu vurgulayarak işaret etmek için kullanılmaktadır.
İki değişik tipdeki aralığın tanımlanmalrinin karşılaştırması şöyle yapılabilir:
- Bir güven aralığının tanımlaması verilmiş (θ, φ) için (veya bu değerlere şartlı olarak bağımlı) X için dağılımdan hesaplanmış olasılıkları içerir.
- Bir inanılır aralığın tanımı ise X = x gözümlemmış değerlerinin Φ değerleri üzerinde marjinalize edilmiş (veya ortalaması alınmış) değerlerine şartlı olan Θ parametresinin dağılımından hesaplanmış olasılıkları içerir.
Bu açıklamalarda çok kere rahatsızlık edici parametrelerin ele alınıp incelenmesi bir kenara bırakılmıştır. Ancak bu incelemeler yapılırsa iki değişik aralık şeklinde açıklamaların çok göze çarpar şekilde çok değişik şekilde olacağı bilinmektedir.
Bazı basit standart haller için aynı veriyi kullanarak elde edilen güven aralığı ve inanılır aralık birbiriyle çakışır şekilde birbiriyle aynıdır. Ancak Bayes-tıpı analiz için ya çok ılımlı şekilde veya çok güçlü şekilde önsel enformasyon kullanılmakta ise, bu iki tip aralık, aynı veri ile her zaman çok değişik sonuç çıkartılacaktır.
Burada Θ notasyonu θ nin bilinmeyen değerIenin bir rassal değişken olarak kabul edildiği gereceğini vurgulamak için kullanılmaktadır. İki tip aralık için tanımlamalar şöyle karşılaştırılabilirler:
- Bir "güven aralığı"nin tanımlanması verilmiş (θ, φ)'e göre (veya bu değerlere koşullu olan) X için dağılım ve bu koşulun (θ, φ) ifadesinin tüm değerleri için gerçek olduğu şartını kullanılarak hesaplanmış olan olasılık değerlerini gerektirir.
- Bir "inanılır aralık" tanımlanması için X = x gözümdenmiş değerleri ve bunların Φ değerlerine göre marginilize edilmesi (veya ortalaması alınması) ile elde edilen değerlerden ortaya çıkartılan olasılık değerlerini gerektirir. Bu Φ, değeri φ "sıkıntı veren parametreleri (nuisance parameters)" olan φ değerlerinin belirsizliğini gösteren rassal değişkendir.
Suna dikkati çekilmelidir ki güven aralığı ve inanılır aralıkların karşılaştırılmalarının ele alındığı birçok kaynakta "sıkıntı veren parametreleri (nuisance parameters)" hakkında hiçbir bilgi verilmemektedir; ama bu parametrelerin ele alınması iki yöntemde değişiktir ve değişik yaklaşım gösterilmesini gerektirmektedir
Bazı standart hallerde, "güven aralığı" ve "inanılabilir aralık" yaklaşımları kullanılarak ortaya çıkartılan aralıklar tıpatıp ayni değerlerde olabilirler. Fakat eğer Baye-tipi analiz için kullanılan onsel bilgi cok guclu veya orta güçlü ise bu iki yaklaşıma göre çıkartılan iki aralık değişik değerlerde olacaktır.
Arzu edilir nitelikleri[değiştir | kaynağı değiştir]
Standart istatistiksel yordamlar kullanılmakta iken çok kere güven aralıkları kurmak için özel standart yordamlar kullanılır. Bu yordamlar, eğer yordamın temelinde olan varsayımlara gerçekte de doğru olduğu bilinirse, arzu edilen önceden belirlenmiş bazı nitelikleri karşılamak üzere tasarlanmıştır. Bu arzu edilen nitelikler şunlardır: geçerlilik, optimallik ve değişmezlik. Bunlar arasında en önemlisi geçerlilik olup bunu yakından optimallik takip etmektedir. Değişmezlik genellikle aralığı kurmak için bir kural olmayıp daha çok bir güven aralığını teorik bakımdan ortaya çıkartmak için yöntemin bir niteliğidir. Bu arzu edilen nitelikler standart olmayan güven aralıkları için de aynen geçerlidir.
- Geçerlilik: Bu nitelik güven aralığı için kapsama olasılığının (güven düzeyinin) ya tıpatıp gerçek olması veya iyi bir yaklaşım olarak gerçek olmasıdır.
- Optimallik: Bu nitelik güven aralığının kurulması kurallarının veri setinin kapsadığı enformasyonun mümkün olan en çoğunun kullanılmasıdır. Örneklem veri setinin hemen hemen yarısını bir kenara bırakarak sadece kalan kısmı ile bile bir güven aralığının kurulması mümkün olacağı yukarıdaki açıklamadan bilinmektedir. Optimalilik niteliği hakkında yargıya varmak için bir usul aralığın uzunluğunu yargı kriteri olarak kullanmaktır. Kurulan bir aralık kurulabilen diğer aralıklardan tipik olarak daha dar ise, o aralık diğerlerine nazaran optimallik kriterine daha uygun olduğu kabul edilebilir.
- Değişmezlik: Birçok pratik uygulama için kestirimi yapılacak miktar çok iyice tanımlanmadığı bilinmektedir. Örneğin bir anakütle nüfus için medyan geliri bulmak için bir sondaj örneklem bulunduğu kabul edilsin. Fakat gelirleri açıklamak için kullanılan garfiksel istatistik araçlarında kullanılan ölçek gerçek gelir değil gelirin logarıtmasıdır. Bu nedenle elde edilecek anakütle gelir sonucunun gerçek değil gelirin logarıtması olarak kestirmi yapılması ve güven aralığın tespit edilmesi de uygun bir usul olabilir. Değişmezlik arzu edilen niteliği uygulanırsa hem medyan gelirlerle kurulan bir güven aralığı ve hem de medyan gelirlerin logarıthmaları ile kurulan ve alt ve üst üç aralık noktaları gelir logarıtması olarak ifade edilen güven aralığı kurma sonuçlar için aynı derecede uygundurlar.
Elde edilme yöntemleri[değiştir | kaynağı değiştir]
Standart olmayan uygulamalar için güven aralığı kurmak için bir kural ortaya çıkarmak için çeşitli değişik yollara başvurmak mümkündür. Kabul edilmiş standart yordamları çeşitli değişik yollarla açıklanamak ve kanıtlamak imkânı vardır. Tıpık olarak güven aralığı kurmak için bir kural incelenmekte olan miktar için bir nokta kestirimini bulmak için kullanılan özel üzüle yakından bağlıdır.
- İstatistik: Bu kestirim için kullanılan momentler yöntemine yakından bağlıdır. Basit bir örneğin kestirimi yapılması gereken miktarın anakütle ortalaması olsun; bu halde doğa bir kestirim örneklem ortalaması olur. Yine bir örneklem ortalaması için dağılım varyansının kestirimi için örneklem varyansının uygun olduğu kabul edilmektedir. Doğru anakütle ortalaması için güven aralığı olarak, örneklem ortalamasını merkez alarak aralığın genişliğinin örneklem varyasının kare kökünün bir sabitle çarpımıyla elde edilen çok basit ve naif bir aralık kurabiliriz.
- Olabilirlilik kuramı: Eğer kestirimler maksimum olabilirlik prensibi kullanılarak kurulmuşsa, bu kavramın temelindeki kurama göre kestirmler için güven aralıkları veya güven bölgeleri kurmak için iki değişik yol bulunurur,
- Kestirmci denklemler:Bu halde kestirim yaklaşımı, hem momentler yönteminin genelleştirilmesinden ve hem de maksimum olabilirlik prensibi genelleştirmesinden ortaya çıktığı kabul edilir. Maksimum olabilirlik teorisinin bazı genelleştirilmeleri ile elde edilen sonuçlar kestirimci denklemler kullanılarak ortaya çıkarılan güven aralıklarının bu sonuçlara da uygun olduğu kabul edilmesi neticesi yaratabilir.
- "Anlamlılık sınaması suretiyle": Eğer bir parametrenin genel değerleri için anlamlılık hipotez tezleri kullanmak mümkünse, o zaman güven aralıkları/bölgeleri, doğru değerin sıfır hipotezinde verilen verilen değere eşitliliği (1-p) anlamlılık seviyesinde bir hipotez sınama sonucu olarak retedilmeyen her bir noktayı %100p güven bölgesi içine alarak kurulur.
Örnekler[değiştir | kaynağı değiştir]
Pratik bir örnek[değiştir | kaynağı değiştir]
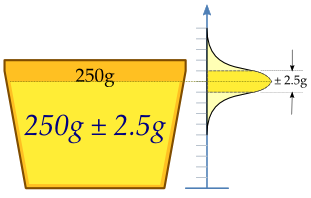
Bir firma ürettiği margarini paketlemek için margarini küçük plastik kaplara dolduran bir makine kullanmaktadır. Bu makine her bir plastik kaba 250g margarin doldurmak üzere ayarlanmıştır. Ancak gerçekte doldurulan her bir kabın muhteviyatı tıpatıp 250g olmayıp bu miktardan ufak farklar göstermektedir. Gerçek muhteviyat bu nedenle rassal değişken X olarak alınabilir. Makinanın ayarının istenilir şekilde olması için muhteviyat rassal değişkeni X, 250g ortalama etrafında ve 2,5g. standart sapma gösteren bir normal dağılıma uyması uygun olduğu kabul edilsin. Bu makinanın ayarının istenilene uygun olup olmadığını belirlemek için gerçekte üretilen dolu plastik kaplardan rastgele bir örneklem alınmıştır ve bunların muhteviyatı ölçülmüştür. Bu rastgele örneklem büyüklüğü n = 25 olsun. Rassal değişken X için bu örneklem değerleri X1, ..., X25 olur.
X için beklenen değer yani normal dağılım parametresi olan anakütle ortalaması μ olsun. Bunun bir uygun kestirimi elde edilen örneklem ortalamasıdır; yani
Bu 25 kaptan oluşan örneklem için gerçek muhteviyat ağırlıkları x1, ..., x25 olarak ifade edilir ve bunların ortalaması (yani örneklem ortalaması) şöyle bulunur:
Bulunan 250,2 örneklem ortalaması anakütle ortalaması μ için bir nokta kestirimi olarak kabul edilebilir. Fakat bilinmektedir ki başka birkaç 25 büyüklükte rastgele örneklem seçilirse örneklem ortalamalar (diyelim) 250,4 veya 251,1 olabilir ama bu örneklem ortalamasının 280 gm olmasının olasılığı çok küçüktür. Gerçekte gözlemlenen kestirim değeri olan 250,2 gm etrafında bir aralık bulunduğu ve eğer gerçek anakütle ortalaması bu aralık içine düşerse, gözlemlenen verinin ender bir şekilde istenilenden değişik olmayacağı kabul edilebilir. Bu türlü aralığa μ parametresi için "güven aralığı" adı verilir. Bu aralığı nasıl hesaplayabiliriz? Aralığın alt ve üst uç noktaları bulmak için elimizde bulunan örneklem verilerini kullanabilir. Böylece aralık uç noktaları bir "istatistik" olurlar; ve X1, ..., X25 örnekleminin fonksiyonu olurlar ve bunlar da rassal değişkenler olurlar.
Elimizdeki problemde anakütle ağırlıkları normal dağılım gösterdiği için örneklem ortalaması da normal dağılım gösterir ve bu örneklem ortalaması normal dağılımı için beklenen değer μ ve standart hatası σ/√n = 0.5 (gram) olur. Böylece örneklem ortalama değerini standardize edebilip z-değerini şöyle bulabiliriz:
Bu ifade içinde kestirimi yapılmak istenen μ parametresine bağlıdır ama bu standart normal dağılım μ parametresine bağımlı değildir. Bu nedenle μ değerinden bağımsız olan ve Z değişkeninin, ne kadar güvenimiz olmasını istediğimizi bildirip ölçen 1 − α, olasılığı ile arasında bulunduğu −z ve z sayılarını bulmak mümkündür. Bu hal için 1 − α = 0.95 olmasını kabul edelim yani
Şu yığmalı dağılım fonksiyonu bulunur
kullanarak z sayısı şöyle bulunur:
Bu sonuç şöyle yorumlanabilir: 0,95 olasılık ile μ parametresinin
ve
stokastık uç noktaları arasında olduğuna dair bir güven aralığı bulunmaktadır.
Bu yorumda şuna dikkati çekmek gerekir: Burada μ parametresinin hesaplanan aralığın içine düşmesinin olasılığı 0,95 olduğu ifade edilmemektedir. Elde edilen güven aralığı şöyle açıklanmaktadır. Her zaman yeni ölçüler alınması tekrarlanınca yeni bir örneklem için ortalama değeri bulunur ve yeni bir güven aralık üç değerleri elde edilebilir. Bu tekrarlama ile elde edilen aralıkların %95ı anakütle μ değerini içinde bulunduracak ve %5 μ değerini ihtiva etmeyecektir.
Buna göre güven aralıkları ortaya çıkartılan -z ve z değerleri formülüne konularak elde edilir. Bundan dolayısı margarın kabı doldurma makinası için anakütle ortalama muhteviyat ağırlığı için %95 güven aralığı şöyle elde edilir:

Parametre μ için istenilen 250gm değeri hesaplanan güven aralığı içinde bulunduğu için, makinenin ayarının bozuk olduğuna inanmaya neden bulunmamaktadır.
Hesaplanan aralık için, μ değeri içinde bulunsa da bulunmasa da, sabit alt ve üst üç değerleri bulunmaktadır. Böylece μnin güven aralığı içinde bulunma olasılığı ya (aralık içinde ise) 1 olur ya da (aralık dışında ise) 0 olur. Bu nedenle güven aralığı kavramı için "parametre μ değerinin güven aralığı içinde bulunma olasılığı (1 − α) olur", şeklinde açıklama yapmak hatalıdır. Yani güven aralığı ve ilişkili güven düzeyi olasılık değerleri değildirler. Güven aralığı tekrar edilen örneklem alınmaları ve her bir örneklem için güven aralıkları hesaplanması halinde bu aralıkların %100(1 − α) oranının parametre μ değerini ihtiva edeceğini bildirmektedir. Bu halde hesaplanan aralıkların %100α oranı parametreyi ihtiva etmeyecektir. Ne yazıktır ki elde edilen örneklemlerin hangisinin güven aralığının parametreyi ihtiva edeceğini bilmemize ve kestirebilmemize imkân yoktur. Bunun için güven aralığı açıklaması "%100(1 − α) güven düzeyi ile μ değeri güven aralığı içinde bulunacaktır" şeklinde yapılmaktadır.
Kenarda verilen gösterim bir simülasyon sonucu vermektedir ve 50 simülasyon gerçekleşmesi için hesaplanıp elde edilen 50 güven aralığının verilen bir düzey doğru olarak verilen μ anakütle ortalama değerini ihtiva edip etmediğini göstermektedir. Eğer rastgele tek bir simülasyon gerçekleşmesi seçersek parametreyi ihtiva edecek bir aralığı seçmemizin olasılığı %95'tir; ancak kader kısmet olarak parametreyi ihtiva etmeyen bir gerçekleşmeyi seçme de mümkündür. Bunun hangisinin gerçeğe çıkacağını bilmemizin imkâni ihtimali yoktur; elimizde bildiğimiz sadece bir güven aralığı vardır!!
Kavramsal örnek[değiştir | kaynağı değiştir]
İstatistiksel anakütle parametreleri ortalaması μ ve varyansi σ2 olan normal dağılımlı bir anakütleden gelen n büyüklüğünde bir rastgele örnekleme seçelim ve her biri diğerinden Bağımsız olan örneklem değerlerinin X1, ..., Xn olarak bulunduğunu kabul edelim.
Bu elde edilen veri değerlerinden "örneklem ortalaması" ve "örneklem varyansı" şöyle bulunur:
O zaman
ifadesi "serbestlik derecesi" n − 1 olan belirli bir Student'in t dağılımı gösterir. Bu ifadede dikkat edilecek nokta T dağılımı ifadesinin gözlemlenemez μ ve σ2; değişkenlerini içinde bulundurmamasıdır.
μ için %90 bir güven aralığı hesaplamak istediğimizi kabul edelim. Bu dağılımın %95 yüzdebirliği c ile ifade edilirse
olur. T nin −c altında bulunması için olasılık %5dir ve +c üstünde olması da %5dır. Böylece T nin −c ve +c sınırları arasına düşme olasılığı %90'dır.
Böylece
olur ve μ için bir teorik (stokastık) %90 güven aralığı elde edilmiş olur.
Örneklemi gözümledikten sonra : için ve S için s değerleri hesaplanabilir. Bunlardan şu güven aralığı hesaplanır:
ve bu sabit üç noktaları olan bir aralıktır. μ bu güven aralığı içindedir veya içinde değildir ve bu aralığın μ parametresini içine alma olasılık değeri hakkında daha başka hiçbir şey söyleme imkânımız bulunmamaktadır.
Ortalama için yaklaşık güven aralığı[değiştir | kaynağı değiştir]
Anakütle için rassal değişken olan sayılar bir normal dağılım göstermiyorlarsa da bir anakütle ortalaması için yaklaşık güven aralığı kurmak merkezsel limit teoremi kullanarak mümkün olabilir. Bu yaklaşık sonuca varmak için kullanılan örneklem büyüklüğü'nün hacminin büyük olması gerekmektedir.[3]
Bu yaklaşık güven aralığı elde etmek için kullanılan formüller gerçekte normal dağılım gösteren anakütleden alınan örneklem verileri için kullanılan formüller ile aynıdır ve çıkartılan yaklaşık güven aralığının yorumlanıp açıklanması aynı şekilde yapılır. Bulunan yaklaşık güven aralığı, eğer anakütle dağılımı hemen hemen normal dağılıma yakın şekilde ise yahut yığmalı dağılım fonksiyonu hiç kesiklikler göstermiyorsa veyahut dağılımın çarpıklıgı pek az ise nispeten küçük sayıda örneklem veri seti elde edilerek uygulanıp kullanılması tavsiye edilmektedir.
Hipotez sınamasına ilişkisi[değiştir | kaynağı değiştir]
Güven aralığı kavramı ve istatistiksel hipotez sınaması kavramının dayandıkları temel varsayımlara ve elde edilen sonuçlara değişiktir. Bu nedenle bu iki çıkartımsal istatistik yöntemlerinin kavramsal olarak ayrı tutulmaları gerekmektedir.
Ancak bu iki değişik yöntem birbirleriyle bazı anlamda bağlantı göstermekte ve bir sınıra kadar birbirini tamamlayıcı görünmektedir. Her türlü güven aralığı böyle kurulmamakla beraber, genellikle bir %100(1−α) güven aralığı için kurma yordamı, θ=θ<şub>0</şub> hipotezinin sınanması sırasında bütün %100α anlamlılık seviyesinde ret edilmeyen θ<şub>0</şub> değerlerinden oluşur. Bu türlü yaklaşım her zaman geçerli olmayabilir; çünkü bu pratikte her zaman uygun bir hipotez sınanmasının elimizde bulunacağını önceden varsaymaktadır. Ama böyle bir hipotez sınanması mevcutsa, bu sınanma için yapılması gereken varsayımların da güven aralığı için de aynen geçerli olması olması gereklidir.
Bir güven aralığının içinde bulunan parametre değerlerinin bir hipotez sınaması ile ret edilmeyen değerlerle genel olarak eşdeğerli olduğunu kabul etmek elverişli bir yaklaşım olabilir; ama bu türlü varsayımı yapmak çok tehlikelidir. Birçok hallerde elde edilen güven aralıkları tam teoriye uyan değerler değil yaklaşık ve ancak genellikle uygun olan değerlerden oluşur ve çok kere "artı veya eksi stardart hatanın bir veya iki misli" şeklinde yaklaşık genellemelerden başka bir şey değildirler; bu genellemelerin güya ilişkili olduğu kabul edilen hipotez sınamalarına nesil bir etki yapacağı ve bu etkinin miktarı ve yönü bilinmemektedir.
Anlamı ve açıklaması[değiştir | kaynağı değiştir]
Olasılığın çokluluk temeline bağlı olduğu teorisini kabul edenler için güven aralığı çeşitli değişik şekillerde yorumlamak mümkündür:
- Güven aralığı örneklemler, daha kesin bir ifade ile (tekrar tekrar arkaarkaya alınan) örneklemler, ile ifade edilebilirler: Cox ve Hinkley "Eğer bu prosedür çoklu sayıda örneklemekle ile çok defa tekrar edilebilseler, (her bir örneklem için değişen) hesaplanmış güven aralığı doğru anakütle parametresini %90 defa kapsayacaktır. ef>Cox, D.R ve Hinkley DV. (1974) Theoretical Statistics, Londra:Chapman and Hall, (İngilizce) say. 49, 209</ref> Kendall ve Stuart bunun aynı anakütleden tekrar tekrar örneklem alma manası olmadığına ve gerekenin sadece teker ve tekrar örneklme alınması gerektiğine işaret etmektedirler.[4]
- Güven aralığı kavramı şöyle açıklanabilir: Cox ve Hinkley'in bir başka yaklaşımı ile "Güven aralığı, bir anakütle parametresinin, %10 anlamlılık derecesinde istatistiksel olarak anlamlı olmayan parametre gerçek değeri ile gözlemlenen kestirim değer farklarının değerlerini temsil eder."
".[5] Bu gerçekten bir güven aralığının kurulmasında kullanılacak özel bir yordamı anlatmaktadır.
- Bir güven aralığına ilişkili olan olasılık bir deneyden-önce görüş açısından ele alınabilir yani üzerinde çalışma yapılan nesnelere tatbik edilen rastgele sağlamalar olarak görülebilir. Bu halde deneyi yapan, önce bir güven aralığı hesaplamayı tasarladığı ve gerçek deneyi yapmaya başlamadan bu aralığın doğru bilinmeyen değeri kapsaması için belirli riskin hesaplanması için kullanılacak bir güven aralığı kurduğu kabul edilmektedir.[6] Bu yukarıda verilen "tekrar edilen örneklemler" yaklaşımına yakındır; ama özellikle gerçekte tekrarlamanın imkânsız olduğu hallerde (örneğin örneklem alıp ölçmenin örneklemi imha etmeyle sonuçlanması) örneklem alma prosedürünün tekrarlamasını teorik varsayımını bir kenara etmektedir.
Yukarıda verilen açıklamalarını bir ortak yanı şudur: Eğer parametrenin doğru değeri hesaplandıktan sonar %90 güven aralığı dışında kalmaktaysa, o zaman şansa dayalı olarak %10 (veya daha az) olasılığı olan bir olay ortaya çıkmıştır.
"Güven" sözcüğünün istatistiksel anlamı[değiştir | kaynağı değiştir]
Alternatifler ve tenkitler[değiştir | kaynağı değiştir]
Güven aralığı aralık kestirimi içinde bir yöntemdir ve "çokluluklu" olasılığı temel alan istatistik pratikte popüler olarak kullanıldığı için en çok kullanılan aralık kestirmi yöntemidir. Bu yöntemin amacı anakütle parametresinin kestirmidir. Çokluluk olasılık temeline bağlı istatistik yöntemlerinde parametre kestirimi yapılacağına gelecekte ortaya çıkabilecek örneklemlerin sonucunun kestirmi de yapılma hedef alınabilir ve o zaman kestirim aralağı kurmak gerekir. Eğer olasılık temelinde Bayes tıpı istatistik olduğu kabul edilirse aralık kestirimi için inanılır aralık kullanılır.
Bu yöntemlerin hangisi kullanılırsa en kullanışlı sonuçların ortay çıkacağı çok tartışmalıdır. Bu üç değişik aralık kestiriminin matematik temelleri üzerinde tartışma bulunmaz ve her ucu de geçerli matematik kullanılarak ortaya çıkartılmıştır ve eğer matematik doğru kullanılmakta ise aynı veri setinden üç değişik matematiksel aralık bulmak mümkündür, Tartışma olasılık kavramının temelinin ne olduğuna dairdir ve daha çok felsefi anlaşmazlıklara dayanır.
Bayes tıpı olasılık temeli felsefesine dayanan istatistikçiler, bir aralık kestirimi ortaya çıkarılınca, bu güven aralığını kestirim aralığı inançlılar gibi "ben bundan sonraki örneklemdem çıkarılam ortalama kestirimim (diyelim) %90 olasılıkla bu aralık içine düşeceğini tahmin ediyorum" demeyip "parametrenin gerçekte bu aralığa düşmesi için benim bilgi "inanç" düzeyim %90'dır" derler.
Güven aralıkları temellerinde olasılıktan çıkartıldığı için normal olasılık yasalarına uymaları gerekir. Eğer birkaç, her biri bağımsızlık varsayıma uyarak hesaplanmış, değişik istatistik ve her birine ait güven aralığı verilirse ya bu bağımsızlık varsayımına uymak gerekir; uyulma kabul edilmezse yapılan hesaplar geçersiz hale gelir. Eğer bir örneklem için birkaç değişik güven aralığı hesaplanmış olup da bunlarda en dar olanını kabul etmek istenirse, bu geçerli bir tutum değildir çünkü bu seçim yapılması halinde yapılan hesaplar geçerli güven aralıkları vermez. Bu seçimi yapmak olasılığı değiştirir ve gerçek aralığı genişletir ve bunun ne kadar olacağını tahmin etmek imkânsızdır.
Bu problem eğer güven aralığı seçmek hipotez sınaması analizi içinde kullanılırsa özellikle önem kazanır. Onun için, bazılarına göre güven aralıklarının hipotez sınaması için kullanılması uygun görülür şeklinde ifadeler bulunmakla beraber, bu açıklama hipotez sınaması için değişik bir yöntem ve değişik bir yorum kullanılması gerektiğine işaret eder.
Oranlar için güven aralıkları ve ilişkili nicelikler[değiştir | kaynağı değiştir]
Ayrıca bakınız[değiştir | kaynağı değiştir]
- p-değeri
- Güven bölgesi
- Hata çubuğu
- Kestirim aralığı
- Tolerans aralığı
- Özyükleme (istatistik)
- Binom oran güven aralığı
- Güçlü güven aralıkları
- Chebyshev eşitsizliği
- Aralık sonlu elemanı
Online hesaplayıcılar[değiştir | kaynağı değiştir]
- TAMU güven aralığı hesaplayıcıları 15 Haziran 2010 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce) (Erişme:24.4.2010)
- GraphPad Çabuk hesaplayıcısı 30 Nisan 2010 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce) (Erişme:24.4.2010)
Dipnotlar[değiştir | kaynağı değiştir]
- ^ Örneğin biyoistatistik çalışmaları için uygulamada. Kaynak: Zar, J.H. (1984) Biostatistical Analysis. Prentice Hall International, New Jersey. pp 43–45
- ^ Bernardo J.E ve Smith, Adrian (2000) Bayesian theory, New York:Wiley ISBN 0-471-49464-X say.259 (İngilizce)
- ^ Bu büyük örneklem büyüklüğü için 20. yüzyılda örneklem veri setinin 30 veya daha büyük sayıda olması yeterli bulunmakta olduğu kabul edilmekteydi. Fakat 2000'li yıllarda bu yaklaşık güven aralığı (ve hipotez sınaması için) 30 sayısının her zaman yeterli olmadığı yapılan kompüter simülasyonu ile gösterilmiştir. Böylece "merkezsel limit teoremi" uygulaması için ekstradan şartlar bulunması gereği ortaya çıkmaktadır.
- ^ Kendall, M.G. ve Stuart, D.G. (1973)The Advanced Theory of Statistics. Vol 2: Inference and Relationship, Londra:Griffin,. Kısım 20.4
- ^ Cox,D.R. ve Hinkley D.V. (1974) Theoretical Statistics, Londra:Chapman ve Hall, say.214, 225, 233
- ^ Neyman, J. (1937) "Outline of a Theory of Statistical Estimation Başed on the Claşsıcal Theory of Probabılıty", Philosophical Transactions of the Royal Society of London A, 236, 333–380.
Kaynakça[değiştir | kaynağı değiştir]
- İngilizce Wikipedia "Confidence intervals" maddesi: [1] 9 Nisan 2010 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce) (Erişme:24.4.2010)
- İngilizce "Usable Statististics" websitesinde kendikendine ogrenme için "Introduction to Confidence intervals" maddesi: [2] 27 Mart 2010 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce) (Erişme:24.4.2010)













![{\displaystyle {\begin{aligned}\Phi (z)&=P(Z\leq z)=1-{\tfrac {\alpha }{2}}=0.975,\\[6pt]z&=\Phi ^{-1}(\Phi (z))=\Phi ^{-1}(0.975)=1.96,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e80e68d525d87d1b722d1150abda18cecb8f684)
![{\displaystyle {\begin{aligned}0.95&=1-\alpha =P(-z\leq Z\leq z)=P\left(-1.96\leq {\frac {{\bar {X}}-\mu }{\sigma /{\sqrt {n}}}}\leq 1.96\right)\\[6pt]&=P\left({\bar {X}}-1.96{\frac {\sigma }{\sqrt {n}}}\leq \mu \leq {\bar {X}}+1.96{\frac {\sigma }{\sqrt {n}}}\right)\\[6pt]&=P\left({\bar {X}}-1.96\times 0.5\leq \mu \leq {\bar {X}}+1.96\times 0.5\right)\\[6pt]&=P\left({\bar {X}}-0.98\leq \mu \leq {\bar {X}}+0.98\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2437ee6c7c0320fa30cec1de64773a6e7cc3a095)










![{\displaystyle \left[{\overline {x}}-{\frac {cs}{\sqrt {n}}},{\overline {x}}+{\frac {cs}{\sqrt {n}}}\right],\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d429a0286ba259bd4a54b3ee7b9572fd3db750ac)