Korelasyon
Korelasyon, olasılık kuramı ve istatistikte iki rassal değişken arasındaki doğrusal ilişkinin yönünü ve gücünü belirtir. Genel istatistiksel kullanımda korelasyon, bağımsızlık durumundan ne kadar uzaklaşıldığını gösterir.
Farklı durumlar için farklı korelasyon katsayıları geliştirilmiştir. Bunlardan en iyi bilineni Pearson çarpım-moment korelasyon katsayısıdır. İki değişkenin kovaryansının, yine bu değişkenlerin standart sapmalarının çarpımına bölünmesiyle elde edilir. Pearson ismiyle bilinmesine rağmen ilk olarak Francis Galton tarafından bulunmuştur.
Pearson çarpım-moment korelasyon katsayısı[değiştir | kaynağı değiştir]
İsimlendirme[değiştir | kaynağı değiştir]
Pearson çarpım-moment korelasyon katsayısı isminde, kovaryans hesaplanırken yapılan işlemin fiziksel moment hesabına benzerliği etkili olmuştur. Çift taraflı bir kaldıraçın iki yük kolundaki ağırlıkların momenti hesaplanırken kullanılan, ağırlık ile ağırlığın destek noktasına olan uzaklığın çarpımı ile her bir değişkenin ortalamaya olan uzaklıklarının bulunması arasındaki benzerlik bu isimlendirmeye neden olmuştur.[1]
Matematiksel özellikleri[değiştir | kaynağı değiştir]
Korelasyon katsayısı, bağımsız değişkenler arasındaki ilişkinin yönü ve büyüklüğünü belirten katsayıdır. Bu katsayı, (-1) ile (+1) arasında bir değer alır. Pozitif değerler direkt yönlü doğrusal ilişkiyi; negatif değerler ise ters yönlü bir doğrusal ilişkiyi belirtir. Korelasyon katsayısı 0 ise söz konusu değişkenler arasında doğrusal bir ilişki yoktur.
Matematik beklenti değerleri μX ve μY, standart sapmaları σX ve σY olan iki bağımsız değişken X ve Y arasındaki Pearson'un çarpım-moment korelasyon katsayısı (ρX, Y), şu şekilde tanımlanır:
E değişkenin matematiksel beklenti değerini, cov ise kovaryansı ifade eder,
μX = E(X) olduğundan, σX2 = E(X2) - E2(X) ve
Y, için de aynısı geçerli olduğundan, şu ifadeyi yazabiliriz:
Korelasyon, yalnızca standart hataların ikisi de sonlu ve sıfırdan farklı ise, tanımlıdır. Korelasyon katsayısının 1'i (mutlak değer olarak) geçemeyeceği ise Cauchy-Schwarz eşitsizliğinin doğal bir sonucudur.
Tam bir artan doğrusal ilişkinin varlığı halinde korelasyon katsayısı 1 değerini alır, tam bir azalan ilişkinin varlığı halinde ise korelasyon katsayısı -1 değerini alır. Katsayının alabileceği diğer tüm değerler ise ilişkinin doğrusallığına bağlı olarak bu iki değer arasında olacaktır. Katsayı +1'e veya -1'e ne kadar yakınsa ilişkinin doğrusallığı o kadar güçlüdür.
Değişkenler istatistiksel olarak bağımsız ise korelasyon 0'dır fakat bunun tersi doğru değildir, çünkü korelasyon katsayısı yalnızca doğrusal olan ilişkiyi belirler.
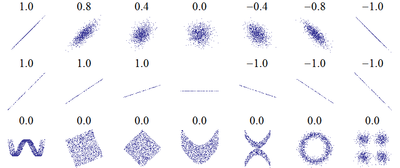
Bir örnek: Rastgele X değişkeninin -1 ve +1 aralığında tekdüze dağılımına göre dağıldığını varsayalım ve Y = X2 ilişkisi geçerli olsun. Bu durumda Y tamamen X tarafından belirlenmiştir, öyle ki X ve Y birbirlerine bağımlıdır, fakat Pearson anlamdaki korelasyon 0 olacaktır. Ne var ki, X ve Y'nin birlikte normal dağıldığı durumda, istatistiksel bağımsızlık aynı zamanda korelasyonun da olmaması anlamına gelir..
Pearson'un çarpım-moment korelasyon katsayısı örneklem kestirimi[değiştir | kaynağı değiştir]
Bir rastgele örneklem olarak n büyüklükte X ve Y değişkenleri için aralıksal ölçekli veya oransal ölçekli sayısal veri serileri bulunmaktadır ve bu seriler n satırlı ve 2 sütunlu bir veri matrisi olarak ifade edilir. Bu veriler i = 1, 2, ..., n için xi ve yi olarak yazılır. Anakütle Pearson'un çarpım-moment korelasyon katsayısı olan ρXY; için, kestirim korelasyon katsayısı olan rxy şu formül ile hesaplanır:
Burada ve xi ve yi için örneklem aritmetik ortalamaları; sx and sy xi ve yi için örneklem standart sapmaları ve toplama Σ i=1 ile n arasındadır. Bu formül biraz değişme ile şöyle de verilebilir:
Eğer X ve Y verileri normal dağılım gösteren bir anakütleden gelmişlerse, Pearson'un örneklem korelasyon katsayısı bu iki anakütle değişkeni arasında bulunan korelasyon için en iyi korelasyon kestirimi olduğu ispat edilmiştir. Yine, anakütle korelasyonu için doğru olduğu gibi, örneklem korelasyon katsayısı da -1 ile +1 arasında değişme gösterir.
Verilen formül kullanılarak, komputer kullanarak tek geçişli algoritm olarak örneklem korelasyon katsayısı hesaplanması kolay görülmesine rağmen, pratikte özellikle bu formülün kullanışı sayısal kararsız olarak pek şöhret kazanmıştır. Aşağıda daha kararlı ve kesin sonuç veren örneklem korelasyon katsayı hesaplaması verilecektir.
Örneklem korelasyon katsayısının karesi (belirtme katsayısı), xi'in yi'ye doğrusal uygunluğunun sağlanması halinde, açıklanan yi varyansı olarak da tanımlanabilir. Bu matematiksel biçimde şöyle yazılır:
Burada σy|x2 terimi xi'in yi'ye arasındaki ilişkinin bir y = a + bx doğrusu ile ifade edilmesinin kestirimi sırasında ortaya çıkan hata karelerinin toplamıdır.
ile σy2 y için varyansdır; yani
Örneklem korelasyon katsayısı hem xi'e hem yi'ya göre simetrik olduğu için, eğer bağımlı değişken olarak xi seçilip yi'in buna doğrusal uygunluğunun kestirimi elde edilirse, aynı değer
elde edilir.
Bu denklem daha yüksek boyutlarda korelasyon katsayısı bulunması için bazı ipuçları vermektedir. Yukarıda Euclid uzayı içinde bir 2-boyutlu vektör grubu için tek-boyutlu bir ölçü uygulaması halinde ortaya çıkartılan açıklanan varyans kısmı örneklem korelasyon olarak tanımlanmıştır. Aynı şekilde m boyutlu bir doğrusal alt-manifoldta n boyutlu vektörlerin uygulanması olan çoklu korelasyon katsayısı tanımlanabilir. Örneğin z için x ile y'ye göre bir düzey olan z = a + bx + cy uygulanırsa, 'z'nin x ile y'ye göre korelasyonu şöyle verilir:
Korelasyonun açıklanması[değiştir | kaynağı değiştir]
Örneklem korelasyon katsayısı iki rassal değişken olan X ve Y'yi temsil eden vektörlerin kosinus değeri olarak açıklanabilir.
Örneklem korelasyon katsayısı mümkün uçsal değerler olan -1 veya +1 olursa, çok iyi iki değişken arasında çok iyi bir doğrusal bağlantı bulunduğu kabul edilir. Eğer örneklem korelasyon katsayısı 0'a eşitse, iki değişken arasında hiç doğrusal bağlantı bulunmaz. Dikkat edilirse hep örneklem korelasyon katsayısı ile doğrusal bağlantı açıklanmakta ve genel olarak bağlantıdan bahis edilmemektedir. Örneğin iki değişken arasında çok yakın bir daire şeklinde bağlantı bulunsa, örneklem korelasyon katsayısı 0'a yakın olacaktır.
Değişik istatistikçiler örneklem korelasyon katsayısının değerlerini daha ayrıntılı olarak açıklamaktadırlar. Burada Cohen(1988),[2] tarafından, özellikle psikoloji ilim dalında uygulamalı olarak, verilen ayrıntılı açıklama şu tabloda gösterilmektedir:
| Korelasyon | Negatif | Pozitif |
| Düşük | -0,29 to -0,10 | 0,10 to 0,29 |
| Orta derecede | -0,49 to -0,30 | 0,30 to 0,49 |
| Yüksek | -0,50 to -1,00 | 0,50 to 1,00 |
Bu ayrıntılı açıklama çok subjektifdir ve belli bir bilim dalı için (psikoloji) uygundur ama genelleştirilmesi uygun değildir. Değişik bilim dalları korelasyon katsayısı değerlerinin değişik olarak açıklamasını kabul etmektedirler. Örneğin çok dakik ölçüm aletleri ile ortaya çıkarılan ölçüler arasında bulunan 0,9 korelasyon değerinin çok düşük olduğu kabul edilebilir; halbuki ayni katsayı değeri bir sosyal bilimci veya iktisatçı tarafından çok yüksek (hatta gerçekliğine şüphe yaratırcasına büyük) olarak kabul edilmektedir.
Korelasyon hakkında yaygın bazı hatalı düşünceler[değiştir | kaynağı değiştir]
Korelasyon ve nedensellik[değiştir | kaynağı değiştir]
İstatistikte korelasyon hakkında çok kullanılan ve her istatistik kullananın bilmesi gerek bir cümle şudur:
- Korelasyon veya doğrusal ilişki nedensellik değildir.
Genellikle çok kişi iki değişken arasında bir ilişki kurulunca birinin sebep diğerinin sonuç olduğuna ve birinin diğerine neden olduğuna inanmış görünürler. Gerçekten nedensellik ve korelasyon birbirine bağlı kavramlardır: nedensellik ispat edilmesi için korelasyonun bulunması gereklidir ama bu nedensellik göstermek için yeterli değildir. Nedensellik ve korelasyon birbirlerine eşit değillerdir ama daha uygun cümleler ile
- Empirik olarak gözümlenen birlikte değişme nedensellik açıklaması için gereklidir ama yeterli değildir.
- Korelasyon nedensellik değildir; ama nedenseliğin daha ayrıntılı incelenmesini gerektiren ipucunu sağlar.
İstatistikte birbiri ile çok yakından doğrusal ilişkili gibi görülen ama biri diğerine sebep-sonuç olmayan birçok pratik örnek bilinmektedir. Genellikle bu türlü nedensellikden doğmayan yakın ilişkiye sahte korelasyon adı verilmektedir. Genellikle bu sahte korelasyon iki değişkenin de bir başka saklı olan değişken tarafından etkilenmesi dolayısı ile ortaya çıkar. Biraz abstre olarak A ve B arasında bulunan yakın korelasyon daha objektif olarak dikkatle incelenince üç tür mümkün ilişki olabilceği görülür:
- A nedendir B sonuçtur;
- B nedendir A sonuçtur;
yahut
- C neden A sonuçtur VE C neden B sonuçtur.
İşte sahte korelasyon üçüncü halde ortaya çıkar. A ve B arasında görülen yakın ilişki birbirinin sebep-sonuç olmasından doğmaz. Yakın korelasyon her hâlde sebep-sonuç ilişkisi ifade etmez: "korelasyon nedensellik değildir".
Sahte korelasyon hakkında birçok örnek verilmiştir ve bunlar bazen alaycı, bazen şaşırtıcı ve bazen gülünçtür. Bunlardan bazılarını verip niçin sahte korelasyon bulunduğunu açıklayalım:
- İskandinavya'da 19. yüzyıl sonu ve 20. yüzyıl için yıllık leylek sayısı ve yıllık çocuk doğumları inceleyince çok yakın bir pozitif korelasyon bulunmaktadır. Bu, doğan çocukların leylekler tarafından getirildikleri önermesini doğrulamaz. Hem çocuk doğum sayısı hem de leylek sayısı ekonomik gelişme ve şehirleşme dolayısıyla azalmış ve bu iki azalma birinin diğerine sebep-sonuç olmasından ortaya çıkmamıştır.
- Bir sahil şehrinde aylık dondurma satışları ile aylık denizde boğulma sayıları yıl içinde birlikte artıp eksilme gösterip yakın pozitif korelasyon gösterirler. Bu demek değildir ki fazla dondurma fazla boğulmalara sebep-sonuç olmakta veya boğulmaların azalması dondurma satışlarına aksi tesirde bulunmaktadır. Her ikisi de mevsim değiştiği için aynı yönde değişik etki görmektedir.
- Ayakkabı ile uyumak, baş ağrısı ile uyanmakla yakın pozitif korelasyon gösterir. Bu demek değildir ki ayakkabı ile yatmak baş ağrısı doğurur. Çok daha uygun bir açıklama, her ikisinin de fazla alkollü içki kullanımı sonucu ortaya çıkmasıdır.
- Bir yangına müdahale eden itfaiye mensuplarının sayısı ile yangından ortaya çıkan maddi hasar birbirleri ile yakın korelasyon gösterirler. Bu demek değildir ki itfaiye mensubu sayısı artışı (yağmacı artışı gibi) daha çok maddi hasar çıkmasına neden olur. Asıl açıklama yangının büyüklüğü ve şiddetine dayanır; büyük yangınlar daha çok itfaiyeci gerektirir ve daha çok hasar doğurur.
- 1950'lerden beri hava kirliliği göstergeleri ile polise bildirilen hırsızlık olayları sayısı pozitif korelasyon göstermektedir. Bu demek değildir ki hava kirliliği artışı hırsızlık olaylarının artışına; yahut hava kirliliğinin artışı hırsızlık sayısı artışına neden olmuştur. Her iki değişkende de hızlı şehirleşme dolayısı ile artış görülmektedir.
Korelasyon ve doğrusallık[değiştir | kaynağı değiştir]

Pearson'un korelasyon katsayısı iki değişken arasındaki doğrusal ilişkinin gücünü göstermekle beraber, kestirim olarak bulunan katsayı değeri bu ilişkiyi tam olarak açıklamak için yeterli değildir. Bu sonuç eğer veriler normal dağılım göstermiyorlarsa daha da önem kazanmaktadır.
Dört değişik veri çiftini ve dört serpme diyagramını kapsayan ve istatistikçiler arasında çok iyi bilinen yandaki gösterimler İngiliz asıllı Amerikan istatistikçi Francis Anscombe tarafından hazırlanan bir yazıda gösterilmiştir.[3] Gösterilen 4 değişik y değişkeninin hepsi için de aynı olan ortalama (7,5), standart sapma (4,12), korelasyon katsayısı (0,81) ve regresyon doğrusu () bulunmaktadır. Fakat gösterimden açıkça görülmektedir ki dört Y değişkenin dağılımları çok farklıdır. Sol yukarıdaki göstergede iki değişken birbirine korelasyon ile ilişkili olup her iki değişkenin de normal dağılıma uyduğu varsayımlarının gerçeğe uygun olduğu kabul edilebilir. Üst sağdaki gösterim de değişkenlerin normal dağılım gösterdikleri kabul edilemez; iki değişken arasında ilişki olmakla beraber bunun doğrusal olduğu da kabul edilemez ve bu nedenle yüksek korelasyon katsayısı bu ilişkiyi açıklayamaz. Alt soldaki göstergeden görülmektedir ki iki değişken arasında tam bir doğrusal ilişki vardır, ancak tek bir aykırı değer bulunmakta ve bu da korelasyon katsayı değerini 1'den 0.81'e düşürmektedir. Alt sağdaki son gösterimden iki değişken arasındaki ilişkinin doğrusal olmadığı ve bulunan tek bir aykırı noktanın hesaplanan yüksek korelasyon katsayısına neden olduğu görülmektedir.
Bu örnek açıkça göstermektedir ki bir özetleme istatistiğine (burada korelasyon katsayı değerine) dayanarak, verilerin daha ayrıntılı incelenmesi yapılmadan, ortaya sonuç çıkartma iyi inceleme için gayet yetersizdir.
Korelasyon katsayısının kesin olarak tek-geçişli olarak bilgisayarla hesaplanması[değiştir | kaynağı değiştir]
Sayısal olarak kararlılığı ve kesinliği iyi olan Pearson'un çarpan-moment korelasyon katsayısı hesaplama algoritması için şu sözdekod verilmiştir:
sum_sq_x = 0
sum_sq_y = 0
sum_xy = 0
mean_x = x[1]
mean_y = y[1]
for i in 2 to N:
sweep = (i - 1.0) / i
delta_x = x[i] - mean_x
delta_y = y[i] - mean_y
sum_sq_x += delta_x * delta_x * sweep
sum_sq_y += delta_y * delta_y * sweep
sum_xy += delta_x * delta_y * sweep
mean_x += delta_x / i
mean_y += delta_y / i
pop_sd_x = sqrt(sum_sq_x / N)
pop_sd_y = sqrt(sum_sq_y / N)
cov_x_y = sum_coproduct / N
korelasyon = cov_x_y / (pop_sd_x * pop_sd_y)
Ayrıca bakınız[değiştir | kaynağı değiştir]
Kaynakça[değiştir | kaynağı değiştir]
- ^ Miles, J., & Banyard, P. (2007). Understanding and using statistics in psychology: a practical introduction. Sage.
- ^ Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.) Hillsdale, NJ: Lawrence Erlbaum Associates.
- ^ Anscombe, Francis J. (1973) Graphs in statistical analysis. American Statistician, C.27 say. 17-21.
Dış bağlantılar[değiştir | kaynağı değiştir]
- Korelasyon kavramını anlamak. Bir Hawaii Universitesi profesörü tarafından hazırlanan kılavuz 17 Aralık 2007 tarihinde Wayback Machine sitesinde arşivlendi. (en.)
- Statsoft Elektronik Ders Kitabı 16 Haziran 2008 tarihinde Wayback Machine sitesinde arşivlendi. (en.)
- Pearson'un korelasyonun katsayısının çabukca olarak hesaplanması 16 Haziran 2008 tarihinde Wayback Machine sitesinde arşivlendi. (en.)
- Korelasyon katsayısının dağılımı. Simulasyonlarla öğrenme 16 Mayıs 2008 tarihinde Wayback Machine sitesinde arşivlendi. (en.)
- İki değişken arasındaki bir doğrusal ilişkinin gücünü hesaplayan korelasyon 12 Haziran 2008 tarihinde Wayback Machine sitesinde arşivlendi. (en.)
- Bir örnek verileri için (çapraz) korelasyon katsayıları için MathWorld sayfası31 Ağustos 2019 tarihinde Wayback Machine sitesinde arşivlendi. (en.)












