Kosinüs teoremi

Vikipedi, özgür ansiklopedi

Git ve: kullan, ara
Şekil 1: Açıları ve kenarları isimlendirilmiş bir üçgen

Kosinüs teoremi, geometride, üçgen üzerinde iki kenarı ve aralarındaki açı verilmiş iken bilinmeyen kenarı bulmak amacıyla kullanılan formüldür. Şekil 1'deki üçgene göre kosinüs teoreminin uygulanışı şu şekildedir:

\ a^2 = b^2 + c^2 - 2bc \cos \alpha
\ b^2 = a^2 + c^2 - 2ac \cos \beta
\ c^2 = a^2 + b^2 - 2ab \cos \gamma

Kosinüs teoremi, iki kenar ve aralarındaki açı verildiğinde üçüncü kenarı bulmada ve üç kenar da verildiğinde açıları hesaplamada kullanılır. Ayrıca bu teorem, sadece dik üçgenlerde uygulanan Pisagor bağıntısını tüm üçgenler için geneller.

Konu başlıkları

[değiştir] İspatı

[değiştir] Uzaklık Formülüyle

Kenarları a,b,c ve c kenarının karşısındaki açısı α olan bir üçgen düşünelim. Bu üçgeni koordinat düzleminde \ A(b\cos\alpha,b\sin\alpha), B(a,0), C(0,0) noktalarıyla çizebiliriz. Buradan da uzaklık formülüyle c = \sqrt{(b\cos \alpha - a)^2+(b\sin \alpha - 0)^2} bağıntısı çıkar. Bu bağıntıdan hareketle aşağıdaki şekilde teorem ispat edilir:

\begin{align} c^2 & {} = (b\cos \alpha - a)^2+(b\sin \alpha - 0)^2 \\ c^2 & {} = b^2 \cos ^2 \alpha - 2ab\cos \alpha + a^2 + b^2\sin ^2 \alpha \\ c^2 & {} = a^2 + b^2 (\sin ^2 \alpha + \cos ^2 \alpha ) - 2ab\cos \alpha \\ c^2 & {} = a^2 + b^2 - 2ab\cos \alpha \end{align}

[değiştir] Trigonometriyle

Ana madde: Trigonometri
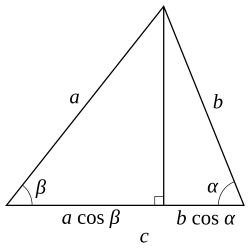
Şekil 2: Bir dikme indirilmiş üçgen

Şekil 2'deki gibi c kenarına bir dikme indirildiğinde dik üçgendeki trigonometrik bağıntılardan aşağıdaki bağıntı çıkar:

c=a\cos(\beta)+b\cos(\alpha)\,.

Her iki taraf c ile çarpıldığında ise:

c^2 = ac\cos(\beta) + bc\cos(\alpha)\,.

Aynı bağıntılar diğer kenarlara dikme indirilerek düşünülürse:

a^2 = ac\cos(\beta) + ab\cos(\gamma)\,,
b^2 = bc\cos(\alpha) + ab\cos(\gamma)\,.

bağıntıları bulunur. Her iki bağıntı alt alta toplanırsa aşağıdaki bağıntı ortaya çıkar:

a^2 + b^2 = ac\cos(\beta) + bc\cos(\alpha) + 2ab\cos(\gamma)\,

En başta verilen bağıntıyla bağlantı kurmak için:

ac\cos(\beta) + bc\cos(\alpha) = a^2 + b^2 - 2ab\cos(\gamma)\,

yapılır. Ardından en baştaki bağıntı en sondakine yazılırsa:

c^2 = a^2 + b^2 - 2ab\cos(\gamma)\,.

elde edilir.

[değiştir] İkizkenar üçgende kosinüs teoremi

Ana madde: İkizkenar üçgen

Bir ikizkenar üçgende a = b ve taban açıları eşit ve γ olduğu durumda c2 = a2 + b2 − 2abcosγ olan kosinüs teoremi aşağıdaki şekli alır:

\cos(\gamma) = 1 - \frac{c^2}{2a^2}. \;

[değiştir] İlgili konular

Trigonometri

Açı Ölçü Birimleri: Derece · Radyan · Grad
Trigonometrik işlevler: Sinüs (sin) · Kosinüs (cos) · Tanjant (tan) · Kotanjant (cot) · Sekant (sec) · Kosekant (csc)
Trigonometrik Formüller: Trigonometrik dönüşüm formülleri · Toplam fark formülleri · Kosinüs teoremi · Sinüs Teoremi · Tanjant teoremi
İlgili Konular: Üçgen · Çember · Geometri
Kullanıldığı dallar: Matematik · Geometri · Fizik · Mühendislik · Astronomi

Üçgen

Üçgen Türleri: Dik üçgen · İkizkenar üçgen · Eşkenar üçgen
Yardımcı Elemanlar: Açıortay · Kenarortay
Teoremler ve bağıntılar: Pisagor Teoremi · Seva Teoremi · Menelaus Teoremi · Steward Teoremi · Thales Teoremi · Öklid Bağıntıları · Kosinüs teoremi · Sinüs teoremi · Tanjant teoremi

"http://tr.wikipedia.org/wiki/Kosin%C3%BCs_teoremi" adresinden alındı.