Lorentz kuvveti
Bu madde, Vikipedi biçem el kitabına uygun değildir. (Şubat 2024) |
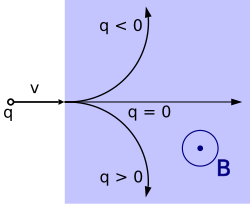
Lorentz kuvveti, fizikte, özellikle elektromanyetizmada, elektromanyetik alanların noktasal yük üzerinde oluşturduğu elektrik ve manyetik kuvvetlerin bileşkesidir. Eğer q yük içeren bir parçacık bir elektriksel E ve B manyetik alanın var olduğu bir ortamda v hızında ilerliyor ise bir kuvvet hissedecektir. Oluşturulan herhangi bir kuvvet için, bir de reaktif kuvvet vardır. Manyetik alan için reaktif kuvvet anlamlı olmayabilir, fakat her durumda dikkate alınmalıdır.
Bu temel denklemdeki farklılıklar (SI birimleri ile),[1][2] akım taşıyan teldeki manyetik alan kuvvetini tanımlamaktadır (Bazen Laplace kuvveti olarak da anılır). Manyetik alan içinde ilerleyen kapalı tel döngü üzerindeki elektromotiv kuvveti ve ışık hızında hareket eden yük taşıyan bir parçacık üzerindeki kuvveti tanımlar (Lorentz kuvvetinin relativite formudur).
Tarihçiler her ne kadar ilk çalışmaları 1865 yılında James Clerk Maxwell yazdığı bir makaleyle ilişkilendirselerde Lorenz kuvvetinin ilk geliştirilmesi, 1889 yılında Oliver Heaviside’a atfedilmektedir. Hendrik Lorentz denklemi Heaviside’dan birkaç yıl sonra geliştirmiştir.
Denklem (SI birimi)
[değiştir | kaynağı değiştir]Yüklü parçacık
[değiştir | kaynağı değiştir]
Üzerinde q yükü bulunan, dışsal E elektriksel ve B manyetik alanların etkileri nedeni ile anlık olarak v hızına sahip, bir parçacık üzerinde etkili olan F yükü aşağıdaki denklemle verilmektedir:
Burada × vektörel çarpımdır. Bütün kalın yazı fontları vektörleri göstermektedir. Daha açık olarak ifade edilirse:
Burada r, yüklü parçacığın konum vektörüdür, t zamandır ve üstel nokta zamana göre türevi ifade etmektedir.
Pozitif yüklü bir parçacık E alanının doğrusal konumu ile aynı yönde ivmelenir ancak sağ el kuralına göre hız vektörü v ve manyetik alan B’ye dik olarak eğilir (kısaca sağ el başparmağı v vektörünü gösteriyor ise ve işaret parmağı manyetik alan boyunca konuşlandırılırsa, bu durumda F vektörü yönündedir).
qE terimi elektrik kuvveti olarak, öte yandan qv × B terimi manyetik kuvvet olarak tanımlanmaktadır. Bazı tanımlara göre Lorentz kuvveti özellikle manyetik kuvvet formülüne atıfta bulunmaktadır ve toplam elektromanyetik kuvvet (elektriksel kuvvet dahil) için (standart olmayan) başka bir isim kullanmaktadır. Bu çalışma adı geçen sıra dışı sembollemeyi kullanmamaktadır.
Lorentz kuvvet'in manyetik kuvvet parçası, manyetik alan içerisinde akım taşıyan telin üzerindeki kuvvet olarak ortaya koymaktadır.
Sürekli yük dağılımı
[değiştir | kaynağı değiştir]
Hareket eylemi sırasında sürekli yük dağılımı Lorentz kuvveti için:
Burada dF dq yükü olan küçük parça için küçük bir değişimdir. Denklemin her iki tarafı da küçük parçacığın hacmi olan dV bölünürse, sonuç:
Burada f kuvvet yoğunluğudur (kuvvet/birim hacim) ve ρ yük yoğunluğu (birim hacimde). Daha sonra akım yoğunluğu yük uzayındaki harekete karşılık gelen akım yoğunluğu söyle ifade edilebilir:
Bu durumda denklemin sürekliliği ifadesi
Burada toplam güç yük dağılımı üzerinde alınacak olan hacim integrali olarak ifade edilir:
ρ ve J’yi elimine ederek, Maxwell's denklemlerini kullanarak ve vektör kalkülus teorilerini değiştirerek denklemin bu formu Maxwell stress tensör’ünü σ, ifade etmekte kullanılır, bunların sonunda Poynting vektörü S ile birleştirilerek genel görecelik kanununda kullanılan elektromanyetik stres-enerji tensörü T’nin, eldesi sağlanır.
Lorenz kuvvetini σ and S kullanarak başka şekilde yazma yöntemi (her bir 3 boyutlu hacim için)
XXXX burada c ışık hızını ∇• ıraksaklık tensörünü göstermektedir. Bu denklem enerji akısını (birim zaman ve birim mesafedeki enerji akışı), elektrik ve manyetik alandaki yük miktarı ve hız yerine, yük dağılımı ile ilişkilendirmektedir. Daha detaylı bilgi için klasik elektromagnetizma formülasyonundaki covariant formülasyonunu inceleye bilirsiniz.
Tarihçe
[değiştir | kaynağı değiştir]18. yüzyılın ortalarında elektromanyetik kuvveti tanımlama girişimleri nicel olarak başlamıştı. Johann Tobias Mayer tarafından mıknatısın kutuplarına ve başkalarına uygulanan kuvvetin ters kare kanununa uyduğu 1760 yılında ortaya atılmıştır. Aynı fikir Henry Cavendish tarafından da 1762 yılında elektriksel olarak yüklü parçacıklar için söylenmiştir. Ancak her iki durumda da deneysel kanıt ne tamamlayıcı ne de sonuç verici yöndeydi. 1748 yılında Charles-Augustin Coulomb, bir torsion tartısı kullanarak, bu teorinin doğruluğunu bir deney aracılığıyla göstererek kanıtladı.1820 yılında H. C. Ørsted manyetik iğnenin, akım tarafından etkilendiğini keşfetmesinin ardından, aynı sene André-Marie Ampère de bir deney aracılığıyla, iki akım elementi arasındaki kuvvetin açı ile olan bağlantısını açıklamayı başardı. Bütün bu tanımlarda kuvvet hep, elektrik ve manyetik alan cinsinden değil de, duruma dahil olan cisimler ve onların birbirlerine olan uzaklıkları cinsinden bulunuyordu.
Elektrik ve manyetik alanların günümüzdeki modern konsepti, ilk defa Michael Faraday tarafından ortaya atılmıştı. Bunun temellerini özellikle, daha sonra Lord Kelvin ve James Clerk Maxwell tarafından tamamen matematiksel bir tanım kazanacak olan kuvvet çizgileri fikri atmıştı. Daha modern bir bakış açısı ile Maxwell’in, alan denklemleri 1865 formülasyonlarını elektrik akımıyla ilişkilendirilmiş Lorentz kuvveti denklemi olarak da düşünebiliriz. Ancak Maxwell’in zamanında denklemlerinin, hareket eden parçacıklara etkiyen kuvvetle olan bağlantısı kanıtlanamamaktaydı. J.J. Thomson, hareket halindeki yüklü parçacıklara etkiyen elektromanyetik kuvvetleri Maxwell'in alan denklemlerini kullanarak, cismin özellikleri ve dış alanlar cinsinden türetmeye çalışan ilk insandır. Thomson 1881 yılında yüklü parçacıkların katot ışını altındaki elektromanyetik davranışlarını anlatan bir makale yazdı. Bu makalesinde parçacıklara dış bir manyetik alan sayesinde kuvvet uyguladı. Bu kuvvet ve manyetik alanın ilişkisi
Thomson neredeyse doğru olan bu temel formülü türetmeyi başarmıştı, ancak hesaplamada bir hata yapmıştı ve sürülme akımının da tanımını eksik yapmıştı. Bu sebeplerden ötürü formülün önünde olmaması gereken bir ½ bulmuştu. 1885 yılında Oliver Heaviside, vektör gösterimini bulmuş ve bunu Maxwell’in denklemlerine uygulamıştı. Aynı zamanda 1889 yılında da Thomson’un türettiği denklemdeki yanlışı düzelmiş ve hareket halinde olan parçacığa etkiyen doğru manyetik kuvveti bulmuştur. Son olarak 1892 yılında Hendrik Lorentz, kuvvete hem elektrik hem de manyetik alandan gelen katkıları da yazarak, formülün günümüzdeki modern halini türetmiştir. Lorentz, eter ve iletkenlerin Maxwellsel tanımlarından uzaklaşmaya başladı. Bunun yerine, Lorentz madde ve ışık saçan eter arasında bir ayrım belirtti. Maxwell denklemlerini de mikroskobik ölçeklerde uygulamaya karar verdi. Heaviside’ın Maxwell denklemleri versiyonunu, durgun eter üzerinde kullanarak ve buna Lagrange denklemlerini uygulayarak, kuvvet kanununun bugünkü tamamlanmış haline gelmesini ve kendi adıyla anılmasını sağladı.
Lorentz kuvveti nedeni ile parçacıkların iz düşümü
[değiştir | kaynağı değiştir]
Pek çok pratik uygulaması olan durumlar için elektrik yükü bulunan bir parçacığın (plazma içindeki elektron veya iyon) oluşturduğu manyetik alan, bir nokta etrafında (yönlendirici merkez) görece hızlı dönme hareketi ve bu noktanın yavaş kaymasının çakıştırılması olarak yapılandırılabilir. Kayma hızı, parçacık türünün yük derecesine, kütlesine veya sıcaklığına bağlı olarak değişir ve olasılıkla elektrik akımlarına ve kimyasal ayrışmalara neden olur.
Lorentz kuvvetlerinin önemi
[değiştir | kaynağı değiştir]Modern Maxwell denklemleri elektrik yükü taşıyan parçacıkların ve akımların veya yüklü parçacıkların hareketinin, elektrik ve manyetik alanı nasıl oluşturduğunu tanımlarken, Lorentz kuvveti kanunu elektromanyetik alanın hareket eden yüklü parçacığın üzerinde yarattığı kuvveti tanımlayarak, resmi tamamlamaktadır. Lorentz kuvveti E ve B’nin yüklü bir parçacık üzerindeki etkisini tanımlamaktadır. Ancak bu elektromanyetik kuvvetler bütün resmi kapsamamaktadır. Yüklü parçacılar, muhtemelen yerçekimi ve nükleer kuvvetler gibi diğer kuvvetlerle eşleşmişlerdir. Bu nedenle Maxwell denklemleri diğer fizik kanunlarında ayrı tutulamaz ve yük ve akım yoğunlukları vasıtası ile ilişkilendirilmişlerdir. Nokta yükün Lorentz kanununa verdiği tepki işin bir yönü iken, E ve B’nin akımlar ve yükle nedeni ile oluşması diğer yönüdür.
Gerçek malzemelerde Lorentz kuvveti yüklü parçacıkların davranışını tanımlamakta, hem prensip olarak hem de hesaplama olarak yetersiz kalmaktadır. Bir malzeme ortamında, yüklü parçacıklar hem E’ye hem de B’ye tepki verirler ve ayrıca bu alanları oluştururlar. Karmaşık taşınım denklemleri yüklerin zaman ve uzaydaki tepkilerini belirlemek için çözülmelidir. Örneğin, Boltzman denklemi, Fokker-Planck denklemi veya Navier-Stokes denklemi gibi. Magnetohidrodinamik, akışkanlar dinamiği, elektrohidrodinamik, süper-iletkenlik, yıldız oluşumu gibi konular incelenebilir. Bu konuları irdeleyecek fizik donanımları (kanunlar, denklemler ve matematik vb..) geliştirilmiştir. Bu amaçla Green-Kubo ilişkileri ve Green denklemleri (çoklu gövde teorisi) incelenebilir.
E ve B’nin tanımlamasında Lorentz kuvveti
[değiştir | kaynağı değiştir]Pek çok kitabın klasik elektromanyetik bölümünde Lorentz kanunu elektrik E ve manyetik B alanları tanımlamakta kullanılır. Daha spesifik bir tanımlama ile Lorentz kuvveti aşağıdaki dogma olarak algılanır: Bir test yükü için elektromanyetik güç, F, tanımlı bir noktada ve zamanda taşıdığı yüke ve hızına bağlıdır. Bu iki faktör tam olarak, E ve B’nin, iki vektörü ile parametreleşir. Bu yapın fonksiyonel formu:
Bu dogma sayısız deneylerle gösterilmiştir. Hatta ışık hızına yaklaşan parçacıklar (v = |v| = c) için de geçerlidir. Bu durumda uzay ve zamanda verilen iki vektör alanı E ve B, elektrik alanı ve manyetik alan olarak tanımlanmıştır. Bu iki alan bütün uzay ve zamanda test yüküne bağlı olarak tanımlanmıştır ve söz konusu kuvvetten etkilenecek bir bir yükün olup olmamasında bağımsız olarak geçerlidir. Ayrıca, E ve B’nin tanımında Lorentz kuvveti tek prensiptir. Çünkü, varsayımsal sonsuz küçük kütle ve yüke sahip “test yükünün” aksine gerçek bir parçacık kendi sınırlı E ve B’sini yaratır ve etkilendiği elektromanyetik kuvveti değiştirir. İlave olarak, yük bir dış etkileyici tarafından ivmelendirilerek kavisli bir yola zorlanırsa, hareketini frenleyen bir radyasyon yayar. Bunun örnekleri olarak Bremsstrahlung ve synchrotron light kavramları incelenebilir. Bu etkiler doğrudan (radyasyon reaksiyon kuvveti) ve dolaylı etkilerin (etrafındaki yük ve akımları etkilemesi) sonucudur. Dahası sonuç kuvveti elektromanyetik kuvvetin yanı sıra yerçekimini, elektro zayıflığı ve diğer kuvvetleri de içermelidir.
Akım taşıyan teldeki kuvvet
[değiştir | kaynağı değiştir]
Akım taşıyan bir tel manyetik bir alan içine yerleştirildiğinde, hareket eden, akımı taşıyan her bir yük Lorents kuvvetinden etkilenir ve tel üzerinde, bazen Laplace kuvveti olarak da adlandırılan, makroskopik büyüklükte bir kuvvet oluşturur. Yukarıda tanımı verilmiş olan Lorentz kuvveti kanununu elektrik akımı kavramı ile birleştirince düz ve hareketsiz tel için aşağıdaki denklem elde edilir:
Burada ℓ, büyüklüğü telin uzunluğu ve yönü tel boyunca olan, konvansiyonel akım, I, yönünde hizalanmış vektördür. Telin doğrusal değil de kavisli olması durumunda, kuvvet, telin küçük parçaları dℓ,için hesaplanır ve sonra bütün kuvvetlerin integrasyonla toplanması ile bulunur. Sabit akım,,, taşıyan düz sağlam bir tel üzerindeki net kuvvet:
Bu net kuvvettir. Telin mükemmel katı cisim olmaması durumunda, ilave olarak moment ve diğer etkiler olacaktır. Bunun bir uygulaması Ampere’in kuvvet kanunudur. Akım taşıyan iki telin, diğerinin manyetik alanı nedeni ile oluşan Lorentz kuvvetlerine bağlı olarak birbirlerini nasıl çektiklerini veya ittiklerini tanımlar. Detaylı bilgi “Ampere’in kuvvet kanunu’ndan” incelenebilir.
EMF
[değiştir | kaynağı değiştir]Lorentz kuvvetinin manyetik bileşeni olan (q v × B), hareketsel elektromotif kuvvetten sorumludur. Bu kuvvet de elektrik motorlarının altında yatan temel fenomendir. Bir iletken, manyetik alanın içinde hareket ettirildiği zaman, manyetik kuvvet elektronu tel içerisinde ittirmeye çalışır ve bu da bir EMF oluşturur. “Hareketsel EMF” kavramı da bu fenomene uygulanabilir çünkü EMF de telin hareketine bağlı olarak oluşur. Başka elektriksel motorlarda da, mıknatıs hareket eder, iletkenler etmez. Bu durumda, EMF Lorentz denklemindeki (qE) terimine bağlı olur. Bu durumda elektrik alan değişen manyetik alan sayesinde oluşur ve bu elektrik alan da Maxwell-Faraday denklemlerinde belirtilen bir indüklenmiş EMFe sebep olur.
Farklı kaynaklardan doğmalarına rağmen bu iki EMF de aynı denklem ile açıklanabilir, çünkü EMF teldeki manyetik akıda oluşan değişime tekabül eder. (Bu Faraday’ın Kanunudur.) Einstein’in özel görelilik teorisi de kısmen bu iki etki arasındaki bağı daha iyi anlamaktan esinlenerek yola çıkılmıştır. Hatta, hem elektrik hem manyetik alan, ikisi de aynı elektromanyetik alanın iki farklı yüzüdürler ve bir eylemsiz referans sisteminden, diğerine geçiş yaparlar. Yani elektrik alanın solenoid vektör alan kısmı tamamen manyetik alana dönüşebilir ya da manyetik alan için tam tersi.
Lorentz kuvveti ve Faraday’ın indüksiyon kanunu
[değiştir | kaynağı değiştir]Manyetik alanın içinde bir tel verildiğinde, Faraday’ın indüksiyon kanunu, teldeki EMF’nin bu olduğunu belirtir:
burada
Manyetik akı, B manyetik alan, Σ(t) sınırları belirtilmiş (∂Σ(t)) olan yüzey, t kadar bir sürede, dA ise küçük vektör alanı olmaktadır. EMF’ nin işareti de Lenz Kanunu ile belirlenir. Bu hem hareket halinde olan tel hem de durgun haldeki tel için geçerlidir. Faraday’ın indüksiyon kanunundan ve Maxwell denklemlerinden Lorentz Kuvveti anlaşılabilir. Aynı şekilde tam tersi olarak, Lorentz Kuvvetinden de Maxwell denklemleri ve Faraday Kanununa ulaşılabilir. Σ(t) hareket halindeki, dönme hareketi yapmayan, sabit v hızıyla hareket eden tel olsun ve Σ(t) de telin iç yüzey alanı olsun. Kapalı bir yol üzerindeki EMF ∂Σ(t):
burada
Elektrik alan ve dℓ ise ∂Σ(t) ile sınırları belirlenmiş ve ifade edilen küçük vektör elementi olmaktadır. NB: Hem dℓ ‘in hem de dA’nın işareti belirsizdir; doğru işareti belirleyebilmek için, Kelvin-Stokes teoremi makalesinde de açıklandığı gibi sağ el kuralı kullanılır. Yukarıdaki sonuç, Faraday’ın indüksiyon kanununda çıkan versiyon ve modern Maxwell denklemleriyle de kıyaslanabilir. Burada Maxwell-Faraday denklemi olarak verilmiştir:
Maxwell-Faraday denklemi integral kullanılarak da Kevin-Stokes teoremi aracılığıyla yazılabilir:. Böylece elimizde Maxwell-Faraday denklemi oluşur:
Ve Faraday Kanunu,
Bu ikisi eğer tel hareket halinde değil ise birbirine eşittir. Leibniz integral kuralını ve div B = 0’ı kullanarak,
elde edebiliriz Ve Maxwell Faraday denklemini kullanırsak,
Bu her hangi pozisyondaki tel için geçerli olduğu için şunu belirtir,
Faraday’ın indüksiyon kanunu telin düzgün ve hareketsiz olup olmamasına ya da hareket halinde olup olmamasına ya da deformasyon aşamasında olup olmadığına bakmaksızın geçerlidir. Ayrıca manyetik alanın sabit veya değişken olmasına da bağlı değildir. Ancak bazı durumlarda Lenz yasasını kullanmanın yetersiz veya zor olduğu durumlar vardır. Bu durumlarda Lorentz kuvveti yasasını kullanmak gereklidir.
Eğer belirli bir zaman boyunca manyetik alan sabitse ve iletken tel manyetik alan içinde hareket ediyorsa, manyetik akı birçok şekilde değişebilir. Örneğin, eğer manyetik alan yere göre değişiyorsa ve tel farklı bir manyetik alanın etkisi altına girecek bir yere gidiyorsa, akı değişir. Buna alternatif olarak eğer tel manyetik alana göre oryantasyon değiştiriyorsa, B • dA diferansiyel elemanı da değişecektir, çünkü B ve dA arasındaki açı da değişecektir. Aynı zamanda akı da değişecektir. Üçüncü bir örnek olarak da, eğer devrenin belirli bir kısmı zamandan bağımsız, düzgün bir manyetik alandan geçiriliyorsa ve bir diğer kısmı da sabit tutuluyorsa, bütün kapalı devreyi bağlayan, göreceli kısımlardaki zaman içindeki değişim sebebiyle bir akı değişimi olabilir. Bu üç durumda da Faraday’ın indüksiyon kanunu, manyetik akı değişimi sebebiyle bir EMF oluşacağı yorumunu yapmamıza yardımcı oluyor.
Ayrıca Maxwell Faraday denklemi, manyetik alanın zamana bağlı olarak değiştiği yerlerde, elektrik alanın korunumlu olmadığını ve bu sebeple skaler alanın gradyeni olarak ifade edilemeyeceğini ve de, dönmesi sıfır olmadığından dolayı gradyen teoremine tabi tutulamayacağını söyler.
Potansiyel türünden Lorentz kuvveti
[değiştir | kaynağı değiştir]E ve B alanları manyetik vektör potansiyeli A ve skaler elektrostatik potansiyel ϕ ile yer değiştirerek de ifade edilebilir.
burada ∇ gradyen, ∇• gradyen diverjansı, ∇ × ise kıvrımdır. Böylece kuvvet bu hale gelir
Ve bu da, üçlü çarpımı basite indirgemek için bir yöntem kullanılarak
zincir kuralı kullanılarak, A’nın total türevi:
olur. böylece yukarıdaki ifade;
bu şekilde de yazılabilir. bu da kullanışlı olan Euler-Lagrange formunu alabilir.
Lorentz kuvveti ve analitik mekaniği
[değiştir | kaynağı değiştir]Kütlesi m ve yükü q olan elektromanyetik alanda olan bir parçacığın Lagranjiyanı onun, uygulanan kuvvetten ziyade, enerji türünden dinamiğini açıklar. Klasik ifade edilme yöntemi:
Burada A ve ϕ yukarıdaki potansiyel alanlardır. Lagrange denklemlerini kullanarak, Lorentz denklemini elde edebiliriz.
Klasik Lgranjiyandan Lorentz kuvvetinin türetilmesi (SI birimleri) Bir A alanı için v = ṙ hızıyla hareket eden bir parçacık potansiyel momentuma sahiptir: , yani potansiyel enerjisi olur. Potansiyel enerji parçacığın hızına bağlıdır, yani kuvvet hıza bağlıdır, yani korunumlu değildir. Gerçekçi Lagranjiyan ise
Buradaki detay ise parçacığın uzay-zamanında, yolunun gerçekçi yay uzunluğuna sahip olması, potansiyel enerjiden fazladan bir katkı gelmiyor olması, ayrıca yüklü bir parçacığın vektör potansiyelinde hareket ederken kazandığı fazladan bir haldir.
Lorentz kuvvetinin göreceli Lagrangian'dan (SI birimleri) türetilmesi Eylemin ekstremizasyon tarafından türetilen hareket denklemleri (gösterim için matris hesabına bakın):
Denklem (cgs birimleri)
[değiştir | kaynağı değiştir]Yukarıda belirtilen formüllerde SI birimleri kullanılmaktadır. Sı birimleri deneyciler, teknisyenler ve mühendisler arasında en yaygın olarak kullanılan birimlerdir. Cgs-Gauss birimlerinde ise, teorik fizikçiler arasında daha yaygındır. Bu birim kullanıldığında
Burada c ışık hızıdır. Bu denklem biraz daha farklıymış gibi görünse bile, bire bir aynı denklemlerdir. SI ve cgs birimleri arasında şu gibi geçişler vardır:
Burada ε0 boşluğun elektrik geçirgenliğidir ve μ0 ise boşluğun geçirgenliğidir. Uygulamada “cgs” ve “SI” için kullanılan simgeler dahil edilmezler ve bu birimler içerikten yola çıkılarak tahmin edilmelidir.
Lorentz kuvvetinin görecelilik formunda ifadesi
[değiştir | kaynağı değiştir]Lorentz kuvveti, bir yük için, metrik notasyon kullanılarak (-1,1,1,1) kovaryant formunda (ortak değişken formunda) aşağıdaki gibi yazılabilir:
burada pα dört-momentumdur. Bu şu şekilde tanımlanmıştır:
parçacığın uygun zamanı, Fαβ de kontravaryantın elektromanyetik tensörüdür.
ve U ‘da aşağıdaki gibi tanımlanmış olan dört-hız kovaryantıdır:
burada yukarıda tanımlamış olan Lorentz faktörüdür. Alanlar sabit görece bir hızda hareket eden bir sınıra dönüştürülmüştür:
burada Λμα Lorentz dönüşüm tensörüdür.
Vektör notasyonuna dönüşümü
[değiştir | kaynağı değiştir]Kuvvetin tanımlı α = 1 bileşeni (x-bileşeni)
Kovaryant elektromanyetik tensör bileşenleri yerine konursa, F denklemi aşağıdaki forma dönüşür:
Kovaryant dört-hız bileşeni kullanılarak denklem:
α = 2, 3 (y ve z yönündeki kuvvet bileşenleri) için yapılan hesaplamalar benzer sonuçlar ortaya koyar, böylece 3 denklemi birleştirilmesi ile:
Lorentz kuvveti ortaya çıkar.
Lorentz kuvvetinin STA formu
[değiştir | kaynağı değiştir]Elektrik ve manyetik alanlar gözlemcinin hızı ile ilişkilidir, bu nedenle Lorentz kuvvetinin görecelilik formu en uygun olarak, rastgele seçilmiş bir zaman yönünde,, elektromanyetik ve manyetik alanların,, koordinattan arındırılmış ifadesi ile sağlanır:
ve
uzay-zaman çift-vektörü (bir doğru parçasına yerleştirilmiş vektör gibi, konuşlandırılmış düzlem parçası), itmelere (uzay-zaman düzleminde dönmeler) ve dönmelere (uzay-uzay düzlemlerinde dönmeler) karşılık gelen altı adet serbestlik derecesi vardır. vektörü ile iç-çarpım dönüşümsel gruptan bir vektör (uzay cebirinde) oluştururken, vektörel çarpım, genellikle manyetik alan vektörü olan bir vektör ile eşleşmiş bir üçlü bir vektör oluşturur (uzay cebirinde). Görece-hız, zaman – konum vektöründe,, (zaman benzeri) bir değişimle verilir;
(metrik tercihi gösteren) ve hız ifadesi:
Lorentz kuvvetinin uygun (herhangi bir değişim tanımlanmadığı için değişimsiz tanımı yetersiz kalmaktadır) formu sadeleştirilmiş olarak:
Çift vektör ve vektör arasında içsel çarpım ters bakışımlı (anti symmetric) olduğu için burada derecenin önemli olduğuna dikkat çekmek gerekmektedir. Uzay zaman ayrışmasına bağlı olarak hızın elde edilmesi gibi alanlarda bilinen tanımlamayı ortaya koymaktalar.
Uygulamaları
[değiştir | kaynağı değiştir]Lorentz kuvveti, aşağıdaki örneklerde dahil olmak üzere pek çok cihazda oluşur:
- Sıkletron ve diğer dairesel parçacık hızlandırıcılar.
- Kütle spektroskopları
- Hız filtreleri
- Magnetronslar
- Lorentz kuvveti hız ölçerleri; Bir iletkendeki Laplace kuvveti olarak oluşmasına bağlı olarak bu kuvvet pek çok cihazda görülür.
- Elektrik motorları
- Yataklı atış sistemleri
- Doğrusal motorlar
- Hoparlörler • Magnetoplasmadinamik yükleyiciler
- Elektrik jeneratörleri
- Tek kutuplu jeneratörler
- Doğrusal alternatörler
Ayrıca bakınız
[değiştir | kaynağı değiştir]- Hall etkisi
- Elektromagnetizma
- Hendrik Lorentz
- Maxwell denklemleri
- Abraham-Lorentz kuvveti
- Larmor formülü
Kaynakça
[değiştir | kaynağı değiştir]- ^ SI birimlerinde, B, tesla cinsinden ölçülür (sembol: T). Gauss-cgs birimleri cinsinden, B, gauss (sembol: G) cinsinden ölçülür. "Geomagnetism Frequently Asked Questions". National Geophysical Data Center. 8 Temmuz 2018 tarihinde kaynağından arşivlendi. Erişim tarihi: 21 Ekim 2013.)
- ^ H-alanı, SI birimlerinde metre başına amper (A/m) cinsinden ve cgs birimlerinde Oersteds (Oe) cinsinden ölçülür. "International system of units (SI)". NIST reference on constants, units, and uncertainty. National Institute of Standards and Technology. 12 Nisan 2010. 19 Ocak 2017 tarihinde kaynağından arşivlendi. Erişim tarihi: 9 Mayıs 2012.
- Feynman, Richard Phillips; Leighton, Robert B.; Sands, Matthew L. (2006). The Feynman lectures on physics (3 vol.). Pearson / Addison-Wesley. ISBN 0-8053-9047-2.: volume 2.
- Griffiths, David J. (1999). Introduction to electrodynamics (3rd ed.). Upper Saddle River, [NJ.]: Prentice-Hall. ISBN 0-13-805326-X.
- Jackson, John David (1999). Classical electrodynamics (3rd ed.). New York, [NY.]: Wiley. ISBN 0-471-30932-X.
- Serway, Raymond A.; Jewett, John W., Jr. (2004). Physics for scientists and engineers, with modern physics. Belmont, [CA.]: Thomson Brooks/Cole. ISBN 0-534-40846-X.
- Srednicki, Mark A. (2007). Quantum field theory. Cambridge, [England] ; New York [NY.]: Cambridge University Press. ISBN 978-0-521-86449-7.
Dış bağlantılar
[değiştir | kaynağı değiştir]- Lorentz kuvveti (gösteri)
- Homojen bir manyetik alanda bir parçacık ışınının manyetik sapmasına ilişkin etkileşimli Java uygulaması 13 Ağustos 2011 tarihinde Wayback Machine sitesinde arşivlendi. Wolfgang Bauer.


![{\displaystyle \mathbf {F} (\mathbf {r} ,\mathbf {\dot {r}} ,t,q)=q[\mathbf {E} (\mathbf {r} ,t)+\mathbf {\dot {r}} \times \mathbf {B} (\mathbf {r} ,t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09e1b5355b1ba774c429c04f7422db91a34ae831)






















![{\displaystyle \mathbf {F} =q\left[-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}+\mathbf {v} \times (\nabla \times \mathbf {A} )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91a8cb8954da8ad9451ab18ed4b0fdc3a15ac32e)
![{\displaystyle \mathbf {F} =q\left[-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}+\nabla (\mathbf {v} \cdot \mathbf {A} )-(\mathbf {v} \cdot \nabla )\mathbf {A} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7fd3adddbdfb95797d11ef6167ecda4efe3e0b9)

![{\displaystyle \mathbf {F} =q\left[-\nabla (\phi -\mathbf {v} \cdot \mathbf {A} )-{\frac {d\mathbf {A} }{\mathrm {d} t}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80711365244060be993f180b7af7b437d56fc868)
![{\displaystyle \mathbf {F} =q\left[-\nabla _{\mathbf {x} }(\phi -{\dot {\mathbf {x} }}\cdot \mathbf {A} )+{\frac {\mathrm {d} }{\mathrm {d} t}}\nabla _{\dot {\mathbf {x} }}(\phi -{\dot {\mathbf {x} }}\cdot \mathbf {A} )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9949c2ff8130b2afa9bc01498342a043eda8540)













![{\displaystyle {\frac {\mathrm {d} p^{1}}{\mathrm {d} \tau }}=q\left[U_{0}\left({\frac {-E_{x}}{c}}\right)+U_{2}(B_{z})+U_{3}(-B_{y})\right].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1098be24dfbd6135201022a5a8055992fd616b07)
![{\displaystyle {\begin{aligned}{\frac {\mathrm {d} p^{1}}{\mathrm {d} \tau }}&=q\gamma \left[-c\left({\frac {-E_{x}}{c}}\right)+u_{y}B_{z}+u_{z}(-B_{y})\right]\\&=q\gamma \left(E_{x}+u_{y}B_{z}-u_{z}B_{y}\right)\\&=q\gamma \left[E_{x}+\left(\mathbf {u} \times \mathbf {B} \right)_{x}\right]\,.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0af03e1e2595b9ab322e16e2b8611d3179674155)





