Açısal çap
Açısal çap, açısal boyut, görünür çap veya görünür boyut, bir küre veya dairenin belirli bir bakış açısından ne kadar büyük göründüğünü tanımlayan açısal mesafedir. Görme bilimlerinde buna görüş açısı, optikte ise (bir merceğin) açısal açıklığı denir. Alternatif olarak açısal çap bir gözün veya kameranın, görünen bir dairenin bir tarafından diğer tarafına bakabilmek için dönmesi gereken açısal yer değiştirme olarak da düşünülebilir. İnsanlar çıplak gözleriyle yaklaşık 1 yay-dakika (yaklaşık 0,017° veya 0,0003 radyan) çapa kadar çözünürlük elde edebilirler.[1] Bu, 1 km mesafede 0,3 m'ye ya da en uygun koşullarda Venüs'ün bir disk olarak algılanmasına karşılık gelir.
Formül[değiştir | kaynağı değiştir]

Bakış noktası ile dairenin merkezi arasındaki yer değiştirme vektörüne dik olan düzlemdeki bir dairenin açısal çapı, aşağıdaki formül kullanılarak hesaplanabilir:[2]
Burada "derece" cinsinden açısal çap, nesnenin gerçek çapı ve nesneye olan mesafedir. olduğunda, olur ve elde edilen sonuç radyan cinsindendir.
Gerçek çapı 'a eşit olan ve 'nin kürenin merkezine olan mesafesi olduğu küresel bir nesne için açısal çap aşağıdaki formülle bulunabilir:
Aradaki fark, bir kürenin görünen kenarlarının, gözlemciye kürenin merkezinden daha yakın olan teğet noktaları olduğu gerçeğinden kaynaklanır. Aşağıdaki küçük açı yaklaşımları 'in küçük değerleri için geçerli olduğundan, fark yalnızca büyük açısal çapa sahip küresel nesneler için önemlidir:[3]
El kullanılarak açısal çap tahmini[değiştir | kaynağı değiştir]

Açısal çap tahminleri, şekilde gösterildiği gibi elin tamamen uzatılmış bir kola dik açıda tutulmasıyla elde edilebilir.[4][5]
Astronomide kullanım[değiştir | kaynağı değiştir]
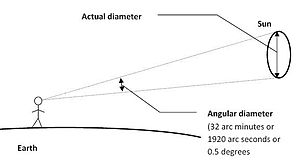
Astronomide, gök cisimlerinin boyutları genellikle gerçek fiziksel boyutlarından ziyade Dünya'dan görüldükleri açısal çaplarıyla ifade edilir. Bu açısal çaplar tipik olarak küçük olduğundan, bunların yay-saniye (″) cinsinden sunulması yaygındır. Bir yay- saniye, bir derecenin (1°) 1/3600'üdür ve bir radyan 180/π derecedir. Yani bir radyan, 3.600 × 180/ yay-saniyeye eşittir, bu da yaklaşık 206.265 yay-saniyedir (1 rad ≈ 206.264,806247"). Bu nedenle, fiziksel çapı d olan bir cismin D mesafesindeki açısal çapı yay-saniye (arcsecond) cinsinden ifade edildiğinde, şu formülle hesaplanır:[6]
- .
Aşağıdaki nesnelerin açısal çapı 1 yay-saniyedir:
- 2,06 km mesafede 1 cm çapında bir nesne
- 1 astronomik birim (AU) mesafede 725,27 km çapında bir nesne
- 1 ışık yılı mesafede 45.866.916 km çapında bir nesne
- 1 parsek (pc) mesafede 1 AU (149.597.871 km) çapında bir nesne
Bu nedenle, Dünya'nın yörüngesinin ortalama yarıçapı 1 AU olduğundan, 1 pc mesafeden bakıldığında Dünya'nın Güneş etrafındaki yörüngesinin açısal çapı 2 yay-saniyedir.
Bir ışık yılı mesafeden Güneş'in açısal çapı 0,03″, Dünya'nınki ise 0,0003″'tür. Güneş'in 0,03″ açısal çapı, Dünya'nın çapı kadar mesafedeki bir insan vücudunun açısal çapıyla yaklaşık olarak aynıdır.
Aşağıdaki tablo, Dünya'dan görüldüğü şekliyle kayda değer gök cisimlerinin açısal boyutlarını göstermektedir:
| Gök cismi | Açısal çap veya boyut | Göreli boyut |
|---|---|---|
| Magellan Akıntısı | 100°'den fazla | |
| Gum Bulutsusu | 36° | |
| Samanyolu | 30° (360°'ye kadar) | |
| Uzatılmış kol ile açılmış el genişliği | 20° | 1 km mesafeden 353 metre |
| Yılan-Kartal Yarığı | 20° × 10° | |
| Büyük Köpek Cüce Gökadası | 12° × 12° | |
| Smith'in Bulutu | 11° | |
| Büyük Macellan Bulutu | 10,75° × 9,17° | Not: Samanyolu dışında gece gökyüzündeki en parlak gökada (0,9 kadir (V)) |
| Barnard İlmiği | 10° | |
| Zeta Ophiuchi Sh2-27 bulutsusu | 10° | |
| Kol uzatılmış haldeyken yumruk genişliği | 10° | 1 km mesafeden 175 metre |
| Yay Eliptik Cüce Galaksisi | 7.5° × 3.6° | |
| Büyük Yarık Kuzey Kömür Çuvalı Bulutsusu |
7° × 5°[7] | |
| Kömür Çuvalı Bulutsusu | 7° × 5° | |
| Cygnus OB7 | 4° × 7°[8] | |
| Rho Ophiuchi bulut kompleksi | 4.5° × 6.5° | |
| Hyades | 5°30′ | Not: Gece gökyüzündeki en parlak yıldız kümesi, 0,5 kadir (V) |
| Küçük Macellan Bulutu | 5°20′ × 3°5′ | |
| Andromeda Gökadası | 3°10′ × 1° | Güneş ya da Ay'ın yaklaşık altı katı büyüklüğündedir. Uzun pozlama olmadan sadece çok daha küçük olan çekirdek görülebilir. |
| Charon (Plüton'un yüzeyinden) | 3°9’ | |
| Peçe Bulutsusu | 3° | |
| Kalp Bulutsusu | 2,5° × 2,5° | |
| Ruh Bulutsusu | 2,3° × 1,25° | |
| Sh2-54 | 2,3° | |
| Karina Bulutsusu | 2° × 2° | Not: Gece gökyüzündeki en parlak bulutsu, 1,0 kadir (V) |
| Kuzey Amerika Bulutsusu | 2° × 100′ | |
| Ay'ın gökyüzünde Dünya | 2° - 1°48′[9] | Dünya gökyüzündeki Ay'dan yaklaşık üç ila dört kat daha büyük görünür |
| Orion Bulutsusu | 1°5′ × 1° | |
| Kol uzatıldığında küçük parmak genişliği | 1° | 1 km mesafeden 17,5 metre |
| Io (Jüpiter'in "yüzeyinden" görüldüğü gibi) | 35’ 35” | |
| Ay | 34′6″ – 29′20″ | Venüs için maksimum değerin 32,5-28 katı (aşağıdaki turuncu çubuk) / 2046-1760″ Ay'ın çapı 3.474 km'dir |
| Güneş | 32′32″ – 31′27″ | Venüs için maksimum değerin 31-30 katı (aşağıdaki turuncu çubuk) / 1952-1887″ Güneş'in çapı 1.391.400 km'dir |
| Triton (Neptün'ün "yüzeyinden") | 28’ 11” | |
| Alt kavuşma konumunda Mars'tan bakıldığında Dünya ile Ay arasındaki mesafenin açısal boyutu. | yaklaşık 25′ | |
| Ariel (Uranüs'ün "yüzeyinden") | 24’ 11” | |
| Ganymede (Jüpiter'in "yüzeyinden") | 18’ 6” | |
| Europa (Jüpiter'in "yüzeyinden") | 17’ 51” | |
| Umbriel (Uranüs'ün "yüzeyinden") | 16’ 42” | |
| Helis Bulutsusu | yaklaşık 16′ × 28′ | |
| Kartal Bulutsusu'ndaki kule | 4′40″ | uzunluğu 280″ |
| Venüs | 1′6″ – 0′9,7″ | |
| Uluslararası Uzay İstasyonu (ISS) | 1′3″ | [10] ISS yaklaşık 108 m genişliğe sahiptir |
| İnsan gözü tarafından çözülebilen minimum çap | 1′ | [11] 1 km mesafeden 0,3 metre[12] |
| Ay yüzeyinde yaklaşık 100 km | 1′ | Kopernik krateri gibi büyük Ay kraterleri, Oceanus Procellarum'un alçalan tarafındaki doğu kısmında belirgin bir parlak nokta veya Ay'ın yakın yüzünün güneyindeki parlak bir alan içindeki Tycho krateri gibi özelliklerin boyutuyla karşılaştırılabilir. |
| Jüpiter | 50,1″ – 29,8″ | |
| İki çizgi arasında insan gözünün çözebileceği minimum boşluk | 40″ | 15 cm uzaklıktan bakıldığında 0,026 mm'lik bir boşluk[11][12] |
| Mars | 25,1″ – 3,5″ | |
| Günötede 90377 Sedna'dan görülen Güneş'in görünür büyüklüğü | 20,4" | |
| Satürn | 20,1″ – 14,5″ | |
| Merkür | 13,0″ – 4,5″ | |
| Uranüs | 4,1″ – 3,3″ | |
| Neptün | 2,4″ – 2,2″ | |
| Ganymede | 1,8″ – 1,2″ | Ganymede'nin çapı 5.268 km'dir. |
| ISS'nin ortalama yüksekliği olan 350 km uzaklıktaki bir astronot (~1,7 m) | 1″ | |
| Galileo Galilei'nin en büyük 38 mm'lik kırılmalı teleskopları tarafından çözülebilen minimum çap | ~1″ | [13] Not: 30x[14] büyütme, çok güçlü çağdaş karasal dürbünlerle karşılaştırılabilir |
| Ceres | 0,84″ – 0,33″ | |
| Vesta | 0,64″ – 0,20″ | |
| Plüton | 0,11″ – 0,06″ | |
| Eris | 0,089″ – 0,034″ | |
| R Doradus | 0,062″ – 0,052″ | Not: R Doradus'un Dünya'dan bakıldığında en büyük görünür boyuta sahip güneş dışı yıldız olduğu düşünülmektedir |
| Betelgeuse | 0,060″ – 0,049″ | |
| Alphard | 0,00909″ | |
| Rho Cassiopeiae | 0,0072″ | |
| Alfa Centauri A | 0,007″ | |
| Canopus | 0,006″ | |
| Sirius | 0,005936″ | |
| Altair | 0,003″ | |
| Deneb | 0,002″ | |
| Proxima Centauri | 0,001″ | |
| Alnitak | 0,0005″ | |
| Proxima Centauri b | 0,00008″ | |
| M87 gökadasının merkezindeki M87* kara deliğinin olay ufku, 2019'da Olay Ufku Teleskobu tarafından görüntülendi. | 0,000025″
(2,5×10-5) |
Ay'daki bir tenis topuyla karşılaştırılabilir |
| Alnitak gibi bir yıldız, Hubble Uzay Teleskobu'nun onu görmekte güçlük çekeceği bir mesafede.[15] | 6×10-10 yay-saniye |



Güneş'in Dünya'dan görülen açısal çapı Sirius'unkinin yaklaşık 250.000 katıdır. (Sirius'un çapı iki kattır ve mesafesi 500.000 kat daha fazladır; Güneş 1010 kat daha parlaktır, bu da 105 açısal çap oranına karşılık gelir, yani Sirius tam açı birim başına kabaca 6 kat daha parlaktır.)
Güneş'in açısal çapı, ayrıca Alfa Centauri A'nın açısal çapının yaklaşık 250.000 katıdır (yaklaşık aynı çapa sahiptir ve uzaklığı 250.000 kat daha fazladır; Güneş 4×1010 kat daha parlaktır, bu da 200.000 açısal çap oranına karşılık gelir) yani Alfa Centauri A tam açı birim başına biraz daha parlaktır).
Güneş'in açısal çapı, Ay'ın açısal çapıyla yaklaşık olarak aynıdır. (Güneş'in çapı 400 kat daha büyüktür ve ayrıca mesafesi de; Güneş, dolunaydan 200.000 ila 500.000 kat daha parlaktır (rakamlar değişir), bu da 450 ila 700'lük bir açısal çap oranına karşılık gelir, bu nedenle 2,5–4″ çapında ve tam açı birim başına aynı parlaklığa sahip bir gök cismi, dolunay ile aynı parlaklığa sahip olacaktır).
Plüton fiziksel olarak Ceres'ten daha büyük olsa da, Dünya'dan bakıldığında (örneğin, Hubble Uzay Teleskobu aracılığıyla) Ceres çok daha büyük bir görünür boyuta sahiptir.
Derece cinsinden ölçülen açısal boyutlar, daha büyük gökyüzü alanları için kullanışlıdır. (Örneğin, Orion Kuşağı'nın üç yıldızı yaklaşık 4,5°'lik bir açısal boyuta sahiptir.) Bununla birlikte gökadaların, bulutsuların veya gece gökyüzündeki diğer nesnelerinin açısal boyutlarını ölçmek için daha rafine birimlere ihtiyaç duyulmaktadır.
Dolayısıyla, dereceler aşağıdaki şekilde alt birimlere ayrılır:
- Bir tam dairede 360 derece (°)
- Bir derecede 60 yay-dakika (′)
- Bir yay-dakikada 60 yay-saniye (″)
Bunu bir perspektife oturtmak gerekirse, Dünya'dan bakıldığında dolunay yaklaşık 1⁄2° veya 30′ (veya 1800″) kadardır. Ay'ın gökyüzündeki hareketi açısal boyutta ölçülebilir: Yaklaşık olarak her saatte 15° veya saniyede 15″. Ay'ın yüzeyine çizilmiş bir mil uzunluğundaki çizgi, Dünya'dan bakıldığında yaklaşık 1″ uzunluğunda görünecektir.
Astronomide, bir gök cismine olan mesafeyi doğrudan ölçmek genellikle zordur, fakat nesnenin bilinen bir fiziksel boyutu (belki de mesafesi bilinen daha yakın bir nesneye benzeyen) ve ölçülebilir bir açısal çapı olabilir. Bu durumda, açısal çap formülü ters çevrilerek uzak cisimlere olan açısal çap mesafesi aşağıdaki gibi elde edilebilir:
Genişleyen evrenimiz gibi Öklidyen olmayan uzayda, açısal çap mesafesi çeşitli mesafe tanımlamalarından yalnızca biridir, bu nedenle aynı cisim için farklı "mesafeler" olabilir.
Dairesel olmayan nesneler[değiştir | kaynağı değiştir]
Gökadalar ve bulutsular gibi birçok derin gökyüzü nesnesi dairesel görünmez ve bu nedenle tipik olarak iki çap ölçüsü verilir: Büyük eksen ve küçük eksen. Örneğin, Küçük Macellan Bulutu 5° 20′ × 3° 5′ görsel görünür çapa sahiptir.
Aydınlatma eksikliği[değiştir | kaynağı değiştir]
Aydınlatma eksikliği, belirli bir gözlemci tarafından görülen bir gök cisminin aydınlatılmamış kısmının maksimum açısal genişliğidir. Örneğin, bir cisim 40″ yay genişliğindeyse ve %75 oranında aydınlatılmışsa, aydınlatma eksikliği 10″ olur.
Ayrıca bakınız[değiştir | kaynağı değiştir]
Kaynakça[değiştir | kaynağı değiştir]
- ^ Yanoff, Myron; Duker, Jay S. (2009). Ophthalmology 3rd Edition. MOSBY Elsevier. s. 54. ISBN 978-0444511416.
- ^ "Circular Segment". 21 Aralık 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Ocak 2015.
- ^ "A Taylor series for the functionarctan" (PDF). 18 Şubat 2015 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 23 Ocak 2015.
- ^ "Coordinate Systems". 21 Ocak 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 21 Ocak 2015.
- ^ "Photographing Satellites". 8 Haziran 2013. 21 Ocak 2015 tarihinde kaynağından arşivlendi.
- ^ Michael A. Seeds; Dana E. Backman (2010). Stars and Galaxies (7 bas.). Brooks Cole. s. 39. ISBN 978-0-538-73317-5.
- ^ O'Meara, Stephen James (6 Ağustos 2019). "The coalsacks of Cygnus". Astronomy.com. 10 Şubat 2023 tarihinde kaynağından arşivlendi. Erişim tarihi: 10 Şubat 2023.
- ^ Dobashi, Kazuhito; Matsumoto, Tomoaki; Shimoikura, Tomomi; Saito, Hiro; Akisato, Ko; Ohashi, Kenjiro; Nakagomi, Keisuke (24 Kasım 2014). "Colliding Filaments and a Massive Dense Core in the Cygnus Ob 7 Molecular Cloud". The Astrophysical Journal. American Astronomical Society. 797 (1): 58. arXiv:1411.0942 $2. Bibcode:2014ApJ...797...58D. doi:10.1088/0004-637x/797/1/58. ISSN 1538-4357.
- ^ Gorkavyi, Nick; Krotkov, Nickolay; Marshak, Alexander (24 Mart 2023). "Earth observations from the Moon's surface: dependence on lunar libration". Atmospheric Measurement Techniques. Copernicus GmbH. 16 (6): 1527-1537. Bibcode:2023AMT....16.1527G. doi:10.5194/amt-16-1527-2023. ISSN 1867-8548.
- ^ "Problem 346: The International Space Station and a Sunspot: Exploring angular scales" (PDF). Space Math @ NASA !. 19 Ağustos 2018. 10 Ağustos 2023 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 20 Mayıs 2022.
- ^ a b Wong, Yan (24 Ocak 2016). "How small can the naked eye see?". BBC Science Focus Magazine. 22 Mart 2023 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Mayıs 2022.
- ^ a b "Sharp eyes: how well can we really see?". Science in School – scienceinschool.org. 7 Eylül 2016. 17 Mayıs 2022 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Mayıs 2022.
- ^ Graney, Christopher M. (10 Aralık 2006). "The Accuracy of Galileo's Observations and the Early Search for Stellar Parallax". arXiv:physics/0612086 $2. doi:10.1007/3-540-50906-2_2.
- ^ "Galileo's telescope - How it works". Esposizioni on-line - Istituto e Museo di Storia della Scienza (İtalyanca). 23 Mart 2008 tarihinde kaynağından arşivlendi. Erişim tarihi: 21 Mayıs 2022.
- ^ Alnitak'ın Dünya'dan görülen açısal çapından 800.000 kat daha küçük. Alnitak mavi bir yıldız olduğu için boyutuna göre çok fazla ışık yayar. Eğer 800.000 kat daha uzakta olsaydı Hubble'ın görebileceği sınırda, 31,5 kadir büyüklüğünde olurdu.
Dış bağlantılar[değiştir | kaynağı değiştir]
- Small-Angle Formula (İngilizce) (7 Ekim 1997 tarihinde arşivlendi)
- Gezegenlerin Görünen Büyüklüklerine İlişkin Görsel Yardım (İngilizce)














