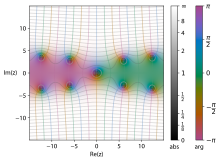
Hiperbolik sinüs integral fonksiyonu Shi(z)'nin karmaşık düzlemde
−
2
−
2
i
{\displaystyle -2-2i}
ile
2
+
2
i
{\displaystyle 2+2i}
arasında
Mathematica 13.1
ComplexPlot3D fonksiyonu ile oluşturulan renklerle çizimi
Si(x ) (mavi ) ve Ci(x ) (yeşil ) aynı grafik üzerinde gösterilmiştir.
Karmaşık düzlemde integral kosinüs. Negatif reel eksen boyunca
dal kesimine dikkat edin.
Matematikte , trigonometrik integraller trigonometrik fonksiyonları içeren temel olmayan integrallerin ailesidir .
0 ≤ x ≤ 8π için Si(x ) grafiği.
Karmaşık düzlemde kosinüs integral fonksiyonu Ci(
z )'nin
−
2
−
2
i
{\displaystyle -2-2i}
ile
2
+
2
i
{\displaystyle 2+2i}
arasında
Mathematica 13.1
ComplexPlot3D fonksiyonu ile oluşturulan renklerle çizimi
Farklı sinüs integral tanımları şunlardır:
Si
(
x
)
=
∫
0
x
sin
t
t
d
t
{\displaystyle \operatorname {Si} (x)=\int _{0}^{x}{\frac {\sin t}{t}}\,dt}
si
(
x
)
=
−
∫
x
∞
sin
t
t
d
t
.
{\displaystyle \operatorname {si} (x)=-\int _{x}^{\infty }{\frac {\sin t}{t}}\,dt~.}
sin
(
t
)
t
{\displaystyle {\frac {\sin(t)}{t}}}
sinc fonksiyonu ve aynı zamanda sıfırıncı küresel Bessel fonksiyonu olduğuna dikkat edin.
Çünkü sinc bir çift tam fonksiyon (holomorfik tüm karmaşık düzlem üzerinde), Si tamdır, tektir ve tanımındaki integral, uç noktaları birleştiren herhangi bir yol boyunca alınabilir.
Tanım olarak Si(x ) , sin x / x 'in x = 0ters türevidir ve si(x ) ise x = ∞Dirichlet integrali tarafından verilir,
Si
(
x
)
−
si
(
x
)
=
∫
0
∞
sin
t
t
d
t
=
π
2
veya
Si
(
x
)
=
π
2
+
si
(
x
)
.
{\displaystyle \operatorname {Si} (x)-\operatorname {si} (x)=\int _{0}^{\infty }{\frac {\sin t}{t}}\,dt={\frac {\pi }{2}}\quad {\text{ veya }}\quad \operatorname {Si} (x)={\frac {\pi }{2}}+\operatorname {si} (x)~.}
Sinyal işlemede , sinüs integralinin salınımları sinc filtresi kullanıldığında aşırı salınım ve halkasal bozulmaya ve alçak geçiren filtre olarak kesilmiş bir sinc filtresi kullanıldığında frekans etki alanı bozulmaya neden olur.
Bununla ilgili Gibbs fenomeni vardır: Sinüs integrali, sinc fonksiyonunun Heaviside basamak fonksiyonu ile konvolüsyonu olarak kabul edilirse, bu Gibbs fenomeninin nedeni olan Fourier serisinin kesilmesine karşılık gelir.
0 < x ≤ 8π için Ci(x ) grafiği.
Farklı kosinüs integral tanımları şunlardır:
Cin
(
x
)
=
∫
0
x
1
−
cos
t
t
d
t
,
{\displaystyle \operatorname {Cin} (x)=\int _{0}^{x}{\frac {1-\cos t}{t}}\,dt~,}
Ci
(
x
)
=
−
∫
x
∞
cos
t
t
d
t
=
γ
+
ln
x
−
∫
0
x
1
−
cos
t
t
d
t
|
Arg
(
x
)
|
<
π
için
,
{\displaystyle \operatorname {Ci} (x)=-\int _{x}^{\infty }{\frac {\cos t}{t}}\,dt=\gamma +\ln x-\int _{0}^{x}{\frac {1-\cos t}{t}}\,dt\qquad ~\left|\operatorname {Arg} (x)\right|<\pi ~{\text{ için }},}
burada γ ≈ 0,57721566 ...Euler-Mascheroni sabitidir . Bazı metinlerde Ci yerine ci kullanılır.
Ci(x ) , cos x / x (
x
→
∞
{\displaystyle x\to \infty }
Ci
(
x
)
=
γ
+
ln
x
−
Cin
(
x
)
\operatorname {Ci} (x)=\gamma +\ln x-\operatorname {Cin} (x)~
ile ilişkilidir. Cin bir çift , tam fonksiyondur . Bu nedenle, bazı metinler Cin 'i birincil fonksiyon olarak ele alır ve Ci 'yi Cin cinsinden türetir.
Hiperbolik sinüs integrali şu şekilde tanımlanır:
Shi
(
x
)
=
∫
0
x
sinh
(
t
)
t
d
t
.
{\displaystyle \operatorname {Shi} (x)=\int _{0}^{x}{\frac {\sinh(t)}{t}}\,dt.}
Sıradan sinüs integrali ile şu şekilde ilişkilidir:
Si
(
i
x
)
=
i
Shi
(
x
)
.
{\displaystyle \operatorname {Si} (ix)=i\operatorname {Shi} (x).}
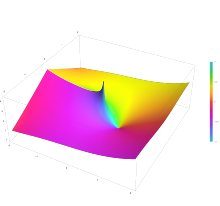
Hiperbolik kosinüs integral fonksiyonu Chi(z)'nin karmaşık düzlemde
−
2
−
2
i
{\displaystyle -2-2i}
ile
2
+
2
i
{\displaystyle 2+2i}
arasında
Mathematica 13.1
ComplexPlot3D fonksiyonu ile oluşturulan renklerle çizimi
Hiperbolik kosinüs integrali şöyledir:
Chi
(
x
)
=
γ
+
ln
x
+
∫
0
x
cosh
t
−
1
t
d
t
|
Arg
(
x
)
|
<
π
için
,
{\displaystyle \operatorname {Chi} (x)=\gamma +\ln x+\int _{0}^{x}{\frac {\cosh t-1}{t}}\,dt\qquad ~\left|\operatorname {Arg} (x)\right|<\pi ~{\text{ için }}~,}
burada
γ
{\displaystyle \gamma }
Euler-Mascheroni sabitidir .
Aşağıdaki seri açılımına sahiptir:
Chi
(
x
)
=
γ
+
ln
(
x
)
+
x
2
4
+
x
4
96
+
x
6
4320
+
x
8
322560
+
x
10
36288000
+
O
(
x
12
)
.
{\displaystyle \operatorname {Chi} (x)=\gamma +\ln(x)+{\frac {x^{2}}{4}}+{\frac {x^{4}}{96}}+{\frac {x^{6}}{4320}}+{\frac {x^{8}}{322560}}+{\frac {x^{10}}{36288000}}+O(x^{12}).}
Trigonometrik integraller, "yardımcı fonksiyonlar " olarak adlandırılan terimlerle anlaşılabilir.
f
(
x
)
≡
∫
0
∞
sin
(
t
)
t
+
x
d
t
=
∫
0
∞
e
−
x
t
t
2
+
1
d
t
=
Ci
(
x
)
sin
(
x
)
+
[
π
2
−
Si
(
x
)
]
cos
(
x
)
,
g
(
x
)
≡
∫
0
∞
cos
(
t
)
t
+
x
d
t
=
∫
0
∞
t
e
−
x
t
t
2
+
1
d
t
=
−
Ci
(
x
)
cos
(
x
)
+
[
π
2
−
Si
(
x
)
]
sin
(
x
)
.
{\displaystyle {\begin{array}{rcl}f(x)&\equiv &\int _{0}^{\infty }{\frac {\sin(t)}{t+x}}\,dt&=&\int _{0}^{\infty }{\frac {e^{-xt}}{t^{2}+1}}\,dt&=&\operatorname {Ci} (x)\sin(x)+\left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\cos(x)~,\\g(x)&\equiv &\int _{0}^{\infty }{\frac {\cos(t)}{t+x}}\,dt&=&\int _{0}^{\infty }{\frac {te^{-xt}}{t^{2}+1}}\,dt&=&-\operatorname {Ci} (x)\cos(x)+\left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\sin(x)~.\end{array}}}
Bu fonksiyonlar kullanılarak trigonometrik integraller aşağıdaki gibi yeniden ifade edilebilir
(bkz. Abramowitz & Stegun, s. 232 )
π
2
−
Si
(
x
)
=
−
si
(
x
)
=
f
(
x
)
cos
(
x
)
+
g
(
x
)
sin
(
x
)
,
ve
Ci
(
x
)
=
f
(
x
)
sin
(
x
)
−
g
(
x
)
cos
(
x
)
.
{\displaystyle {\begin{array}{rcl}{\frac {\pi }{2}}-\operatorname {Si} (x)=-\operatorname {si} (x)&=&f(x)\cos(x)+g(x)\sin(x)~,\qquad {\text{ ve }}\\\operatorname {Ci} (x)&=&f(x)\sin(x)-g(x)\cos(x)~.\\\end{array}}}
si , ci parametrik grafiği ile oluşturulan spiral , Nielsen spirali olarak bilinir.
x
(
t
)
=
a
×
ci
(
t
)
{\displaystyle x(t)=a\times \operatorname {ci} (t)}
y
(
t
)
=
a
×
si
(
t
)
{\displaystyle y(t)=a\times \operatorname {si} (t)}
Sarmal, Fresnel integrali ve Euler spirali ile yakından ilişkilidir. Nielsen spiralinin görüntü işleme, yol ve iz yapımı ve diğer alanlarda uygulamaları vardır.[ 1]
Trigonometrik integrallerin değerlendirilmesi için argümanın aralığına bağlı olarak çeşitli açılımlar kullanılabilir.
Si
(
x
)
∼
π
2
−
cos
x
x
(
1
−
2
!
x
2
+
4
!
x
4
−
6
!
x
6
⋯
)
−
sin
x
x
(
1
x
−
3
!
x
3
+
5
!
x
5
−
7
!
x
7
⋯
)
{\displaystyle \operatorname {Si} (x)\sim {\frac {\pi }{2}}-{\frac {\cos x}{x}}\left(1-{\frac {2!}{x^{2}}}+{\frac {4!}{x^{4}}}-{\frac {6!}{x^{6}}}\cdots \right)-{\frac {\sin x}{x}}\left({\frac {1}{x}}-{\frac {3!}{x^{3}}}+{\frac {5!}{x^{5}}}-{\frac {7!}{x^{7}}}\cdots \right)}
Ci
(
x
)
∼
sin
x
x
(
1
−
2
!
x
2
+
4
!
x
4
−
6
!
x
6
⋯
)
−
cos
x
x
(
1
x
−
3
!
x
3
+
5
!
x
5
−
7
!
x
7
⋯
)
.
{\displaystyle \operatorname {Ci} (x)\sim {\frac {\sin x}{x}}\left(1-{\frac {2!}{x^{2}}}+{\frac {4!}{x^{4}}}-{\frac {6!}{x^{6}}}\cdots \right)-{\frac {\cos x}{x}}\left({\frac {1}{x}}-{\frac {3!}{x^{3}}}+{\frac {5!}{x^{5}}}-{\frac {7!}{x^{7}}}\cdots \right)~.}
Bu seriler asimptotik ve ıraksaktır, ancak ℜ(x ) ≫ 1 değerinde tahminler ve hatta kesin değerlendirme için kullanılabilir.
Si
(
x
)
=
∑
n
=
0
∞
(
−
1
)
n
x
2
n
+
1
(
2
n
+
1
)
(
2
n
+
1
)
!
=
x
−
x
3
3
!
⋅
3
+
x
5
5
!
⋅
5
−
x
7
7
!
⋅
7
±
⋯
{\displaystyle \operatorname {Si} (x)=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)(2n+1)!}}=x-{\frac {x^{3}}{3!\cdot 3}}+{\frac {x^{5}}{5!\cdot 5}}-{\frac {x^{7}}{7!\cdot 7}}\pm \cdots }
Ci
(
x
)
=
γ
+
ln
x
+
∑
n
=
1
∞
(
−
1
)
n
x
2
n
2
n
(
2
n
)
!
=
γ
+
ln
x
−
x
2
2
!
⋅
2
+
x
4
4
!
⋅
4
∓
⋯
{\displaystyle \operatorname {Ci} (x)=\gamma +\ln x+\sum _{n=1}^{\infty }{\frac {(-1)^{n}x^{2n}}{2n(2n)!}}=\gamma +\ln x-{\frac {x^{2}}{2!\cdot 2}}+{\frac {x^{4}}{4!\cdot 4}}\mp \cdots }
Bu seriler herhangi bir kompleks x değerinde yakınsaktır, ancak |x için seri başlangıçta yavaş yakınsayacak ve yüksek hassasiyet için birçok terim gerektirecektir.
Sinüsün Maclaurin serisi açılımından:
sin
x
=
x
−
x
3
3
!
+
x
5
5
!
−
x
7
7
!
+
x
9
9
!
−
x
11
11
!
+
⋯
\sin \,x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+{\frac {x^{9}}{9!}}-{\frac {x^{11}}{11!}}+\cdots
sin
x
x
=
1
−
x
2
3
!
+
x
4
5
!
−
x
6
7
!
+
x
8
9
!
−
x
10
11
!
+
⋯
{\displaystyle {\frac {\sin \,x}{x}}=1-{\frac {x^{2}}{3!}}+{\frac {x^{4}}{5!}}-{\frac {x^{6}}{7!}}+{\frac {x^{8}}{9!}}-{\frac {x^{10}}{11!}}+\cdots }
∴
∫
sin
x
x
d
x
=
x
−
x
3
3
!
⋅
3
+
x
5
5
!
⋅
5
−
x
7
7
!
⋅
7
+
x
9
9
!
⋅
9
−
x
11
11
!
⋅
11
+
⋯
{\displaystyle \therefore \int {\frac {\sin \,x}{x}}dx=x-{\frac {x^{3}}{3!\cdot 3}}+{\frac {x^{5}}{5!\cdot 5}}-{\frac {x^{7}}{7!\cdot 7}}+{\frac {x^{9}}{9!\cdot 9}}-{\frac {x^{11}}{11!\cdot 11}}+\cdots }
E
1
(
z
)
=
∫
1
∞
exp
(
−
z
t
)
t
d
t
for
ℜ
(
z
)
≥
0
{\displaystyle \operatorname {E} _{1}(z)=\int _{1}^{\infty }{\frac {\exp(-zt)}{t}}\,dt\qquad ~{\text{ for }}~\Re (z)\geq 0}
fonksiyonu üstel integral olarak adlandırılır. Bu integral, Si ve Ci ile yakından ilişkilidir;
E
1
(
i
x
)
=
i
(
−
π
2
+
Si
(
x
)
)
−
Ci
(
x
)
=
i
si
(
x
)
−
ci
(
x
)
for
x
>
0
.
{\displaystyle \operatorname {E} _{1}(ix)=i\left(-{\frac {\pi }{2}}+\operatorname {Si} (x)\right)-\operatorname {Ci} (x)=i\operatorname {si} (x)-\operatorname {ci} (x)\qquad ~{\text{ for }}~x>0~.}
İlgili her bir fonksiyon, argümanın negatif değerlerindeki kesim dışında analitik olduğundan, bağıntının geçerlilik alanı genişletilmelidir (Bu aralığın dışında, π
Genelleştirilmiş integro-üstel fonksiyonun sanal argümanının durumları şunlardır:
∫
1
∞
cos
(
a
x
)
ln
x
x
d
x
=
−
π
2
24
+
γ
(
γ
2
+
ln
a
)
+
ln
2
a
2
+
∑
n
≥
1
(
−
a
2
)
n
(
2
n
)
!
(
2
n
)
2
,
{\displaystyle \int _{1}^{\infty }\cos(ax){\frac {\ln x}{x}}\,dx=-{\frac {\pi ^{2}}{24}}+\gamma \left({\frac {\gamma }{2}}+\ln a\right)+{\frac {\ln ^{2}a}{2}}+\sum _{n\geq 1}{\frac {(-a^{2})^{n}}{(2n)!(2n)^{2}}}~,}
∫
1
∞
e
i
a
x
ln
x
x
d
x
=
−
π
2
24
+
γ
(
γ
2
+
ln
a
)
+
ln
2
a
2
−
π
2
i
(
γ
+
ln
a
)
+
∑
n
≥
1
(
i
a
)
n
n
!
n
2
.
{\displaystyle \int _{1}^{\infty }e^{iax}{\frac {\ln x}{x}}\,dx=-{\frac {\pi ^{2}}{24}}+\gamma \left({\frac {\gamma }{2}}+\ln a\right)+{\frac {\ln ^{2}a}{2}}-{\frac {\pi }{2}}i\left(\gamma +\ln a\right)+\sum _{n\geq 1}{\frac {(ia)^{n}}{n!n^{2}}}~.}
∫
1
∞
e
i
a
x
ln
x
x
2
d
x
=
1
+
i
a
[
−
π
2
24
+
γ
(
γ
2
+
ln
a
−
1
)
+
ln
2
a
2
−
ln
a
+
1
]
+
π
a
2
(
γ
+
ln
a
−
1
)
+
∑
n
≥
1
(
i
a
)
n
+
1
(
n
+
1
)
!
n
2
.
{\displaystyle \int _{1}^{\infty }e^{iax}{\frac {\ln x}{x^{2}}}\,dx=1+ia\left[-{\frac {\pi ^{2}}{24}}+\gamma \left({\frac {\gamma }{2}}+\ln a-1\right)+{\frac {\ln ^{2}a}{2}}-\ln a+1\right]+{\frac {\pi a}{2}}{\Bigl (}\gamma +\ln a-1{\Bigr )}+\sum _{n\geq 1}{\frac {(ia)^{n+1}}{(n+1)!n^{2}}}~.}
Yakınsak Taylor serilerinin Padé yaklaşımları , küçük argümanlar için fonksiyonları değerlendirmenin etkili bir yolunu sağlar. Rowe ve diğerleri (2015)[ 2] 0 ≤ x ≤ 4 için 10-16 'dan daha doğrudur,
Si
(
x
)
≈
x
⋅
(
1
−
4.54393409816329991
⋅
10
−
2
⋅
x
2
+
1.15457225751016682
⋅
10
−
3
⋅
x
4
−
1.41018536821330254
⋅
10
−
5
⋅
x
6
+
9.43280809438713025
⋅
10
−
8
⋅
x
8
−
3.53201978997168357
⋅
10
−
10
⋅
x
10
+
7.08240282274875911
⋅
10
−
13
⋅
x
12
−
6.05338212010422477
⋅
10
−
16
⋅
x
14
1
+
1.01162145739225565
⋅
10
−
2
⋅
x
2
+
4.99175116169755106
⋅
10
−
5
⋅
x
4
+
1.55654986308745614
⋅
10
−
7
⋅
x
6
+
3.28067571055789734
⋅
10
−
10
⋅
x
8
+
4.5049097575386581
⋅
10
−
13
⋅
x
10
+
3.21107051193712168
⋅
10
−
16
⋅
x
12
)
Ci
(
x
)
≈
γ
+
ln
(
x
)
+
x
2
⋅
(
−
0.25
+
7.51851524438898291
⋅
10
−
3
⋅
x
2
−
1.27528342240267686
⋅
10
−
4
⋅
x
4
+
1.05297363846239184
⋅
10
−
6
⋅
x
6
−
4.68889508144848019
⋅
10
−
9
⋅
x
8
+
1.06480802891189243
⋅
10
−
11
⋅
x
10
−
9.93728488857585407
⋅
10
−
15
⋅
x
12
1
+
1.1592605689110735
⋅
10
−
2
⋅
x
2
+
6.72126800814254432
⋅
10
−
5
⋅
x
4
+
2.55533277086129636
⋅
10
−
7
⋅
x
6
+
6.97071295760958946
⋅
10
−
10
⋅
x
8
+
1.38536352772778619
⋅
10
−
12
⋅
x
10
+
1.89106054713059759
⋅
10
−
15
⋅
x
12
+
1.39759616731376855
⋅
10
−
18
⋅
x
14
)
{\displaystyle {\begin{array}{rcl}\operatorname {Si} (x)&\approx &x\cdot \left({\frac {\begin{array}{l}1-4.54393409816329991\cdot 10^{-2}\cdot x^{2}+1.15457225751016682\cdot 10^{-3}\cdot x^{4}-1.41018536821330254\cdot 10^{-5}\cdot x^{6}\\~~~+9.43280809438713025\cdot 10^{-8}\cdot x^{8}-3.53201978997168357\cdot 10^{-10}\cdot x^{10}+7.08240282274875911\cdot 10^{-13}\cdot x^{12}\\~~~-6.05338212010422477\cdot 10^{-16}\cdot x^{14}\end{array}}{\begin{array}{l}1+1.01162145739225565\cdot 10^{-2}\cdot x^{2}+4.99175116169755106\cdot 10^{-5}\cdot x^{4}+1.55654986308745614\cdot 10^{-7}\cdot x^{6}\\~~~+3.28067571055789734\cdot 10^{-10}\cdot x^{8}+4.5049097575386581\cdot 10^{-13}\cdot x^{10}+3.21107051193712168\cdot 10^{-16}\cdot x^{12}\end{array}}}\right)\\&~&\\\operatorname {Ci} (x)&\approx &\gamma +\ln(x)+\\&&x^{2}\cdot \left({\frac {\begin{array}{l}-0.25+7.51851524438898291\cdot 10^{-3}\cdot x^{2}-1.27528342240267686\cdot 10^{-4}\cdot x^{4}+1.05297363846239184\cdot 10^{-6}\cdot x^{6}\\~~~-4.68889508144848019\cdot 10^{-9}\cdot x^{8}+1.06480802891189243\cdot 10^{-11}\cdot x^{10}-9.93728488857585407\cdot 10^{-15}\cdot x^{12}\\\end{array}}{\begin{array}{l}1+1.1592605689110735\cdot 10^{-2}\cdot x^{2}+6.72126800814254432\cdot 10^{-5}\cdot x^{4}+2.55533277086129636\cdot 10^{-7}\cdot x^{6}\\~~~+6.97071295760958946\cdot 10^{-10}\cdot x^{8}+1.38536352772778619\cdot 10^{-12}\cdot x^{10}+1.89106054713059759\cdot 10^{-15}\cdot x^{12}\\~~~+1.39759616731376855\cdot 10^{-18}\cdot x^{14}\\\end{array}}}\right)\end{array}}}
İntegraller, yardımcı fonksiyonlar aracılığıyla dolaylı olarak değerlendirilebilir.
f
(
x
)
{\displaystyle f(x)}
g
(
x
)
{\displaystyle g(x)}
Si
(
x
)
=
π
2
−
f
(
x
)
cos
(
x
)
−
g
(
x
)
sin
(
x
)
{\displaystyle \operatorname {Si} (x)={\frac {\pi }{2}}-f(x)\cos(x)-g(x)\sin(x)}
Ci
(
x
)
=
f
(
x
)
sin
(
x
)
−
g
(
x
)
cos
(
x
)
{\displaystyle \operatorname {Ci} (x)=f(x)\sin(x)-g(x)\cos(x)}
veya eşdeğer olarak
f
(
x
)
≡
[
π
2
−
Si
(
x
)
]
cos
(
x
)
+
Ci
(
x
)
sin
(
x
)
{\displaystyle f(x)\equiv \left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\cos(x)+\operatorname {Ci} (x)\sin(x)}
g
(
x
)
≡
[
π
2
−
Si
(
x
)
]
sin
(
x
)
−
Ci
(
x
)
cos
(
x
)
{\displaystyle g(x)\equiv \left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\sin(x)-\operatorname {Ci} (x)\cos(x)}
x
≥
4
{\displaystyle x\geq 4}
Padé rasyonel fonksiyonları
f
(
x
)
{\displaystyle f(x)}
g
(
x
)
{\displaystyle g(x)}
−16 'dan daha az hata ile yaklaşır:[ 2]
f
(
x
)
≈
1
x
⋅
(
1
+
7.44437068161936700618
⋅
10
2
⋅
x
−
2
+
1.96396372895146869801
⋅
10
5
⋅
x
−
4
+
2.37750310125431834034
⋅
10
7
⋅
x
−
6
+
1.43073403821274636888
⋅
10
9
⋅
x
−
8
+
4.33736238870432522765
⋅
10
10
⋅
x
−
10
+
6.40533830574022022911
⋅
10
11
⋅
x
−
12
+
4.20968180571076940208
⋅
10
12
⋅
x
−
14
+
1.00795182980368574617
⋅
10
13
⋅
x
−
16
+
4.94816688199951963482
⋅
10
12
⋅
x
−
18
−
4.94701168645415959931
⋅
10
11
⋅
x
−
20
1
+
7.46437068161927678031
⋅
10
2
⋅
x
−
2
+
1.97865247031583951450
⋅
10
5
⋅
x
−
4
+
2.41535670165126845144
⋅
10
7
⋅
x
−
6
+
1.47478952192985464958
⋅
10
9
⋅
x
−
8
+
4.58595115847765779830
⋅
10
10
⋅
x
−
10
+
7.08501308149515401563
⋅
10
11
⋅
x
−
12
+
5.06084464593475076774
⋅
10
12
⋅
x
−
14
+
1.43468549171581016479
⋅
10
13
⋅
x
−
16
+
1.11535493509914254097
⋅
10
13
⋅
x
−
18
)
g
(
x
)
≈
1
x
2
⋅
(
1
+
8.1359520115168615
⋅
10
2
⋅
x
−
2
+
2.35239181626478200
⋅
10
5
⋅
x
−
4
+
3.12557570795778731
⋅
10
7
⋅
x
−
6
+
2.06297595146763354
⋅
10
9
⋅
x
−
8
+
6.83052205423625007
⋅
10
10
⋅
x
−
10
+
1.09049528450362786
⋅
10
12
⋅
x
−
12
+
7.57664583257834349
⋅
10
12
⋅
x
−
14
+
1.81004487464664575
⋅
10
13
⋅
x
−
16
+
6.43291613143049485
⋅
10
12
⋅
x
−
18
−
1.36517137670871689
⋅
10
12
⋅
x
−
20
1
+
8.19595201151451564
⋅
10
2
⋅
x
−
2
+
2.40036752835578777
⋅
10
5
⋅
x
−
4
+
3.26026661647090822
⋅
10
7
⋅
x
−
6
+
2.23355543278099360
⋅
10
9
⋅
x
−
8
+
7.87465017341829930
⋅
10
10
⋅
x
−
10
+
1.39866710696414565
⋅
10
12
⋅
x
−
12
+
1.17164723371736605
⋅
10
13
⋅
x
−
14
+
4.01839087307656620
⋅
10
13
⋅
x
−
16
+
3.99653257887490811
⋅
10
13
⋅
x
−
18
)
{\displaystyle {\begin{array}{rcl}f(x)&\approx &{\dfrac {1}{x}}\cdot \left({\frac {\begin{array}{l}1+7.44437068161936700618\cdot 10^{2}\cdot x^{-2}+1.96396372895146869801\cdot 10^{5}\cdot x^{-4}+2.37750310125431834034\cdot 10^{7}\cdot x^{-6}\\~~~+1.43073403821274636888\cdot 10^{9}\cdot x^{-8}+4.33736238870432522765\cdot 10^{10}\cdot x^{-10}+6.40533830574022022911\cdot 10^{11}\cdot x^{-12}\\~~~+4.20968180571076940208\cdot 10^{12}\cdot x^{-14}+1.00795182980368574617\cdot 10^{13}\cdot x^{-16}+4.94816688199951963482\cdot 10^{12}\cdot x^{-18}\\~~~-4.94701168645415959931\cdot 10^{11}\cdot x^{-20}\end{array}}{\begin{array}{l}1+7.46437068161927678031\cdot 10^{2}\cdot x^{-2}+1.97865247031583951450\cdot 10^{5}\cdot x^{-4}+2.41535670165126845144\cdot 10^{7}\cdot x^{-6}\\~~~+1.47478952192985464958\cdot 10^{9}\cdot x^{-8}+4.58595115847765779830\cdot 10^{10}\cdot x^{-10}+7.08501308149515401563\cdot 10^{11}\cdot x^{-12}\\~~~+5.06084464593475076774\cdot 10^{12}\cdot x^{-14}+1.43468549171581016479\cdot 10^{13}\cdot x^{-16}+1.11535493509914254097\cdot 10^{13}\cdot x^{-18}\end{array}}}\right)\\&&\\g(x)&\approx &{\dfrac {1}{x^{2}}}\cdot \left({\frac {\begin{array}{l}1+8.1359520115168615\cdot 10^{2}\cdot x^{-2}+2.35239181626478200\cdot 10^{5}\cdot x^{-4}+3.12557570795778731\cdot 10^{7}\cdot x^{-6}\\~~~+2.06297595146763354\cdot 10^{9}\cdot x^{-8}+6.83052205423625007\cdot 10^{10}\cdot x^{-10}+1.09049528450362786\cdot 10^{12}\cdot x^{-12}\\~~~+7.57664583257834349\cdot 10^{12}\cdot x^{-14}+1.81004487464664575\cdot 10^{13}\cdot x^{-16}+6.43291613143049485\cdot 10^{12}\cdot x^{-18}\\~~~-1.36517137670871689\cdot 10^{12}\cdot x^{-20}\end{array}}{\begin{array}{l}1+8.19595201151451564\cdot 10^{2}\cdot x^{-2}+2.40036752835578777\cdot 10^{5}\cdot x^{-4}+3.26026661647090822\cdot 10^{7}\cdot x^{-6}\\~~~+2.23355543278099360\cdot 10^{9}\cdot x^{-8}+7.87465017341829930\cdot 10^{10}\cdot x^{-10}+1.39866710696414565\cdot 10^{12}\cdot x^{-12}\\~~~+1.17164723371736605\cdot 10^{13}\cdot x^{-14}+4.01839087307656620\cdot 10^{13}\cdot x^{-16}+3.99653257887490811\cdot 10^{13}\cdot x^{-18}\end{array}}}\right)\\\end{array}}}
Mathar, R.J. (2009). "Numerical evaluation of the oscillatory integral over exp(iπ x )·x 1/x between 1 and ∞". Appendix B. arXiv :0912.3844 $2 Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. (2007). "Section 6.8.2 – Cosine and Sine Integrals" . Numerical Recipes: The Art of Scientific Computing . 3rd. New York: Cambridge University Press. ISBN 978-0-521-88068-8 . Sloughter, Dan. "Sine Integral Taylor series proof" (PDF) . Difference Equations to Differential Equations . Temme, N.M. (2010), "Exponential, Logarithmic, Sine, and Cosine Integrals" , Olver, Frank W. J. ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (Ed.), NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 , MR 2723248 Eric W. Weisstein , Sine Integral MathWorld )Hazewinkel, Michiel, (Ed.) (2001), "Integral sine" , Encyclopaedia of Mathematics ISBN 978-1556080104 Hazewinkel, Michiel, (Ed.) (2001), "Integral cosine" , Encyclopaedia of Mathematics ISBN 978-1556080104 
_in_the_complex_plane_from_-2-2i_to_2%2B2i_with_colors_created_with_Mathematica_13.1_function_ComplexPlot3D.svg)
_in_the_complex_plane_from_-2-2i_to_2%2B2i_with_colors_created_with_Mathematica_13.1_function_ComplexPlot3D.svg)
_in_the_complex_plane_from_-2-2i_to_2%2B2i_with_colors_created_with_Mathematica_13.1_function_ComplexPlot3D.svg)
![{\displaystyle {\begin{array}{rcl}f(x)&\equiv &\int _{0}^{\infty }{\frac {\sin(t)}{t+x}}\,dt&=&\int _{0}^{\infty }{\frac {e^{-xt}}{t^{2}+1}}\,dt&=&\operatorname {Ci} (x)\sin(x)+\left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\cos(x)~,\\g(x)&\equiv &\int _{0}^{\infty }{\frac {\cos(t)}{t+x}}\,dt&=&\int _{0}^{\infty }{\frac {te^{-xt}}{t^{2}+1}}\,dt&=&-\operatorname {Ci} (x)\cos(x)+\left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\sin(x)~.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2b43b57fdff2c9f86d9685bbf1d8a0eb7b30c11)
![{\displaystyle \int _{1}^{\infty }e^{iax}{\frac {\ln x}{x^{2}}}\,dx=1+ia\left[-{\frac {\pi ^{2}}{24}}+\gamma \left({\frac {\gamma }{2}}+\ln a-1\right)+{\frac {\ln ^{2}a}{2}}-\ln a+1\right]+{\frac {\pi a}{2}}{\Bigl (}\gamma +\ln a-1{\Bigr )}+\sum _{n\geq 1}{\frac {(ia)^{n+1}}{(n+1)!n^{2}}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61671b32bbb8068361dfa5d582a6d6f3230a43cf)
![{\displaystyle f(x)\equiv \left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\cos(x)+\operatorname {Ci} (x)\sin(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a843910ab6cb92c362e68ac401c28c1e7cda148)
![{\displaystyle g(x)\equiv \left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\sin(x)-\operatorname {Ci} (x)\cos(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f74128afc0519376e13432f0e9f5b0bf6627de7)
