Moleküler dinamik


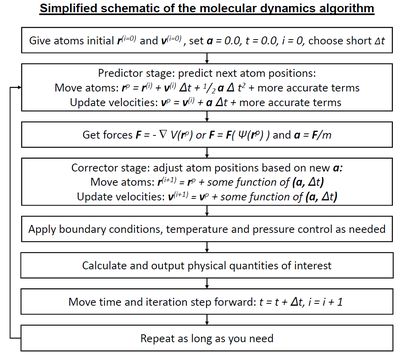
Moleküler dinamik (MD), atomların ve moleküllerin fiziksel hareketlerini incelemek için bir bilgisayar simülasyon yöntemidir. Atomların ve moleküllerin sabit bir süre boyunca etkileşime girmesine izin verilir ve bu da sistemin dinamik evrimi hakkında bilgi verir. En yaygın versiyonda, atomların ve moleküllerin yörüngeleri, parçacıklar ve bunların potansiyel enerjileri arasındaki kuvvetlerin çoğu zaman atomlararası potansiyeller veya moleküler mekanik kuvvet alanları kullanılarak hesaplandığı, etkileşen parçacıkların bir sistemi için Newton'un hareket denklemlerinin sayısal olarak çözülmesiyle belirlenir. Metot ilk olarak 1950'lerin sonunda teorik fizik alanında geliştirildi,[1] ancak günümüzde çoğunlukla kimyasal fizik, malzeme bilimi ve biyomoleküllerin modellenmesinde uygulanmaktadır .
Moleküler sistemler tipik olarak çok sayıda parçacıktan oluştuğundan, bu tür karmaşık sistemlerin özelliklerini analitik olarak belirlemek mümkün değildir; MD simülasyonu, sayısal yöntemleri kullanarak bu sorunu çözmektedir. Bununla birlikte, uzun MD simülasyonları matematiksel olarak kötü koşullandırılmıştırlar (yüksek koşul sayısına sahiptir), yani sayısal entegrasyonda uygun algoritma ve parametrelerin seçimi ile minimize edilebilecek, ancak tamamen ortadan kalkamayan kümülatif hatalar oluştururlar.
Ergodik hipoteze uyan sistemler için, bir moleküler dinamik simülasyonunun evrimi, sistemin makroskopik termodinamik özelliklerini belirlemek için kullanılabilir: bir ergodik sistemin zaman ortalamaları, mikrokanonik topluluk ortalamalarına karşılık gelir. MD, aynı zamanda doğanın kuvvetlerini[2] canlandırarak ve atomik bir ölçekte moleküler hareketi inceleme şansı sağlayarak "sayılarla istatistiksel mekanik" ve " Laplace'in Newton mekaniğinin vizyonu" olarak da adlandırılmıştır.
Tarih[değiştir | kaynağı değiştir]
Monte Carlo simülasyonlarının önceki başarılarından sonra, yöntem ilk kez 1950'lerin ortalarında Fermi, Pasta, Ulam ve Tsingou[1] tarafından geliştirilmiştir. 1957'de Alder ve Wainwright, sert küreler arasında mükemmel elastik çarpışmaları simüle etmek için bir IBM 704 bilgisayarı kullandı. 1960 yılında Gibson ve ark. yapışkan bir yüzey kuvveti ile birlikte Born-Mayer tipi itici etkileşimi kullanarak katı bakırın radyasyon hasarını simüle etti. 1964 yılında, Rahman, bir Lennard-Jones potansiyeli kullanan, sıvı argonun dönüm noktası simülasyonlarını yayınladı. Kendi kendine yayılma katsayısı gibi sistem özelliklerinin hesaplanması deneysel verilerle deneysel verilerle iyi karşılaştırıldı.
Moleküler dinamikleri bilgisayarlarla simüle etmek mümkün olmadan önce bazı insanlar atom hareketinin fiziksel modeller (örneğin makroskopik küreler) oluşturarak modellenmesi için yoğun bir çalışma üstlendi. Amaç, bu küreleri bir sıvının yapısını taklit edecek şekilde düzenlemek ve davranışını incelemek için kullanmaktı. JD Bernal, 1962’de şunları söyledi: “ ... Çok sayıda lastik top aldım ve bunları 2.75 ila 4 inç arasında değişen farklı uzunluklardaki çubuklarla bir araya getirdim. Bunu ilk etapta mümkün olduğunca rastgele yapmayı denedim, kendi ofisimde çalışıyor, her beş dakikada bir rahatsız ediliyor ve rahatsız edilmeden önce ne yaptığımı hatırlamıyordum. ”
Uygulama alanları[değiştir | kaynağı değiştir]
İlk olarak teorik fizikte kullanılan MD yöntemi, malzeme biliminde kısa süre sonra popülerlik kazanmıştır ve 1970'lerden beri biyokimya ve biyofizikte de yaygındır. MD, X ışını kristalografisi veya NMR spektroskopisinden elde edilen deneysel kısıtlamalara dayanarak proteinlerin ve diğer makromoleküllerin 3 boyutlu yapılarını geliştirmek/daha iyi hale getirmek için sıklıkla kullanılır. Fizikte, MD, ince film büyümesi ve iyon alt ekimi gibi doğrudan gözlemlenemeyen atomik seviye fenomenlerin dinamiklerini incelemek ve ayrıca henüz yaratılmayan veya henüz yaratılamayan nanoteknolojik cihazların fiziksel özelliklerini incelemek için kullanılır. Biyofizik ve yapısal biyolojide, bu yöntem proteinler ve nükleik asitler gibi makromoleküllerin hareketlerini incelemek için sıkça uygulanır. Burdan elde edilecek veri ligand yerleştirme gibi biyofiziksel deneylerin sonuçlarını yorumlamak ve diğer moleküller ile etkileşimleri modellemek için faydalı olabilir. Prensipte MD, polipeptit zincirinin rastgele katlanmasını simüle ederek protein yapısının ab initio tahmini için kullanılabilir.
Uygulama örnekleri[değiştir | kaynağı değiştir]

Moleküler dinamikler birçok bilim dalında kullanılmaktadır.
- Basitleştirilmiş bir biyolojik katlama işleminin ilk MD simülasyonu 1975'te yayınlandı. Nature'da yayınlanan simülasyon, modern bilgisayarlı protein katlamanın alanının yolunu açtı.
- Bir biyolojik sürecin ilk MD simülasyonu 1976'da yayınlandı. Nature'da yayınlanan simülasyonu, protein hareketini sadece yardımcı bir faktör olarak değil de bir temel işlev olarak gerekli görmenin yolunu açtı.
- MD, enerjik nötron ve iyon ışınlanmasının katı ve katı yüzeyler üzerindeki etkileri gibi ısı sivri uç rejimindeki (heat spike regime) çarpışma basamaklarını (çarpışma şelalerini) ele almak için standart bir yöntemdir.
- Gaucher Hastalığına neden olan en yaygın protein mutasyonu N370S'in moleküler temelini tahmin etmek için MD simülasyonları başarıyla uygulandı. Bunu takip eden daha sonraki bağımsız olarak yayınlanan yayında ise, bu kör tahminlerin aynı mutant üzerindeki deneysel çalışma ile yüksek bir korelasyon gösterdiği gösterilmiştir.
- Yüzey yüklerinin ince su filmlerinin metal yüzeyler üzerindeki ayrışma basıncı üzerindeki etkisini araştırmak için MD simülasyonları kullanılmıştır.
- MD simülasyonları transmisyon elektron mikroskobu görüntüsünün özelliklerini anlamak için çok kesitli görüntü simülasyonları ile birlikte kullanılır
- Hamiltonian-ikilemi algoritmaları ile birleştirilmiş MD hesaplamaları, DNA çift iplikçiklerinin hidrofobik[3] ve hidrofilik[4] tek duvarlı karbon nanotüpler üzerine kapsülleme termodinamiklerini araştırmak için kullanılmıştır.
Aşağıdaki biyofiziksel örnekler, çok büyük boyutta bir sistem (bir virüsün tamamı) veya çok uzun simülasyon sürelerde (1.112 milisaniyeye varan süreler) simülasyonları üretmek için kayda değer çabaları göstermektedir:
- Uydu tütün mozaik virüsünün tamamının MD simülasyonu (STMV) (2006, Boyut: 1 milyon atom, Simülasyon süresi: 50 ns, program: NAMD ): Bu virüs, Tütün Mozaik Virüsü (TMV) enfeksiyonunun belirtilerini kötüleştiren küçük, ikosahedral bitki virüsüdür. Viral düzeneğin mekanizmalarını araştırmak için moleküler dinamik simülasyonlar kullanılmıştır. STMV partikülünün tamamı, viral kapsidi (kaplama) oluşturan bir proteinin 60 özdeş kopyasından ve bir 1063 nükleotidli tek zincirli RNA genomundan oluşur . Bir anahtar bulgu, kapsidin içinde RNA olmadığında çok dengesiz olmasıdır. Simülasyonun tamamlanması 2006 model bir masaüstü bilgisayarda yaklaşık 35 yıl alacaktır. Bundan dolayı, görev birçok paralel işlemci ile aralarında sürekli iletişim oluşturarak yapıldı.
- Villin Başlığının tüm atom detaylarında katlanması simülasyonları (2006, Boyut: 20.000 atom; Simülasyon süresi: 500 =s = 500.000 ns, Program: Folding@home ) Bu simülasyon, dünya genelinde 200.000 CPU'nun katıldığı kişisel bilgisayarlarda yürütülmüştür. Bu bilgisayarlarda, Viford Pande tarafından Stanford Üniversitesi'nde koordine edilen geniş çaplı bir dağıtılmış hesaplama çalışması olan Folding @ home programı kuruldu. Villin Başlık proteininin kinetik özellikleri sürekli gerçek zamanlı iletişimden yoksun CPU'lar tarafından birçok bağımsız kısa yörünge (trajectories) kulanılarak araştırılmıştır. Kullanılan bir yöntem de, belirli bir başlangıç konformasyonunun açılmasından önce katlanma olasılığını ölçen Pfold değer analiziydi. Pfold geçiş durumu yapıları ve katlama yolağı boyuncaki konformasyon sırası hakkında bilgi verir. Pfold hesaplamasındaki her bir yörünge nispeten kısa olabilir, ancak birçok bağımsız yörüngeye ihtiyaç duyulur.
- Bu moleküler simülasyonlar, malzeme çıkarma mekanizmalarını, araç geometrisinin etkilerini, sıcaklık ve kesme hızı ve kesme kuvvetleri gibi işlem parametrelerini anlamak için kullanılmıştır.
Moleküler dinamik algoritmaları[değiştir | kaynağı değiştir]
- Korunmuş Coulomb Potansiyelleri Örtük Solvent Modeli
Entegratörler[değiştir | kaynağı değiştir]
- Simplektik entegratör
- Verlet-Stoermer entegrasyonu
- Runge–Kutta entegrasyonu
- Beeman algoritması
- Kısıtlama algoritmaları (kısıtlı sistemler için)
Kısa menzilli etkileşim algoritmaları[değiştir | kaynağı değiştir]
- Hücre listeleri
- Verlet listesi
- Bağlı etkileşimler
Uzun menzilli etkileşim algoritmaları[değiştir | kaynağı değiştir]
- Ewald toplamı
- Parçacık ağı Ewald toplamı (PME)
- Parçacık - partikül - partikül ağı (P3M )
- Kaydırılmış kuvvet yöntemi
Paralelleştirme stratejileri[değiştir | kaynağı değiştir]
- Etki alanı ayrıştırma yöntemi (Paralel hesaplama için sistem verilerinin dağıtımı)
Ab-initio moleküler dinamik[değiştir | kaynağı değiştir]
- Car–Parrinello moleküler dinamiği
MD simülasyonları için özel donanım[değiştir | kaynağı değiştir]
- Anton - MD simülasyonlarını yürütmek için tasarlanmış uzman, devasa paralel bir süper bilgisayar
- MDGRAPE - Özellikle protein yapı tahmini için oluşturulmuş özel amaçlı bir moleküler dinamik simülasyonları sistemi
MD simülasyonları için bir donanım olarak grafik kartı[değiştir | kaynağı değiştir]
- GPU'da moleküler modelleme
Ayrıca bakınız[değiştir | kaynağı değiştir]
- Moleküler modelleme
- Bilgisayarlı kimya
- Kuvvet alanı (kimya)
- Güç alanı uygulamalarının karşılaştırılması
- Monte Carlo yöntemi
- Moleküler tasarım yazılımı
- Moleküler mekanik
- Çok Ölçekli Green fonksiyonu
- Car–Parrinello yöntemi
- Moleküler mekanik modelleme için yazılımın karşılaştırılması
- Kuantum kimyası
- Ayrık elemanlar yöntemi
- Nükleik asit simülasyon yazılımının karşılaştırılması
- Molekük editörü
Kaynakça[değiştir | kaynağı değiştir]
- ^ a b Fermi E., Pasta J., Ulam S., Los Alamos report LA-1940 (1955).
- ^ Jill P. Mesirov; Klaus Schulten; De Witt Sumners (29 Ağustos 1996). Mathematical Approaches to Biomolecular Structure and Dynamics (İngilizce). Springer Science & Business Media. ISBN 978-0-387-94838-6.
- ^ Endohedral confinement of a DNA dodecamer onto pristine carbon nanotubes and the stability of the canonical B form, 2014
- ^ Conformational Thermodynamics of DNA Strands in Hydrophilic Nanopores, 2016
Genel başvuru kaynakları[değiştir | kaynağı değiştir]
- M. P. Allen, D. J. Tildesley (1989) Computer simulation of liquids. Oxford University Press. 0-19-855645-4.
- J. A. McCammon, S. C. Harvey (1987) Dynamics of Proteins and Nucleic Acids. Cambridge University Press. 0-521-30750-3 (hardback).
- D. C. Rapaport (1996) The Art of Molecular Dynamics Simulation. 0-521-44561-2.
- M. Griebel; S. Knapek; G. Zumbusch (2007). Numerical Simulation in Molecular Dynamics. Berlin, Heidelberg: Springer. ISBN 978-3-540-68094-9.
- Frenkel, Daan; Smit, Berend (2002) [2001]. Understanding Molecular Simulation : from algorithms to applications. San Diego: Academic Press. ISBN 978-0-12-267351-1.
- J. M. Haile (2001) Molecular Dynamics Simulation: Elementary Methods. 0-471-18439-X
- R. J. Sadus, Molecular Simulation of Fluids: Theory, Algorithms and Object-Orientation, 2002, 0-444-51082-6
- Oren M. Becker, Alexander D. Mackerell, Jr., Benoît Roux, Masakatsu Watanabe (2001) Computational Biochemistry and Biophysics. Marcel Dekker. 0-8247-0455-X.
- Andrew Leach (2001) Molecular Modelling: Principles and Applications. (2nd Edition) Prentice Hall. 978-0-582-38210-7.
- Tamar Schlick (2002) Molecular Modeling and Simulation. Springer. 0-387-95404-X.
- William Graham Hoover (1991) Computational Statistical Mechanics, Elsevier, 0-444-88192-1.
- D. J. Evans and G. P. Morriss (2008) Statistical Mechanics of Nonequilibrium Liquids, Second Edition, Cambridge University Press, 978-0-521-85791-8.
- Bou-Rabee, Nawaf (2014). "Time Integrators for Molecular Dynamics". Entropy. 16 (1). ss. 138-162. Bibcode:2013Entrp..16..138B. doi:10.3390/e16010138.
Dış bağlantılar[değiştir | kaynağı değiştir]
- GPUGRID.net Projesi23 Eylül 2019 tarihinde Wayback Machine sitesinde arşivlendi. (GPUGRID.net )
- Mavi Gen Projesi (IBM ) JawBreakers.org
- Malzeme modelleme ve bilgisayar simülasyon kodları25 Eylül 2019 tarihinde Wayback Machine sitesinde arşivlendi.
- Moleküler dinamiği hakkında birkaç ipucu26 Eylül 2019 tarihinde Wayback Machine sitesinde arşivlendi.
- MD su simülasyonu filmi (Youtube)23 Mart 2019 tarihinde Wayback Machine sitesinde arşivlendi.
- Saniyede 1 kare görüntülenen canlı moleküler dinamik simülasyonu19 Eylül 2019 tarihinde Wayback Machine sitesinde arşivlendi.


