Ergodik kuramı
Fizik ve termodinamikte, ergodik kuramı,[1] uzun bir zaman periyodunda, bir sistemin aynı enerji ile mikro istasyonların faz uzayının bir bölümünde geçirdiği zamanın, bu bölgenin hacmiyle orantılı olduğunu, yani, erişilebilir tüm mikrostatların uzun süre boyunca eşgüdümlü olmasıdır.

Liouville Teoremi, Hamilton sistemleri için, faz uzayı boyunca bir parçacık yolunu takiben mikro istasyonların yerel yoğunluğunun, toplulukla birlikte hareket eden bir gözlemcinin (yani, konvivektif zaman türevi sıfır) bakıldığında sabit olduğunu belirtmektedir. Böylece, eğer mikrostatlar ilk başta faz alanına eşit olarak dağıtılırsa, her zaman öyle kalacaktır. Fakat Liouville teoremi ergodik hipotezin tüm Hamilton sistemleri için geçerli olduğunu ima etmez.
Ergodik hipotez genelde hesaplama fiziğinin istatistiksel analizinde varsayılmaktadır. Analist, süreç parametrelerinin zaman içindeki ortalama ve istatistiksel topluluktaki ortalamanın aynı olduğunu varsayabilir. Bir sistemin aynı sistemin birçok bağımsız gerçekleşmesi için olduğu kadar uzun süre taklit edilmesi iyi olduğu varsayımı her zaman doğru değildir. (Bakınız, örneğin, 1953 Fermi-Makarna-Ulam-Tsingou deneyi.)
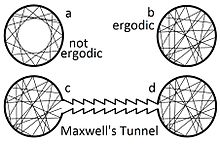
Ergodik hipotezin varsayımı, ikinci çeşit sürekli hareketli makinelerin bazı türlerinin imkânsız olduğunun kanıtlanmasına izin verir. Yukarıdaki şekil ergodik hipotezin ideal bir gazın basit bir modeli için geçerli olduğu ve tutmadığı durumları göstermektedir. Duvarlar mükemmel pürüzsüz ve daireseldir, ergodik hipotez tutulmaz. Speküler yansımaların atomların daha az nüfuslu bir kaptan daha yoğun bir şekilde özdeş olana taşınmasına neden olan bir tür tünel oluşturmak mü[2] mkün olsaydı, rastgele termal enerjinin gereksiz bir şekilde faydalı işe dönüştürülmesine izin verirdi bir ısı banyosu. Fakat, Liouville teoremi ile faz uzayının tüm bölgeleri zaman içinde eşit olarak doldurulursa, t = 0 ise, o zaman tüm zaman boyunca eşit derecede muhtemel olurlar. Yansıtıcı "tuzak" veya Maxwell ilişkileri (şekilde gösterilen gibi), her iki kapta da eşit yoğunluk ve basınçta rastgele dolaşan bir gazın "karışıklığını" bozmayacaktır.
Fenomenoloji[değiştir | kaynağı değiştir]
Makroskopik sistemlerde, bir sistemin kendi faz uzayının tamamını gerçekten keşfedebildiği zaman çizelgeleri, termodinamik denge durumunun bir miktar ergodisite kırılması sergilemesi için yeterince büyük olabilir. Genel bir örnek Curie sıcaklığı altında, sistem tercihen sıfır olmayan bir manyetizasyonu almasını sağlar ferromanyetik sistemlerde kendiliğinden manyetizasyon ait ergodic hipotez net bir manyetizasyon zamana tüm durumları keşfetmek sistemi sayesinde bulunması gerektiğini ima halde olmasıdır ortalama manyetizasyon sıfır olmalıdır. Makroskopik sistemlerin sıklıkla ergodik hipotezin gerçek şeklini ihlal etmesi, spontan bir simetri kırılmasına bir örnektir.
Bununla birlikte, eğirme camı gibi kompleks düzensiz sistemler, pratikte görülen termodinamik denge durumunun simetri argümanları tarafından tahmin edilmesi daha zor olan ergodisite kırılmasını daha da karmaşık bir biçimde göstermektedir. Ayrıca, geleneksel camlar (örneğin cam gözlükleri), ergodikliği karmaşık bir tarzda ihlal etmektedir. Uygulamada, bu, yeterince kısa zaman ölçeklerinde (örneğin saniye, dakika veya birkaç saatlik kısımlarınki) sistemlerin katı olarak, yani pozitif bir kayma modülü ile, fakat son derece uzun ölçeklerde, örn. binlerce yıldır ya da sıvı olarak ya da iki ya da daha fazla zaman ölçeğidir.
Matematik[değiştir | kaynağı değiştir]
Ergodik teori, bu hipotezin bir versiyonunu karşılayan dinamik sistemler ile uğraşan, ölçüm teorisinin dilinde dile getirilen, matematiğin bir koludur.
Kaynakça[değiştir | kaynağı değiştir]
- ^ Ludwig Boltzmann. "Ergodik kuramı". J. A. Barth, 1898. 20 Ocak 2018 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Aralık 2017.
- ^ http://adsabs.harvard.edu/abs/1982AdPhy..31..669P [yalın URL]
