Kutupsal koordinat sistemi

Matematikte kutupsal koordinat sistemi veya polar koordinat sistemi, noktaların birer açı ve Kartezyen koordinat sistemindeki orijinin eşdeğeri olup "kutup" olarak bilinen bir merkez noktaya olan uzaklıklar ile tanımlandığı, iki boyutlu bir koordinat sistemidir. Kutupsal koordinat sistemi, matematik, fizik, mühendislik, denizcilik, robot teknolojisi gibi birçok alanda kullanılır. Bu sistem, iki nokta arasındaki ilişkinin açı ve uzaklık ile daha kolay ifade edilebildiği durumlar için özellikle kullanışlıdır. Kartezyen koordinat sisteminde, böyle bir ilişki ancak trigonometrik formüller ile bulunabilir. Kutupsal denklemler, çoğu eğri tipi için en kolay, bazıları içinse yegâne tanımlama yöntemidir.
Tarihçe[değiştir | kaynağı değiştir]
Antik Yunan uygarlığı'nda açı ve yarıçap kavramlarının kullanıldığı bilinmektedir. (MÖ 190 - 120), her açı için kiriş uzunluklarını veren bir kiriş fonksiyonları tablosu oluşturulmuştur ve yıldızların konumlarını belirlemek için kutupsal koordinatlar kullandığına ilişkin kaynaklar bulunmaktadır.[1] "Spiraller Üzerine" (On Spirals) adlı eserinde Arşimet, ünlü spiralini yarıçapın açıya bağlı olduğu bir fonksiyon olarak tanımlar. Bununla beraber, Yunan çalışmaları, koordinat sistemini tam olarak tanımlayamamıştır.
Kutupsal koordinatları resmî bir koordinat sisteminin parçası olarak ilk olarak kimin tanımladığına ilişkin farklı söylemler vardır. Konunun tarihçesi, Harvard profesörü Julian Lowell Coolidge'in "Kutupsal Koordinatların Kaynağı" (Origin of Polar Coordinates) adlı kitabında anlatılmıştır.[2][3] Grégoire de Saint-Vincent ve Bonaventura Cavalieri yaklaşık aynı zamanda birbirinden bağımsız olarak kavramları oluşturmaya başlamıştır. Saint-Vincent, çalışmalarını 1625 yılında yazmış ve 1647 yılında yayınlamışken, Cavalieri de 1635 yılında kendi çalışmalarının ilk baskısını yapıp 1653 yılında elden geçirilmiş bir sürümünü yayınlamıştır. Bir Arşimet spirali içindeki alanla ilgili bir problemin çözümünde kutupsal koordinat sisteminden ilk yararlanan Cavalieri olmuştur. Daha sonra Blaise Pascal, parabolik yayların uzunluğunu hesaplamak için kutupsal koordinatları kullanmıştır.
1671 yılında yazılmış ve 1736 yılında basılmış olan Method of Fluxions çalışmasıyla Isaac Newton, kutupsal koordinatlara bir düzlemdeki herhangi bir noktanın yerini saptama yöntemi olarak bakan ilk kişi olmuştur. Newton, kutupsal koordinatlar ve diğer dokuz koordinat sistemi arasındaki dönüşümleri incelemiştir. Acta eruditorum (1691) adlı çalışmasında Jacob Bernoulli, sırasıyla kutup ve kutupsal eksen olarak adlandırdığı bir nokta ve o noktanın üzerinde yer aldığı eksenden oluşan bir sistem kullanmıştır. Bu sistemde koordinatlar, kutba göre uzaklık ve kutup eksenine göre açı ile belirtilmiştir. Bernoulli'nin çalışması, bu koordinatlarla tanımlanmış eğrilerin eğim yarıçaplarını hesaplamaya kadar ilerlemiştir.
Gregorio Fontana'ya atfedilmiş olan kutupsal koordinatlar terimi, 18. yüzyıl İtalyan yazarları tarafından kullanılmıştır. Terimin İngilizce yayınlarda ilk yer alışı, George Peacock'ın Sylvestre François Lacroix'ya ait "Diferansiyel ve İntegral Hesaplamalar" (Differential and Integral Calculus) adlı kitabını çevirmesi ile 1816 yılında olmuştur.[4][5][6]
Alexis Clairaut ve Leonhard Euler, kutupsal koordinat kavramının üç boyuta uyarlanmasında rol oynamışlardır.
Kutupsal koordinatlar ile noktaların belirtilmesi[değiştir | kaynağı değiştir]

Tüm iki boyutlu koordinat sistemlerinde olduğu gibi, kutupsal koordinat sisteminde de iki koordinat vardır: r ("radyal koordinat" ya da "ışınsal koordinat") ve θ ("açısal koordinat", "kutupsal açı" ya da "yatay açı"; bazen φ veya t ile gösterilir). r koordinatı, kutuptan olan ışınsal uzaklığı; θ koordinatı ise noktanın üzerinde bulunduğu ışının, bazen "kutupsal eksen" de denilen 0° ışınından saat yönünün tersi yönündeki açısını ifade eder. 0° ışını, Kartezyen koordinat sisteminde "pozitif x ekseni" olarak bilinir.[7]
Örneğin, kutupsal koordinatları (3, 60°) olan bir nokta, kutupsal eksene 60° açı ile duran ışın üzerinde kutuptan 3 birim uzaklıkta bulunur. Koordinatları (-3, 240°) olan nokta da aynı yerde gösterilecektir çünkü bir negatif ışınsal uzaklık, karşıt ışın üzerinde pozitif uzaklık olarak ölçülür (240° − 180° = 60°).
Kutupsal koordinat sisteminin Kartezyen koordinat sisteminde bulunmayan bir önemli özelliği, belli bir noktanın sonsuz sayıda farklı koordinat ile belirtilebilmesidir. Genel olarak, n herhangi bir tam sayı olmak üzere, herhangi bir (r, θ) noktası (r, θ ± n×360°) veya (−r, θ ± (2n + 1)180°) olarak gösterilebilir.[8] Eğer bir noktanın r koordinatı 0 ise, o nokta θ koordinatından bağımsız olarak kutup üzerinde bulunur.
Radyan ölçüsünün kullanımı[değiştir | kaynağı değiştir]
Kutupsal sistemde açılar, genel olarak ya derece ya da radyan cinsinden ifade edilir ve bunun için de 2π rad = 360° dönüşümü kullanılır. Seçim çoğunlukla ihtiyaca bağlıdır. Denizcilik uygulamalarında derece ölçüsü kullanılırken, özellikle dönüş mekaniği gibi bazı fizik uygulamalarında ise dairenin çevresinin (c) yarıçapına (r) oranına dayanan radyan ölçüsü kullanılır (c = 2πr).[9]
Kutupsal ve kartezyen koordinatlar arası dönüşüm[değiştir | kaynağı değiştir]
Kutupsal koordinatlar r ve θ, kartezyen koordinatlara şu şekilde dönüştürülebilir.
Bu iki formüle göre x ve y cinsinden elde edilen dönüşüm formülleri ise şöyledir:
Eğer x = 0 ve
- y pozitifse, θ = 90° (π/2 rad);
- y negatifse, θ = 270° (3π/2 rad) olur.
Kutupsal denklemler[değiştir | kaynağı değiştir]
Kutupsal koordinatlar ile ifade edilmiş bir eğri denklemi "kutupsal denklem" olarak bilinir ve genellikle r, θ'nın bir fonksiyonu olarak yazılır.
Kutupsal denklemler değişik simetri biçimleri gösterebilir. Bir eğri,
- eğer r(−θ) = r(θ) ise 0°/180° yatay ışınına göre,
- eğer r(π−θ) = r(θ) ise 90°/270° dikey ışınına göre ve
- eğer r(θ−α) = r(θ) ise saat yönünün tersinde, rotasyonel (dönel) olarak kutup noktasına göre α° kadar simetrik olacaktır.[10]

Çember[değiştir | kaynağı değiştir]
Merkezi (r0, φ) noktasında ve yarıçapı a olan herhangi bir çemberin genel denklemi şu şekildedir:
Bu denklem özel durumlar için çeşitli yollarla basitleştirilebilir. Örneğin
- ,
merkezi kutup noktasında ve yarıçapı a olan çember için yazılmış denklemdir.[11]
Doğru[değiştir | kaynağı değiştir]
Kutuptan geçen ışınsal doğrular şu denklemle gösterilir:
Burada φ, doğrunun eğim açısıdır ve m'nin Kartezyen koordinat sistemindeki eğimi temsil ettiği
denklemi ile de ifade edilebilir.
Kutup noktasından geçmeyen herhangi bir doğru, ışınsal bir doğruya diktir.[12] θ = φ doğrusunu (r0, φ) noktasında dik kesen doğrunun denklemi ise şöyledir:
- .

Kutupsal gül[değiştir | kaynağı değiştir]
Kutupsal gül, taç yapraklı bir çiçeği andıran ve sadece kutupsal bir denklem ile ifade edilebilen ünlü bir matematiksel eğridir. Şu denklemlerle tanımlanır:
- veya
a değişkeninin gülün yapraklarının uzunluğunu ifade ettiği bu denklemlerde eğer k bir tam sayı ise, k tek sayı olduğunda bu denklemler ile k-yapraklı bir gül ve çift sayı olduğundaysa 2k-yapraklı bir gül elde edilir. Eğer k tam sayı değilse, yaprak sayısı da tam sayı olmayacağı için, bir daire şekli oluşur. Dikkat edilmesi gereken nokta, bu denklemlerle 4'ün katlarının 2 fazlası (2, 6, 10, 14, ...) kadar sayıda taç yaprak elde etmenin mümkün olmadığıdır.

Arşimet spirali[değiştir | kaynağı değiştir]
Arşimet spirali, Arşimet tarafından keşfedilmiş ve gene yalnızca bir kutupsal denklem ile tanımlanabilen, ünlü bir spiraldir. Şu denklemle ifade edilir:
- .
a değişkeninin değişimi spirali döndürürken, b değişkeni spiralin kolları arasındaki daima sabit olan uzaklığı kontrol eder. Arşimet spirali, θ > 0 ve θ < 0 değerleri için iki kola sahiptir. İki kol kutup noktasında birbirine düzgün biçimde bağlanır. Kollardan birinin 90°/270° doğrusu üzerinden ayna simetrisi alınırsa, diğer kol elde edilir.
Konik kesitler[değiştir | kaynağı değiştir]

Büyük ekseni kutupsal eksen (0° ışını) üzerinde, bir odağı kutup noktasında ve diğer odağı da kutupsal eksen üzerindeki başka bir noktada bulunan bir konik kesit şu kutupsal denklem ile tanımlanır:
- .
Burada e eksantriklik ve l de (semi-latus rectum) büyük eksene dik olarak bir odaktan eğriye kadar ölçülen uzaklıktır. Denklem; e > 1 ise bir hiperbol, e = 1 ise bir parabol ve e < 1 ise bir elips oluşturur. e < 1 koşulunun özel bir durumu olarak e = 0 ise, yarıçapı l olan bir çember elde edilir.
Diğer eğriler[değiştir | kaynağı değiştir]
Kutupsal koordinat sisteminin dairesel özelliği, birçok eğrinin Kartezyen biçimdense kutupsal bir denklemle çok daha kolay tanımlanmasını sağlar. Bu eğrilerin arasında lemniskatlar, ilmek eğrileri (limaçonlar) ve özel bir tip limaçon olan kardiyoidler vardır.
Calculus (analiz)[değiştir | kaynağı değiştir]
Kutupsal koordinatlar ile ifade edilmiş denklemlere kalkulus (diferansiyel ve integral hesaplamalar) uygulanabilir.[13][14]
Diferansiyel hesaplama[değiştir | kaynağı değiştir]
Bir r(θ) kutupsal eğrisine herhangi bir noktasından teğet olan doğrunun Kartezyen eğimini bulmak için, eğri öncelikle parametrelere bağlı bir denklem sistemi ile tanımlanır:
Sonra, bu denklemlerin θ'ya göre türevlerinin alınmasıyla şu denklemler elde edilir:
Birinci denklemin ikinciyle bölünmesi sonucunda da eğriye (r, r(θ)) noktasında teğet olan doğrunun Kartezyen eğimine ait denklem elde edilir:
İntegral hesaplama[değiştir | kaynağı değiştir]
0 < b − a < 2π olmak üzere, r(θ) eğrisinin [a, b] kapalı aralığında kalan kısmının altında kalan alanı bulmak için, öncelikle eğri bir Riemann toplamı olarak tanımlanır.
- İlk olarak, [a, b] aralığı n kadar alt aralığa bölünür (burada n, isteğe bağlı seçilmiş pozitif bir tam sayıdır). Böylece, her alt aralığın uzunluğunu temsil eden Δθ, aralığın tüm uzunluğunun (b − a) alt aralık sayısına (n) bölümüne eşit olur.
- Her i = 1, 2, …, n alt aralığı için θi'nin alt aralığın orta noktası olduğu kabul edilir ve merkezi kutupta, yarıçapı r(θi) ve merkezî açısı Δθ olan birer sektör çizilir.
- Buna göre, çizilmiş her sektörün alanı şu denklemle verilebilir:
- Dolayısıyla, tüm sektörlerin toplam alanı da altta sunulan denklemle tanımlanır:
n alt aralıklarının sayısı ne kadar artarsa, söz konusu alanın ölçümü de gerçek alana o kadar çok yaklaşır. Böylece, [a, b] aralığındaki r(θ) eğrisinin altında kalan alan söyle tanımlanabilir:
Bu ifade, aşağıdaki integralin Riemann toplamıdır:
Vektörel hesaplamalar[değiştir | kaynağı değiştir]
Hesaplamalar, denklemlerin kutupsal koordinatlar içinde ifade edilmesi ile bu koordinatlarda uygulanabilir. , r ve t zamanına bağlı olmak üzere pozisyonundaki vektör olsun, , yönündeki birim vektör ve , için uygun açılardaki birim vektör olsun. Konumun birinci ve ikinci türevleri şunlardır:
- .
eğri üzerindeki bir noktayı odak alarak çizilen çizginin süpürdüğü alan olarak alındığında, limit içinde , ve tarafından şekillendirilmiş paralelkenar alanının yarısıdır,
- ,
ve toplam alan 'nın zamana göre integralinin alınması ile bulunur.
Üç boyut[değiştir | kaynağı değiştir]
Kutupsal koordinat sistemi, biri silindrik koordinat sistemi ve diğeri de küresel koordinat sistemi olmak üzere, iki farklı koordinat sistemi ile üç boyuta genişletilir. Her iki sistem de iki boyutlu kutupsal koordinatları bir alt küme olarak kullanır.
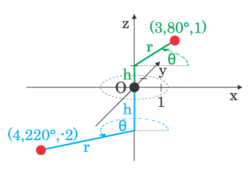
Silindirik koordinatlar[değiştir | kaynağı değiştir]
Silindirik koordinat sistemi, düzlemden ayrı duran bir noktanın düzleme olan yüksekliğini ölçebilecek üçüncü bir koordinatı iki boyutlu kutupsal koordinat sistemine ekleyerek elde edilir. Bu, kartezyen koordinat sistemini üç boyuta genişletmek için kullanılana benzer bir yöntemdir. İki boyutlu kutupsal koordinat düzlemine dik duran ve kutup noktasından geçen üçüncü koordinat, genellikle h ile gösterilir dikdüzlemine Üçüncü koordinat genelde h ile gösterilir. Buna göre de üç silindirik koordinat, (r, θ, h) yazımı ile ifade edilir.
Silindirik koordinatların Kartezyen koordinatlara dönüşümü şu şekilde olur:

Küresel koordinatlar[değiştir | kaynağı değiştir]
Kutupsal koordinatlar, (ρ, φ, θ) koordinatları kullanılarak da üç boyuta genişletilebilir. Burada;
- ρ, kutup noktasından olan uzaklık,
- φ, z ekseninden olan açı ("eş enlem" (colatitude) ya da "zirve" (zenith) de denir; 0'dan 180°'ye kadar ölçülür) ve
- θ da kutupsal koordinatlardaki gibi, x ekseninden olan açıdır.
"Küresel koordinat sistemi" olarak adlandırılan bu sistem, Dünya için kullanılan enlem ve boylam sistemine benzerdir:
- enlem, φ'nin tümleyicisidir ve δ = 90° − φ eşitliğiyle belirlenir;
- boylam da l = θ − 180° ile saptanır.[15]
Küresel koordinat sistemini oluşturan üç koordinatın, Kartezyen sisteme dönüşümü şu şekildedir.
- hda
Uygulamalar[değiştir | kaynağı değiştir]
Robot bilimi[değiştir | kaynağı değiştir]
Hareket edebilen çoğu robot, seyir için kutupsal koordinat sistemini ya da onun biraz değiştirilmiş hâlini kullanır. Bu yapay zekâ için çok uygundur çünkü koordinat sisteminin merkezini (kutbunu) daima robotun o andaki konumu oluşturur. Dolayısıyla, robotun herhangi bir zamanda koordinat sisteminin neresinde olduğunu hesaplamasına gerek yoktur: tek gereken, hangi yönde ve ne kadar uzağa gideceğini belirlemesidir. Eğer robotlar kartezyen koordinat sistemini kullanarak yol alsalardı, hareket için gerekli uzaklık ve açı hesaplamaları için cebir ve trigonometri kullanmak gerekirdi. Oysa, kutupsal koordinat sistemindeki bir açı ile ifade edilen yön ile katedilmesi gereken uzaklık bilgisi, robotun tam istenen yere gitmesini sağlamak için yeterlidir.
Havacılık[değiştir | kaynağı değiştir]
Havalanan uçaklar, seyir için kutupsal koordinat sisteminin biraz değiştirilmiş bir çeşidini kullanırlar. Bu sistemde, genellikle "yön 360" (heading 360) olarak adlandırılan 0° ışını dikeydir ve açılar saatin tersi yönde değil, saat yönünde devam eder. Yön 360 manyetik kuzeye denk gelirken, 90, 180 ve 270 yönleri de sırasıyla manyetik doğu, güney ve batıya denk gelir.[16] Dolayısıyla, örneğin doğuya doğru 5 deniz mili kadar yol alacak bir uçak, yön 90 üzerinde 5 birim katedecek demektir.[17]

Arşimet spirali[değiştir | kaynağı değiştir]
Arşimet spiralinin gerçek dünyada pek çok uygulaması vardır.
Örneğin, Arşimet spirali şekilli ve birbirinin içine geçmiş aynı büyüklükteki iki sarmal, sıvı ya da gaz gibi akışkanları pompalamak ya da sıkıştırmak için kullanılan sarmal kompresörlerin temelini oluşturur. Sarmallardan biri sabit dururken, diğeri kendi çevresinde dönmemek üzere merkez dışı (eksantrik) bir dönüş hareketi yapar ve akışkanı iki sarmalın duvarları arasında sıkıştırarak ilerletir.
Gramofon plakların çok erken dönemlerinde, plak üzerindeki oluklar bir Arşimet spirali oluşturacak şekilde açılır ve bu şekilde, olukların birbirlerinden eş uzaklıkta durmaları sağlanarak, bir plağın üstüne en çok miktarda müzik kaydedilmeye çalışılırdı. Ancak sonraları, daha iyi ses kalitesi elde edebilmek için bu uygulamadan vazgeçilmiştir.
Kepler'in gezegensel hareket kanunları[değiştir | kaynağı değiştir]

Kutupsal koordinatlar, Kepler'in gezegensel hareket kanunları için doğal bir ifade yöntemi sağlar.
Kepler'in birinci kanununa göre, bir yıldız çevresindeki bir gezegenin yörüngesi, bir odağı sistemin kütle merkezinde oturan bir elipstir. Bu elipsi ifade etmek için, yukarıdaki "Konik kesitler" bölümünde verilmiş olan denklem kullanılabilir.
Kepler'in ikinci kanunu olan "eşit alanlar kanunu" ise şunu söyler: "bir gezegen ile onun yıldızını birleştiren bir doğru, eşit zaman aralıklarında birbirine eşit alanlar tarar"; yani, sabittir. Bu denklemler Newton'un hareket kanunlarından elde edilebilir ve kutupsal koordinatların kullanıldığı tam bir türetme, Kepler'in gezegensel hareket yasaları maddesinde sunulmuştur.
Ayrıca bakınız[değiştir | kaynağı değiştir]
Diğer koordinat sistemleri[değiştir | kaynağı değiştir]
- Koordinat sistemi
- Kartezyen koordinat sistemi
- Silindirik koordinat sistemi
- Eğrisel koordinatlar
- Ortogonal koordinatlar
- Eliptik koordinatlar
- Hiperbolik koordinatlar
- Stereografik izdüşüm
- Paralel koordinatlar
- Yermerkezli koordinatlar
Kaynakça[değiştir | kaynağı değiştir]
- ^ Friendly, Michael. "Milestones in the History of Thematic Cartography, Statistical Graphics, and Data Visualization". 20 Mart 2011 tarihinde kaynağından arşivlendi.
- ^ "The MacTutor History of Mathematics archive: Coolidge's Origin of Polar Coordinates". 1 Haziran 2006 tarihinde kaynağından arşivlendi. Erişim tarihi: 24 Kasım 2006.
- ^ Coolidge, Julian Lowell (1952). "The Origin of Polar Coordinates". American Mathematical Monthly. Cilt 59. ss. 78-85.
- ^ Daniel Klaasen. Historical Topics for the Mathematical Classroom.
- ^ Miller, Jeff. "Earliest Known Uses of Some of the Words of Mathematics". 19 Temmuz 2008 tarihinde kaynağından arşivlendi.
- ^ Smith, David Eugene (1925). History of Mathematics, Vol II. Ginn and Co.
- ^ Brown, Richard G. (1997). Advanced Mathematics: Precalculus with Discrete Mathematics and Data Analysis. McDougal Littell Inc. ISBN 0-395-77114-5.
- ^ "Polar Coordinates and Graphing" (PDF). 13 Nisan 2006. 15 Şubat 2012 tarihinde kaynağından (PDF) arşivlendi.
- ^ Serway, Raymond A. ve Jewett, Jr., John W. (2005). Principles of Physics. Brooks/Cole—Thomson Learning. ISBN 0-534-49143-X.
- ^ a b "Mathworld-Polar Coordinates". 28 Ekim 2006 tarihinde kaynağından arşivlendi. Erişim tarihi: 24 Kasım 2006.
- ^ "Polar coordinates". 5 Ağustos 2015 tarihinde kaynağından arşivlendi.
- ^ Ward, Robert L. "Analytic Geometry: Polar Coordinates". 4 Ağustos 2015 tarihinde kaynağından arşivlendi.
- ^ Lawrence S. Husch. "Areas Bounded by Polar Curves". 11 Ekim 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 25 Kasım 2006.
- ^ Lawrence S. Husch. "Tangent Lines to Polar Graphs". 2 Temmuz 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 25 Kasım 2006.
- ^ Wattenberg, Frank (1997). "Spherical Coordinates". 16 Mayıs 2013 tarihinde kaynağından arşivlendi.
- ^ "Aircraft Navigation System". 8 Temmuz 2015 tarihinde kaynağından arşivlendi.
- ^ "Air Traffic Control". 12 Temmuz 2007 tarihinde kaynağından arşivlendi.








































