Doğrusal denklem dizgesi

Doğrusal denklem dizgesi, birkaç tane aynı tip değişkenleri içeren birkaç tane doğrusal denklemlerin oluşturduğu topluluktur. Örneğin:
Burada üç çeşit değişken , ile bulunur ve bu üç değişken üç ayrı doğrusal denklem içindedir ve böylece doğrusal denklemler (sistemi) dizge elde edilir.
Bir doğrusal dizgenin çözümü bilinmeyen değişkenlere, tüm doğrusal denklemleri aynı zamanda tatmin eden, reel sayıların tahsis edilmesidir. Yukarıdaki denklemler dizgesi için çözüm kümesi bulunur ve bu
olur.
Doğrusal denklem dizgeleri mühendislik, fizik, kimya, bilgisayar bilimi ve ekonomide pek çok uygulama alanı bulur.
Genel şekil[değiştir | kaynağı değiştir]
n bilinmeyen değişkenli m sayıda doğrusal denklemden oluşan bir doğrusal denklen dizgesi genel olarak şöyle yazılabilir:
Burada n-tane bilinmeyen değişkendir. bu değişkenlerin katsayılarıdır. Her katsayının altında bulunan ilk sayı denklem sayısına ve ikincisi değişken tipinin sayısına tekabül eder; örneğin üçüncü denklemdeki birinci değişken 'in katsayısıdır. terimleri ise her denklem için sabit terimleri verir.
Çok kere katsayılar ve bilinmeyen değişkenler reel sayılardır. Fakat ileri matematikte bunlar karmaşık sayılar, tam sayılar, polinomlar ve hatta soyut cebirsel yapılar bile olabilirler.
Vektör denklemi[değiştir | kaynağı değiştir]
Bu genel doğrusal denklemler dizgesini uygun bir şekilde ifade edilmesi vektörler halinde olur: Bu ifade şeklinde her bir değişken bir doğrusal bileşimde bir ağırlık olarak bir sütun vektör ile ifade edilmektedir.
Matris denklemi[değiştir | kaynağı değiştir]
Vektör denklemine aynen tekabül eden ve matriks kullanılarak ifade edilen genel doğrusal denklemler dizgesi şu şekilde ifade edilir:
burada A m×n matrisi, x içinde n tane ifade bulunan bir sütun vektörü ve b içinde m tane sabit ifade olan bir sütun vektörü olur.
Çözüm kümesi[değiştir | kaynağı değiştir]

Bir doğrusal denklem dizgenin çözümü, bilinmeyen değişkenlere (yani x1, x2, ..., xn değişkenlerine) tüm doğrusal denklemleri aynı zamanda tatmin eden reel sayısal değerler tahsis edilmesidir. Tüm mümkün çözümlerin bir matematiksel kümesine çözüm kümesi adı verilir.
Bir doğrusal denklem dizgesi için üç ve sadece alternatif mümkün sonuç ortaya çıkabilir:
- Sistemin sonsuz sayıda çeşitli çözümü bulunur;
- Sistemin tek bir çözümü bulunur;
- Sistemin hiçbir çözümü bulunmaz.
Geometrik yorum[değiştir | kaynağı değiştir]
İki değişkenden ( ve ) oluşan bir dizge için her bir denklem ve eksenli dikdörtgen koordinat sıstemi grafiği içinde bir doğru ile gösterilir. Bir çözüm dizgedeki tüm denklemleri tatmin etmesi gerektiği için, çözüm kümesi bu doğruların kesişme noktasıdır veya tek bir doğru ya tek bir nokta ya da boş küme olarak görülür.
Üç değişkenli bir dizge için her doğrusal denklem üç boyutlu bir uzayda bir düzlem olurlar ve çözüm kümesi bu düzlemlerin kesişmesidir. Böylece çözüm kümesi ya bir düzlem, ya tek bir doğru, ya tek bir nokta ya da boş küme olur.
n sayıda değişken halinde, her bir doğrusal denklem bir n-boyutlu uzayda bir hiperdüzlem olarak ortaya çıkar. Çözüm kümesi bu hiperdüzlemlerin kesişmeleridir ve n-ye kadar herhangi bir boyutta düzlük olabilir.
Genel sonuç hali[değiştir | kaynağı değiştir]

Genel olarak, bir doğrusal denklemler dizgesinin sonucunun ne olabileceği, denklemler sayısı ile bilinmeyen değişkenler sayısı arasındaki bağlantılar tarafından belirlenir:
- Genellikle, eğer dizgede denklem sayısı bilinmeyen değişken sayısından daha küçükse ise, dizge için sonsuz sayıda çözüm bulunur. Fakat bazen tek bir "seyrek çözüm" bulma imkânı da vardır. Yani kullandığımız notasyona göre m < n ise, sonsuz çözüm vardır. Bu çeşit dizgelere kararsız dizge (underdetermined system) adı verilir.
- Genellikle, eğer dizgede denklem sayısı değişken sayısı ile aynı ise, tek bir tane çözüm bulunur; yani m = n ise tek ve tek bir çözüm bulunur.
- Genellikle, eğer dizgede denklem sayısı değişken sayısıdan daha büyük ise hiçbir sçözüm bulunmaz; yani m > n ise hiçbir çözüm bulunmaz.
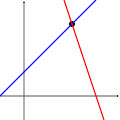
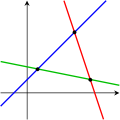
Aşağıdaki gösterimler iki değişkenli halde ortaya çıkabilmesi mümkün üçlü sonucu göstermektedir:
Verilen gösterimede; birinci dizgenin sonsuz sayıda çözümü bulunur; yani bunun noktaları mavi renkli doğru üzerindedir. İkinci dizgede tek bir çözüm bulunur; yani iki doğrunun kesişme noktası çözümdür. Üçüncü sistemde bulunan üç doğrunun ortaklaşa hiçbir noktaları bulunmaz.
Fakat şunu unutmamak gerekir; bütün bu sonuçlar sadece genellikle doğrudur. İki denklemeli ve iki değişkenli bir dizgenin hiçbir çözümü olmaması mümkündür; bu hal her iki doğru birbirine paralel ise ortaya çıkar. Üç denklemle iki değişkenli bir dizgenin çözümü olması mümkündür; bu hal eğer üç doğru birbiriyle tek noktada kesişirlerse ortaya çıkar. Genel olarak; bir doğrusal denklemler dizgesi beklenenden değişik davranış göstermesi eğer denklemler "doğrusal olarak bağımlı" iseler veya iki veya daha çok sayıda denklemlerin "tutarsız" olmaları halinde ortaya çıkar.
Nitelikler[değiştir | kaynağı değiştir]
Bağımsızlık[değiştir | kaynağı değiştir]
Bir doğrusal denklem dizgesinin denklemleri bağımsızlık niteliği, dizgede bulunan denklem eşitliklerinin hiçbiri denklemden cebirsel olarak çıkartılaması halidir. Eğer denklemler bağımsızlarsa, her bir denklem değişkenler hakkında yeni bilgi kapsamaktadır ve bu denklemlerden herhangi birinin ortadan kaldırılması çözüm kümesinin boyutunu artır. Doğrusal denklemler için mantıksal bağımsızlık doğrusual bağımsızlık özelliğiyle ile aynıdır.
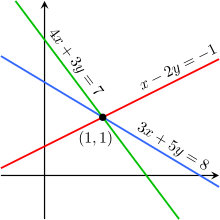
Örneğin, şu denklemler
bağımsız değildirler; çünkü ikinci denklem birinci denklemin 2 ile çarpımı ile elde edilmiştir ve eğer bu iki denklem için grafik çizilirse iki doğru üste çakışıp tek bir doğru görüntüsü verirler.
Daha karmaşık bir örnek için verilen denklemler dizgesi şu olsun:
Bu üç denklem dizgesi bağımsız değildir, çünkü üçüncü denklem ilk iki denklemin birbirine toplamından elde edilmiştir. Gerçekten bu üç denklemden herhangi ikisinden üçüncü denklem çıkartılabilir ve bu üç denklemden herhangi tek bir tanesi ortadan kaldırılırsa çözüm kümesi hiç değişmeden aynı kalır. Bu üç doğru için grafik üçü de tek bir noktada kesişen üç doğru şeklindedir.
Tutarlılık[değiştir | kaynağı değiştir]
Bir doğrusal denklemler dizgesi denklemleri, eğer bir ortak çözüm varsa, "tutarlı" olur; aksi halde "tutarsız" olur. Eğer denklemler tutarlı iseler; denklemlerden bir çelişkilik ortaya çıkartmak imkânı bulunur; örneğin 1 = 3 ifadesi gibi.
Örneğin şu denklemler
tutarsızdır. Bir çözüm bulmaya çalışmak için, söylenmeden anlaşılan "bir çözüm vardır" varsayımını yapmaktayız. Diğer bir ifade ile, birinci denklemmde bulunan değerinin ikinci denklemde bulunan değeri ile aynı açıkça olduğunu açıkça söylemeden varsaymaktayız (ve aynı şekilde ve aynı zamanda her iki denklemde de aynı varsayımı yapıyoruz.) ( ıcın ikame ediliebilirlik özelliğini uyguluyarak 6 = 12 olarak bir denklem buluruz ve bu da yanlış bir ifadededir. Bu hatalı ifade dizgenin bir çözümü olduğuna dair yaptımız varsayım ile çelişmektedir ve bundan dolayı varsayımımızın yanlış olduğu sonucu çıkmaktadır; yani doğrusal denklemler dizgesinin "hiçbir çözümü bulunmaz". Bu denklemlerin düzeyindeki grafikleri birbirine parallel iki doğru halindedir.
Üç doğrusal denklemli dizgede, bu dizgedeki herhangi iki denklem birlirleriyle tutarlı olmalarıyla beraber, denklemlerin tutarsız olmaları mümkündür. Örneğin şu denklemler tutarsızdır:
Birinci ile ikinci denklemin birbiriyle toplamaları ile
elde edilir ve bu üçüncü denkelmeden çıkartılırsa sonuç
0 = 1
olur. Dikkat edilirse bu denklemlerden herhangi bir iki denklemli dizgenin bir ortak çözümü vardır. Aynı olgu her türlü sayıda denkelemler dizgesinde de oluşabilir.
Genel bir sonuç olarak, eğer bir doğrusal denklemler dizgesindeki denklemlerin sol tarafındaki ifadeler doğrusal olarak bağımlı olursa ve sabit terimler bağımlılık bağlantısını tatmin etmiyorlarsa, tutarsızlık ortaya çıkar. Eğer bir doğrusal denklemler dizgesinin sol tarafındaki ifadeler doğrusal olarak bağımsızlarsa, bu dizge her zaman tutarlı olur.
Denklik[değiştir | kaynağı değiştir]
Aynı değişkenleri kullanan iki değişik doğrusal denklemler dizgesinin birbirleriye denk olması için ikinci dizgede bulunan denklemlerin her birinin, birinci dizgede bulunan denklemlerden cebir kullanılarak hesaplanıp elde edilebilmesi gerekir ve bunun aksinin de doğru olması gereklidir. Birbirine denk dizgeler değişken değerleri hakkında birbirine tıpatıp aynı bilgileri vermektedirler. Özellikle, eğer iki dizgenin tıpatıp aynı çözüm kümesi bulunuyorsa iki doğrusal denklemler dizgesi birbirlerine denktirler.
Doğrusal denklemler dizgesinin çözümü[değiştir | kaynağı değiştir]
Bir doğrusal denklem dizgesini çözümlemek için birkaç değişik denklem çözümleme algoritması bulunur.
Çözümü tanımlama[değiştir | kaynağı değiştir]
Eğer çözüm kümesi sonsuz değilse, genellikle bu küme olarak ve küme notasyonu kullanarak ifade edilir. Örneğin 2, 3, 4 olan çözüm kümesi olarak yazılır.
Eğer sonsuz sayıda çözüm bulunuyorsa bunu küme olarak ve küme notasyonu kullanarak ifade etmek çok güç olur. Tipik olarak değişkenlerden bazıları bağımsız (veya özgür veya parametre) olarak kabul edilirler ve herhangi bir değer alabilirler. Geride kalan değişkenler bağımsız değişkenlerin değerlerine bağlı olurlar.
Örneğin şu dizgeye ele alalım:
Bu dizge için çözüm kümesi şu denklemeler ile ifade edilebilir:
Burada bağımsız değişkendir; ve değişkenleri ye bağlıdırlar. Çözüm kümesinde bulunan herhangi nokta önce için herhangi bir değer seçmekle ve sonra da ve için bu seçilen değere tekabül eden değerleri hesaplama şeklinde ortaya çıkartılır.
Her bir bağımsız değişken çözüm kümesine bir serbestlik derecesi verir ve serbestlik derecesi sayısı çözüm kümesinin boyutuna eşittir. Örneğin, yukarıda verilen denklemin çözüm kümesi bir doğru olur; çünkü çözüm kümesi üzerinde bulunan tek bir nokta parametre değişkenin değerini şahsi seçime bağlı olarak belirlemek suretiyle ortaya çıkartılır. Daha yüksek düzenli sonsuz sayıda çözüm bir düzlemi veya yüksek boyutlu hiperdüzlemi tanımlayabilir.
Bağımsız değişkenler için değişik seçim değerleri, aynı çözüm kümesinin değişik tanımlarını oratay çıkarabilir. Örneğin yukarıda verilen denklemlerin çözümü alternatif olarak şöyle değişik şekilde tanımlanabilir:
Burada bağımsız değişken ve ve bağlı değişkenlerdir.
Değişkenlerin arka arkaya eliminasyonu[değiştir | kaynağı değiştir]
Bir doğrusal denklemler dizgesine çözüm kümesi bulmak için en basit yöntem değişkenlerin tekere teker arkaarkaya elimine edilmesidir. Bu çözüm yöntemi şöyle tanımlanabilir:
- Birinci denklemdeki tek bir değişkeni (eşit işaretinin solunda) diğer değişkenler ve sabitle (sağda) ifade edilmesini sağlayınız.
- Bu değişken için birinci denkelmeden bulunan ifadeyi dizgenin diğer denklemelerinde bulunan ifadeleri içindeki o değişken yerine konulur ve böylece yeni bir denklemler dizgesi bulunur ve bu dizgede bir önce dizgeden bir değişken eksik olur.
- Bu yeni dizgeye aynı yöntemi uygulayınız, Böylece tekrar bir değişken eksik yeni bir dizge bulunuz.
- Bu yöntemi arkaarkaya uygulayınız ve son bulunan dizge tek bir doğrusal denklem olana kadar bir yöntemi uygulamaya devam ediniz.
- Bu son tek değişkenli denklemi çözünüz ve bu son değişkenin çözüm değerini bulunuz.
- Bu değeri diğer bir öneceki dizgede geriye koyup bir diğer değişkenin çözüm değerini bulun. Bu geriye koyup çözmeyi tüm değişkenler için çözüm bulana kadar tekrarlayınız.
Örneğin şu 3 değişkenli (x, y ve z) doğrusal denklemeler dizgesini ele alalım :
Birinci deklemi x için çözelim ve şu ifadeyi elde ederiz;
x = 5 + 2z − 3y
Bu x için ifadeyi ikinci ve üçüncü doğrusal denkleme koyup bunları basitleştirelim ve şu iki değişkenli (y ve z) iki denklem bulunuruz:
Bu yeni iki değişkenli iki denklemli dizgenin birinci denklemini y için çözelim ve şu ifadeyi elde ederiz
y = 2 + 3z,
Bunu yeni dizgedeki ikinci denkleme koyalım. y için çözünce şu ifade elde edilir:
y = 2 + 3z
Bunu ikinci denkleme y için koyarsak
z = 2
ifadesini elde ederiz. Şimdi sadece z ifadeli tek doğrusal denklem dizge elimizde kalmıştır ve bu da z için şu çözümü verir:
z = 2
Arkaarkaya tek değişken eliminasyonu ile sonuçlar bulmuştuk:
Şimdi z = 2 çözümünü ikinci denkelem koyarsak y çözümü olarak
y = 8
elde ederiz; ve z = 2 ile y = 8 çözümlerini birinci denkleme koyarsak
x = −15
olarak x çözümü bulunur.
Böylece, çözüm kümesi olarak tek bir nokta olan (x, y, z) = (−15, 8, 2) elde edilmiş olmaktadır.
Sıra azaltma[değiştir | kaynağı değiştir]
a_ij katsayıları rasyonel sayılar, gercek sayılar ya da karmasik sayılar ya da herhangi bir cisimden gelen sayılar olmak üzere
a_11 x_1 + a_12 x_2 + ... + a_1n x_n = b_1
a_m1 x_1 + a_m2 x_2 + ... + a_mn x_n = b_m denklem sistemi,
A m satir ve n sutundan olusan ve değerlerini (bir cisimden alan) bir matris, x n satirlik bir sutun vektoru, b (değerlerini ayni cisimden alan) m satirlik bir sutun vektoru olmak üzere
Ax = b
seklinde yazabiliriz.
Boyle bir sistemin çözümü, x_i degiskenlerinin hangi degerlerinin denklem sistemini sağladığını bulmak anlamina gelmektedir.
Gauss tipi indirgemede temel indirgeme islemleri uygulanir.
Temel satir indirgeme islemleri aşağıdakilerdir. Dikkat edelim ki bu islemler denklem sisteminin çözüm kumesini degistirmezler.
Satir Ekleme i. satirin herhangi k katini j. satira eklemek. Bu islemi k * Satir_i + Satir_j -> Satir_j, ya da Satir (k*i+j->j) ile gösterelim.
Not: bu islem A matrisini, I+ kE_ji matrisi ile soldan carpmaya karsilik gelmektedir. Burada I kosegen terimleri 1 olan m * m boyutundaki matrisi, E_ji, sadece j. satir ve i. sutundaki terimi 1 olan matrisi göstermektedir. Boylece incelenen doğrusal sistem Ax = b yerine (I+kE_ji)A x = (I+kE_ji)b doğrusal sistemi olmaktadır.
Satir Degistirme i. satirla j. satiri yer degistirmek. Bu islemi Degistir (i,j) ile gösterelim.
Bu islem i ve j indeksleri haric diğer indekslerde sadece kosegen terimleri 1, diğer durumlarda (i,j) ve (j,i) terimleri 1 olan matris ile A matrisini soldan carpmak ile elde edilir. Boylece incelenen doğrusal sistem Ax = b yerine (I-E_ii-E_jj+E_ij+E_ji)A x = (I-E_ii-E_jj+E_ij+E_ji)b doğrusal sistemi olmaktadır.
Gauss-Jordan Indirgeme yöntemi:
Serbest degisken kavrami: Eger ilk sutun (ya da herhangi bir j. sutun) sadece sifirlardan olusuyorsa o zaman ilk degisken (ya da j. degisken) aslında denklem sistemi tarafından kısıtlanmamaktadır. Yani bu degiskenin herhangi bir degeri alabilir. Herhangi degeri alabilen degiskenlere serbest degisken denir.
Sifir olmayan ilk sutundan baslamak üzere (bu sutun j_1. sutun olsun) 1. j_1. sutundaki ilk sifirdan farklı sayınn bulunduğu satiri (bu satir i_1. satir olsun) ilk satirla degistir. Bu adimdan sonra olusan matrisin 1. satir ve j1. sutunundaki sifirdan farklı sayı A olsun. (Matristeki bu tip terimlere pivot ya da eksen terimleri denir. Cozumler bu Ikinci satirdan baslamak üzere j1. sutunda sifir olmayan ilk terim B olsun ve bu terim i_2. satirda yer alsin. 2. Ilk satirin (-B/A) katini i_2. satira ekle. Boylece i_2. satirin j_1. terimi sifira donusecektir. 3. Bu islemi bitirdikten sonra j_1. sutunda hala incelenmemis satir varken bir sonraki satira gecerek 2. adimi tekrarla. 4. j_1. sutundaki islem bittikten sonra yukaridaki adımları degistirilmis A matrisinin j1 den büyük sutunları ve 1den büyük satırlarından olusan matrise uygula. (Bundan sonraki adimda A matrisi yerine A >= j1, >=1 matrisine uygula.)
Bu işlemlerin sonunda (j_1,1) (j_2,2) (j_k,k) pivot konumları olsun. En son sifirdan farklı satirdan baslayip yukari cikarak doğrusal sistemin çözümune ulasabiliriz. Islemleri kolaylastirmak için j_v. sutunda v degerinden kucuk satirlardaki sifirdan farklı terimleri yukaridaki 2. adimdaki islemi kullanarak indirgeyebiliriz. Ayrica pivot degerlerin 1 olmasi kosulunu da ekleyerek, bu çözüm yöntemine degisiklikler yapabiliriz.
Cramer kuralı[değiştir | kaynağı değiştir]
Bu kural 1750'de "Introduction à l'analyse des lignes courbes algébriques (Cebirsel eğrilerinin analizine giriş)" adlı eserinde bu teoremi açıklayan Gabriel Cramer (1704–1752) anısına isimlendirilmiştir.
Cramer kuralı aynı sayıda değişken ile denklem bulunan doğrusal denklem dizgesinin çözüm kümesini bulmak için kullanılabilen bir ifade ortaya çıkaran bir doğrusal cebir teoremidir. Bu teorem kullanılarak çözüm tek ve tek bir çözüm kümesi bulunan doğrusal denklem dizgesi için geçerlidir. Bu halde her bir değişken için çözüm iki kare determinantın oranı olarak verilir; bu oranda pay katsayılar matrisinden o değişkene karşıt sütununun, denklemin sağ-tarafında olan sabitler vektörü ile ikame edilmesiyle elde edilen kare matrisin determinantı ve payda ise katsayılar kare matrisi determinantıdır.
Genel olarak açıklamak için aynı sayıda (n) değişkenli ve denklemli bir doğrusal denklemler dizgesinin şu matris ifadesini ele alalım:
|
|
Burada matrisi (nxn) seviyeli sonsuz değeri olmayan bir determinanti bulunan bir "katsayılar (kare) matrisi";
(nx1) seviyeli bir "degiskenler (sutun) vektoru"; ve
ise (nx1) seviyeli bir "sabitler (sutun) vektoru" olur.
değişkeni çözümü için Cramer Teoremi şöyle ifade edilir:
Burada matrisi kare matrisinin i'inci sütununun yerine sütun matrisinin konulmuş olduğu matrisdir.
İki değişkenli iki doğrusal denklemli dizge örneği[değiştir | kaynağı değiştir]
Bu örnekte, determinantların içinde hangi elemanlar bulunduğunun hemen anlaşılması içcin, katsayılar "mavi" renkli; bilinmeyenler "siyah" renkli ve katsayılar "yeşil" renkli yazılmıştır.
Üç değişkenli üç doğrusal denklemli dizge örneği[değiştir | kaynağı değiştir]
Diğer yöntemler[değiştir | kaynağı değiştir]
Homojen dizgeler[değiştir | kaynağı değiştir]
Tanımlama[değiştir | kaynağı değiştir]
Bir doğrusal denklemler dizgesinde sabitlerin hepsi 0 iselr, bu doğrsusal denklemler dizgesi homojen dizge olarak tanımlanır:
Matris ifadesiyle bir genel homojen dizge şöyle ifade edilir:
Burada
A: (mxn) düzenli katsayılar matrisi;
x: (n)-sıralı değişkenler vektörü veya sütun-matrisi ve ;
0: (m)-siralı sıfır vektör veya 0 girdili sütun-matris ;
olur.
Çözüm kümesi[değiştir | kaynağı değiştir]
Her homojen dizgenin en aşağı bir tane çözümü vardır; bu her değişkenin 0'a eşit olduğu çözüm kümesidir. Bu çözüme sıfır çözümü veya önemsiz (trivial) çözüm adı verilir.
Homoojen dizgelerin önemli olan şu diğer nitelikleri de bulunur:
- Eğer u ve v homojen dizgenin iki çözüm vektörü iseler;
vektörler toplamı da homojen dizgenin bir çözümü olur.
- Eğer u bir homojen dizgenin bir çözümünü ifade etmekte ise ve z herhangi bir skaler değer ise; o zaman
vektör çarpımı da homojen dizgenin bir çözümüdür.
Bu çözüm kümesi nitelikleri, R<sup>n</sup> nin bir Euclid-tipi altuzayı için gerekli nitelikler ile tıpatıp aynıdır. Özellikle, bir homojen dizgenin çözüm kümesi buna tekabül eden A matrisinin sıfır uzayı ile aynıdır.
Homojen olmayan dizgelerle ilişkiler[değiştir | kaynağı değiştir]
Kaynakça[değiştir | kaynağı değiştir]
- İngilizce Wikipedia "System of linear equations" maddesi 5 Mart 2011 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce)
Ayrıca bakınız[değiştir | kaynağı değiştir]
Dış bağlantılar[değiştir | kaynağı değiştir]
- İTÜ Ninova Açık Ders Malzemeleri[ölü/kırık bağlantı], Doğrusal cebir