Genel görelilik

Genel görelilik teorisi (kısaca genel görelilik), 1915'te Albert Einstein tarafından yayımlanan, kütleçekimin geometrik teorisidir ve modern fizikte kütle çekiminin güncel açıklamasıdır.[1] Genel görelilik, özel göreliliği ve Newton'un evrensel çekim yasasını genelleştirerek, yerçekimin uzay ve zamanın veya dört boyutlu uzayzamanın geometrik bir özelliği olarak birleşik bir tanımını sağlar. Özellikle uzayzaman eğriliğine maruz kalmış maddenin ve radyasyonun, enerjisi ve momentumuyla doğrudan ilişkilidir. Bu ilişki, kısmi bir diferansiyel denklemler sistemi olan Einstein alan denklemleriyle belirlenir.
Genel göreliliğin zamanın akışı, uzayın geometrisi, serbest düşme yapan cisimlerin hareketi, ışığın yayılımı gibi konulardaki öngörüleri, klasik fiziğin önermeleri ile belirgin farklılıklar gösterir. Kütleçekimsel zaman genişlemesi, kütleçekimsel merceklenme, ışığın kütleçekimsel kızıla kayması, kütleçekimsel zaman gecikmesi bu farklılıkların örnekleridir. Genel göreliliğin bugüne kadarki tüm önermeleri deney ve gözlemler ile doğrulanmıştır. Her ne kadar genel görelilik kütleçekimin tek göreli kuramı olmasa da, deneysel veri ile uyum sağlayan en basit teoridir. Buna rağmen, teorinin hala cevaplayamadığı sorular varlığını sürdürmektedir. Bunlara örnek olarak pioneer anomalisi, galaksilerin dönüş eğrisi ve genel görelilik ile kuantum mekaniğinin yasalarının hangi şekilde bağdaştırılarak, tamamlanmış kendi içinde tutarlı bir kuantum alan kuramı yaratılabileceğidir.
Einstein'ın teorisinin astrofiziğe kayda değer etkileri olmuştur; örneğin, büyük bir yıldızın ömrünün sonuna yaklaştığı bir zamanda içine çökerek karadelik oluşturduğuna işaret eder. Bazı astronomik cisimlerin yaydığı yoğun radyasyona karadeliklerin sebep olduğuna dair yeterli kanıt mevcuttur. Örneğin mikrokuasarlar, yıldız kaynaklı kara delikler ve etkin galaksi çekirdekleri, süper kütleli kara deliklerin varlıklarının bir sonucu olarak oluşurlar. Işığın kütleçekim nedeniyle bükülmesi, uzaktaki bir astronomik cismin gökyüzünde aynı anda birden fazla yerde görüntüsünün belirmesine sebep olan, kütleçekimsel merceklenme olarak adlandırılan bir duruma neden olur. Genel görelilik aynı zamanda, bugüne kadar ancak dolaylı olarak gözlenmiş olan, kütleçekim dalgalarının da varlığını öngörmektedir. Buna dair doğrudan gözlemlerin yapılması LIGO ve NASA/ESA Laser Interferometer Space Antenna (Lazer girişimölçer uzay anteni) gibi projelerin amaçlarıdır. Tüm bunlara ek olarak genel görelilik, evrenin durmaksızın genişleyen modelinin bugünkü kozmolojik modelinin temelidir.
Tarihi[değiştir | kaynağı değiştir]
1905'te özel görelilik teorisini açıkladıktan hemen sonra, Einstein bu göreli çerçeveye kütleçekimini nasıl dahil edeceğine dair fikir yürütmeye başladı. 1907 yılında serbest düşen bir gözlemciyi ele alan basit bir düşünce deneyinden yola çıkarak, kütleçekimin göreli teorisi üzerine sekiz yıl sürecek bir araştırmaya başladı. Birçok denemenin ardından, bugün Einstein alan denklemleri olarak bilinen çalışmasını sonlandırarak, Kasım 1915'te Prusya Bilimler Akademisi'nde sundu. Bu denklemler Einstein'ın kuramının çekirdeğini oluşturur ve herhangi bir maddenin uzay ve zamanı nasıl etkilediğini belirler.[2]
Einstein alan denklemleri doğrusal olmayan ve çözümü oldukça zor olan diferansiyel denklemlerdir. Einstein, başlangıçta kuramını öngörüye dayanarak biçimlendirmişti. Ancak çok zaman geçmeden 1916 yılında, astrofizikçi Karl Schwarzschild Einstein alan denklemlerinin ilk kesin ve sıfırdan farklı çözümünü bulmayı başardı. Bu çözüm Schwarzschild metriği olarak adlandırılır.
Schwarzschild metriği ile, kütleçekimsel içe çökmenin son evrelerinin, yani bugün bilinen adıyla karadeliklerin tanımının temelleri ortaya koyulmuştur. Aynı yıl Schwarzschild çözümünün elektrik yüklü cisimler için genelleştirilmiş çözümü olan Reissner–Nordström çözümüne ulaşıldı. Bugün bu çözüm elektrik yüklü karadelikler için kullanılmaktadır.[3]
1917'de Einstein, kuramını, evrenin bütününe uygular ve göreli kozmolojinin temelini atar. Genel göreliliğin öngörüsü evrenin genişlemekte ya da büzülmekte olduğu iken, Einstein evrenin durağan olduğunu düşünmüştür ve bunu sağlamak için orijinal alan denklemlerine kozmolojik sabit olarak adlandırdığı yeni bir değişken ekler.[4]
Ancak 1929'da Hubble, evrenin durağan olmadığını, uzak gökadaların tayfının kırmızıya kaydığını buldu. Friedmann 1922'de yaptığı çalışmada genişleyen evren modelini kozmolojik sabit kullanmaksızın ortaya koymuştur. Lemaître bu çözümü Büyük patlama'nın ilk modelini formüle etmek için kullanmıştır.[5] Evrenin genişlediğine dair gözlemlerden sonra Einstein, kozmolojik sabiti, "hayatının en büyük hatası" olarak tanımlar.[6]
Bu süre zarfında genel görelilik merak uyandıran bir kuram olarak kalır. Özel göreliliğin yasaları ile uyumlu olması ve Newton kuramının açıklayamadığı bazı etkilere cevap getirmesi nedeniyle açıkça Newtonsal kütleçekime karşı bir üstünlüğü vardır. 1915'te kuramının Merkür'ün günberi devinimi sorununa isteğe bağlı değişkenler kullanmadan nasıl açıklık getirdiğini, Einstein bizzat kendisi açıklamıştır.[7] 1919'da Eddington tarafından yönetilen bir keşif, 29 Mayıs 1919 tarihindeki tam güneş tutulması sırasında yıldız ışığının güneş tarafından aynı genel göreliliğin öngördüğü şekilde büküldüğünü doğrulamış[8] ve bu, Einstein'ın ününü daha da arttırmıştır.[9] Ancak kuram, altın çağını 1960 ve 1975 yılları arasında yaşamış ve ancak bundan sonra teorik fiziğin ana dallarından biri olarak kabul görmüştür.[10]
Klasik mekanikten genel göreliliğe[değiştir | kaynağı değiştir]
Genel göreliliği iyi anlamanın yolu klasik mekanik ile benzerliklerini ve farklılıklarını gözden geçirmektir. Öncelikle klasik mekaniğin ve Newton'un kütleçekim yasasının geometrik bir şekilde tanımlanabileceği bilinmelidir. Bu tanım özel göreliliğin yasaları ile birleştirilerek, genel göreliliğin yasaları becerikli bir fizikçi tarafından türetilebilir.[11]
Newton kütleçekiminin geometrisi[değiştir | kaynağı değiştir]

Klasik mekaniğin özünde, bir cismin hareketinin serbest (ya da ivmeli) hareketinin ve bu serbest hareketten sapmaların bileşimi yatar. Bu sapmalar cisme etkiyen dış kuvvetlerin varlığından kaynaklanır ve kuvvetin tanımı Newton'un ikinci yasası ile verilmiştir. İkinci yasa bir cisme etkiyen net kuvvetin cismin eylemsiz kütlesi ve ivmesinin çarpımı kadar olacağını söyler.[12] Cismin tercih edeceği eylemsiz hareket, uzay ve zamanın geometrisine bağlıdır: Standart olarak klasik mekaniğin konuşlanma sistemlerinde serbest hareket yapan cisimler düz çizgiler boyunca sabit hızla hareket ederler. Günümüz terminolojisinde, cisimlerin eğri uzayzamandaki bu yollarına jeodezik denilmektedir.[13] Aksine bir zaman koordinatının yanı sıra, gözlemleyerek ve dış kuvvetleri (elektromanyetizma ve sürtünme gibi) tolerans ederek tanımlanan eylemsiz hareketlerin uzayın geometrisini belirlemek için kullanılması beklenilebilir. Fakat yerçekimi devreye girer girmez bir belirsizlik oluşur. Newton'un evrensel kütleçekim yasası ve bağımsız doğrulanan Eötvös deneyi ve onun ardıllarına göre, serbest düşüşün bir evrenselliği vardır. (ayrıca eylemsiz ve pasif yerçekimsel kütlenin evrensel eşitliği ya da zayıf eşdeğerlik ilkesi olarak da bilinir): serbest düşüş halindeki test cisminin yörüngesi sadece pozisyonuna ve ilk hızına bağlıdır fakat materyal özelliklerine bağlı değildir. Bunun basitleştirilmiş versiyonu Einstein’ın asansör deneyinde, sağ tarafta gösterilen figürde, somutlaştırılır. Küçük kapalı bir odadaki bir gözlemci için odanın kütleçekimsel alanda durağan ya da kütleçekimine eşit kuvvet üreten ve ivmelenen bir rokette boş uzayda olup olmadığına aşağı bırakılan bir cisim gibi yörüngelerini haritalayarak karar vermek mümkün değildir.
Serbest düşüşün evrenselliği göz önünde tutulursa eylemsiz hareket ile kütleçekimsel kuvvet etki altındaki hareket arasında gözlemlenilebilir fark yoktur. Bu kütleçekimi etkisi altında serbest düşüş yapan cisimler olarak adlandırılan eylemsiz hareketin yeni bir sınıfının tanımını destekler. Tercih edilmiş hareketlerin yeni sınıfı ayrıca matematik terimleri ile uzayın ve zamanın geometrisini açıklar.Bu bir kütleçekimsel potansiyelin değişim derecesine bağlı olan özel bağlantı ile ilişkili jeodezik bir harekettir. Bu yapıdaki uzay hala tipik bir Öklit geometrisine sahiptir. Fakat uzay zaman bir bütün olarak daha karışıktır. Farklı test parçacıklarının serbest düşüş yörüngelerini takip eden basit bir düşünce deneyi kullanarak gösterilebileceği üzere, bir parçacığın hızını gösterebilen uzay zaman vektörlerinin (zaman vektörleri gibi) taşınmasının sonucu parçacığın yörüngesine göre değişiklik gösterecektir; matematiksel konuşmak gerekirse Newtonsal ilişkisi tümlevlenemez. Bundan uzay zamanın eğri olduğu sonucu çıkarılabilir. Sonuç sadece eşdeğişken (kovaryant) kavramları kullanan Newton kütleçekiminin geometrik bir denklemlendirilmesidir, yani herhangi bir koordinat sisteminde geçerli olan bir tanımdır. Bu geometrik tanımda gelgit etkileri (serbest düşüş halindeki cisimlerin göreceli ivmesi) kütlenin varlığının geometriyi nasıl değiştirdiğini gösteren bağlantının türevi ile ilişkilidir.
Göreli Genelleme[değiştir | kaynağı değiştir]
Geometrik Newton yerçekimi ne kadar ilgi çekici olsa da temeli olan klasik mekanik, sadece (özel) göreli mekaniğin sınırlayıcı bir durumudur. Kütleçekiminin ihmal edilebileceği simetri dilinde klasik mekanikteki fizik Galile değişmezliği yerine genel görelilikte olduğu gibi Lorentz sabitidir. (Genel göreliliği tanımlayan simetri ayrıca öteleme ve dönmeyi içeren Poincaré grubudur). İkisi arasındaki farklılık ışık hızına yaklaşan hızlarda ve yüksek-enerji durumlarında uğraştığımızda daha fazla öneme sahip olur.
Lorentz simetrisi ile ilave yapılar devreye girer. Bunlar ışık konileri grubu (sol taraftaki resim) ile tanımlanırlar. Işık konileri nedensel bir yapı oluştururlar: her A olayı için prensipte ya etkileyen ya da sinyal yolu ile ya da ışıktan fazla hızlı yol almasına gerek olmayan etkileşimlerden (resimdeki B olayında olduğu gibi) etkilenen olaylar topluluğu vardır ve böyle bir etki için olaylar topluluğu mümkün değildir. (resimdeki C olayında olduğu gibi) Bu gruplar gözlemciden bağımsızdır. Serbest düşüş yapan parçacıkların hayat çizgisi ile bağlantılı olarak ışık konileri uzay zamanın yarı Riemannian metriğini tekrar oluşturması için kullanılabilir, en azından pozitif bir sayısal faktöre bağlı olarak. Matematik terimlerinde bir konform yapıyı tanımlar.
Özel görelilik kütleçekimi yokluğunda tanımlanır. Bu yüzden pratik uygulamalar için ne zaman kütleçekimi ihmal edilebilirse edilsin bu uygun bir modeldir. Eğer yerçekimini dahil eder ve serbest düşüsün evrenselliğini varsayarsak bir önceki bölümdeki benzer bir düşünce uygulanır: evrensel eylemsiz çerçeveler yoktur. Bunun yerine serbest düşüş yapan parçacıkların yanı sıra hareket eden yaklaşık olarak eylemsiz çerçeveler vardır. Uzay-zaman diline çevrilirse, kütleçekimi serbest bir eylemsiz çerçevesi tanımlayan düz zaman çizgileri birbirine göre eğilmiş çizgilere dönüşür (kütleçekiminin dahil edilmesinin uzay zaman geometrisinde bir değişiklik gerektirdiğini farz edersek).
Serbest düşüşteki yeni kısmi çerçevelerin özel görelilik yasalarının (teori ışığın yayılımına dayalıdır ve bu yüzden elektromanyetizmaya da bağlıdır) uygulandığı referans çerçeveleri ile uyuşup uyuşmadığı açık değil. Fakat özel göreli çerçeveler hakkında farklı varsayımlar kullanarak (dünyada sabit olmaları ya da serbest düşüşte olmaları gibi) kütleçekimsel kırmızıya kayma tahminleri türetilebilir. Kütleçekiminden dolayı kırmızıya kayma ışığın yerçekimsel bir alana doğru yayılırken frekansının değişmesidir. Gerçek ölçümler serbest düşüş çerçevelerinde ışığın özel görelilikte olduğu gibi yayıldığını gösterir. Serbest düşüş (ve dönmeyen) çerçeve referanslarındaki özel görelilik yasası ile adlandırılan durumun genelleştirilmesi Einstein'in eşitlik ilkesi olarak bilinir. (özel-göreli fiziği kütleçekimini içerecek şekilde genelleştirmek için çok önemli yol gösterici bir ilkedir.)
Aynı deneysel bilgiler yerçekimsel bir alanda saatlerle ölçülen zaman özel görelilik kurallarını takip etmez. Uzay zaman geometrisi dilinde Minkowski metriği ile ölçülmez. Newtonsal durumda olduğu gibi bu daha fazla genel bir geometriyi akıla getirir. Küçük ölçeklerde serbest düşüşteki bütün çerçeve referansları eşittir ve yaklaşık olarak Minkowakiandır. Bu yüzden Minkowski uzayının eğri bir genelleştirilmesi ile uğraşmıyoruz. Geometriyi özellikle açıların ve uzunlukların nasıl ölçüldüğünü tanımlayan metrik tensörü özel göreliliğin Minkowski metriği değildir. Yarı-Riemann metriği olarak bilinen bir genellemedir. Hatta her Reimannian metriği doğal olarak özel bir bağlantı türü ile ilişkilidir, Levi-Civita bağlantısı ve aslında eşitlik ilkesini karşılayan ve uzayı Minkowskian yapan bir bağlantıdır. (uygun yerel bir eylemsiz koordinatlarda metrik Minkowskiandır ve kısmi türevleri ve bağlantı katsayıları sıfır olur.)
Einstein'in Denklemleri[değiştir | kaynağı değiştir]
Kütleçekiminin göreli geometrik versiyonunun etkilerini formülleştirdikten sonra yerçekiminin kaynağı sorusu geride kalır. Newton yerçekiminde kaynağı kütledir. Özel görelilikte kütle stresin(basınç ve kayma) yanı sıra enerji ve moment yoğunlukları içeren enerji-momentum tensör olarak adrandırılan daha genel bir niteliği çağrıştırır. Eşitlik ilkesini kullanarak bu tensör kolayca eğri uzay zamana genelleştirilir. Analojiyi geometrik Newton yerçekimi ile kaleme alırsak yerçekimi için alan denkleminin bu tensör ve özel bir gelgit etkilerinin sınıfını tanımlayan Ricci tensörü ile ilgili olduğunu varsaymak doğaldır (ilk başta durağan ve sonra serbest düşüş yapan küçük bir test parçacıkları grubu için hacimdeki değişim). Özel görelilikte enerjinin korunumu (momentum, enerji durumuna karşılık gelir) momentum tensörü ıraksayışı serbesttir. Bu formül ayrıca kısmi türevleri diferansiyel geometride çalışılan eşdeğişkin türevleri olan eğri-manifold karşılıkları ile değiştirerek kolayca eğri uzaya genelleştirilebilir. Bu ek koşul ile enerji-moment tensörünün eğdeğişken ıraksayışı ve bu nedenle denklemin diğer tarafında ne olursa olsun Einstein’in (alan) denklemleri olarak adlandırılan en basit bir takım denklemler:
Einstein'in alan denklemleri
Sol taraftaki Einstein tensörüdür, Ricci tensörünün özel ıraksayışı serbest kombinasyonu ve metriğidir. simetriktir. Özellikle,
eğrilik skalerdir. Ricci tensörü daha genel Riemann eğrilik tensörü ile ilgilidir.
Sağ taraftaki, enerji-moment tensörüdür. Bütün tensörler soyut dizin semboller ile yazılır. Gezegen yörüngeleri için teorinin tahminleriyle gözlemlenen sonuçları eşleştirirsek orantı sabiti olarak sabitlenebilir, kütle çekimi sabiti ve ışığın hızıdır. Enerji-momentum tensörünün ortadan kalkması için madde mevcut olmadığında, sonuçlar vakum Einstein denklemleridir,
Tanım ve temel uygulamalar[değiştir | kaynağı değiştir]
Bir önceki bölümde bahsedilen türev, inşa modeli için nasıl bir teori kullanılabileceğini açıklayan, fizikteki önemli bir sorunun adresi ve anahtar özelliklerini tanımlayan, genel göreliliği tanımlayabilmek için gerek duyulan bütün bilgileri içerir.
Tanım ve temel özellikler[değiştir | kaynağı değiştir]
Genel görelilik yerçekiminin bir metrik teorisidir. Dört boyutlu bir geometri, uzay zamanı belirten pseduo-Reimannian, ile uzay zamanda bulunan enerji-moment arasındaki ilişkiyi tanımlayan Einstein’in denklemleri bir çekirdek gibidir. Kütleçekimi kuvveti (serbest düşüş, orbital hareket ve uzay aracı yörüngeleri gibi) etkisini isnat eden klasik mekanikteki olay, genel görelilikteki uzay zamanın eğik geometrisindeki eylemsiz harekete denk gelir. (nesneleri düz ve doğal yollarından saptıran bir kütleçekimi kuvveti yoktur.) Aslında kütleçekimi uzay ve zamandaki değişikliklerine karşılık gelir- nesnenin doğal bir biçimde takip edebileceği mümkün en düz yolları değiştirir. O halde eğiklik maddenin enerji- momentumundan dolayı oluşur. John rölativist Archibald Wheeler’ e göre uzay zaman maddeye nasıl hareket edeceğini söyler, madde uzaya nasıl bükeceğini söyler.
Genel görelilik, klasik fiziğin skaler kütleçekimi potansiyelini simetrik bir iki-kademeli tensör ile değiştirirken, ikincisi bazı sınırlayıcı durumlarda birincisine indirgenir. zayıf kütleçekimi alanları ve ışığın hızına göre yavaş hız için teorinin tahminleri Newton’un evrensel kütleçekimi yasasını birleştirir.
Tensörleri kullanarak oluşturulduğu üzere, genel görelilik genel kovaryansı gösterir. Yasaları (ve genel göreli çerçeve içinde formüle edilen diğer yasalar) tüm koordinat sistemlerinde aynı biçimi alır. Ayrıca, teori herhangi bir değişmez geometrik arka plan yapısı içermez, yani arka plandan bağımsızdır. Böylece göreliliğin daha katı bir genel ilkesini, yani fizik yasalarının tüm gözlemciler için aynı olduğu ilkesini karşılar. Yerel olarak, eşdeğerlik ilkesinde ifade edildiği gibi, uzay-zaman Minkowskiyen'dir ve fizik yasaları yerel Lorentz değişmezliği sergiler.
Model oluşturma[değiştir | kaynağı değiştir]
Genel göreli model oluşturmanın ana fikri Einstein’in denklemlerinin bir çözümünden gelir. Einstein’in denklemleri ve maddenin özellikleri için uygun denklemlere göre böyle bir çözüm spesifik bie yarı-Riemmannian kopyası (genellikle spesifik koordinatlarda metrik vererek tanımlanan) ve spesifik o kopyada tanımlanan madde alanlarından oluşur. Madde ve enerji Einstein’in denklemlerini sağlamalıdır, bu yüzden özellikle maddenin enerji-moment tensörü ıraksaması sabit olmalıdır. Tabii ki madde ayrıca herhangi ek denklemleri de sağlamalıdır. Kısacası, böyle bir çözüm genel göreliliğin yasalarını tatmin eden bir modeldir ve mümkün olduğunca herhangi maddeyi ele alan ilave yasalar ortaya konulabilir.
Einstein’in denklemleri doğrusal olmayan kısmi diferansiyel denklemlerdir ve çözümü de zordur. Yine de, sadece birkaçı direkt fiziksel uygulamalara sahip olsa da, birkaç tamı tamına doğru çözümleri vardır. Bilinen en iyi tam çözümleri ve ayrıca fizik görüşü açısından en ilgi çekici olanları Schwarzschild çözümü, Reissner-Nordström çözümü ve Kerr metriği (başka bir boş uzayda her biri kara cismin belirlenmiş bir türüne karşılık gelir) ve Friedmann–Lemaître–Robertson–Walker ve de Sitter evrenleridir (her biri genişleten bir kozmosu tanımlar). Büyük teorik görüşünün tamı tamına çözümleri Gödel evrenini (eğri uzay zamanlarda, zaman yolculuğunun merak uyandırıcı bir olasılığına açık), Taub-NUT çözümü (homojen fakat eşyönsüz bir evren) ve anti-de Sitter uzayını (son zamanlarda Maldacena ikiliği ile ön planda olan) içerir.
Tam çözümleri bulmadaki zorluk durumunda bilgisayarda integral ile ya da asıl çözümlerin küçük sapmalarını düşünerek Einstein’in alan denklemleri ayrıca sık sık çözülür. Numarasal göreli alanlarda, iki çarpışan kara delik gibi Einstein’in ilginç durumlarda denklemlerini çözmek için ve uzay zaman geometrisini benzeştirmek için güçlü bilgisayarlar kullanılır. Özellikle yeterli bilgisayar kaynakları ile bu metotlar herhangi bir sisteme uygulanabilir ve yalın tuhaflıklar gibi temel problemlere çözüm kazandırabilir. Doğrusallaşmış kütleçekimi ve genelleştirilmesi, post-Newton genişlemesi, gibi sapma teorileri ile yaklaşık sonuçlar bulunabilir. Işığa kıyasla yavaşça hareket eden bir madde dağılımı içeren uzay zamanın geometrisi için çözümde ikincisi sistematik bir yaklaşım sağlar. Genişleme terimlerin bir serisini içerir; ikinci terimler genel görelilik yüzünden Newton’un teorisine daha az düzeltmeleri gösterirken, birinci terimler Newton yerçekimini gösterir. Bu genişlemenin büyümesi alternatif teoriler ile genel göreliliğin tahminleri arasında nicel kıyaslamalara olanak sağlayan parametre edilmiş post-Newton’ dur.
Einstein’in teorisinin sonuçları[değiştir | kaynağı değiştir]
Genel görelilik birçok fiziksel sonuçlara sahiptir. Bazıları direkt teorinin aksiyomlarından takip eder, bazıları ise sadece Einstein’in ilk yayını olan 90 yıllık araştırmaları ile açıklığa kavuşur.
Kütleçekimsel zaman genişleşmesi ve frekans kayması[değiştir | kaynağı değiştir]
Eşdeğerlik ilkesinin geçerli olduğunu varsayarsak, zamanın akışını kütleçekimi etkiler. Kütleçekimi haznesine gönderilen ışık maviye kayar ve diğer yönden gönderilen(kütleçekimi haznesinden çıkan) ışık kızıla kayar; bu iki etkiler kütleçekimi ile frekans kayması olarak adlandırılır. Daha genel olarak, uzakta olan yerler ile karşılaştırıldığında büyük bir cismin yanında işlem daha yavaş gerçekleşir; bu etki kütleçekimsel zaman genişlemesi olarak bilinir.
Kütleçekimsel kırmızıya kayma laboratuvarda ve astronomik gözlemlerle ölçülmüştür. Küresel Konumlama Sistemi operasyonunun bir yan etkisi karşıladığı halde, dünyanın kütleçekimi alanındaki kütleçekimsel zaman genleşmesi atomik saatler kullanılarak ölçülmektedir. Bütün sonuçlar genel görelilik ile uyuşmaktadır. Fakat doğruluğun geçerli seviyesinde bu gözlemler eşiklik ilkesinin geçerli olduğu genel görelilik ve diğer teoriler arasındaki farkı ayırmaz.
Işık sapması ve kütleçekimsel zaman gecikmesi[değiştir | kaynağı değiştir]
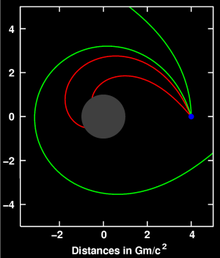
Genel görelilik, ışığın yolunun bir yıldızın yakınından geçerken uzay-zamanın eğriliğini izleyeceğini öngörür. Bu etki, yıldızların veya uzak kuasarların ışığının Güneş'ten geçerken saptığının gözlemlenmesiyle doğrulandı.
Bu ve ilgili tahminler, ışığın ışık benzeri veya boş jeodezik olarak adlandırılan şeyi takip ettiği gerçeğinden kaynaklanmaktadır (klasik fizikteki ışığın hareketine doğru olan düzgün çizgilerin bir genelleştirilmesi). Bu tür jeodezikler özel görelilikteki ışık hızı sabitinin genelleştirilmeleridir. Uygun uzay zaman modelleri (ya dış Schwarzschild çözümü ya da tek bir kütleden fazlası için Newton-sonrası açılımlar) açıklandığı üzere, yerçekiminin ışığın ortaya dağılmasındaki birçok etkileri. Serbest düşüşün evrenselliğini ışığa vererek ışığın bükülmesi türetebildiği halde, bu tür hesaplamalardan sonuçlanan ışının sapması sadece genel görelilik tarafından verilen değerin yarısıdır.
Kütleçekimsel zaman gecikmesi ışığın sapması ile yakından ilgili olduğu için kütleçekimsel bir alana doğru ışık sinyallerinin hareket etmesi alan yokluğundakilere göre daha uzun sürer.bu tahmin için çok fazla başarılı testler yapılmaktadır. parametre edilmiş post-Newtoncu biçimcilikte ışığın sapmasının ve kütleçekimsel zaman gecikmesinin ölçümleri kütleçekiminin uzayın geometrisi üzerindeki etkisini şifreleyen γ ile adlandırılan bir parametreyi belirler.
Yörüngesel etkiler ve göreliliğin yönü[değiştir | kaynağı değiştir]

Temel metin: Genel görelilikte Kepler sorunu
Yörüngesel cisimler konusundaki birçok tahminler açısından genel görelilik klasik mekanikten farklıdır. Gezegensel yörüngelerin tam bir dönüşünü tahmin eder. (kütleçekimsel dalgaların emilimi ve göreliliğin yönü ile ilgili etkilerin neden olduğu yörüngesel gecikmelerde olduğu gibi)
Apsislerin devinimi[değiştir | kaynağı değiştir]
Genel görelilikte herhangi bir yörüngenin apsisi (yörüngesel hareket eden bir cismin sistemin kütlesinin merkezine en yakın olduğu yer) devinecektir- yörünge eliptik değildir fakat odağına göre dönen bir elipse benzer(gül eğimi gibi bir şekil ile sonuçlanır (resmi gör)). Einstein ilk olarak yörüngesinde hareket eden bir cisme bir test parçacığı gibi davranarak ve Newton limitini gösteren yaklaşık bir metrik kullanarak bu sonucu çıkardı. Urbain Le Verrier tarafından 1859 da keşfedilen Merkür gezegeninin anormal günberi değişiminin açık bir açıklamasını veren teorisi onun için kütleçekimsel alan denklemlerinin doğru halini tanımladığı önemli bir kanıttı. Tam tamına Schwarzschild metriği (uzay zamanı küresel bir kütle etrafında tanımlayan) ya da daha gele post-Newton biçimciliği kullanarak etki ayrıca türetebilir. Bu durum, bir cismin kütleçekiminin öz enerjine katkısı (Einstein’in denklemlerinin doğrusal olmayışlığında şifrelenen) ve kütleçekiminin uzayın geometrisindeki etkisinden dolayıdır. Kesin devinim ölçümleri sağlayan bütün gezegenler (Merkür, Venüs ve Dünya) için göreli devinim gözlenmektedir.
Yörüngesel gecikme[değiştir | kaynağı değiştir]

Yörünge gecikmesi Genel göreliliğe göre, ikili sistem enerji kaybederken yerçekimsel dalgaları emecektir. Bu kayıp yüzünden iki yörüngesini izleyen iki cisim arasındaki mesafe azalır ve bu yüzden yörüngesel periyotları da azalır. Güneş sisteminde ya da sıradan çift yıldızlar için etki çok az gözlemlenebilir. İki yörüngesel hareket yapan nötron yıldızları (birisi pulsardır) yakın bir çift pulsar için değildir; pulsardan Dünyadaki gözlemciler, yörüngesel periyodun ölçümlerini sağlayan ve yüksek doğruluğa sahip saat gibi görev yapabilen düzenli bir radyo bakliyatlarını alabilirler. Nötron yıldızları çok yoğun olduğu için enerjinin önemli bir miktarı kütleçekimsel radyasyon olarak salınır.
Yerçekimsel dalgaların salınması yüzünden yörüngesel periyotlarındaki azalmanın ilk gözlemi 1974'te keşfedilen PSR1913+16 çift pulsarı kullanarak Hulse ve Taylor tarafından yapıldı. 1993 Nobel Ödülünü kazandıkları yerçekimsel dalgaların ortaya çıkımı bir ilkti. O zamandan beri birçok diğer pulsarlar bulundu; özellikle PSR J07337-3039 çift pulsarı.
Jeodezik devinim ve çerçeve sürüklenmesi[değiştir | kaynağı değiştir]
Birçok göreli etkiler yönün göreliliği ile direkt bağlantılıdır. Biri jeozdezik devinimdir: eğik uzay zamanda serbest düşüşteki bir jiroskobun yönünün ekseni, böyle bir jiroskop mümkün olduğunca kararlı bir biçimde bir yolu sürdürmenin yolunu gösterdiği halde uzak yıldızlardan gelen ışığın yönü ile karşılaştırıldıkça değişecektir. (paralel taşıma) Ay-Dünya sistemi için bu etki ayla ilgili lazer değişimleri yardımı ile ölçülmektedir. Daha yaygın olarak, % 0.3 den daha iyi bir hassasiyet ile Kütleçekimi B Araştırması uydusunda test kütleleri için ölçülmektedir.
Dönen bir kütlenin yanında çerçeve sürüklenmesi etkisi adında etkiler vardır. Uzak bir gözlemci kütleye yakın cisimler sürükleneceğini saptayacaktır. Bu aşırı dönen kara delikler içindir. (sıcak bir alana giren herhangi bir cisim için dönme kaçınılmazdır) Bu tür etkiler serbest düşüşte jiroskopların yönelimi üzerindeki etkileri ile tekrar test edilebilir. Az çok tartışmaya açık testler LAGEOS uyduları kullanarak yapılmaktadır. ayrıca Evrensel Mars Araştırmacısının Mars üzerine incelemesi kullanılmaktadır.
Astrofizik uygulamaları[değiştir | kaynağı değiştir]

Temel metin: Kütleçekimsel lens Kütleçekimi ile ışığın sapması astronomik olayın yeni bir sınıfının sorumludur. Eğer ağır bir cisim astronom ile uygun kütleli ve göreli mesafeli uzak hedef bir etkiler arasına yerleştirilir ise astronom hedefin birçok saptırılmış görüntülerini görecektir. Bu tür etkiler kütleçekimsel lens olarak bilinir. Görünüşe ve kütle dağılımına dayanarak iki ya da ikiden fazla görüntüleri olabilir, parlak çember Einstein’in çemberi olarak bilinir. En eski örneği 1979 yılında keşfedildi ve o zamandan beri yüz den fazla kütleçekimsel lensler gözlemlendi. Çözülebilmesi için birçok görüntüler birbirlerine yakın olsa bile etki hala ölçülebilir. (birçok mikro lens olayları gözlemlenmektedir)
Kütleçekimsel lens gözlemsel astronomide gelişmektedir. Kara deliğin varlığını ve yayılımını göstermek için kullanılır. (uzak galaksileri gözlemlemek için doğal bir teleskop sağlar ve bağımsız Hubble sabitinin tahminini elde etmeye katkıda bulunur) Lens bilgilerinin statiksel değerlendirmeleri galaksilerin yapısal evrimine değerli bir anlayış katar.
Kütleçekimsel dalga astronomisi[değiştir | kaynağı değiştir]
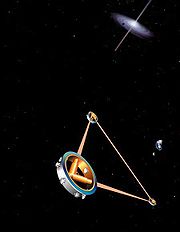
Çift pulsarların gözlemleri kütleçekimsel dalgaların varlığı için güçlü dolaylı bir kanıt sağlar. (yukarıdaki yörüngesel gecikmeyi gör) Fakat kozmosun derinliklerinden bize ulaşan kütleçekimsel dalgalar direkt olarak algılanmamıştır. Görelilikle ilgilenen araştırmacıların temel amacı böyle bir buluştur. Birçok kütleçekimsel dalga buluşları denenmektedir ve en önemlisi ferrometrik detektörlerdir: GEO 600, LIGO (iki detektör), TAMA 300 ve VIRGO . Çeşitli zamanlama okları 10−9 -10−6 Hertz frekansları aralığındaki kütleçekimsel dalgaları(çift çok ağır kara deliklerin oluşturduğu) algılamak için milisaniye pulsarları kullanır. Avrupalı uzay detektörü Elısa / NGO sürekli gelişme aşamasındadır. (başlangıcı 2015 e kadar olan haberci bir görev LISA Pathfinder ile) Kütleçekimsel dalgaların gözlemleri elektromanyetik spektrumdaki gözlemleri tamamlamaya garanti verir. Kara delikler ve nötron yıldızları, beyaz cüceler, süpernova patlamalarının türleri hakkında bilgi vermeleri beklenir.
Kara delikler ve diğer yoğun cisimler[değiştir | kaynağı değiştir]
Bir cismin kütlesinin yarıçapına oranı yeterince büyük olduğu zaman genel görelilik bir kara deliğin(hiçbir şeyin, ışığın bile kaçamadığı düşünülen) oluşumunun kaçabileceğini ileri sürer. Son zamanlarda kabul edilmiş 1.4 güneş kütleleri civarında nötron yıldızları, yıldızımsı kara delikler ve yıldız evrimi modelleri, büyük kütleli yıldızların gelişimi için final durum olduğu düşünülür. Genellikle bir galaksi merkezinde birkaç milyonluk güneş kütleye sahip bir süper kütleli kara deliğe sahiptir.

Astronomik olarak yoğun cisimlerin kütleçekimsel enerjiyi elektromanyetik radyasyona çeviren fevkalade mekaniği, onlara en önemli özelliğini katar. Gaz maddelerin ya da tozun yıldız ya da süper kütleli kara deliklere düşüşü göz alıcı bir şekilde ışıldayan bazı cisimler için sorumlu olduğu düşünülür. (oldukça galaksi ile ilgili yıldız boyutundaki cisimler(mikro yıldızımsı gökcisimleri gibi) üzerindeki aktif çekirdeğin farklı türleri) Özellikle, yığılma yaklaşık ışık hızı ile uzaya fırlatılmış yüksel enerjili parçacıkların ışınlarına odaklı göreli jetlere neden olabilir. Genel görelilik bütün bu olayları modellemede merkez bir rol oynar ve gözlemler teori ile tahmin edilen kara deliklerin varlıkları için güçlü bir kanıt sağlar. Kara delikler ayrıca kütleçekimsel dalgalar için olan araştırmalarda amaçlarında tebliğ içindedir. İkili kara deliği birleştirme Dünyadaki detektörlere ulaşan en güçlülerden bazı yerçekimsel dalga sinyallerini takip etmelidir ve birleşmeden direkt önceki safha, birleşme olaylarının mesafesini azaltmak için bir standart mum olarak kullanılabilir. Bu yüzden uzak mesafelerde kozmik genişlemenin araştırması olarak hizmet eder.
Kozmoloji[değiştir | kaynağı değiştir]

Kozmolojinin geçerli modelleri kozmoloji sabitini Λ içeren Einstein’in alan denklemelerine dayanır çünkü kozmosun büyük ölçekli dinamiğine büyük etkisi vardır.
uzay zaman metriğidir . Bu ileri denklemlerin eş yönlü ve homojen çözümleri, Friedmann-Lemaitre-Robertson-Walker çözümleri, Büyük Patlamadan daha evvel 14 milyon yıl süreyi aşkın gelişen bir evreni modellemeye fizikçiler için olanak sağlar. Astronomik gözlemlerle birkaç parametreler(mesela evrenin madde yoğunluğu) sağlandıktan sonra ilaveten gözlemlenen veriler modelleri test etmek için kullanılabilir. Tahminler, ilkel nükleosentez, evrenin yüksek ölçekli yapısı, periyodunda oluşan ilk kimyasal elementlerin bolluğunu ve varlığını ve termal bir ekodan özelliklerini içerir. (kozmik özgeçmiş radyasyonu) Kozmolojik genişleme oranının astronomik gözlemleri, maddenin doğası gizemli kaldığı halde evrendeki toplam madde miktarının tahmin edilmesini sağlar. Bütün maddelerin yaklaşık %90 ı kara maddedir. (kütleye sahiptir fakat elektromanyetik olarak etkilemez ve bu yüzden direkt gözlemlenemez) Ana hatlarıyla bu yeni tür maddenin parçacık fiziği çatısında kabul edilmiş bir tanımı yoktur. Uzak Süpernovanın kızıla kayma incelemelerinden gözlemlenen kanıtlar ve özgeçmiş kozmik radyasyonun ölçümleri ayrıca kozmik genişlemenin ivmelenmesine ya da karanlık enerjiye neden olan kozmolojik sabitinden önemli derecede evrenin gelişiminin etkilendiğini gösterir. Yaklaşık saniye kozmik zamanında güçlü hızlandırılmış genişlemenin enflasyon safhası adlı yeni bir faz 1980 yılında klasik kozmolojik modeller ile açıklanamayan birkaç karışık gözlemlerin yararına varsayılmıştır. Son günlerdeki kozmik özgeçmiş radyasyonunun ölçümleri bu senaryo için ilk kanıtla sonuçlandı. Fakat geçerli gözlemler ile sınırlanamayan mümkün enflasyon senaryolarının şaşırtıcı bir çeşitliliği vardır. Enflasyon safhasına öncü ve büyük patlama tuhaflığını tahmin eden klasik modellere yakın en erken evrenin fiziği daha geniş bir sorudur. Otoriter cevap henüz geliştirilmemiş olan kuantum kütleçekimi teorisine gerek vardır.
İleri kavramlar[değiştir | kaynağı değiştir]
Global geometri ve sebep gösteren yapı[değiştir | kaynağı değiştir]

Genel görelilikte bir ışığın titreşimine hiçbir şey yetişemez ya da yakalayamaz. Işık A dan X e gönderilmeden A olayından hiçbir etki diğer X yerine ulaşamaz. Neticede bütün ışık hayat çizgilerinin (geçersiz jeodezik) keşfi uzay zamanın nedensel yapısı hakkında ana bilgiler verir. Bu yapı sınırlı bir haritaya oturtmak için uzayın sonsuz geniş alanları ve sonsuz zaman aralıklarının daraltılmış olduğu Penrose-Carter diyagramlarını kullanarak gösterilebilir. (ışık hala standart uzay zaman diyagramlarında olduğu gibi köşegenlere doğru hareket eder)
Nedensel yapının öneminin farkına varan Roger Penrose ve diğerleri neyin evrensel geometri olarak bilindiğini geliştirdiler. Evrensel geometride çalışmanın amacı Einstein’in denklemlerinin belli bir çözümü değildir. Bunun yerine bütün jeodezikler için doğru olan ilişkiler (Raychaudhuri denklemleri gibi) ve maddenin doğası (genelde enerji koşulları kalıbında kullanılır) hakkında özel olmayan varsayımlar genel sonuçları türetmek için kullanılır.
Ufuklar[değiştir | kaynağı değiştir]
Temel metin: Ufuk (genel görelilik ve kara delik mekaniği
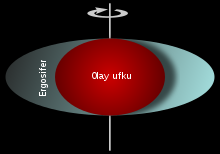
Evrensel geometriyi kullanarak bazı uzay zamanlar ufuklar olarak adlandırılan ve bir bölgeyi uzay zamanın geri kalanından ayıran, sınırları dâhil etmek için gösterilebilir. En iyi bilinen örnekleri kara deliklerdir: eğer kütle uzayın yeterince yoğun bir bölgesinde sıkıştırılırsa(ilgili ölçek uzunluğu Schwarzchild yarıçapı, halka hipotezi olarak tanımlı) içeriden dışarıya ışık çıkamaz. Bir ışık titreşimini hiçbir cisim geçemediği için içteki bütün madde de hapsolmuştur. Dışarıdan içeriye geçiş hala mümkündür. (bu da kara deliğin ufku yani sınırının fiziksel bir engel olmadığını gösterir)
Kara deliklerin eski çalışmaları Einstein’in denklemlerinin açık çözümlerine (özellikle statik bir kara deliği tanımlamak için kullanılan küresel olarak simetrik Schwarzschild çözümü ve dönen statik bir kara deliği tanımlamak ve dönen bir kara deliğin dışındaki bir bölge gibi ilginç özellikleri tanıştıran) simetrik eksenli yapılı Kerr çözümüne güvenildi. Evrensel geometriyi kullanarak sonraki çalışmalar kara deliklerin daha genel özelliklerini gösterdi. Bunlar, enerji, çizgisel moment, açısal moment, belir bir zamandaki yerİ ve elektrik yükünü belirten on bir parametre ile karakterize edilen daha basit cisimlerdir. Bu kara delik eşsizliği teoremi ile belirtilir. (‘’ kara delikler life sahip değildir, bu da insanların saçından bir farkının olmadığını işaret eder)Bir kara delik oluşturmak için çöken kütleçekimsel bir cismin karışıklığına bakmazsak cisim daha basit olur.
Daha önemli bir biçimde termodinamik yasasına benzeyen kara delik mekaniği olarak bilinen yasaların genel bir topluluğu vardır. Mesela kara delik mekaniğinin ikinci yasası (genel bir kara deliğin olay ufkusunun alanı zamanla hiç azalmayacaktır) termodinamik sistemin entropisine benzerdir. Bu, Penrose metodu kullanılarak dönen bir kara delikten klasik araçlar ile çıkartılabilen enerjiyi kısıtlar. Kara delik mekaniğinin aslında termodinamik yasasının bir altkümesi olması güçlü bir kanıttır. Bu da kara delik mekaniğinin orijinal yasalarının değişimine neden olur. Mesela kara delik mekaniğinin ikinci yasası termodinamiğin ikinci yasasının bir kısmı olduğu için özelikle entropi artarsa kara deliğin alanının azalması mümkündür. Sıfır sıcaklığa sahip olmayan termodinamik cisimlerde olduğu gibi kara delikler termal radyasyon salabilirler. Kısmen klasik hesaplamalar onların aslında Planck’in yasasında sıcaklık rolü oynayan yeryüzü kütleçekimi ile yapabildiğini gösterir. Bu radyasyon Hawking radyasyonu olarak bilinir.
Ufukların diğer türleri de vardır. Genişleyen bir evrende bir gözlemci, geçmişin bazı bölgelerinin (parçacık ufku) gözlemlenemeyeceğini ve geleceğin bazı bölgelerinin etkilenmeyeceğini (olay ufku) bulabilir. Minkowski uzayında bile ivmelenen gözlemci tarafından belirtildiğinde, Unruh radyasyonu olarak bilinen kısmen klasik bir radyasyon ile ilişkili ufuklar olacaktır.
Tuhaflıklar[değiştir | kaynağı değiştir]
Genel göreliliğin diğer genel bir özelliği tuhaflık olarak bilinen uzay zaman sınırlarının görünümüdür. Uzay zaman ışıksı ve zamansı jeodezikleri- serbest düşüşte ışık ve parçacıkların yol alabileceği bütün yollar- takip ederek araştırılabilir. Fakat bazı Einstein’in denklemlerinin sonuçları eksik kenarlara(ışığın ve düşen parçacıkların yolunun beklenmedik bir sona vardığı ve geometrinin tam tamamlanmamış olduğu bölge) sahiptir. Daha ilginç durumlarda bunlar, sonsuza kadar giden Ricci sabiti gibi uzay zamanın eğikliğini karakterize eden geometrik niceliklerin olduğu eğiklik tuhaflıklarıdır. Hayat çizgisinin bittiği gelecek tuhaflıkları ile uzay zamanın iyi bilinen örnekleri Schwarzchild çözümü(statik ölümsüz bir kara delik içindeki bir tuhaflığı tanımlayan) ya da ölümsüz ve dönen bir kara delik içindeki halka şeklindeki tuhaflıklara sahip Kerr çözümüdür. Evreni tanımlayan Friedmann-Lemaitre-Robertson-Walker çözümleri ve diğer uzay zamanlar Büyük Patlama isimli hayat çizgisinin başladığı eski tuhaflıklara sahiptir ve bazıları da Büyük Çöküş gibi tuhaflıklara sahiptir. Bu örneklerin fazlaca simetrik olduğu farz edersek (bu yüzlen kolaylaşır) tuhaflıklarının oluşumunun idealleşmenin bir yapaylığı olması caziptir. Evrensel geometrinin metotlarını kullanarak kanıtlanan ünlü tuhaflık teoremleri bunun dışında gerçekçi madde özelliklerine sahip bir maddenin çöküşü, mutlak bir evrede ve genişleyen evrenin geniş bir sınıfının başlangıcında gerçekleştikten sonra, tuhaflıkların genel göreliliğin kapsamlı bir geleceğini söyler. Fakat teoremler, biraz tuhaflıkların özellikleri hakkında ve daha çok kapsamlı yapıların varlıklarını karakterize etmeye adanmış geçerli araştırmalar(hipotezi kurulan BKL varsayım isimli örneği) hakkındadır. kozmik sansür hipotezi, bütün gelecek tuhaflıkları (harika bir simetrisi olmayan gerçek özellikli madde) güvenlice ufkunun arkasında saklanır ve bu yüzden bütün uzak gözlemcilere görünmezdir. Henüz düzgün bir kanıt olmamasına rağmen numarasal benzetmeler geçerliliğine destekleyici kanıtlar sunar.
Evrim denklemleri[değiştir | kaynağı değiştir]
Temel metin: İlk değeri formülleştirme (genel görelilik
Einstein’in denklemlerinin her bir çözümü bir evrenin bütün tarihini kuşatır. (şeylerin nasıl olduğunun sadece anlık bir fotoğrafı değildir; fakat bütün, mümkün ve madde dolu uzay zamandır) Her yerdeki geometrinin ve maddenin durumunu tarif eder. Genel eşdeğişkenlik nedeni ile Einstein’in teorisi kendince metrik tensörünün zaman evrimini saptaması için yeterli değildir. Koordinat koşulu ile birleştirilebilir. (diğer alan teorilerindeki kapsam sabitlemeye benzer) kısmi türevlenebilir denklemler olarak Einstein’in denklemlerini anlamak için onları evrenin evrimini tanımlayan bir yolda formülleştirmek yararlı olacaktır. Bu, uzay zamanın üç uzay boyutları ve bir zaman boyutuna bölündüğü "3+1" ile adlandırılan formüller ile yapılır. En bilinen örneği ADM biçimciliğidir. Bu bozulmalar, genel göreliliğin uzay zaman evrim denklemleri, ilk koşullar belirtildikten sonra iyi huyludur, her zaman vardır ve eşsizce tanımlıdır. Einstein’in alan denklemlerinin böyle formülleştirmeleri numarasal göreliliğin temelidir.
Evrensel ve hemen hemen yerel nitelikler[değiştir | kaynağı değiştir]
Evrim denklemlerinin görüşü derinden genel göreli fiziğin diğer yönü ile bağlanmıştır. Einstein’in teorisinde bir sistemin toplam kütlesi ya da enerjisi gibi görünüşte basit görünen genel bir tanım bulmak mümkün değildir. Temel nedeni, herhangi bir fiziksel alan gibi kütleçekimsel alan belli bir enerji ile verilmesidir; fakat o enerjiyi yerelleştirmenin imkânsız olduğunu temel olarak kanıtlar.
Yine de, kuramsal bir sonsuz uzak gözlemci ya da uygun simetrileri Komar kütlesi kullanarak bir sistemin toplam kütlesini tanımlamanın olasılıkları vardır. Eğer kütleçekimsel dalgalar ile enerjiyi sonsuza taşıyarak sistemin toplam kütlesinden dışarı çıkartırsak sonuç önemsiz sonsuzluktaki Bondi kütlesidir. Klasik fizikse olduğu gibi kütlelerin pozitif olduğu gösterilebilir. Evrensel tutarlı tanımlar momentum ve açısal momentum için vardır. Ayrıca o sistemi içeren uzayın sonlu bir bölgesinde tanımlanan nitelikleri kullanarak formülleştirilen izole edilmiş bir kütle gibi, hemen hemen yerel nitelikleri tanımlamak için birçok çaba vardır. Çember tahmininin daha hassas bir formülleştirmesi gibi izole edilmiş sistemler hakkındaki genel açıklamalar için, amaç yararlı bir nitelik elde etmektir.
Kuantum teorisi ile ilişki[değiştir | kaynağı değiştir]
Eğer genel görelilik, kuantum teorisi, modern fiziğin iki direğinden birisi olarak düşünülürse katı hal fiziğinden elementsel parçacıklara madde anlayışının temeli diğeridir. Fakat genel görelilik ile kuantum teorisinin fikirlerinin nasıl bağdaştırılacağı hala açık bir sorudur.
Eğri uzay zamanda kuantum alan teorisi[değiştir | kaynağı değiştir]
Temel metin: Eğik uzay zamanda kuantum teorisi Modern elementsel parçacık fiziğinin temelini oluşturan olağan kuantum alan teorileri, Dünyada bulunan kiler gibi zayıf yerçekimsel alanlarda mikroskobik parçacıkların davranışlarını tanımlarken mükemmel bir yaklaş olan Minkowski uzayını tanımlarlar. Kendisini niceleme ihtiyacı yeterince güçlü olmayan ve maddeyi etkilemen için kütleçekiminin yeterince güçlü olduğu yerdeki durumları tanımlamak için fizikçiler eğik uzay zamanda kuantum alan teorileri formüle ettiler. Bu teoriler, eğik özgeçmiş uzay zamanı tanımlamak için genel göreliliğe dayanır ve o uzay zamandaki kuantum maddesinin davranışını belirlemek için genelleştirilmiş kuantum alan teorisi tanımlar. Bu biçimciliği kullanarak kara deliklerin Hawking radyasyonu olarak bilinen parçacıkların kara cisim spektrumunu yayması gösterilebilir. (Hawking radyasyonu zamanla onların uçup giderek yol olacağı mümkün atını gösterir.) Yukarıdakilerin özeti olarak, bu radyasyon, kara deliklerin termodinamiği için önemli bir rol oynar.
Kuantum kütleçekimi[değiştir | kaynağı değiştir]
Temel metin: Kuantum yerçekimi
Ayrıca gör: İp teorisi, Standart genel görelilik, Kuantum kütleçekimi döngüsü ve Nedensel diziler
Tuhaflıkların görünmesinin yanı sıra(eğiklik uzunluk ölçeğinin mikroskobik olduğu zaman) maddenin kuantum tanımı ile uzay zamanın geometrik bir tanımı arasındaki tutarlılık için istek, kuantum kütleçekiminin tam bir teorisine olan ihtiyacı gösterir: kara deliklerin ve erken evrenin içinin yeterli bir tanımı ve kuantum fiziği dilinde uzay zamanın geometrisi ile ilişkili ve kütleçekimi varlığında bir teori için)

Temel etkileşimleri belirten elementsel parçacık fiziğinde kullanılan sıradan kuantum alan teorilerini genelleştirmek için bir girişim, kütleçekimini dâhil etmek için ciddi problemlere neden olur. Düşük enerjilerde bu yaklaşım, kabul edilebilir etkili kütleçekiminin kuantum alan teorisi ile sonuçlanan bir başarıyı kanıtlar. Fakat yüksek enerjilerde sonuçlar bütün kestirimci gücün model yokluğudur. (yeniden normalleştirilemememe)

Bu sınırlamaları yenmek için girişim nokta parçacıkların bir kuantum teorisi olmayan fakat minik bir boyutlu genişlemiş cisimlerin ip teorisidir. Bu teori, kütleçekimini içeren bütün parçacıkların ve etkileşimlerinin birleştirilmiş bir tanımı olacağına umut verir: bilinen üç boyuta ek olarak uzayın ek altı boyutları gibi anormal özelliklerin karşılığını vermek için bedel. İkinci süper ip devrinde ip teorisinin ve süpersimetri ile genel göreliliğin birleşimi M kuramı (tutarlı ve eşsiz tanımlı), kuantum kütleçekimi teorisi olarak bilinen on bir boyutlu model hipotezinin bir bölümünü oluşturduğu varsayıldı.
Diğer yaklaşım kuantum teorisinin standart niceleme işlemi ile başlar. Genel göreliliğin ilk-değer-formülleştirmesini kullanarak sonuç tam tamamlanmamış olan Wheeler-deWitt denklemidir. Fakat Ashtekar değişkenleri ile geleceği parlak kuantum kütleçekimi döngüsü modeli sağlanır. Uzay, fırıl (spin) ağı ile adlandırılan ve farklı adımları zamanla geliştiren ağ gibi bir yapı ile ifade edilir. Genel görelilik ve kuantum teorisinin hangi özelliklerinin kabul edilmiş ve hangi seviye değişikliklerinin tanıştırıldığına bağlı olarak dinamik üçgenleştirme, nedensel diziler, bükücü modeller ya da kuantum kozmolojisinin modellerine bağlı yol integralleri gibi geçerli bir kuantum teorisine ulaşmak için çok fazla başka girişimler vardır.
Bütün aday teoriler hala üstesinden gelinmesi gereken kavramsal ve biçimsel sorunlara sahiptir. Gelecekte parçacık fizik deneyleri ve kozmolojik gözlemler ile sağlanan bilgiler ile işe yarar bir umudun olmasına rağmen kuantum kütleçekimi tahminleri deneysel testlere koymanın henüz bir yolu yoktur. (bu yüzden tahminlerin değişikliğe uğradığı adaylar arasında da karar vermenin bir yolu yoktur.)
Geçerli durumlar[değiştir | kaynağı değiştir]
Genel görelilik bugüne kadar birçok kesin gözlemsel ve deneysel testler veren kozmoloji ve kütleçekimi modelinin fazlaca başarılı modelini ortaya çıkarmaktadır. Fakat teorinin tamamlanmadığını gösteren güçlü bulgular vardır. Kuantum kütleçekiminin ve uzay zaman tuhaflıklarının gerçeklikleri sorusu açık kalır. Kara madde ve kara enerji için kanıt olarak alınan gözlemsel bilgiler yeni bir fizik için ihtiyacı gösterir. Genel görelilik ileriki araştırmalar imkânınca zengindir. Matematiksel göreciler Einstein’in denklemlerinin temel özelliklerini ve tuhaflıkların doğasını anlamak için uğraşırlar ve artan bir şekilde güçlü bilgisayar simülasyonları (kara deliklerin birleşmesi gibi) kullanırlar. Kütleçekimsel dalgaların ilk direkt gözlemi için daha güçlü kütleçekimsel alanın geçerliliğini test etmek için fırsatları yaratma umudu ile yarış devam ediyor. Yayınından doksan yıl sonra genel görelilik araştırmaların yüksekçe bir aktif alanı olarak devam eder.
Ayrıca gör[değiştir | kaynağı değiştir]
Kaynakça[değiştir | kaynağı değiştir]
- ^ "Nobel Prize Biography". Nobel Prize. 23 Haziran 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 3 Ağustos 2012.
- ^ Pais 1982, ch. 9-15, Janssen 2005; birçok orijinal makalenin baskısını içeren, güncel bir koleksiyon Renn 2007; erişilebilir bir genel bakış Renn 2005, ss. 110. Erken dönemde yazılmış bir kilit makale Einstein 1907,Pais 1982, ch. 9. Alan denklemlerini ortaya koyan bir yayın Einstein 1915, Pais 1982, ch. 11–15
- ^ Schwarzschild 1916a, Schwarzschild 1916b ve Reissner 1916 (sonradan burada tamamlanmıştır Nordström 1918)
- ^ Einstein 1917, Pais 1982, ch. 15e
- ^ Hubble'ın orijinal makalesi Hubble 1929; erişilebilir bir genel bakış için Singh 2004, ch. 2–4
- ^ Gamow 1970
- ^ Pais 1982, ss. 253–254
- ^ Kennefick 2005, Kennefick 2007
- ^ Pais 1982, ch. 16
- ^ Thorne, Kip (2003). "Warping spacetime". The future of theoretical physics and cosmology: celebrating Stephen Hawking's 60th birthday. Cambridge University Press. s. 74. ISBN 0-521-82081-2. 31 Mayıs 2013 tarihinde kaynağından arşivlendi. Erişim tarihi: 3 Ağustos 2012., Sayfa 74 özeti 2 Haziran 2013 tarihinde Wayback Machine sitesinde arşivlendi.
- ^ Ehlers 1973, sec. 1
- ^ Arnold 1989, ch. 1
- ^ Ehlers 1973, ss. 5f














