Fourier serisi

Matematikte, Fourier serileri bir periyodik fonksiyonu basit dalgalı fonksiyonların (sinüs ve kosinüs) toplamına çevirir.
Fourier serileri, Joseph Fourier (1768-1830) tarafından bir metal çubuk veya levhadaki ısı denklemlerinin çözümü için kullanılmıştır. Fourier'in bu çalışmasından evvel, parçalı diferansiyel denklemlerle ifade edilen ısı denklemlerine genel bir çözüm yoktu. Her ne kadar parçalı yaklaşımlar olsa da yeterli değildi çünkü bu yaklaşımlar ısı dağılımının basit denklemlere göre dağıldığını varsayaraktan probleme yaklaşıyordu. (Mesela: Eğer ısı kaynağı bir sinüs veya kosinüs denklemiyse...) Bu temel/basit çözümler eigençözüm olarak adlandırılıyorlardı. Fourier'in düşüncesi basit denklemleri (sin ve cos) katsayılarla üst üste ekleyerek karmaşık ısı kaynağı kombinasyonları oluşturmaktı.
Fourier serileri ilk olarak ısı problemlerinin çözümü amacıyla kullanılmış olsa da bugün elektrik mühendisliğinde, titreşim analizinde, akustiklerde, sinyal işlemesinde, resim işlemesinde, kuantum mekaniğinde ve ekonomi hesaplamaları gibi birçok alanda kullanılmaktadır.
Konu hakkında ilk araştırmalar Leonhard Euler, Jean le Rond d'Alembert ve Daniel Bernoulli tarafından yapılmıştır. Fourier bu araştırma ve sonuçlarını ısı sorularına uygulamıştır ve ilk sonuçları Mémoire sur la propagation de la chaleur dans les corps solides adıyla 1807'de ve Théorie analytique de la chaleur adıyla 1822'de yayınlamıştır.
Dirichlet ve Riemann'ın katkılarıyla modern haline kavuşan Fourier Serileri, trigonometrik serilerde yaptığı önemli buluşlar sebebiyle Joseph Fourier (1768-1830) onuruna Fourier Serileri şeklinde adlandırılmıştır.
Tanım[değiştir | kaynağı değiştir]
ƒ(x) fonksiyonu, 2π periyodlu, gerçek değerli x'in fonksiyonudur. Bir başka deyişle tüm x değerleri için: ƒ(x + 2π) = ƒ(x).
Fourier'in periyodu 2π olan sinüs ve kosinüs fonksiyonlarını kullanarak yazılan formülü[değiştir | kaynağı değiştir]
P . periyodu ile bir periyodik fonksiyondur.Denkliğin kullanımı:

biz de bu eşdeğer formlarda fonksiyon yazabiliriz:
burada:
Eğer katsayılar (Fourier katsayıları olarak bilinir) aşağıdaki gibi hesaplanırsa:[1]
2π ile periyodik olan ve [−π, π] aralığında integrali alınabilen ƒ(x) fonksiyonu için,
ve
elemanları ƒ'in Fourier katsayıları olarak adlandırılır.
Böylece Fourier seri'nin ƒ için parçalı toplamı aşağıdaki gibi ifade edilir:
ƒ parçalı toplamları trigonometrik polinomlardır. Sonuç olarak N sonsuza yaklaştıkça SN ƒ, ƒ 'in gerçek değerine yaklaşır.
sonsuz toplamı ƒ' 'in Fourier serisidir.
Fourier serileri her zaman uzaksak değildir. Hatta uzaksak olduğunda bile bazen x'in bazı x0 değerlerinde serinin toplamı orijinal fonksiyon değerinden farklı sonuç verebilir. Burada akla önemli bir soru gelmektedir: Hangi kurala göre harmonik analizde seri şekline getirip getiremeyeceğimize karar vereceğiz? Eğer fonksiyonun [−π, π] aralığında integrali alınabiliyor ve değer sonsuzdan başka bir şey çıkıyorsa ve bu, tüm noktalarda oluyorsa Fourier serisi geçerlidir ve bulunabilir. Mühendislik uygulamalarında genelde fonksiyonda devamsızlık noktası olmadığı müddetçe fonksiyonun uzaksadığı varsayılır. Çünkü, mühendislikte karşılaşılan fonksiyonlar genelde matematikçilerin önerebileceği karşı-örneklere uzaktır ve daha iyi davranışlı fonksiyonlardır. Genel anlamda, Fourier serisi, ƒ(x) in türevinin karesinin (ki her yerde türevi olmayabilir) integrali alınabiliyorsa, kesinlikle uzaksaksar.[2]
Fourier katsayılarını daha genel fonksiyon ve dağılımlar için de kullanmak mümkündür. Ancak böyle durumlarda uzaksama veya zayıf uzaksama daha çok ilgi merkezidir.
-
Fourier serisinin alınan ilk 1,2,3 ve 4 terimleri ile bir kare dalganın yaklaşık bir diğer gösterimi
-
Yaklaşık bir gösterim için aynı genlik ve frekanstaki testere dişli bir dalganın karşılaştırılması
Örnek: basit bir Fourier serisi[değiştir | kaynağı değiştir]


Şimdi çok basit bir denklemin Fourier açılımının denklemini görelim. Bir testere-dişi dalgası düşünün:
Bu durumda, Fourier katsayıları,
gibidir.
Şu kesindir ki bu Fourier serisinin ƒ in türevinin alınabildiği tüm x değerlerinde, toplamı orijinal ƒ(x) fonksiyonuna yaklaşır ve sonunda ona eşit olur. Bundan dolayı:
x = π olduğunda, Fourier serisi 0 a eşit olur, ki bu ƒ in x = π deki sağdan ve soldan limitlerinin toplamının yarısına eşittir. Bu Fourier Serisi için Dirichlet teoreminde önemli bir noktadır.
Bakıyoruz ki Fourier serimizin açılımı ƒ(x) = x fonksiyonundan sadece azıcık daha karmaşıktır ve böyle bir serinin niçin kullanılabileceği de açıkçası hemencecik anlaşılacak bir şey değildir. Birçok uygulama alanı olmasıyla beraber biz Fourier serilerinin ısı denklemlerinin çözümündeki rolüne odaklanacağız. Örneğin, kenarları π uzunluğunda olan kare biçimindeki bir metal düşünün ve koordinatları (x, y) ∈ [0, π] × [0, π] olsun. Diyelim ki karenin 3 tarafı 0° derecede olsun ve y = π kenarı üzerinde sıcaklık denklemimiz T(x, π) = x olsun, ardından sabit/dengeye ulaşmış ısı dağılımının,
- denklemindeki gibi olduğunu görürüz.
Burada, sinh hiperbolik sinüs fonksiyonudur. Bu ısı denkleminin çözümü iki tarafın da ile Eq.1 çarpılmasıyla bulundu. Böyle bir denklemdeki Fourier serimiz her ne kadar basit de olsa ısı dağılımızın denklemi T(x, y) kesinlikle havadan, basit bir denklem değildir. Burada T kapalı formlu bir ifade şeklinde yazılamaz. Isı problemlerinin bu şekilde çözülebilmesi ancak Fourier'in çalışmasıyla mümkün olabilmiştir.
Fourier serilerinin bir diğer kullanım alanı da Parseval teoremi'yle Basel problem'lerinin çözümüdür. Örnek genelleşir ve ζ(2n) denklemini, n'in tüm pozitif tam sayı değerleri için çözmemiz gerekir.
Üstel Fourier serileri[değiştir | kaynağı değiştir]
Euler formülü'nü kullanarak,
Burada i kompleks sayıdır ve daha genel olan şu denklemi verir:
Fourier katsayıları da aşağıdaki gibidir:
an, bn, cn katsayıları da,
ve
gibi bağlantılıdır.
cn inin gösterimi birkaç Fourier fonksiyonun katsayılarını belirlemek için yetersizdir. Bundan dolayı isteğe göre ƒ in değişmiş bir hali olan(bizim örneğimizde) F veya
ile değiştirilir. Aynı zamanda fonksiyonel gösterim genelde yerine koyma yöntemiyle yapılır.
Böylece:
Mühendislikte, x zamanı ifade ettiğinde katsayı dizisi Frekans domain gösterimi olarak adlandırılır. Fonksiyondaki kare parantezler fonksiyonun discrete(devamsız) frekans seti olduğunu ifade eder.
Genel Bir [a, b] aralığında Fourier Serileri[değiştir | kaynağı değiştir]
Aşağıdaki formül, uygun komplex değerli, G[n] fonksiyonu
için, bütün R: da τ ile periyodik bir fonksiyondur.
Eğer fonksiyonumuzun karesinin integrali [a, a + τ] aralığında alınabiliyorsa bu aralıkta, fonksiyonumuz yukarıdaki formülle ifade edilebilir. Eğer g(x) in integrali alınabiliyorsa Fourier katsayıları,
şeklinde olur.
Dikkat etmeniz gereken şu ki: ifade edilen fonksiyon τ ile periyodiktir. Böylece a rastgele b,r sayıdır ve en popüler değerler a = 0 ve a = −τ/2 dir.
Sıklıkla kullanılan bir diğer frekans domain gösterimi de Fourier serisi katsayılarını Dirac comb fonksiyonunu modüle etmek için kullanılır:
ƒ değişkeni sürekli bir frekans domain'i ifade eder. x değişkeni
x değişkeni saniye cinsinden olduğu yerlerde ƒ hertz cinsindendir. Testere dişi dalgasının "dişleri" 1/τ'nin tam katlarındadır, ki bunlar temel frekansın harmonikleri olarak adlandırılırlar. Orijinal g(x) fonksiyonu seri tanım fonksiyonunun ters Fourier dönüşümüyle elde edilebilir:
Periyodik bir fonksiyonun Fourier integrali yakınsak olmasa da,G(ƒ) fonksiyonu yaygın olarak Fourier dönüşümü olarak anılır.[3]
Bir kare dalga üzerinde Fourier serisi[değiştir | kaynağı değiştir]
Aynı zamanda [−π, π]×[−π, π] aralığında Fourier serilerini iki (x ve y) değişkenli bir fonksiyon içinde tanımlayabiliriz :
Isı denklemleri gibi parçalı diferansiyel denklemlerin çözümü için kullanılmasının dışında, Fourier serilerinin bir diğer dikkate değer uygulaması da görüntü sıkıştırma alanındadır. Bilhassa, jpeg görüntü sıkıştırma standartları kosinüs temel fonksiyonlarını kullanan bir Fourier dönüşümü olan iki boyutlu ayrık kosinüs dönüşümünü kullanır.
- 29 Aralık 2009 tarihli İngilizce vikipedideki Fourier Series makalesinden çevrilmiştir.
Başlangıçlar[değiştir | kaynağı değiştir]
Devrim niteliğindeki makale[değiştir | kaynağı değiştir]
| “ |
İki tarafı da ile çarpıp ve sonra den e integralini aldığımızda:
|
„ |
—30px, 30px | ||
Bu modern yaklaşıma oldukça yakın olan birkaç satırda Fourier'in yaptığı bu denklemler fizik ve matemetikte devrim niteliğinde etki bırakmıştır. Her ne kadar burada kullanılan trigonometrik denklem ve seriler daha önceleri Euler, d'Alembert, Daniel Bernoulli ve Gauss tarafından kullanılmış olsa da Fourier bu denklemlerin sıradan, karmaşık dalga çeşitlerinin de bu serilerle gösterilebileceğini gösterir.
Bu teorinin kullanımı daha önceleri epey karmaşık olan uzaksak seriler, fonksiyon uzayı ve harmonik analizinde önemli yenilik ve kolaylıklar getirmiştir.
Fourier bu çalışmasını 1807'de komiteye gösterdiğinde -ki komitede Lagrange, Laplace, Malus ve Legendre gibi önemli isimler vardı- ...yazarın bu denklemlere ulaşmadaki yolu karmaşıklıktan ve zorluktan tamamen uzak olup[...] onun analiz için sentezleri basitlik ve genellik bakımından şiddetli bir hayranlık uyandıracak seviyededir. diyerek yorumlarlar.
Harmonik analizin doğuşu[değiştir | kaynağı değiştir]
Fourier'in zamanından beri Fourier serilerinin konseplerini tanımlamak ve anlamak için birçok farklı yaklaşım keşfedildi. Bu keşiflerin her biri asıl teoriyi destekler ve konunun farklı noktalarına vurgu yapacak mahiyetteydi. Fourier bu orijinal çalışmayı yaparken henüz bilinmeyen, keşfedilmeyen birçok matematiksel işlevi olan denklemle daha sonraları çok güçlü ve seçkin yaklaşımlar keşfedildi. Fourier asıl makalesinde sadece gerçek değerli Sinüs ve kosinüs denklemlerini kullanmıştı.
Bunların en önemlisi kompleks değerli üstel fonksiyonlar dır ve eixko şeklinde ifade edilirler. Aynı zamanda komleks harmonikler olarak adlandırılır ve harmonik analizin temelidir.
Fourier serileriyle ilgili birçok transform da farklı yaklaşımlara ve fikirlere genişletilecek şekilde keşfedilmiş ve kullanılmıştır. Bunlardan en önemlileri Fourier dönüşümü ve Z-dönüşümüdür.
Uzantılar[değiştir | kaynağı değiştir]
Bir kare üzerinde Fourier serisi[değiştir | kaynağı değiştir]
kare [−π, π]×[−π, π] içinde x ve y iki değişkenin fonksiyonları için Fourier serisi tanımlanabilir :
Isı denklemi gibi kısmi diferansiyel denklemlerin çözümü için kullanışlı olduğu bir yana kare üzerinde Fourier serisinin tek kayda değer uygulaması imaj baskısı içindedir. Özel olarak, jpeg imaj baskı standardında iki-boyutlu ayrık cos dönüşümü kullanılır, burada bir Fourier transformu cos taban fonksiyonları kullanılıyor.
Bravais-kafes-periodik-fonksiyonunun Fourier serisi[değiştir | kaynağı değiştir]
Bravais kafesi formun vektörlerinin kümesi olarak tanımlanabilir:
Burada ni tam sayıdır ve ai üç doğrusal bağımsız vektörlerdir.Bazı fonksiyonlar varsayalım, f(r), böylece herhangi Bravais kafes vektör R: f(r) = f(r + R) için durum aşağıdakine uyar,bunun bir Fourier serisi yapılabilir.Fonksiyonun bu türü, örneğin,bu etkin potansiyel bir elektronu bir periyodik kristal içinde "hissedebilir". Bu potansiyelin bir Fourier serisi yapmak için yararlı ise Bloch teoremi uygulanıyor. Birincisi,kafesin koordinat-sistemi içinde herhangi keyfi vektör r yazabiliriz:
burada ai = |ai|.
Böylece yeni bir fonksiyon tanımlayabiliriz,
Bu yeni fonksiyon, ,şimdi üç-değişikliklerin bir fonksiyonudur,bunun her a1, a2 periyodisite var, a3 sırasıyla: .
x1 içinde [0, a1] aralığı üzerinde g için bir serisi yazılırsa,aşağıdakini tanımlayabilir:
Ve o zaman:
yazabiliriz
Daha ileri tanım:
Biz bir kez daha g yazabilir:
Nihayet üçüncü koordinat için aynısı uygulanarak tanımlanır:
g gibi yazarız:
Yeniden düzenlenmesi:
Şimdi, her karşıt kafes vektör olarak yazılabilir,burada li tam sayı ve gi karşıt kafes vektörlerdir, aslında 'yi herhangi K keyfi karşıt kafes vektör için hesaplamaya kullanabiliriz ve r,uzayı içinde keyfi vektör,burada skaler çarpım:
Ve bu yüzden bizim genişletme, toplam karşılıklı kafes vektörleri üzerinde gerçek olduğu açıktır:
burada
Varsayalım
Orijinal kartezyen koordinat sistemi içinde hacim elementi hesabı için derece içinde x1, x2 ve x3'in terimleri içinde x, y ve z için doğrusal üç denklemin bu sistemi çözülabilir. önce x1'in terimleri içinde x, y ve z var, x2 ve x3,Jakobiyen determinant hesaplanabilir:
Bazı hesaplama ve olmayan bazı önemsiz çapraz çarpım kimliklerini uygulamadan sonra eşit olduğu gösterilmiştir edilebilir:
(Bu hesaplamalar bir kartezyen koordinat sistemi gibi içinde çalıştığı için basitleştirme uğruna avantajlı olabilir,o sadece çok olur ki bu a1 x eksenine paraleldir, tüm x-y düzlemi içinde yatan a2 ve a3 üç eksenin bileşenleri var). Paydadaki ilkel birim hücrenin hacmi tamdır bu a1, a2 ve a3 üç ilkel-vektörlerii ile kapalıdır. Özellikle, şimdi şunu biliyoruz
Biz ilkel hücrenin hacmi üzerinde geleneksel koordinat sisteminin hacmi üzerinde bir integral olarak şimdi h(K) yazabiliriz,x1, x2 ve x3 değişikliklerin yerine:
Ve C ilkel birim hücredir, böylece, ilkel birim hücrenin hacmidir.
Özellikler[değiştir | kaynağı değiştir]
Riemannyen manifoldlar[değiştir | kaynağı değiştir]

Domen bir grup değilse, o zaman hiçbir içsel tanımlanmış evrişim yoktur.X tıkız bir Riemann manifoldu ise o zaman Laplace-Beltrami işlemcisi bulunmaktadır.Laplace-Beltrami operatöre analoji baglantilar ile, bir X'te ısı denklemleri düşünebilirsiniz Sonra Riemann manifoldu X için Laplace operatörünün karşılık diferansiyel operatörü Fourier ısı denklemin, çözmeye çalışırken onun tabanından gelmesinden dolayı, doğal genellemeye esas olarak Laplace-Beltrami operatörü özçözümleri kullanılmaktır. Bu X bir Riemann manifoldu olup L2(X) tipinin uzayı için genelleniyor, mekânlar için Fourier serilerini yaygınlaştırıyor.Fourier serileri benzer şekillerde [−π, π] durumunda yakınsar. Tipik bir örnek olarak, Fourier taban küresel harmonikleri oluşur ki bu durumda, her zamanki gibi metrik ile küre biçiminde X almaktır.
Ayrıca bakınız[değiştir | kaynağı değiştir]
- Matematiksel fonksiyonların listesi
- Ayrık Fourier dönüşümü
- Hızlı Fourier dönüşümü
- Laurent serisi –veya karşıt olarak q = eix konularak bir Laurent serisi içinde bir Fourier serisi dönüşümü,bu j-değişmezi nin q-seri açılımı içinde kullanılıyor.
- Jean-Baptiste Joseph Fourier
- Fourier dönüşümü
Kaynakça[değiştir | kaynağı değiştir]
- ^ Dorf, Richard C.; Tallarida, Ronald J. (15 Temmuz 1993). Pocket Book of Electrical Engineering Formulas. 1. Boca Raton,FL: CRC Press. ss. 171-174. ISBN 0849344735.
- ^ Georgi P. Tolstov (1976). Fourier Series (İngilizce). Courier-Dover. 0486633179. 3 Mayıs 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 29 Aralık 2009.
- ^ Fourier dönüşümünün integral tanımı yakınsak olmadığından, periyodik fonksiyonu ve dönüşüm fonksiyonunu dağılım olarak algılamak lazım. Bu açıdan dağılıma bir örnek olan Dirac delta fonksiyonudur.












![{\displaystyle (S_{N}f)(x)={\frac {a_{0}}{2}}+\sum _{n=1}^{N}\,[a_{n}\cos(nx)+b_{n}\sin(nx)],\quad N\geq 0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cff74f4cc63376278745fc298c28130ff8939164)
![{\displaystyle {\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\,[a_{n}\cos(nx)+b_{n}\sin(nx)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a48744c1b526b072c67a1cd69300f9cebc58f5b3)
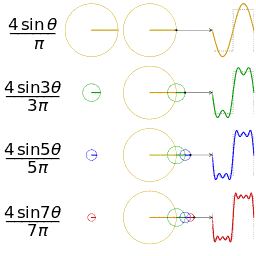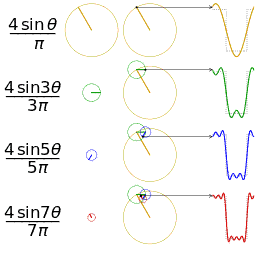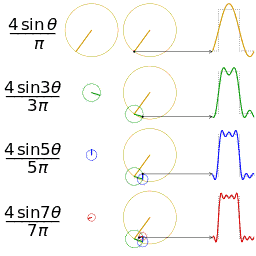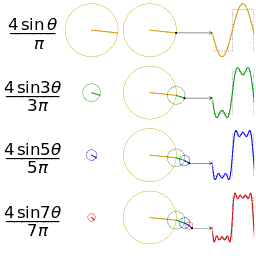




![{\displaystyle {\begin{aligned}f(x)&={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[a_{n}\cos \left(nx\right)+b_{n}\sin \left(nx\right)\right]\\&=2\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \mathrm {for} \quad x-\pi \notin 2\pi \mathbf {Z} .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df331d3a65b3f8e9b23673e8c41ed3e215d1ae4a)








![{\displaystyle {\begin{aligned}f(x)&=\sum _{n=-\infty }^{\infty }{\hat {f}}(n)\cdot e^{inx}\\&=\sum _{n=-\infty }^{\infty }F[n]\cdot e^{inx}\quad {\mbox{(mühendislik)}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0ebd764cade06c5683f2bd88f0f1dee7aaf33f7)
![{\displaystyle g(x)=\sum _{n=-\infty }^{\infty }G[n]\cdot e^{i2\pi {\frac {n}{\tau }}x}\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cf67b9b6885604eae08291e8373e0463fa6494d)
![{\displaystyle G[n]={\frac {1}{\tau }}\int _{a}^{a+\tau }g(x)\cdot e^{-i2\pi {\frac {n}{\tau }}x}\,dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/127fd3604e5aeb3bafeb12fa9b478573efe03112)
![{\displaystyle G(f)\ {\stackrel {\mathrm {def} }{=}}\ \sum _{n=-\infty }^{\infty }G[n]\cdot \delta \left(f-{\frac {n}{\tau }}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b39a114a078b6c280b2b3a0524aa8acace8a774)
![{\displaystyle {\begin{aligned}{\mathcal {F}}^{-1}\{G(f)\}&={\mathcal {F}}^{-1}\left\{\sum _{n=-\infty }^{\infty }G[n]\cdot \delta \left(f-{\frac {n}{\tau }}\right)\right\}\\&=\sum _{n=-\infty }^{\infty }G[n]\cdot \underbrace {{\mathcal {F}}^{-1}\left\{\delta \left(f-{\frac {n}{\tau }}\right)\right\}} _{e^{i2\pi {\frac {n}{\tau }}x}\cdot \underbrace {{\mathcal {F}}^{-1}\{\delta (f)\}} _{1}}\\&=\sum _{n=-\infty }^{\infty }G[n]\cdot e^{i2\pi {\frac {n}{\tau }}x}\quad =\ \ g(x).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/940d750c29d30ce793c227a057e80575f7d6e47d)















![{\displaystyle {\begin{aligned}h^{\mathrm {two} }(m_{1},m_{2},x_{3})&:={\frac {1}{a_{2}}}\int _{0}^{a_{2}}h^{\mathrm {one} }(m_{1},x_{2},x_{3})\cdot e^{-i2\pi {\frac {m_{2}}{a_{2}}}x_{2}}\,dx_{2}\\[12pt]&={\frac {1}{a_{2}}}\int _{0}^{a_{2}}dx_{2}{\frac {1}{a_{1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left({\frac {m_{1}}{a_{1}}}x_{1}+{\frac {m_{2}}{a_{2}}}x_{2}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b375ad1bad97e4cee6cfa9c82d20582af5ba6b4)

![{\displaystyle {\begin{aligned}h^{\mathrm {three} }(m_{1},m_{2},m_{3})&:={\frac {1}{a_{3}}}\int _{0}^{a_{3}}h^{\mathrm {two} }(m_{1},m_{2},x_{3})\cdot e^{-i2\pi {\frac {m_{3}}{a_{3}}}x_{3}}\,dx_{3}\\[12pt]&={\frac {1}{a_{3}}}\int _{0}^{a_{3}}dx_{3}{\frac {1}{a_{2}}}\int _{0}^{a_{2}}dx_{2}{\frac {1}{a_{1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left({\frac {m_{1}}{a_{1}}}x_{1}+{\frac {m_{2}}{a_{2}}}x_{2}+{\frac {m_{3}}{a_{3}}}x_{3}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bac3a4c30ff78f3abc70b6b65a6274b8899ca038)








![{\displaystyle {\begin{bmatrix}{\dfrac {\partial x_{1}}{\partial x}}&{\dfrac {\partial x_{1}}{\partial y}}&{\dfrac {\partial x_{1}}{\partial z}}\\[3pt]{\dfrac {\partial x_{2}}{\partial x}}&{\dfrac {\partial x_{2}}{\partial y}}&{\dfrac {\partial x_{2}}{\partial z}}\\[3pt]{\dfrac {\partial x_{3}}{\partial x}}&{\dfrac {\partial x_{3}}{\partial y}}&{\dfrac {\partial x_{3}}{\partial z}}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5095a317a5c0975c5d1bdf27cd79d13b106a96a6)




