Isı motoru
Bu madde hiçbir kaynak içermemektedir. (Nisan 2014) (Bu şablonun nasıl ve ne zaman kaldırılması gerektiğini öğrenin) |
Bu madde, Vikipedi biçem el kitabına uygun değildir. (Nisan 2014) |
| Termodinamik |
|---|
 |
Termodinamikte, ısı enerjisini mekanik enerjiye çeviren sistemlere Isı Motoru denir. Bu çeviriyi maddeyi çok yüksek sıcaklıklara getirip daha sonra düşük sıcaklıklara getirerek yapar. Isınan madde jeneratörün devinimsel kısmında "iş" yaparak enerjisini jeneratöre aktarır ve soğur. Bu işlem esnasında bir miktar termal enerji "iş"e dönüşür. Dönüşüm miktarı kullanılan maddeye bağlıdır.
kullanılan madde ısı kapasitesi "0" olmayan herhangi bir madde olabilir ancak genellikle sıvı veya gazlar kullanılır.
Genellikle motorlar enerjiyi mekanik "iş"'e çevirirler. Ancak ısı motorları kendilerini bu tip motorlardan verimliliklerinin Carnot kuramı ile sınırlı olmasından dolayı ayırırlar ama bu limitleme tersine çevrilebilr. Isı motorlarının en büyük avantajı pek çok enerjinin egzotermik reaksiyonlarla(yanma reaksiyonları gibi), ışığın soğurulması ile ve sürtünmeyle kolaylıkla ısı enerjisine çevrilebilmesidir.
Isı motorları genellikle döngülerle karıştırılır.

Termodinamikte ısı motorları çoğu zaman "Otto döngüsü" gibi standart mühendislik döngüleri ile modellenir.
Kuramsal modeller gerçek motorlardan çalışma esnasında alınan verilerle oluşturulur. Ancak motor uygulamalarının pek azı altında yatan termodinamik döngüleriyle gerçekten uyuşur.
Genel terimlerle, ısı farkı ne kadar çok ise, teral verim o kadar fazladır. Dünya üzerinde herhangi bir ısı motorunun soğuk kısmı çevresel etkiler tarafından limitlenmiştir. yani 300 kelvinden daha düşük bir sıcaklıkta olamaz. Bu nedenle ısı motorlarının verimini arttırmaya yönelik çalışmalar genelde bu limiti esnetebilmek veya ortadan kaldırabilmek üzerine yapılmaktadır.
En çok kuramsal ısı motor verimi (hiçbir motor bu verime ulaşamamaktadır) sıcak ve soğuk kısmın sıcaklık farklarının sıcak kısmın sıcaklığına bölümü ile bulundan değerdir (sıcaklık değerleri kelvin cinsinden olmalıdır)
Güç[değiştir | kaynağı değiştir]
Isı motorları spesifik güçleri tarafından karakterize edilirler. Bu litre başına verilen Kw(beygir gücü olarak da geçebilir) güçlerine göre ayrım anlamına gelir. Ancak bu ayrım benzin kullanım verimiyle karıştırılmamalıdır. Modern yüksek performanslı bir araba 1 litre benzinden 75 kW güç elde edebilir.
- Isı Motoru Örnekleri
- Faz değişim döngüleri
Bu sistemlerde genellikle sıvı ve gaz kullanılır. Motor kullanılan sıvıyı gaza, kullanılan gazı sıvıya dönüştürür. bunların kisini de yapabilir.
• Rankine döngüsü
• İyileştirici döngü (regenerative cycle)
• Organik rankine döngüsü
• Buhardan sıvıya döngü
• Sıvıdan katıya döngü
• Katıdan gaza döngü
Gibi türevleri vardır.
- Sadece gaz içeren döngüler
• Carnot döngüsü
• Ericsson döngüsü
• Stirling döngüsü
• İçten yanmalı motorlar
• Otto döngüsü (benzin/petrol motorları9
• Dizel döngüsü
• Atkinson döngüsü
• Joule döngüsü
• Lenoir döngüsü
• Miller döngüsü
- Sadece sıvı içeren döngüler
• Malone motoru
• Rejeneratif ısı döngüsü (Heat Regenerative Cyclone)
- Elektron döngüleri
• Johnson termoelektrik enerji dönüştürücüsü
• Termoelektrik (Peltier-Seebeck etkisi)
• Termoiyonik emisyon
• Termotünel soğutma
- Manyetik döngüler
• Termo-manyetik motor (Nikola Tesla)
- Soğutma amaçlı kullanılan döngüler (buzdolapları vs)
• Buhar sıkıştırmalı soğutma
• Stirling dondurucuları (stirling cryocoolers)
• Gaz soğurmalı soğutma
• Hava döngüsü makinesi
• Vuilleumier soğutma
• Manyetik soğutma
Verim[değiştir | kaynağı değiştir]
Isı motorlarında verim giren enerjiye göre ne kadar çıkarn enerji elde edildiğiyle hesaplanır
- Burada;
- Motor tarafından yapılan işin miktarıdır. Eksi olmasının sebebi motorun iş yapmasıdır.
- yüksek sıcaklıktaki sistemden alınan ısı enerjisidir
- düşük sıcaklıktaki sisteme verilern ısı enerjisidir.
Genel olarak ısı aktarım süreçlerinde (motor soğutucu veya ısı pompası olması önemli değil) verim "ne verdin? " "ne aldın?" oranıdır.
en çok verim için ise;
Burada;
- ısı kaynağının kelvin cinsinden kesin sıcaklığı de ısının aktarıldığı "küvetin" (sink) kelvin cinsinden kesin sıcaklığıdır.
Verim için bir örnek vermemiz gerkirse
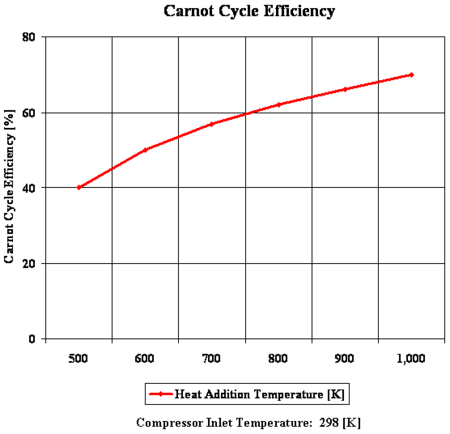 |
 |
Bu tablolarda Carnot döngüsündeki verim farklılıkları gösterilmiştir. 1. grafikte eklenen ısı enerjisi ile verimdeki artışı göstermektedir. 2. grafikte ise ısı ret sıcaklığındaki bir artış ile verimin nasıl değiştiği gösterilmektedir.























