Coulomb kanunu
| Elektromanyetizma |
|---|
 |
Coulomb yasası, ya da Coulomb’un ters kare yasası, bir fizik yasasıdır. Elektrik yüklü tanecikler arasındaki elektrostatiği tanımlar. Bu yasa 1785'te Fransız fizikçi Charles Augustin de Coulomb tarafından yayınlanmıştır ve klasik elektromanyetizmadaki önemli bir gelişmedir. Coulomb yasası Gauss yasasından ve vice versa(bahsi geçen hadisenin tam tersinin de geçerli olduğunu anlatmak için kullanılır)dan türetilmiştir. yasa elektromanyetizmin prensibi durumuna gelmiştir.
Tarihçe[değiştir | kaynağı değiştir]

Antik Akdeniz toplumlarında, kehribar çubuğunun kedi kürküne sürtüldüğünde tüy gibi hafif nesneleri çektiği bilinirdi. MÖ 600'de Miletli Thales statik elektrik üzerine bir takım gözlemler yaptı. Gördüğü şeyi, sürtünmenin mıknatıs görevi gördüğüne yordu. Buna karşın manyetit gibi minerallerin sürtünmeye ihtiyacı yoktu.[1][2] Thales, bu çekim olayının manyetik alandan dolayı olduğu konusunda yanılıyordu fakat bilim daha sonra manyetizma ve elektriklenme arasında bir bağlantı olduğunu kanıtladı. Elektrik 17. Yüzyıla kadar bir merak olarak kalmıştır. Ardından William Gilbert adında bir İngiliz bilim insanı, mıknatıs taşını kehribarla sürterek oluşan statik elektrikle ilgili elektrik ve manyetizma hakkında araştırmalar yaptı[1] ve bilime Latince bir kelime kazandırdı: electricus. Electricus küçük objelerin sürtündükten sonra birbirini çekme özelliği anlamına geliyordu.[3] Bu kelime İngilizcede electric ve electricity kelimelerini çağrıştırıyordu ve Thomas Browne’ nin 1646’da kurulmuş olan Pseudodoxia Epidemica’sının ilk baskısında görülmüştü.[4] 18. Yüzyılın ilk araştırmacıları, elektriksel kuvvetin yerçekim kuvveti olayında olduğu gibi(ters kare yasası) uzaklıkla azaldığını saptamışlardır. Elektrikle yüklenmiş olan küreler üzerinde yapılan deneylere dayanarak, İngiliz bilim insanı Joseph Priestley ise elektriksel kuvvetin ters kare yasasına uyduğunu ileri süren ilk kişiydi. Fakat bu konunun detaylarına inemedi.[5][6][7]

1769’da İskoç fizikçi John Robison, yüklü iki cismin birbirini itmesi olayının aynı işaretli yüklerle olduğunu deneylerinde gözlemlediğini duyurdu.[8] 1770'lerin başında İngiliz bilim insanı Henry Cavendish, yüklü iki cismin arasındaki kuvvetin bağlı olduğu yük ve uzaklık olgusunu keşfetmişti fakat bu keşfi hiçbir yazılı kaynakta yer almamıştı.[9] Sonunda 1785'te Fransız fizikçi Charles-Augustin de Coulomb, elektrik ve manyetizma hakkında yazdığı ilk üç raporunda bu yasanın kendi yasası olduğunu belirtti. Yayınlanan bu raporlar elektromanyetizmanın temeli sayılmıştır.[10] Charles-Augustin de Coulomb yüklü cisim arasında itme ya da çekmeyi saptamak için burulma terazisini kullanmıştır. Daha sonra noktasal iki yükün arasındaki elektriksel kuvvetin yükle doğru, uzaklığın karesiyle ters orantılı olduğunu saptamıştır.
Yasa[değiştir | kaynağı değiştir]
Coulomb yasası der ki:
- İki noktasal yükün arasındaki elektrostatik kuvvet yüklerin skaler çarpımıyla doğru, aralarındaki uzaklığın karesiyle ters orantılıdır . [10]
- Bu iki cismin yüklerinin işaretleri eğer aynı ise(pozitif-pozitif gibi) birbirlerini iterler, eğer farklıysa birbirlerini çekerler .

Coulomb yasası aynı zamanda basit bir matematik eşitliği gösterir.
- ve
Coulomb sabitidir (), ve yük büyüklükleridir, skalerdir ve yüklerin arasındaki uzaklıktır, vektörel olarak yüklerin arasındaki uzaklıktır ve . kuvvetini bularak, tarafından uygulanan üzerindeki kuvveti bulmuş oluruz. Eğer kullanılmış olsa, o zaman da üzerindeki kuvvet bulunmuş olunurdu. Bu kural Newton'un üçüncü yasası için de kullanılmaktadır: .
Birimler[değiştir | kaynağı değiştir]
Elektromanyetik teori açıklanırken genellikle Uluslararası Birimler Sistemi kullanılır. Kuvvet Newton (birim) ile ölçülür, yük coulomb ile ve uzaklık metre birimiyle ölçülür. Coulomb sabiti ile gösterilir. yalıtkanlık sabitidir ve birimi C2 m−2 N−1. Ve bağıl yalıtkanlık sabitidir. Elektrik alanın birimi ise birim metredeki voltdur.
Elektrik alanı[değiştir | kaynağı değiştir]
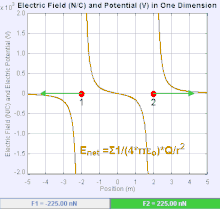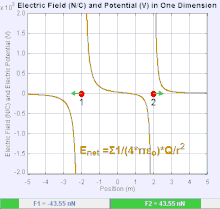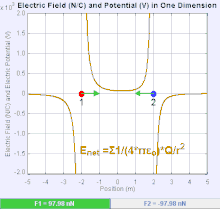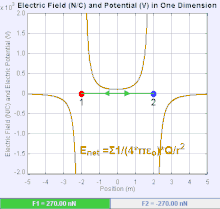
Elektrik alanı bir vektör alanıdır. Coulomb kuvveti, uzaydaki her test yükü ile bağdaştırılır. Daha basitçe, elektrik alanı basit bir noktasal yük kaynağı üretilir. Coulomb kuvvetinin büyüklüğü ve yönü , test yükü üzerindeki, elektrik alanına bağlı olarak, eşitliği ile bulunur. Elektrik alanı çizgileri düz çizgilerdir ve pozitif yüklü cisimde, cismin merkezinden dışarı doğru iken, negatif yüklü cismde çizgiler dışarıdan cismin merkezine doğrudur. Elektrik alanı Coulomb yasasından türetilir. Boşlukta bir test yükü ve noktasal yük kaynağı seçildiğinde, oluşan elektrik alanı noktasal yük kaynağı tarafından oluşur ve formülüze edilmiş şekli ise:
- .
Coulomb sabiti[değiştir | kaynağı değiştir]
Coulomb sabiti Coulomb yasasında bir orantı faktörü olarak yer almaktadır ayrıca elektrikle ilgili birçok formülde yer almaktadır. ile gösterilir. Aynı zamanda elektrik kuvveti sabiti ya da elektrostatik sabiti diye de anılmaktadır. Coulomb sabitinin tam değeri:
Yasanın geçerli olması için koşullar[değiştir | kaynağı değiştir]
Coulomb yasasının geçerli olabilmesi için iki koşul gerekmektedir.
- Yükler, noktasal yük olmalıdır.
- Yükler birbirlerine göre hareketsiz olmak zorundadır.

Skaler formu[değiştir | kaynağı değiştir]
Skaler formu demek, kuvvetin sadece büyüklüğünü bulmaya yöneliktir yani yönü hesaba katılmamaktadır. Sadece büyüklüğü ve işaretiyle ilgilenildiğinde kuvvetinin ve üzerindeki anlık etkisi: aradaki uzaklık, Coulomb sabitidir. çarpım sonucu eğer pozitif çıkarsa birbirlerini itiyor demektir. Eğer sonuç negatif çıkarsa yükler birbirlerini çekiyor demektir.[11]
Vektör formu[değiştir | kaynağı değiştir]

Vektör olan tarafından oluşur,diğer vektör de tarafından oluşur. olduğu zaman cisimler birbirini iter (resimde olduğu gibi), olduğu zaman ise cisimler birbirini çeker. Kuvvetler her zaman birbirine eşit olur. Coulomb yasasına göre kuvvetinin, pozisyonunda ve herhangi bir diğer yük olan , pozisyonunda eşitliği:
, birim vektörleri ve elektrik sabiti. Coulomb yasasının vektör formu, birim vektörün yönü ile yasanın basitçe skaler tanımı , den e paralel çizgidir.[12] Eğer iki yük değeri aynı işaret ise, yük çarpımları pozitif olacaktır ve üzerindeki kuvvetin yönü şeklinde olacaktır. Yükler birbirlerini itecektir. Eğer yükler zıt işaretlelerse skaler çarpımı negatif olur ve üzerindeki kuvvetin yönü şeklinde olur. Yükler birbirini çekecektir. Newton’un üçüncü yasasına göre, elektrostatik kuvvet , den oluşmaktadır. şeklinde gösterilmektedir.
Ayrık yükler sistemi[değiştir | kaynağı değiştir]
Üst üste gelim ilkesi(örtüşüm ilkesi) Coulomb yasasın içerdiği yük sayısını istenilen sayıda olmasına izin vermektedir. Yüklü cisimler nedeniyle oluşan herhangi bir yük üzerindeki kuvvet, basitçe diğer yükler üzerine etki eden kuvvetlerin vektörel toplamı ile bulunur. Bulunan kuvvet toplamı elektrik alanına paraleldir. Boşluktaki ayrık sistem nedeniyle, pozisyonundaki üzerindeki kuvveti:
'ninci yükün sırasıyla ve büyüklük ve pozisyonudur. birim vektör ve yönü ise; (yönü ise den a doğrudur).[12]
Sürekli yük dağılımı[değiştir | kaynağı değiştir]
Bu konuda doğrusal üst üste gelim ilkesi kullanılır. Sürekli yük dağılımında, integral kullanılır. Çünkü sonsuz küçük sayıdaki parça noktasal yük gibi davranır ve sonsuz sayıdaki noktasal yükün kuvveti de integral yoluyla bulunur. Bu yük dağılımı doğrusal, alansal ya da hacimseldir. Doğrusal yük dağılımında (telin içindeki yük için ideal yaklaşımdır) bize konumunda, uzunluğunun sonsuz küçük parçasında, birim uzunluktaki yük miktarını verir.
- .[13]
Alansal yük dağılımında (paralel kondansatörler için ideal yaklaşımdır), bize pozisyonunda, sonsuz küçük alan içinde, birim alandaki yük miktarını verir.
Hacimsel yük dağılımında (mesela hacimsel bir metal kütlede), bize konumunda, sonsuz küçük hacimde, birim hacimdeki yük miktarını verir.
Boşlukta konumundaki küçük test yükü olan yük dağılımdaki integral ile bulunur.
Coulomb yasasını doğrulamaya yönelik basit deney[değiştir | kaynağı değiştir]

Coulomb yasasını basit bir deneyle doğrulamak mümkündür. İki küçük küre düşünelim. Kütlesi olsun, yükleri ise aynı işaretli ve olsun. uzunluğunda ve kütlesi ihmal edilen iki halattan sarkıtılmış olsunlar. Her bir küre üzerine etki eden kuvvet üç tanedir bunlar: Ağırlık , halat gerilimi ve elektrik kuvvvettir . Denge konumundan:
|
|
(1 ) |
Ve
|
|
(2) |
Eşitlik (1), eşitlik (2)’ye bölündüğünde:
|
|
(3) |
küreler arasındaki uzaklık, kürelerin birbirine yaptığı itme kuvveti
|
|
(Coulomb Yasası) |
Yani:
|
|
(4) |
Eğer yüklerden birisinin yükünü boşaltırsak ve yüklü olan diğer cisimle biribirine değdirirsek her birinin kazanacağı yük olacaktır. Denklik durumuna göre, olacaktır ve aralarında itme kuvveti ise:
|
|
(5) |
olduğunu biliyoruz. Ve:
Eşitlik (4), eşitlik (5)’e bölündüğünde:
|
|
(6) |
Uygulamada, açıların ölçülmesi zordur. Eğer halatları boyları yeteri kadar uzun olursa, açı aşağıdaki yaklaşımlardaki sonuç gibi küçük olacaktır:
|
|
(7) |
Eşitlik (6) kullanılarak daha basit bir sonuç elde edilecektir:
|
|
(8) |
Sonsuz küçük sürattaki yayılmanın geçici delili[değiştir | kaynağı değiştir]
2012’nin sonunda, INFN'nin deneycileri, elektron demeti ile algıçlar arasındaki kuvvetin yayılmasında gecikme olmadığını gösterdi.[14] Deney sonucun doğruluğunun kanıtlanması halen beklenmesine rağmen, Aberasyon Coulomb yasasında geçerli olmadığını gösterdi.
Elektrostatik yaklaşım[değiştir | kaynağı değiştir]
Coulomb yasasının geçerli olma koşulları, yüklerin hareketsiz kalması ve çok yavaş hareket etmeleridir. Bu koşullar elektrostatik yaklaşım olarak bilinir. Hareket yer aldığı zaman, iki yükün oluşturduğu kuvveti manyetik alan değiştirir.
Atomik kuvvet[değiştir | kaynağı değiştir]
Coulomb yasası, atomun çekirdeğindeki pozitif yük ile elektronlardaki negatif yük arasındaki kuvveti de tanımlamaktadır. Bu yasa genel olarak, molekülleri oluşturan atomlar arasındaki kuvvet, sıvı ile katı formundaki maddeleri oluşturan atomlar ve moleküller arasındaki kuvveti açıklar. İyonlar arasındaki uzaklık arttıkça, çekim enerjisi sıfıra yaklaşır. Farklı işaretli yüklerin büyüklükleri arttıkça enerji artar.
Ayrıca bakınız[değiştir | kaynağı değiştir]
Kaynakça[değiştir | kaynağı değiştir]
- ^ a b Stewart, Joseph (2001). Intermediate Electromagnetic Theory. World Scientific. s. 50. ISBN 981-02-4471-1Şablon:İnconsistent citations
- ^ Simpson, Brian (2003). Electrical Stimulation and the Relief of Pain. Elsevier Health Sciences. ss. 6-7. ISBN 0-444-51258-6Şablon:İnconsistent citations
- ^ Baigrie, Brian (2006). Electricity and Magnetism: A Historical Perspective. Greenwood Press. ss. 7-8. ISBN 0-313-33358-0Şablon:İnconsistent citations
- ^ Chalmers, Gordon (1937). "The Lodestone and the Understanding of Matter in Seventeenth Century England". Philosophy of Science. 4 (1). ss. 75-95. doi:10.1086/286445Şablon:İnconsistent citations
- ^ Schofield, Robert E. (1997). The Enlightenment of Joseph Priestley: A Study of his Life and Work from 1733 to 1773. University Park: Pennsylvania State University Press. ss. 144-56. ISBN 0-271-01662-0.
- ^
Priestley, Joseph (1767). The History and Present State of Electricity, with Original Experiments. Londra. s. 732.
May we not infer from this experiment, that the attraction of electricity is subject to the same laws with that of gravitation, and is therefore according to the squares of the distances; since it is easily demonstrated, that were the earth in the form of a shell, a body in the inside of it would not be attracted to one side more than another?
- ^ Elliott, Robert S. (1999). Electromagnetics: History, Theory, and Applications. ISBN 978-0-7803-5384-8. 10 Mart 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 12 Haziran 2014.
- ^ Robison, John (1822). Murray, John (Ed.). A System of Mechanical Philosophy. 4. Londra.
On page 68 8 Şubat 2015 tarihinde Wayback Machine sitesinde arşivlendi., the author states that in 1769 he announced his findings regarding the force between spheres of like charge. On page 73 1 Aralık 2016 tarihinde Wayback Machine sitesinde arşivlendi., the author states the force between spheres of like charge varies as x-2.06:
When making experiments with charged spheres of opposite charge the results were similar, as stated on page 73 1 Aralık 2016 tarihinde Wayback Machine sitesinde arşivlendi.:The result of the whole was, that the mutual repulsion of two spheres, electrified positively or negatively, was very nearly in the inverse proportion of the squares of the distances of their centres, or rather in a proportion somewhat greater, approaching to x-2.06.
Nonetheless, on page 74 1 Aralık 2016 tarihinde Wayback Machine sitesinde arşivlendi. the author infers that the actual action is related exactly to the inverse duplicate of the distance:When the experiments were repeated with balls having opposite electricities, and which therefore attracted each other, the results were not altogether so regular and a few irregularities amounted to 1/6 of the whole; but these anomalies were as often on one side of the medium as on the other. This series of experiments gave a result which deviated as little as the former (or rather less) from the inverse duplicate ratio of the distances; but the deviation was in defect as the other was in excess.
On page 75 1 Aralık 2016 tarihinde Wayback Machine sitesinde arşivlendi., the authour compares the electric and gravitational forces:We therefore think that it may be concluded, that the action between two spheres is exactly in the inverse duplicate ratio of the distance of their centres, and that this difference between the observed attractions and repulsions is owing to some unperceived cause in the form of the experiment.
Therefore we may conclude, that the law of electric attraction and repulsion is similar to that of gravitation, and that each of those forces diminishes in the same proportion that the square of the distance between the particles increases.
- ^ Maxwell, James Clerk, (Ed.) (1967). "Experiments on Electricity: Experimental determination of the law of electric force.". The Electrical Researches of the Honourable Henry Cavendish... (1.1özgünyıl=1879 bas.). Cambridge, England: Cambridge University Press. ss. 104-113.
On pages 111 and 112 the author states:We may therefore conclude that the electric attraction and repulsion must be inversely as some power of the distance between that of the 2 + 1/50 th and that of the 2 - 1/50 th, and there is no reason to think that it differs at all from the inverse duplicate ratio.
- ^ a b In -- Coulomb (1785a) "Premier mémoire sur l’électricité et le magnétisme," 22 Nisan 2014 tarihinde Wayback Machine sitesinde arşivlendi. Histoire de l’Académie Royale des Sciences, pages 569-577 -- Coulomb studied the repulsive force between bodies having electrical charges of the same sign:
Page 574 : Il résulte donc de ces trois essais, que l'action répulsive que les deux balles électrifées de la même nature d'électricité exercent l'une sur l'autre, suit la raison inverse du carré des distances.
In -- Coulomb (1785b) "Second mémoire sur l’électricité et le magnétisme," 1 Ocak 2014 tarihinde Wayback Machine sitesinde arşivlendi. Histoire de l’Académie Royale des Sciences, pages 578-611. -- Coulomb showed that oppositely charged bodies obey an inverse-square law of attraction.Translation : It follows therefore from these three tests, that the repulsive force that the two balls --[that were] electrified with the same kind of electricity -- exert on each other, follows the inverse proportion of the square of the distance.
- ^ Coulomb's law 13 Nisan 2019 tarihinde Wayback Machine sitesinde arşivlendi., Hyperphysics
- ^ a b c Coulomb's law 9 Temmuz 2015 tarihinde Wayback Machine sitesinde arşivlendi., University of Texas
- ^ Charged rods 10 Ekim 2014 tarihinde Wayback Machine sitesinde arşivlendi., PhysicsLab.org
- ^ Calcaterra, A.; de Sangro, R.; Finocchiaro, G.; Patteri, P.; Piccolo, M.; Pizzella, G. (2012). "Measuring Propagation Speed of Coulomb Fields". arXiv:1211.2913 $2.
Ek kaynaklar[değiştir | kaynağı değiştir]
- Coulomb, Charles Augustin (1788) [1785]. "Premier mémoire sur l'électricité et le magnétisme". Histoire de l’Académie Royale des Sciences. Imprimerie Royale. ss. 569-577.
- Coulomb, Charles Augustin (1788) [1785]. "Second mémoire sur l'électricité et le magnétisme". Histoire de l’Académie Royale des Sciences. Imprimerie Royale. ss. 578-611.
- Griffiths, David J. (1998). Introduction to Electrodynamics (3.3 yayıncı=Prentice Hall bas.). ISBN 0-13-805326-X.
- Tipler, Paul A.; Mosca, Gene (2008). Physics for Scientists and Engineers (6.6 yayıncı=W. H. Freeman and Company bas.). New York. ISBN 0-7167-8964-7. LCCN 2007010418.
- Young, Hugh D.; Freedman, Roger A. Sears and Zemansky's University Physics : With Modern Physics (13.13 yıl = 2010 bas.). Addison-Wesley (Pearson). ISBN 978-0-321-69686-1.
Dış bağlantılar[değiştir | kaynağı değiştir]
- Coulomb's Law14 Mayıs 2017 tarihinde Wayback Machine sitesinde arşivlendi. on Project PHYSNET14 Mayıs 2017 tarihinde Wayback Machine sitesinde arşivlendi.
- Electricity and the Atom21 Şubat 2009 tarihinde Wayback Machine sitesinde arşivlendi.-a chapter from an online textbook
- A maze game for teaching Coulomb's Law 13 Ekim 2014 tarihinde Wayback Machine sitesinde arşivlendi.-a game created by the Molecular Workbench software
- Electric Charges, Polarization, Electric Force, Coulomb's Law14 Mart 2009 tarihinde Wayback Machine sitesinde arşivlendi. Walter Lewin, 8.02 Electricity and Magnetism, Spring 2002: Lecture 1 (video). MIT OpenCourseWare. License: Creative Commons Attribution-Noncommercial-Share Alike.














































































![{\displaystyle {\frac {L_{1}}{L_{2}}}\approx 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}\Longrightarrow {\frac {L_{1}}{L_{2}}}\approx {\sqrt[{3}]{4}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c9166e7d5f120fd7a63a5c035838dbe36df9dcf)