1 − 2 + 3 − 4 + · · ·: Revizyonlar arasındaki fark
| [kontrol edilmemiş revizyon] | [kontrol edilmemiş revizyon] |
k Bot değişikliği Ekleniyor: sv:1 − 2 + 3 − 4 + · · · |
Superyetkin (mesaj | katkılar) Değişiklik özeti yok |
||
| 1. satır: | 1. satır: | ||
{{Çeviri}} |
|||
{{Çalışma var}} |
|||
[[Dosya:Pm1234 Ground.png|thumb|1 − 2 + 3 − 4 + …'ün ilk binlik bölümünün kısmi toplamı]] |
[[Dosya:Pm1234 Ground.png|thumb|1 − 2 + 3 − 4 + …'ün ilk binlik bölümünün kısmi toplamı]] |
||
[[Matematik]]te |
[[Matematik]]te '''1 − 2 + 3 − 4 + · · ·''' sınırsız bir [[Dizi (terim)|dizi]]dir. Bu dizi art arda gelen pozitif [[Tam sayılar|tam sayılar]]ın verilen sırayla değişimini gösterir. [[Toplama|Sigma toplama gösterimi]]ni kullanarak serinin ilk m teriminin toplamı şöyle ifade edilebilir: |
||
:<math alt="Summation from n equals 1 to m of the series n * (-1)^(n-1)">\sum_{n=1}^m n(-1)^{n-1}.</math> |
:<math alt="Summation from n equals 1 to m of the series n * (-1)^(n-1)">\sum_{n=1}^m n(-1)^{n-1}.</math> |
||
Iraksak |
Iraksak (kısmi toplamlar sırası 1, −1, 2, −2, · · · biçiminde süren) diziler herhangi bir sınıra yakınsamazlar. Bu, 1 − 2 + 3 − 4 + · · · dizisinin ıraksadığı biçiminde de ifade edilebilir. |
||
Tüm bunlara karşın, [[Leonhard Euler]] 18. yüzyılın ortalarında bu dizinin [[Paradoks|mantığa aykırı görünen]] bir denklem olduğunu öne sürmüştür. |
|||
:<math alt="1-2+3-4+...=1/4">1-2+3-4+\cdots=\frac{1}{4}.</math> |
:<math alt="1-2+3-4+...=1/4">1-2+3-4+\cdots=\frac{1}{4}.</math> |
||
Bu denklemin doğru açıklaması |
Bu denklemin doğru açıklaması daha sonraki yıllarda da tartışma konusu olmuştur. [[1980]]'lerin başlarında Ernesto Cesàro, Émile Borel ve diğerleri, farklı diziyle genellenen toplamları ifade etmesi için Euler'in denemelerinin yeni yorumlarını kapsayan iyi tanımlanmış yöntemler geliştirmeye çalışmışlardır. Bu toplanabilirlik yöntemlerinin birçoğu 1 − 2 + 3 − 4 + · · · toplamının {{frac|1|4}}'e eşit olduğunu öne sürmektedir. Cesàro toplamı 1 − 2 + 3 − 4 + · · ·'e yaklaşık da olsa bir değer atayamayan az sayıdaki yöntemden biridir. Bu, Abel toplamı gibi daha sağlam sonuçlar veren yöntemlerin kullanılmasını zorunlu kılmaktadır. |
||
1 − 2 + 3 − 4 + |
1 − 2 + 3 − 4 + · · · dizisi, Grandi'nin dizisi 1 − 1 + 1 − 1 + · · · ile yakından ilintilidir. |
||
== Iraksaklık == |
== Iraksaklık == |
||
Dizinin her bir elemanı (1, −2, 3, −4, |
Dizinin her bir elemanı (1, −2, 3, −4, · · ·) hem '''+''' hem de '''−''' yönde [[Sıfır|0]]'dan uzaklaşmaktadır; bu yüzden 1 − 2 + 3 − 4 + · · ·, [[terim testi]] ile ayrılır. Bu yöntem, bir noktada birleşmesiyle ya da sınırsız bir dizinin ayrılmasıyla, bir sonsuz serinin ıraksaklığını belirlemenin basit bir yöntemidir. Başka bir deyişle, 1 − 2 + 3 − 4 + · · ·'ün kısmi toplamları: |
||
:1 = '''1''', |
:1 = '''1''', |
||
:1 − 2 = '''−1''', |
:1 − 2 = '''−1''', |
||
| 24. satır: | 27. satır: | ||
:1 − 2 + 3 − 4 + 5 = '''3''', |
:1 − 2 + 3 − 4 + 5 = '''3''', |
||
:1 − 2 + 3 − 4 + 5 − 6 = '''−3''', |
:1 − 2 + 3 − 4 + 5 − 6 = '''−3''', |
||
:· · · |
|||
:… |
|||
biçiminde ifade edilebilir. |
|||
{{matematik-taslak}} |
|||
==Heuristics for summation== |
|||
===Stability and linearity=== |
|||
Since the terms 1, −2, 3, −4, 5, −6, … follow a simple pattern, the series {{nowrap|1 − 2 + 3 − 4 + …}} can be manipulated by shifting and term-by-term addition to yield a numerical value. If it can make sense to write {{nowrap|1=''s'' = 1 − 2 + 3 − 4 + …}} for some ordinary number ''s'', the following manipulations argue for {{nowrap|1=''s'' = {{frac|1|4}}:}}<ref>Hardy (p.6) presents this derivation in conjunction with evaluation of [[Grandi's series]] {{nowrap|1 − 1 + 1 − 1 + …}}.</ref> |
|||
<math> |
|||
\begin{array}{rclllll} |
|||
4s&=& &(1-2+3-4+\cdots) & +(1-2+3-4+\cdots) & +(1-2+3-4+\cdots) &+(1-2+3-4+\cdots) \\ |
|||
&=& &(1-2+3-4+\cdots) & +1+(-2+3-4+5+\cdots) & +1+(-2+3-4+5+\cdots) &-1+(3-4+5-6\cdots) \\ |
|||
&=&1+[&(1-2-2+3) & +(-2+3+3-4) & +(3-4-4+5) &+(-4+5+5-6)+\cdots] \\ |
|||
&=&1+[&0+0+0+0+\cdots] \\ |
|||
4s&=&1 |
|||
\end{array} |
|||
</math> |
|||
[[Image:Pm1234 linearity.svg|thumb|right|Adding 4 copies of {{nowrap|1 − 2 + 3 − 4 + …,}} using only shifts and term-by-term addition, yields 1. The left side and right side each demonstrates two copies of {{nowrap|1 − 2 + 3 − 4 + …}} adding to {{nowrap|1 − 1 + 1 − 1 + ….}}]] So <math>s=\frac{1}{4}</math>. This derivation is depicted graphically on the right. |
|||
Although 1 − 2 + 3 − 4 + … does not have a sum in the usual sense, the equation {{nowrap|1=''s'' = 1 − 2 + 3 − 4 + … = {{frac|1|4}}}} can be supported as the most natural answer if such a sum is to be defined. A [[generalization|generalized]] definition of the "sum" of a divergent series is called a [[summation method]] or [[summability method]], which sums some subset of all possible series. There are many different methods (some of which are described [[#Specific methods|below]]) that are characterized by the properties that they share with ordinary summation. What the above manipulations actually prove is the following: Given any summability method that is [[Divergent series#Properties of summation methods|linear and stable]] and sums the series {{nowrap|1 − 2 + 3 − 4 + …}}, the sum it produces is {{frac|1|4}}. Furthermore, since |
|||
<math> |
|||
\begin{array}{rcllll} |
|||
2s & = & &(1-2+3-4+\cdots) & + & (1-2+3-4+\cdots) \\ |
|||
& = & 1 + &(-2+3-4+\cdots) & + 1 - 2 & + (3-4+5\cdots) \\ |
|||
& = & 0 + &(-2+3)+(3-4)+ (-4+5)+\cdots \\ |
|||
2s & = & &1-1+1-1\cdots \\ |
|||
\end{array} |
|||
</math> |
|||
such a method must also sum [[Grandi's series]] as {{nowrap|1=1 − 1 + 1 − 1 + … = {{frac|1|2}}.}} |
|||
===Cauchy product=== |
|||
In 1891, [[Ernesto Cesàro]] expressed hope that divergent series would be rigorously brought into [[calculus]], pointing out, "One already writes {{nowrap|1=(1 − 1 + 1 − 1 + …)<sup>2</sup> = 1 − 2 + 3 − 4 + …}} and asserts that both the sides are equal to {{frac|1|4}}."<ref>Ferraro, p.130.</ref> For Cesàro, this equation was an application of a theorem he had published the previous year, one that may be identified as the first theorem in the history of summable divergent series. The details on his summation method are [[#Cesàro and Hölder|below]]; the central idea is that {{nowrap|1 − 2 + 3 − 4 + …}} is the [[Cauchy product]] of {{nowrap|1 − 1 + 1 − 1 + …}} with {{nowrap|1 − 1 + 1 − 1 + …}}. |
|||
[[Image:Pm1234 Cauchy.svg|thumb|left|1 − 2 + 3 − 4 + … as twofold Cauchy product of 1 − 1 + 1 − 1 + …]] |
|||
The Cauchy product of two infinite series is defined even when both of them are divergent. In the case where Σ''a''<sub>''n''</sub> = Σ''b''<sub>''n''</sub> = Σ(−1)<sup>''n''</sup>, the terms of the Cauchy product are given by the finite diagonal sums |
|||
:<math>\begin{array}{rcl} |
|||
c_n & = &\displaystyle \sum_{k=0}^n a_k b_{n-k}=\sum_{k=0}^n (-1)^k (-1)^{n-k} \\[1em] |
|||
& = &\displaystyle \sum_{k=0}^n (-1)^n = (-1)^n(n+1). |
|||
\end{array}</math> |
|||
The product series is then |
|||
:<math>\sum_{n=0}^\infty(-1)^n(n+1) = 1-2+3-4+\cdots.</math> |
|||
Thus a summation method that respects the Cauchy product of two series and sums {{nowrap|1=1 − 1 + 1 − 1 + … = {{frac|1|2}},}} will also sum {{nowrap|1=1 − 2 + 3 − 4 + … = {{frac|1|4}}}}. With the result of the previous section, this implies an equivalence between summability of {{nowrap|1 − 1 + 1 − 1 + …}} and {{nowrap|1 − 2 + 3 − 4 + …}} with methods that are linear, stable, and respect the Cauchy product. |
|||
Cesàro's theorem is a subtle example. The series {{nowrap|1=1 − 1 + 1 − 1 + …}} is Cesàro-summable in the weakest sense, called {{nowrap|(C, 1)-summable,}} while {{nowrap|1=1 − 2 + 3 − 4 + …}} requires a stronger form of Cesàro's theorem<ref>Hardy, p.3; Weidlich, pp.52–55.</ref>, being {{nowrap|(C, 2)-summable.}} Since all forms of Cesàro's theorem are linear and stable, the values of the sums are as we have calculated. |
|||
==Specific methods== |
|||
===Cesàro and Hölder=== |
|||
[[Image:Pm1234 means.svg|thumb|right|Data about the (H, 2) sum of {{frac|1|4}}]] |
|||
To find the (C, 1) [[Cesàro summation|Cesàro sum]] of 1 − 2 + 3 − 4 + …, if it exists, one needs to compute the [[arithmetic mean]]s of the partial sums of the series. |
|||
The partial sums are |
|||
:1, −1, 2, −2, 3, −3, …, |
|||
and the arithmetic means of these partial sums are |
|||
:1, 0, {{frac|2|3}}, 0, {{frac|3|5}}, 0, {{frac|4|7}}, …. |
|||
This sequence of means does not converge, so 1 − 2 + 3 − 4 + … is not Cesàro summable. |
|||
There are two well-known generalizations of Cesàro summation: the conceptually simpler of these is the sequence of (H, ''n'') methods for [[natural number]]s ''n''. The (H, 1) sum is Cesàro summation, and higher methods repeat the computation of means. Above, the even means converge to {{frac|1|2}}, while the odd means are all equal to 0, so the means ''of'' the means converge to the average of 0 and {{frac|1|2}}, namely {{frac|1|4}}.<ref>Hardy, p.9. For the full details of the calculation, see Weidlich, pp.17–18.</ref> So {{nowrap|1 − 2 + 3 − 4 + …}} is (H, 2) summable to {{frac|1|4}}. |
|||
The "H" stands for [[Otto Hölder]], who first proved in 1882 what mathematicians now think of as the connection between [[Divergent series#Abelian means|Abel summation]] and (H, ''n'') summation; {{nowrap|1 − 2 + 3 − 4 + …}} was his first example.<ref>Ferraro, p.118; Tucciarone, p.10. Ferraro criticizes Tucciarone's explanation (p.7) of how Hölder himself thought of the general result, but the two authors' explanations of Hölder's treatment of 1 − 2 + 3 − 4 + … are similar.</ref> The fact that {{frac|1|4}} is the (H, 2) sum of {{nowrap|1 − 2 + 3 − 4 + …}} guarantees that it is the Abel sum as well; this will also be proved directly below. |
|||
The other commonly formulated generalization of Cesàro summation is the sequence of (C, ''n'') methods. It has been proven that (C, ''n'') summation and (H, ''n'') summation always give the same results, but they have different historical backgrounds. In 1887, Cesàro came close to stating the definition of (C, ''n'') summation, but he gave only a few examples. In particular, he summed {{nowrap|1 − 2 + 3 − 4 + …,}} to {{frac|1|4}} by a method that may be rephrased as (C, ''n'') but was not justified as such at the time. He formally defined the (C, n) methods in 1890 in order to state his theorem that the Cauchy product of a (C, ''n'')-summable series and a (C, ''m'')-summable series is (C, ''m'' + ''n'' + 1)-summable.<ref>Ferraro, pp.123–128.</ref> |
|||
===Abel summation=== |
|||
[[Image:Pm1234 Abel.svg|thumb|left|120px|Some partials of 1−2''x''+3''x''<sup>2</sup>+…; 1/(1 + ''x'')<sup>2</sup>; and limits at 1]] |
|||
In a 1749 report, [[Leonhard Euler]] admits that the series diverges but prepares to sum it anyway: |
|||
{{blockquote|1=…when it is said that the sum of this series 1−2+3−4+5−6 etc. is {{frac|1|4}}, that must appear paradoxical. For by adding 100 terms of this series, we get –50, however, the sum of 101 terms gives +51, which is quite different from {{frac|1|4}} and becomes still greater when one increases the number of terms. But I have already noticed at a previous time, that it is necessary to give to the word ''sum'' a more extended meaning….<ref>Euler et al., p.2. Although the paper was written in 1749, it was not published until 1768.</ref>}} |
|||
Euler proposed a generalization of the word "sum" several times; see ''[[Euler on infinite series]]''. In the case of {{nowrap|1 − 2 + 3 − 4 + …,}} his ideas are similar to what is now known as [[Divergent series#Abelian means|Abel summation]]: |
|||
{{blockquote|1=…it is no more doubtful that the sum of this series 1−2+3−4+5 + etc. is {{frac|1|4}}; since it arises from the expansion of the formula {{frac|1|(1+1)<sup>2</sup>}}, whose value is incontestably {{frac|1|4}}. The idea becomes clearer by considering the general series 1 − 2''x'' + 3''x''<sup>2</sup> − 4''x''<sup>3</sup> + 5''x''<sup>4</sup> − 6''x''<sup>5</sup> + ''&c.'' that arises while expanding the expression {{frac|1|(1+''x'')<sup>2</sup>}}, which this series is indeed equal to after we set ''x'' = 1.<ref>Euler et al., pp.3, 25.</ref>}} |
|||
There are many ways to see that, at least for [[absolute value]]s |''x''| < 1, Euler is right in that |
|||
:<math>1-2x+3x^2-4x^3+\cdots = \frac{1}{(1+x)^2}.</math> |
|||
One can take the [[Taylor series|Taylor expansion]] of the right-hand side, or apply the formal [[polynomial long division|long division process for polynomials]]. Starting from the left-hand side, one can follow the general heuristics above and try multiplying by (1+''x'') twice or [[square (algebra)|squaring]] the [[geometric series]] {{nowrap|1 − ''x'' + ''x''<sup>2</sup> − ….}} Euler also seems to suggest [[derivative|differentiating]] the latter series term by term.<ref>For example, Lavine (p.23) advocates long division but does not carry it out; Vretblad (p.231) calculates the Cauchy product. Euler's advice is vague; see Euler et al., pp.3, 26. [[John C. Baez|John Baez]] even suggests a category-theoretic method involving multiply [[pointed set]]s and the [[quantum harmonic oscillator]]. Baez, John C. [http://math.ucr.edu/home/baez/qg-winter2004/zeta.pdf Euler's Proof That 1 + 2 + 3 + … = 1/12 (PDF).] math.ucr.edu (December 19, 2003). Retrieved on March 11, 2007.</ref> |
|||
In the modern view, the series 1 − 2''x'' + 3''x''<sup>2</sup> − 4''x''<sup>3</sup> + … does not define a [[function (mathematics)|function]] at {{nowrap|1=''x'' = 1,}} so that value cannot simply be substituted into the resulting expression. Since the function is defined for all {{nowrap||''x''| < 1,}} one can still take the limit as ''x'' approaches 1, and this is the definition of the Abel sum: |
|||
:<math>\lim_{x\rightarrow 1^{-}}\sum_{n=1}^\infty n(-x)^{n-1} = \lim_{x\rightarrow 1^{-}}\frac{1}{(1+x)^2} = \frac14.</math> |
|||
===Euler and Borel=== |
|||
[[Image:Pm1234 Euler.svg|right|thumb|Euler summation to {{frac|1|2}} − {{frac|1|4}}]] |
|||
Euler applied another technique to the series: the [[Binomial transform#Euler transform|Euler transform]], one of his own inventions. To compute the Euler transform, one begins with the sequence of positive terms that makes up the alternating series—in this case {{nowrap|1, 2, 3, 4, ….}} The first element of this sequence is labeled ''a''<sub>0</sub>. |
|||
Next one needs the sequence of [[difference operator|forward differences]] among {{nowrap|1, 2, 3, 4, …}}; this is just {{nowrap|1, 1, 1, 1, ….}} The first element of ''this'' sequence is labeled Δ''a''<sub>0</sub>. The Euler transform also depends on differences of differences, and higher [[iterated function|iterations]], but all the forward differences among {{nowrap|1, 1, 1, 1, …}} are 0. The Euler transform of {{nowrap|1 − 2 + 3 − 4 + …}} is then defined as |
|||
:<math>\frac12 a_0-\frac14\Delta a_0 +\frac18\Delta^2 a_0 -\cdots = \frac12-\frac14.</math> |
|||
In modern terminology, one says that {{nowrap|1 − 2 + 3 − 4 + …}} is [[Euler summation|Euler summable]] to {{frac|1|4}}. |
|||
The Euler summability implies another kind of summability as well. Representing {{nowrap|1 − 2 + 3 − 4 + …}} as |
|||
:<math>\sum_{k=0}^\infty a_k = \sum_{k=0}^\infty(-1)^k(k+1),</math> |
|||
one has the related everywhere-convergent series |
|||
:<math>a(x) = \sum_{k=0}^\infty\frac{(-1)^k(k+1)x^k}{k!} = e^{-x}(1-x).</math> |
|||
The [[Borel summation|Borel sum]] of 1 − 2 + 3 − 4 + … is therefore<ref>Weidlich p. 59</ref> |
|||
:<math>\int_0^\infty e^{-x}a(x)\,dx = \int_0^\infty e^{-2x}(1-x)\,dx = \frac12-\frac14.</math> |
|||
===Separation of scales=== |
|||
Saichev and Woyczyński arrive at {{nowrap|1=1 − 2 + 3 − 4 + … = {{frac|1|4}}}} by applying only two physical principles: ''infinitesimal relaxation'' and ''separation of scales''. To be precise, these principles lead them to define a broad family of "''φ''-summation methods", all of which sum the series to {{frac|1|4}}: |
|||
*If ''φ''(''x'') is a function whose first and second derivatives are continuous and integrable over (0, ∞), such that φ(0) = 1 and the limits of φ(''x'') and ''x''φ(''x'') at +∞ are both 0, then<ref>Saichev and Woyczyński, pp.260–264.</ref> |
|||
::<math>\lim_{\delta\rightarrow0}\sum_{m=0}^\infty (-1)^m(m+1)\varphi(\delta m) = \frac14.</math> |
|||
This result generalizes Abel summation, which is recovered by letting ''φ''(''x'') = exp(−''x''). The general statement can be proved by pairing up the terms in the series over ''m'' and converting the expression into a [[Riemann integral]]. For the latter step, the [[Summation of Grandi's series#Separation of scales|corresponding proof]] for {{nowrap|1 − 1 + 1 − 1 + …}} applies the [[mean value theorem]], but here one needs the stronger Lagrange form of [[Taylor's theorem]]. |
|||
==Generalizations== |
|||
[[Image:Pm1234 Euler1755 I-V.png|thumb|Euler sums similar series in the 1755 ''Institutiones'']] |
|||
The threefold Cauchy product of {{nowrap|1 − 1 + 1 − 1 + …}} is {{nowrap|1 − 3 + 6 − 10 + …,}} the alternating series of [[triangular number]]s; its Abel and Euler sum is {{frac|1|8}}.<ref>Kline, p.313.</ref> The fourfold Cauchy product of {{nowrap|1 − 1 + 1 − 1 + …}} is {{nowrap|1 − 4 + 10 − 20 + …,}} the alternating series of [[tetrahedral number]]s, whose Abel sum is {{frac|1|16}}. |
|||
Another generalization of 1 − 2 + 3 − 4 + … in a slightly different direction is the series {{nowrap|1 − 2<sup>''n''</sup> + 3<sup>''n''</sup> − 4<sup>''n''</sup> + …}} for other values of ''n''. For positive integers ''n'', these series have the following Abel sums:<ref>Knopp, p.491; there appears to be an error at this point in Hardy, p.3.</ref> |
|||
:<math>1-2^{n}+3^{n}-\cdots = \frac{2^{n+1}-1}{n+1}B_{n+1}</math> |
|||
where ''B''<sub>''n''</sub> are the [[Bernoulli number]]s. For even ''n'', this reduces to |
|||
:<math>1-2^{2k}+3^{2k}-\cdots = 0.</math> |
|||
This last sum became an object of particular ridicule by [[Niels Henrik Abel]] in 1826: |
|||
:"Divergent series are on the whole devil's work, and it is a shame that one dares to found any proof on them. One can get out of them what one wants if one uses them, and it is they which have made so much unhappiness and so many paradoxes. Can one think of anything more appalling than to say that |
|||
::0 = 1 − 2<sup>''n''</sup> + 3<sup>''n''</sup> − 4<sup>''n''</sup> + etc. |
|||
:where ''n'' is a positive number. Here's something to laugh at, friends."<ref>Grattan-Guinness, p.80. See Markushevich, p.48, for a different translation from the original [[French language|French]]; the tone remains the same.</ref> |
|||
Cesàro's teacher, [[Eugène Charles Catalan]], also disparaged divergent series. Under Catalan's influence, Cesàro initially referred to the "conventional formulas" for {{nowrap|1 − 2<sup>''n''</sup> + 3<sup>''n''</sup> − 4<sup>''n''</sup> + …}} as "absurd equalities", and in 1883 Cesàro expressed a typical view of the time that the formulas were false but still somehow formally useful. Finally, in his 1890 ''Sur la multiplication des séries'', Cesàro took a modern approach starting from definitions.<ref>Ferraro, pp.120–128.</ref> |
|||
The series are also studied for non-integer values of ''n''; these make up the [[Dirichlet eta function]]. Part of Euler's motivation for studying series related to {{nowrap|1 − 2 + 3 − 4 + …}} was the [[functional equation]] of the eta function, which leads directly to the functional equation of the [[Riemann zeta function]]. Euler had already become famous for finding the values of these functions at positive [[even and odd numbers|even integers]] (including the [[Basel problem]]), and he was attempting to find the values at the positive [[even and odd numbers|odd integers]] (including [[Apéry's constant]]) as well, a problem that remains elusive today. The eta function in particular is easier to deal with by Euler's methods because its [[Dirichlet series]] is Abel summable everywhere; the zeta function's Dirichlet series is much harder to sum where it diverges.<ref>Euler et al., pp.20–25.</ref> For example, the counterpart of {{nowrap|1 − 2 + 3 − 4 + …}} in the zeta function is the non-alternating series {{nowrap|[[1 + 2 + 3 + 4 + · · ·|1 + 2 + 3 + 4 + …]]}}, which has deep applications in modern [[physics]] but requires much stronger methods to sum. |
|||
==Notlar== |
|||
{{reflist|2}} |
|||
==Kaynakça== |
|||
*{{cite book |last=Beals |first=Richard |title=Analysis: an introduction |year=2004 |publisher=Cambridge UP |isbn= 0-521-60047-2}} |
|||
*{{cite book |last=Davis |first=Harry F. |title=Fourier Series and Orthogonal Functions |year=1989 |month=May |publisher=Dover |isbn= 0-486-65973-9}} |
|||
*{{cite web |author=Euler, Leonhard; Lucas Willis; and Thomas J Osler |title=Translation with notes of Euler's paper: Remarks on a beautiful relation between direct as well as reciprocal power series |year=2006 |publisher=The Euler Archive |url=http://www.math.dartmouth.edu/~euler/pages/E352.html |accessdate=2007-03-22}} Originally published as {{cite journal |last=Euler |first=Leonhard |title=Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques |journal=Memoires de l'academie des sciences de Berlin |year=1768 |volume=17 |pages=83–106}} |
|||
*{{cite journal |last=Ferraro |first=Giovanni |title=The First Modern Definition of the Sum of a Divergent Series: An Aspect of the Rise of 20th Century Mathematics |journal=Archive for History of Exact Sciences |year=1999 |month=June |volume=54 |issue=2 |pages=101–135 |doi=10.1007/s004070050036}} |
|||
*{{cite book |last=Grattan-Guinness |authorlink=Ivor Grattan-Guinness |first=Ivor |year=1970 |title=The development of the foundations of mathematical analysis from Euler to Riemann |publisher=MIT Press |isbn= 0-262-07034-0}} |
|||
*{{cite book |last=Hardy |first=G.H. |authorlink=G. H. Hardy |title=Divergent Series |year=1949 |publisher=Clarendon Press |id={{LCCN|91|0|75377}}}} |
|||
*{{cite journal |last=Kline |first=Morris |authorlink=Morris Kline |title=Euler and Infinite Series |journal=Mathematics Magazine |volume=56 |issue=5 |year=1983 |month=November |pages=307–314 |url=http://links.jstor.org/sici?sici=0025-570X%28198311%2956%3A5%3C307%3AEAIS%3E2.0.CO%3B2-M}} |
|||
*{{cite book |first=Shaughan |last=Lavine |title=Understanding the Infinite |year=1994 |publisher=Harvard UP |isbn= 0674920961}} |
|||
*{{cite book |last=Markushevich |first=A.I. |title=Series: fundamental concepts with historical exposition |year=1967 |edition=English translation of 3rd revised edition (1961) in Russian |publisher=Hindustan Pub. Corp. |id={{LCCN|68|0|17528}}}} |
|||
*{{cite book |author=Saichev, A.I., and W.A. Woyczyński |title=Distributions in the physical and engineering sciences, Volume 1 |publisher=Birkhaüser |year=1996 |isbn= 0-8176-3924-1}} |
|||
*{{cite journal |last=Tucciarone |first=John |title=The development of the theory of summable divergent series from 1880 to 1925 |journal=Archive for History of Exact Sciences |volume=10 |issue=1-2 |year=1973 |month=January |pages=1–40 |doi=10.1007/BF00343405}} |
|||
*{{cite book |first=Anders |last=Vretblad |title=Fourier Analysis and Its Applications |year=2003 |publisher=Springer |isbn= 0387008365}} |
|||
*{{cite book |last=Weidlich |first=John E. |title=Summability methods for divergent series |year=1950 |month=June |publisher=Stanford M.S. theses|id={{OCLC|38624384}}}} |
|||
[[Kategori:Iraksak seriler]] |
|||
[[Kategori:Diziler ve seriler]] |
[[Kategori:Diziler ve seriler]] |
||
[[Kategori:Paradokslar]] |
[[Kategori:Paradokslar]] |
||
| 36. satır: | 196. satır: | ||
{{Link SM|pt}} |
{{Link SM|pt}} |
||
{{Link SM|sl}} |
{{Link SM|sl}} |
||
[[bn:১ − ২ + ৩ − ৪ + · · ·]] |
[[bn:১ − ২ + ৩ − ৪ + · · ·]] |
||
[[ca:1 − 2 + 3 − 4 + ...]] |
[[ca:1 − 2 + 3 − 4 + ...]] |
||
[[da:1 − 2 + 3 − 4 + · · ·]] |
[[da:1 − 2 + 3 − 4 + · · ·]] |
||
[[en:1 − 2 + 3 − 4 + · · ·]] |
|||
[[es:1 − 2 + 3 − 4 + · · ·]] |
[[es:1 − 2 + 3 − 4 + · · ·]] |
||
[[fa:۱ - ۲ + ۳ - ۴ +...]] |
[[fa:۱ - ۲ + ۳ - ۴ +...]] |
||
[[fi:1 − 2 + 3 − 4 + · · ·]] |
|||
[[fr:Série alternée des entiers]] |
[[fr:Série alternée des entiers]] |
||
[[it:1 − 2 + 3 − 4 + · · ·]] |
[[it:1 − 2 + 3 − 4 + · · ·]] |
||
[[ja:1-2+3-4+…]] |
|||
[[lv:1 − 2 + 3 − 4 + · · ·]] |
[[lv:1 − 2 + 3 − 4 + · · ·]] |
||
[[ja:1-2+3-4+…]] |
|||
[[no:1 − 2 + 3 − 4 + · · ·]] |
[[no:1 − 2 + 3 − 4 + · · ·]] |
||
[[pt:1 − 2 + 3 − 4 + · · ·]] |
[[pt:1 − 2 + 3 − 4 + · · ·]] |
||
[[sl:1 − 2 + 3 − 4 + · · ·]] |
[[sl:1 − 2 + 3 − 4 + · · ·]] |
||
[[fi:1 − 2 + 3 − 4 + · · ·]] |
|||
[[sv:1 − 2 + 3 − 4 + · · ·]] |
[[sv:1 − 2 + 3 − 4 + · · ·]] |
||
[[th:1 − 2 + 3 − 4 + · · ·]] |
[[th:1 − 2 + 3 − 4 + · · ·]] |
||
Sayfanın 15.19, 24 Ağustos 2009 tarihindeki hâli
Bu sayfanın ya da bir kısmının Türkçeye çevrilmesi gerekmektedir. Bu sayfanın tamamı ya da bir kısmı Türkçe dışındaki bir dilde yazılmıştır. Madde, alakalı dilin okuyucuları için oluşturulmuşsa o dildeki Vikipedi'ye aktarılmalıdır. İlgili değişiklikler gerçekleşmezse maddenin tamamının ya da çevrilmemiş kısımların silinmesi sözkonusu olabilecektir. İlgili çalışmayı yapmak üzere bu sayfadan destek alabilirsiniz |
Bu sayfada devam eden bir çalışma vardır. Yardım etmek istiyorsanız ya da çalışma yarım bırakılmışsa, çalışmayı yapan kişilerle iletişime geçebilirsiniz. Bu sayfada son yedi gün içinde değişiklik yapılmadığı takdirde şablon sayfadan kaldırılacaktır. En son değişiklik, 14 yıl önce Superyetkin (katkılar | kayıtlar) tarafından gerçekleştirildi (). |

Matematikte 1 − 2 + 3 − 4 + · · · sınırsız bir dizidir. Bu dizi art arda gelen pozitif tam sayıların verilen sırayla değişimini gösterir. Sigma toplama gösterimini kullanarak serinin ilk m teriminin toplamı şöyle ifade edilebilir:
Iraksak (kısmi toplamlar sırası 1, −1, 2, −2, · · · biçiminde süren) diziler herhangi bir sınıra yakınsamazlar. Bu, 1 − 2 + 3 − 4 + · · · dizisinin ıraksadığı biçiminde de ifade edilebilir.
Tüm bunlara karşın, Leonhard Euler 18. yüzyılın ortalarında bu dizinin mantığa aykırı görünen bir denklem olduğunu öne sürmüştür.
Bu denklemin doğru açıklaması daha sonraki yıllarda da tartışma konusu olmuştur. 1980'lerin başlarında Ernesto Cesàro, Émile Borel ve diğerleri, farklı diziyle genellenen toplamları ifade etmesi için Euler'in denemelerinin yeni yorumlarını kapsayan iyi tanımlanmış yöntemler geliştirmeye çalışmışlardır. Bu toplanabilirlik yöntemlerinin birçoğu 1 − 2 + 3 − 4 + · · · toplamının 1⁄4'e eşit olduğunu öne sürmektedir. Cesàro toplamı 1 − 2 + 3 − 4 + · · ·'e yaklaşık da olsa bir değer atayamayan az sayıdaki yöntemden biridir. Bu, Abel toplamı gibi daha sağlam sonuçlar veren yöntemlerin kullanılmasını zorunlu kılmaktadır.
1 − 2 + 3 − 4 + · · · dizisi, Grandi'nin dizisi 1 − 1 + 1 − 1 + · · · ile yakından ilintilidir.
Iraksaklık
Dizinin her bir elemanı (1, −2, 3, −4, · · ·) hem + hem de − yönde 0'dan uzaklaşmaktadır; bu yüzden 1 − 2 + 3 − 4 + · · ·, terim testi ile ayrılır. Bu yöntem, bir noktada birleşmesiyle ya da sınırsız bir dizinin ayrılmasıyla, bir sonsuz serinin ıraksaklığını belirlemenin basit bir yöntemidir. Başka bir deyişle, 1 − 2 + 3 − 4 + · · ·'ün kısmi toplamları:
- 1 = 1,
- 1 − 2 = −1,
- 1 − 2 + 3 = 2,
- 1 − 2 + 3 − 4 = −2,
- 1 − 2 + 3 − 4 + 5 = 3,
- 1 − 2 + 3 − 4 + 5 − 6 = −3,
- · · ·
biçiminde ifade edilebilir.
Heuristics for summation
Stability and linearity
Since the terms 1, −2, 3, −4, 5, −6, … follow a simple pattern, the series 1 − 2 + 3 − 4 + … can be manipulated by shifting and term-by-term addition to yield a numerical value. If it can make sense to write s = 1 − 2 + 3 − 4 + … for some ordinary number s, the following manipulations argue for s = 1⁄4:[1]

So . This derivation is depicted graphically on the right.
Although 1 − 2 + 3 − 4 + … does not have a sum in the usual sense, the equation s = 1 − 2 + 3 − 4 + … = 1⁄4 can be supported as the most natural answer if such a sum is to be defined. A generalized definition of the "sum" of a divergent series is called a summation method or summability method, which sums some subset of all possible series. There are many different methods (some of which are described below) that are characterized by the properties that they share with ordinary summation. What the above manipulations actually prove is the following: Given any summability method that is linear and stable and sums the series 1 − 2 + 3 − 4 + …, the sum it produces is 1⁄4. Furthermore, since
such a method must also sum Grandi's series as 1 − 1 + 1 − 1 + … = 1⁄2.
Cauchy product
In 1891, Ernesto Cesàro expressed hope that divergent series would be rigorously brought into calculus, pointing out, "One already writes (1 − 1 + 1 − 1 + …)2 = 1 − 2 + 3 − 4 + … and asserts that both the sides are equal to 1⁄4."[2] For Cesàro, this equation was an application of a theorem he had published the previous year, one that may be identified as the first theorem in the history of summable divergent series. The details on his summation method are below; the central idea is that 1 − 2 + 3 − 4 + … is the Cauchy product of 1 − 1 + 1 − 1 + … with 1 − 1 + 1 − 1 + ….
The Cauchy product of two infinite series is defined even when both of them are divergent. In the case where Σan = Σbn = Σ(−1)n, the terms of the Cauchy product are given by the finite diagonal sums
The product series is then
Thus a summation method that respects the Cauchy product of two series and sums 1 − 1 + 1 − 1 + … = 1⁄2, will also sum 1 − 2 + 3 − 4 + … = 1⁄4. With the result of the previous section, this implies an equivalence between summability of 1 − 1 + 1 − 1 + … and 1 − 2 + 3 − 4 + … with methods that are linear, stable, and respect the Cauchy product.
Cesàro's theorem is a subtle example. The series 1 − 1 + 1 − 1 + … is Cesàro-summable in the weakest sense, called (C, 1)-summable, while 1 − 2 + 3 − 4 + … requires a stronger form of Cesàro's theorem[3], being (C, 2)-summable. Since all forms of Cesàro's theorem are linear and stable, the values of the sums are as we have calculated.
Specific methods
Cesàro and Hölder

To find the (C, 1) Cesàro sum of 1 − 2 + 3 − 4 + …, if it exists, one needs to compute the arithmetic means of the partial sums of the series. The partial sums are
- 1, −1, 2, −2, 3, −3, …,
and the arithmetic means of these partial sums are
- 1, 0, 2⁄3, 0, 3⁄5, 0, 4⁄7, ….
This sequence of means does not converge, so 1 − 2 + 3 − 4 + … is not Cesàro summable.
There are two well-known generalizations of Cesàro summation: the conceptually simpler of these is the sequence of (H, n) methods for natural numbers n. The (H, 1) sum is Cesàro summation, and higher methods repeat the computation of means. Above, the even means converge to 1⁄2, while the odd means are all equal to 0, so the means of the means converge to the average of 0 and 1⁄2, namely 1⁄4.[4] So 1 − 2 + 3 − 4 + … is (H, 2) summable to 1⁄4.
The "H" stands for Otto Hölder, who first proved in 1882 what mathematicians now think of as the connection between Abel summation and (H, n) summation; 1 − 2 + 3 − 4 + … was his first example.[5] The fact that 1⁄4 is the (H, 2) sum of 1 − 2 + 3 − 4 + … guarantees that it is the Abel sum as well; this will also be proved directly below.
The other commonly formulated generalization of Cesàro summation is the sequence of (C, n) methods. It has been proven that (C, n) summation and (H, n) summation always give the same results, but they have different historical backgrounds. In 1887, Cesàro came close to stating the definition of (C, n) summation, but he gave only a few examples. In particular, he summed 1 − 2 + 3 − 4 + …, to 1⁄4 by a method that may be rephrased as (C, n) but was not justified as such at the time. He formally defined the (C, n) methods in 1890 in order to state his theorem that the Cauchy product of a (C, n)-summable series and a (C, m)-summable series is (C, m + n + 1)-summable.[6]
Abel summation

In a 1749 report, Leonhard Euler admits that the series diverges but prepares to sum it anyway:
…when it is said that the sum of this series 1−2+3−4+5−6 etc. is 1⁄4, that must appear paradoxical. For by adding 100 terms of this series, we get –50, however, the sum of 101 terms gives +51, which is quite different from 1⁄4 and becomes still greater when one increases the number of terms. But I have already noticed at a previous time, that it is necessary to give to the word sum a more extended meaning….[7]
Euler proposed a generalization of the word "sum" several times; see Euler on infinite series. In the case of 1 − 2 + 3 − 4 + …, his ideas are similar to what is now known as Abel summation:
…it is no more doubtful that the sum of this series 1−2+3−4+5 + etc. is 1⁄4; since it arises from the expansion of the formula 1⁄(1+1)2, whose value is incontestably 1⁄4. The idea becomes clearer by considering the general series 1 − 2x + 3x2 − 4x3 + 5x4 − 6x5 + &c. that arises while expanding the expression 1⁄(1+x)2, which this series is indeed equal to after we set x = 1.[8]
There are many ways to see that, at least for absolute values |x| < 1, Euler is right in that
One can take the Taylor expansion of the right-hand side, or apply the formal long division process for polynomials. Starting from the left-hand side, one can follow the general heuristics above and try multiplying by (1+x) twice or squaring the geometric series 1 − x + x2 − …. Euler also seems to suggest differentiating the latter series term by term.[9]
In the modern view, the series 1 − 2x + 3x2 − 4x3 + … does not define a function at x = 1, so that value cannot simply be substituted into the resulting expression. Since the function is defined for all |x| < 1, one can still take the limit as x approaches 1, and this is the definition of the Abel sum:
Euler and Borel
Euler applied another technique to the series: the Euler transform, one of his own inventions. To compute the Euler transform, one begins with the sequence of positive terms that makes up the alternating series—in this case 1, 2, 3, 4, …. The first element of this sequence is labeled a0.
Next one needs the sequence of forward differences among 1, 2, 3, 4, …; this is just 1, 1, 1, 1, …. The first element of this sequence is labeled Δa0. The Euler transform also depends on differences of differences, and higher iterations, but all the forward differences among 1, 1, 1, 1, … are 0. The Euler transform of 1 − 2 + 3 − 4 + … is then defined as
In modern terminology, one says that 1 − 2 + 3 − 4 + … is Euler summable to 1⁄4.
The Euler summability implies another kind of summability as well. Representing 1 − 2 + 3 − 4 + … as
one has the related everywhere-convergent series
The Borel sum of 1 − 2 + 3 − 4 + … is therefore[10]
Separation of scales
Saichev and Woyczyński arrive at 1 − 2 + 3 − 4 + … = 1⁄4 by applying only two physical principles: infinitesimal relaxation and separation of scales. To be precise, these principles lead them to define a broad family of "φ-summation methods", all of which sum the series to 1⁄4:
- If φ(x) is a function whose first and second derivatives are continuous and integrable over (0, ∞), such that φ(0) = 1 and the limits of φ(x) and xφ(x) at +∞ are both 0, then[11]
This result generalizes Abel summation, which is recovered by letting φ(x) = exp(−x). The general statement can be proved by pairing up the terms in the series over m and converting the expression into a Riemann integral. For the latter step, the corresponding proof for 1 − 1 + 1 − 1 + … applies the mean value theorem, but here one needs the stronger Lagrange form of Taylor's theorem.
Generalizations
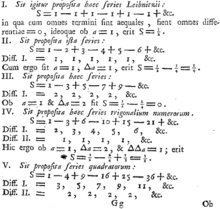
The threefold Cauchy product of 1 − 1 + 1 − 1 + … is 1 − 3 + 6 − 10 + …, the alternating series of triangular numbers; its Abel and Euler sum is 1⁄8.[12] The fourfold Cauchy product of 1 − 1 + 1 − 1 + … is 1 − 4 + 10 − 20 + …, the alternating series of tetrahedral numbers, whose Abel sum is 1⁄16.
Another generalization of 1 − 2 + 3 − 4 + … in a slightly different direction is the series 1 − 2n + 3n − 4n + … for other values of n. For positive integers n, these series have the following Abel sums:[13]
where Bn are the Bernoulli numbers. For even n, this reduces to
This last sum became an object of particular ridicule by Niels Henrik Abel in 1826:
- "Divergent series are on the whole devil's work, and it is a shame that one dares to found any proof on them. One can get out of them what one wants if one uses them, and it is they which have made so much unhappiness and so many paradoxes. Can one think of anything more appalling than to say that
- 0 = 1 − 2n + 3n − 4n + etc.
- where n is a positive number. Here's something to laugh at, friends."[14]
Cesàro's teacher, Eugène Charles Catalan, also disparaged divergent series. Under Catalan's influence, Cesàro initially referred to the "conventional formulas" for 1 − 2n + 3n − 4n + … as "absurd equalities", and in 1883 Cesàro expressed a typical view of the time that the formulas were false but still somehow formally useful. Finally, in his 1890 Sur la multiplication des séries, Cesàro took a modern approach starting from definitions.[15]
The series are also studied for non-integer values of n; these make up the Dirichlet eta function. Part of Euler's motivation for studying series related to 1 − 2 + 3 − 4 + … was the functional equation of the eta function, which leads directly to the functional equation of the Riemann zeta function. Euler had already become famous for finding the values of these functions at positive even integers (including the Basel problem), and he was attempting to find the values at the positive odd integers (including Apéry's constant) as well, a problem that remains elusive today. The eta function in particular is easier to deal with by Euler's methods because its Dirichlet series is Abel summable everywhere; the zeta function's Dirichlet series is much harder to sum where it diverges.[16] For example, the counterpart of 1 − 2 + 3 − 4 + … in the zeta function is the non-alternating series 1 + 2 + 3 + 4 + …, which has deep applications in modern physics but requires much stronger methods to sum.
Notlar
- ^ Hardy (p.6) presents this derivation in conjunction with evaluation of Grandi's series 1 − 1 + 1 − 1 + ….
- ^ Ferraro, p.130.
- ^ Hardy, p.3; Weidlich, pp.52–55.
- ^ Hardy, p.9. For the full details of the calculation, see Weidlich, pp.17–18.
- ^ Ferraro, p.118; Tucciarone, p.10. Ferraro criticizes Tucciarone's explanation (p.7) of how Hölder himself thought of the general result, but the two authors' explanations of Hölder's treatment of 1 − 2 + 3 − 4 + … are similar.
- ^ Ferraro, pp.123–128.
- ^ Euler et al., p.2. Although the paper was written in 1749, it was not published until 1768.
- ^ Euler et al., pp.3, 25.
- ^ For example, Lavine (p.23) advocates long division but does not carry it out; Vretblad (p.231) calculates the Cauchy product. Euler's advice is vague; see Euler et al., pp.3, 26. John Baez even suggests a category-theoretic method involving multiply pointed sets and the quantum harmonic oscillator. Baez, John C. Euler's Proof That 1 + 2 + 3 + … = 1/12 (PDF). math.ucr.edu (December 19, 2003). Retrieved on March 11, 2007.
- ^ Weidlich p. 59
- ^ Saichev and Woyczyński, pp.260–264.
- ^ Kline, p.313.
- ^ Knopp, p.491; there appears to be an error at this point in Hardy, p.3.
- ^ Grattan-Guinness, p.80. See Markushevich, p.48, for a different translation from the original French; the tone remains the same.
- ^ Ferraro, pp.120–128.
- ^ Euler et al., pp.20–25.
Kaynakça
- Beals, Richard (2004). Analysis: an introduction. Cambridge UP. ISBN 0-521-60047-2.
- Davis, Harry F. (May 1989). Fourier Series and Orthogonal Functions. Dover. ISBN 0-486-65973-9.
- Euler, Leonhard; Lucas Willis; and Thomas J Osler (2006). "Translation with notes of Euler's paper: Remarks on a beautiful relation between direct as well as reciprocal power series". The Euler Archive. Erişim tarihi: 2007-03-22. Originally published as Euler, Leonhard (1768). "Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques". Memoires de l'academie des sciences de Berlin. 17: 83–106.
- Ferraro, Giovanni (June 1999). "The First Modern Definition of the Sum of a Divergent Series: An Aspect of the Rise of 20th Century Mathematics". Archive for History of Exact Sciences. 54 (2): 101–135. doi:10.1007/s004070050036.
- Grattan-Guinness, Ivor (1970). The development of the foundations of mathematical analysis from Euler to Riemann. MIT Press. ISBN 0-262-07034-0.
- Hardy, G.H. (1949). Divergent Series. Clarendon Press. LCCN-91-75377.
- Kline, Morris (November 1983). "Euler and Infinite Series". Mathematics Magazine. 56 (5): 307–314.
- Lavine, Shaughan (1994). Understanding the Infinite. Harvard UP. ISBN 0674920961.
- Markushevich, A.I. (1967). Series: fundamental concepts with historical exposition (English translation of 3rd revised edition (1961) in Russian bas.). Hindustan Pub. Corp. LCCN-68-17528.
- Saichev, A.I., and W.A. Woyczyński (1996). Distributions in the physical and engineering sciences, Volume 1. Birkhaüser. ISBN 0-8176-3924-1.
- Tucciarone, John (January 1973). "The development of the theory of summable divergent series from 1880 to 1925". Archive for History of Exact Sciences. 10 (1-2): 1–40. doi:10.1007/BF00343405.
- Vretblad, Anders (2003). Fourier Analysis and Its Applications. Springer. ISBN 0387008365.
- Weidlich, John E. (June 1950). Summability methods for divergent series. Stanford M.S. theses. OCLC 38624384.
Şablon:Link SM Şablon:Link SM Şablon:Link SM Şablon:Link SM Şablon:Link SM



![{\displaystyle {\begin{array}{rclllll}4s&=&&(1-2+3-4+\cdots )&+(1-2+3-4+\cdots )&+(1-2+3-4+\cdots )&+(1-2+3-4+\cdots )\\&=&&(1-2+3-4+\cdots )&+1+(-2+3-4+5+\cdots )&+1+(-2+3-4+5+\cdots )&-1+(3-4+5-6\cdots )\\&=&1+[&(1-2-2+3)&+(-2+3+3-4)&+(3-4-4+5)&+(-4+5+5-6)+\cdots ]\\&=&1+[&0+0+0+0+\cdots ]\\4s&=&1\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7668abd7c653836f93cb4b9d00351f627da56c1a)


![{\displaystyle {\begin{array}{rcl}c_{n}&=&\displaystyle \sum _{k=0}^{n}a_{k}b_{n-k}=\sum _{k=0}^{n}(-1)^{k}(-1)^{n-k}\\[1em]&=&\displaystyle \sum _{k=0}^{n}(-1)^{n}=(-1)^{n}(n+1).\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d43c146014f7b19d308aac55a97463246ebe5c9)









