Uyumluluk (fizik)
Fizikte iki dalga kaynağı eğer sabit bir faz farkları varsa ve eşit frekansa sahip ise mükemmel bir uyuma sahiptir. Bu dalgaların sabit (zamansal ve uzaysal olarak sabit) girişime olanak veren ideal bir özelliğidir. Asla oluşmayacak durumları sınırlayan ve dalga fiziğinin anlaşılmasına yardımcı olan farklı kavramları içerir ve kuantum fiziğinde çok önemli bir konsept olmuştur. Daha genel olarak, uyumluluk tek bir dalganın veya birçok dalga içeren dalga paketlerinin fiziksel özelliklerini tanımlar.
Girişim denen olay dalga fonksiyonlarının toplamından (matematiksel açıdan) başka bir şey değildir. Tek bir dalga kendisi ile girişir, ancak bu hala iki dalganın toplamıdır (bakınız: Young's slits deneyi (en:Young's interference experiment)). Yapıcı veya yıkıcı girişimler sınır durumlardır ve iki dalga toplamın sonucu karmaşık veya kayda değer değilse bile girişim yapar.
Girişim sırasında iki dalga daha büyük genlikte bir dalga oluşturmak için bir araya gelebilir (yapıcı girişim) ya da birbirinden çıkarak ikisinden de daha küçük genlikte bir dalga meydana getirebilir (yıkıcı girişim). Eğer iki dalga sabit göreceli faza sahipse eş evreli oldukları söylenir. Eş evreliliğin miktarı giriş dalgalarıyla ilişkili girişim saçaklarının büyüklüğüne bakan girişim görünürlüğü ile kolayca ölçülebilir; uyumluluk derecesinin matematiksel kesin bir tanımı bağıntı fonksiyonları ile verilmiştir.
Uzaysal uyumluluk uzayda farklı noktalardaki dalgalar arasındaki ilişkiyi tanımlar.[1] Zamansal uyumluluk ise zamanda farklı anlarda gözlemlenen dalgalar arasındaki ilişkiyi tanımlar. İkisi de Michelson-Morley deneyi ve Young'ın girişim deneyinde gözlemlenmiştir. Michelson-Morley deneyinde aynalardan birisi kademeli olarak uzaklaştırılırken saçaklar gözlemlendiği anda demetin seyahat zamanı artar, saçaklar soluklaşır ve sonunda kaybolur; bu zamansal eş evreliliği gösterir. Buna benzer şekilde Young’ ın ikili yarık deneyinde eğer yarıklar arası mesafe artarsa uyumluluk kademeli olarak yok olur ve saçaklar görünmez olur; bu da uzaysal eş evreliliği gösterir.
Giriş[değiştir | kaynağı değiştir]
Uyumluluk ilk olarak Young'ın ikili yarık deneyi ile optik içinde düşünülmüştür ancak şu an dalgaların bulunduğu her alanda kullanılmaktadır (kustik, elektrik mühendisliği, nörobilim ve kuantum mekaniği). Uyumluluk özelliği holografi, Sagnac jiroskobu, radyo anten dizileri, optik eş evreli tomografi ve teleskop interferometreleri gibi ticari uygulamaların temelidir.
Matematiksel tanım[değiştir | kaynağı değiştir]
Kesin tanımı uyumluluğun derecesi olarak verilir.
Uyumluluk ve bağıntı[değiştir | kaynağı değiştir]
İki dalganın uyumluluğu çapraz bağıntı fonksiyonu ile miktar belirterek dalgaların ne kadar iyi bağıntılı olduklarını gösterir.[2][3][4][5][6] Çapraz bağıntı ilk dalganın evresini bildiğimizde ikinci dalganın evresini tahmin etmemizi sağlar. Örnek olarak, birbiriyle daima mükemmel bağıntılı iki dalga düşünelim. Herhangi bir zamanda faz farkı sabit olacaktır. Eğer birleştiklerinde tam bir yapıcı/yıkıcı girişim veya ikisinin arasında ancak sabit faz farkı olan bir durum oluşursa dalgaların kusursuz olarak uyumlu olduğunu söyleyebiliriz. Aşağıda da tartışılacağı üzere ikinci dalga ayrı bir varlığa sahip olmaya gerek duymaz. Farklı bir zaman veya pozisyondaki ilk dalga da olabilir. Bu durumda bağıntının ölçümü otokorelasyon fonksiyonu tarafından yapılır. Korelasyon derecesi korelasyon fonksiyonlarını içerir.[7]:545-550
Dalga benzeri durumlara örnekler[değiştir | kaynağı değiştir]
Bu durumların ortak özellikleri davranışlarının dalga eşitlikleri tarafından veya bazı genellemeler tarafından açıklanmasıdır.
- Bir halattaki dalgalar (yukarı ve aşağı)
- Bir akışkanda yüzey dalgaları
- Dönüşüm hatlarında elektromanyetik sinyaller
- Ses
- Radyo dalgaları ve mikrodalgalar
- Işık dalgaları (optik)
- Elektronlar, atomlar ve kuantum fiziği tarafından incelenen her türlü başka obje
Bu sistemlerin çoğunda dalga direkt olarak ölçülebilir. Sonuç olarak başka bir dalga ile bağıntısı kolayca hesaplanabilir. Ancak, elektrik alan tüm dedektörlerin zaman çözünürlüğünden çok daha hızlı titreşim yaptığından direkt olarak ölçülemez.[7] Bunun yerine ışığın yoğunluğunu ölçeriz. Uyumluluk içeren konseptlerin çoğu optik alanında geliştirilmiş ve diğer alanlarda kullanılmıştır. Bu nedenle uyumluluğun standart ölçümü (dalganın direkt ölçülebildiği alanlarda bile) çoğunlukla dolaylıdır.
Zamansal uyumluluk[değiştir | kaynağı değiştir]

Zamansal uyumluluk herhangi bir zaman çiftinde bir dalga ile τ kadar sonraki halinin arasındaki bağıntının ortalama değeridir. Zamansal uyumluluk bize bir kaynağın ne kadar monokromatik olduğunu söyler. Diğer bir deyişle bir dalganın kendisinin farklı zamandaki bir haliyle ne kadar iyi girişim yapabildiğini inceler. Evre veya genlik üzerindeki gecikme uyumluluk zamanı τc olarak tanımlanmıştır. τ=0 lık bir gecikmede uyumluluk derecesi mükemmeldir; gecikme τ= τc iken uyumluluk derecesi büyük ölçüde düşer. Uyumluluk uzunluğu LC dalganın τc zamanında aldığı mesafedir.[9]:560, 571-573
Uyumluluk zamanı ile sinyal süresi ; ayrıca uyumluluk uzunluğu ile uyumluluk alanı karıştırılmamalıdır.
Bant genişliği ve uyumluluk zamanı arasındaki ilişki[değiştir | kaynağı değiştir]
Büyük menzilde frekanslar içeren bir dalganın daha hızlı ilintisizleştirilebildiği gösterilebilir. Böylece burada bir takas vardır:[9]:358-359, 560:358-359, 560
- .
Usulen bu matematikteki güç spektrumunu otokorelasyon ile ilişkilendiren kıvrım teoremini takip eder.[9]:572:572
Zamansal uyumluluk örnekleri[değiştir | kaynağı değiştir]
Zamansal eşevreliliğin 4 örneği vardır.
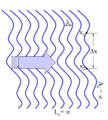
- Tek bir frekans barındıran (monokromatik) bir dalga tüm zaman gecikmelerinde kendisi ile yukardaki ilişkiyle uyumlu olarak mükemmel bağıntılıdır. (Figür 1 e bakınız)
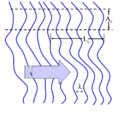
- Aksine fazı kolayca sapma yapan bir dalga kısa uyumluluk zamanına sahip olacaktır. (Figür 2 ye bakınız)
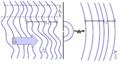
- Benzer şekilde doğal olarak geniş frekans aralığına sahip olan dalga titreşimleri de genlik hızlı değiştiğinden kısa uyumluluk zamanına sahiptir. (Figür 3 e bakınız)
- Son olarak çok geniş frekans aralığına sahip olan beyaz ışık genliği ve fazı hızlı değişen bir dalgadır. Bundan dolayı çok kısa (10 periyot civarı) uyumluluk zamanı olan beyaz ışık tutarsız/eş evresiz olarak değerlendirilir.
Monokromatik kaynaklar genellikle lazerlerdir: Böyle yüksek monokromatiklik uzun uyumluluk mesafesi anlamına gelir (100'lerce metreye kadar). Örneğin, sabit ve tek modlu helyum-neon lazeri kolayca 300 m.[10] uyumluluk mesafesine sahip ışık üretebilir. Tüm lazerler monokromatik değildir, ancak (örneğin kilitli modlu bir Ti-sapphire lazer için, Δλ = 2 nm 70 nm). LEDler Δλ = 50 nm, tarafından tanımlanır ve tungsten filaman ışıkları Δλ = 600 nm görünür; yani bu kaynaklar en monokromatik lazerlerden kat kat fazla kısa eş evreliliğe sahiptir.
Holografi uzun uyumluluk zamanlı ışık gerektirir. Buna zıt olarak optik uyumluluk tomografisi kısa uyumluluk zamanlı ışık kulllanır.
Zamansal uyumluluğun ölçümü[değiştir | kaynağı değiştir]


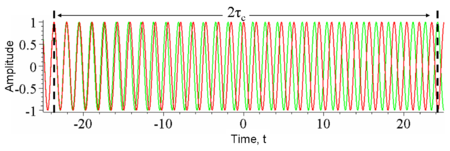
Optikte, zamansal uyumluluk Michelson veya March-Zender interferometreleri gibi interferometrelerde ölçülür. Bu cihazlarda bir dalga τ kadar gecikmeli bir kopyası ile birleştirilir. Bir dedektör interferometreden çıkan ışık yoğunluğunun zamana göre ortalamasını ölçer. Sonuçtaki girişim görünürlüğü (Figür 4 e bakınız) τ gecikmesindeki zamansal eşevreliliği verir. Doğal ışık kaynaklarının ekserisi için uyumluluk zamanı dedektörğn zaman çözünürlüğünden çok kısa olduğu için dedektör kendi kendine zaman ortalaması alır. Firgür 3 te verilen örnekleri düşünün . Sabir bir gecikmede (burada 2 τc) ; τc ye eşit t zamanına kadar büyük ölçüde dalgalanma yapacak olan yoğunluğu sonsuz hızda bir dedektör ölçebilir.
Uzaysal uyumluluk[değiştir | kaynağı değiştir]
Su dalgaları veya optik gibi bazı sistemlerde dalga benzeri durumlar bir veya iki boyutta uzanabilir. Uzaysal uyumluluk uzaydaki iki nokta x1 ve x2, nin (girişim yapacak bir dalga kapsamında) zaman ortalaması alındığında gücünü tanımlar. Daha açık olarak uzaysal uyumluluk bir dalga içindeki iki noktanın tüm zamanlar için çapraz bağıntısıdır. Eğer bir dalga sonsuz bir uzunluk boyunca yalnızca bir genlik değerine sahipse uzaysal eşevreliliği mükemmeldir. Büyük bir girişimin olduğu iki nokta arası uzaklık menzili uyumluluk alanı Ac olarak adlandırılır. Bu eşevreliliğin Young çift yarık interferometresi ile ilgili çeşididir. Ayrıca optik görüntüleme sistemlerinde ve özel olarak çeşitli türde astronomi teleskoplarında kullanılır. Bazen insanlar “uzaysak eşevreliliği” dalga benzeri bir yapının uzaysal olarak taşınmış kendi kopyası ile birleşimini ifade etmek için kullanabilmektedir.
Uzaysal uyumluluk örnekleri[değiştir | kaynağı değiştir]
- Mekansal uyumluluk
-
Figür 5: Sonsuz uyumluluk uzunluğuna sahip bir düzlem dalgası.
-
Figür 6: Değişken profilli ve sonsuz uyumluluk uzunluğuna sahip bir dalga.
-
Figür 7: Değişken profilli ve sonlu uyumluluk uzunluğuna sahip bir dalga.
-
Figür 8: Bir deliğe yaklaşan sonlu uyumluluk alanına sahip bir dalga. Dalga deliğin dışına doğru yayılacaktır. Delikten uzaklaştıkça oluşan küresel dalgalar neredeyse düz bir hal alır. Şimdi uyumluluk uzunluğu değişmediğinde uyumluluk alanı sonsuz olacaktır.
-
Figür 9: Uzaysal olarak kaymış kopyası ile birleştirilmiş sonsuz uyumluluk alanına sahip bir dalga. Girişimin bazı kısımları yapıcı bazı kısımları ise yıkıcıdır. Bu kısımların ortalaması alınarak, D uzunluğundaki bir dedektör indirgenmiş girişim görünürlüğünü ölçecektir. Örneğin March-Zehnder interferometresi bunu yapacaktır.
Tungsten bir ampul filamanını düşünelim. Filaman içinde farklı noktalar bağımsız olarak ışık yayar ve sabit faz ilişkileri yoktur. Detaylı olarak, herhangi bir zamanda yayılan ışığın profili bozulmuş olacaktır. Profil uyumluluk zamanı boyunca rastgele değişecektir. Ampul gibi bir beyaz ışık kaynağında küçük olacağından filaman uzaysal olarak eşevresiz bir kaynak olarak değerlendirilir. Bunun aksine bir radyo anten dizisi büyük uzaysal eşevreliliğe sahiptir çünkü zıt uçlardaki antenler sabit faz ilişkisi içinde yayım yapar. Bir lazer tarafından üretilen ışık dalgaları sıklıkla yüksek zamansal ve uzaysal eşevreliliğe sahip olur. Lazer demetlerinin uzaysal eşevreliliği ayrıca kendini nokta modelleri olarak gösterir ve gölgenin kenarlarında kırınım saçakları görünür.
Holografi zamansal ve uzaysal açıdan eşevreli ışık gerektirir. Mucidi Dennis Gabor lazerlerin icadından on yıldan fazla süre önce başarılı hologramlar üretmiştir. Uyumlu ışık üretmek için bir cıva-buhar lambasının emisyon doğrusundan gelen monokromatik ışığı bir iğne deliği uzaysal filtresinden geçirmiştir.
Şubat 2011’de mutlak sıfır/ Bose-Einstein yoğun durumu yakınlarına kadar soğutulan helyum atomlarının akabildiği ve lazerlerde oluşan uyumlu demetler gibi davranabildiği rapor edilmiştir.[11][12]
Spektral uyumluluk[değiştir | kaynağı değiştir]
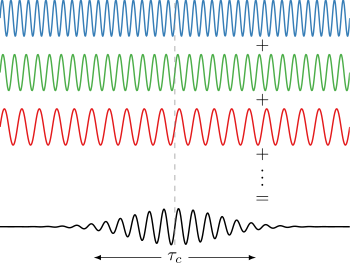
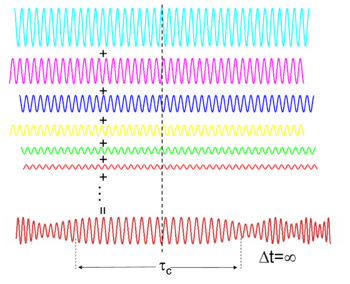
Farklı frekanslardaki dalgalar (ışıkta bunlar farklı renklerdir) eğer sabit göreceli faz ilişkileri varsa bir titreşim oluşturmak için girişim yapabilir (Fourier dönüşümüne bakınız). Diğer yandan farklı frekanstaki dalgalar eşevreli değilse, birleştirildiklerinde zamanda sürekli bir dalga(örneğin beyaz ışık veya beyaz ses) oluştururlar. Titreşimin zaman aralığı ışığın spektral bant genişliği tarafından şu şekilde sınırlandırılmıştır:
- ,
Fourier Dönüşümünün özelliklerini takip eder ve Küpfmüller belirsizlik ilkesine (quantum parçacıkları için ayrıca Heisenberg belirsizlik ilkesine sonuç verir)sonuç verir.
Eğer faz lineer olarak frekansa bağlıysa () titreşim bantgenişliği için minimum zaman aralığına sahip olacaktır.
Spektral uyumluluğun ölçümü[değiştir | kaynağı değiştir]
Spektral eşevreliliğin ölçümü yoğunluk optik korelatörü, frekans çözümlü optik sinyal ayırıcı (FROG) veya direkt elektrik alan inşası için spektral faz interferometresi gibi doğrusal olmayan optik interferometre gerektirir.
Polarizasyon ve uyumluluk[değiştir | kaynağı değiştir]
Işık elektrik alanın salınım yaptığı yönde bir polarizasyona sahiptir. Polarize olmamış ışık eşevreli olmayan ve rastgele polarizasyon açıları olan ışık dalgalarından oluşur. Polarize olmayan ışığın elektrik alanı her yönde gezinir ve iki ışık dalgası arası uyumluluk zamanı boyunca değişir. Herhangi bir açıda dönmüş emici bir kutuplaştırıcı (polarizer) zamana göre ortalama alındığında daima gelen yoğunluğun yarısını iletir.
Eğer elektrik alan küçük ölçekte bir ışık boyunca gezinirse kısmi olarak kutuplaşma meydana gelecektir böylelikle kutuplaştırıcı yoğunluğun yarısından fazla iletim yapacaktır. Eğer bir dalga kendisinin dikey olarak polarize edilmiş ve uyumluluk zamanından az bir gecikmesi olan kopyası ile birleştirilirse kısmi polarize olmuş ışık oluşturulur.
Işık demetinin polarizasyonu Poincare küresinde bir vektör ile gösterilir. Polarize olmamış ışık için vektörün değeri sıfırken polarize olmuş ışık için vektörün sonu kürenin yüzeyi üzerindedir. Kısmi olarak polarize olmuş ışığın vektörü kürenin içinde bulunur.
Uygulamalar[değiştir | kaynağı değiştir]
Holografi[değiştir | kaynağı değiştir]
Optik dalga alanlarının eşevreli toplamları holografiyi içerir. Hologafik objeler günlük hayatta banka defterleri ve kredi kartlarında yaygın olarak kullanılır.
Optik olmayan dalga alanları[değiştir | kaynağı değiştir]
Optik olmayan dalga alanlarında uyumluluk toplamı ile ilgili ileri uygulamalardır. Örneğin kuantum mekaniğinde dalga fonksiyonu e bağlı (tercüme: olası genliğin şiddeti) bir olasılık alanı düşünelim. Burada uygulamalar kuantum hesaplamanın gelecek teknolojileri ve halihazırda mümkün olan kuantum kriptografiyi ilgilendirir. Ek olarak takip eden alt konunun da problemleri ile ilgilenir.
Kuantum uyumluluğu[değiştir | kaynağı değiştir]
Kuantum mekaniğinde tüm objeler dalga benzeri özelliklere sahiptir. Örneğin Young cift yarık deneyinde elektronlar ışık dalgaları yerine kullanılabilir. Her elektronun dalga fonksiyonu iki delikten de geçer ve böylece ekran üzerindeki yoğunluk modeline iki ayrı bmlünmüş demet katılır. Standart dalga teorisine göre (Fresnel, Huygens) bu iki katılım yapıcı girişimden kaynaklı olarak aydınlık bantın yoğunluk modelinde artış sağlar (yıkıcı girişimden kaynaklı karanlık bantta olan ile birbirine geçmeli). (Her bölünmüş demet kendi kendine karanlık bantta daha az aydınlık bantta daha çok görünen bir kırınım modeli üretir.) Bu girişim ve kırınım yeteneği (klasik veya kuantum) dalganın eşevreliliği ile ilgilidir. Elektronun dalga ile yer değiştirmesi kuantum teorisine özel bir durumdur.
Gelen demet kuantum saf durumunda gösterildiğinde iki yarığın akıntı yönündeki bölünmüş demetler saf durumların bir toplamı olarak gösterilir. (Bu iki parçacık veya dolaşık durum ile ilgili Bell eşitlikleri: iki 1- cisim durumunun bir çeşit eşevreliliği olan 2 -cisim durumu, ile yapılamaz.). Mükemmel derecede eşevreli olmayan yolların kuantum tanımı karışık durumdur. Mükemmel eşevreli bir durum saf eşevreli durum üzerine bir yoğunluk matrisine sahipken karışık durum karışımı oluşturan saf durumların klasik olasılıksal dağılımı ile tanımlanmıştır.
Makroskopik boyutta kuantum eşevrelliği yeni bir olguya yol açar: sözde makroskobik kuantum olgusu. Örneğin lazer, süperiletkenlik ve süperakışkanlık etkileri makroskopik boyutta belirgin olan yüksek derecede eşevreli kuantum sistemi örnekleridir. Süperakışkanlık ve lazer ışığı için makroskopik kuantum eşevreliliği birinci dereceden (1-cisim) eşevreliliği ile ilgiliyken süperiletkenlik ikinci dereceden uyumluluk ile ilgilidir. (Elektronlar gibi fermiyonlar için yalnızca çift dereceden uyumluluk mümkündür.) Sıvı helyum-4 teki süperakışkanlık kısmi Bose-Einstein yoğuşması ile ilgilidir. Burada yoğun kısım tek parçacık durumu ile tanımlanır. [örneğin, F. W. Cummings & J. R. Johnston, Fiz. Rev. 151 (1966); Bulma 164, 270 (1967)]
Kuantum eşevreliliğin makroskopik boyutta oluşması ile ilgili olarak klasik elektromanyetik alanın makroskopik kuantum uyumlulukte görünmesi ilgi çekicidir. En açık örnek radyo ve TV için sinyal taşıyıcılarıdır. Onlar uyumluluk için Glauber kuantum tanımını sağlarlar.
Ayrıca bakınız[değiştir | kaynağı değiştir]
Kaynakça[değiştir | kaynağı değiştir]
- ^ Hecht (1998). Optics (3. bas.). Addison Wesley Longman. ss. 554-574. ISBN 0-201-83887-7.
- ^ Rolf G. Winter; Aephraim M. Steinberg (2008). "Coherence". AccessScience. McGraw-Hill. 6 Mart 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 21 Mayıs 2016.
- ^ M.Born; E. Wolf (1999). Principles of Optics (7. bas.). Cambridge University Press. ISBN 978-0-521-64222-4.
- ^ Loudon, Rodney (2000). The Quantum Theory of Light. Oxford University Press. ISBN 0-19-850177-3.
- ^ Leonard Mandel; Emil Wolf (1995). Optical Coherence and Quantum Optics. Cambridge University Press. ISBN 0-521-41711-2.
- ^ Arvind Marathay (1982). Elements of Optical Coherence Theory. John Wiley & Sons. ISBN 0-471-56789-2.
- ^ Peng, J.-L.; Liu, T.-A.; Shu, R.-H. (2008). "Optical frequency counter based on two mode-locked fiber laser combs". Applied Physics B. 92 (4). s. 513. Bibcode:2008ApPhB..92..513P. doi:10.1007/s00340-008-3111-6.
- ^ Christopher Gerry; Peter Knight (2005). Introductory Quantum Optics. Cambridge University Press. ISBN 978-0-521-52735-4.
- ^ a b c Hecht, Eugene (2002), Optics (İngilizce) (4. bas.), United States of America: Addison Wesley, ISBN 0-8053-8566-5
- ^ Saleh, Teich. Fundamentals of Photonics. Wiley.
- ^ Hodgman, S. S.; Dall, R. G.; Manning, A. G.; Baldwin, K. G. H.; Truscott, A. G. (2011). "Direct Measurement of Long-Range Third-Order Coherence in Bose-Einstein Condensates". Science. 331 (6020). ss. 1046-1049. Bibcode:2011Sci...331.1046H. doi:10.1126/science.1198481. PMID 21350171.
- ^ Pincock, S. (25 Şubat 2011). "Cool laser makes atoms march in time". ABC Science. ABC News Online. 28 Ağustos 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 2 Mart 2011.
Dış bağlantılar[değiştir | kaynağı değiştir]
- "Dr. SkySkull". "Optik temelleri: Tutarlılık" 15 Mart 2016 tarihinde Wayback Machine sitesinde arşivlendi.. Kafatası Yıldız.