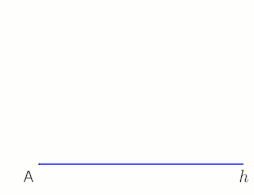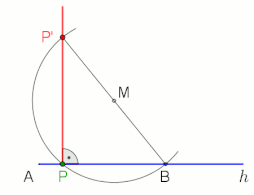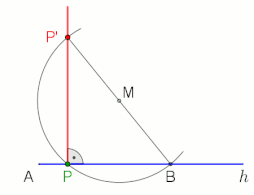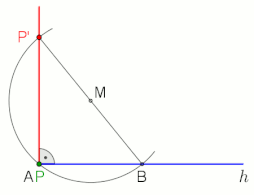
Dik açı
| Açı türleri |
|---|
| 2B açılar |
| 2B açı çiftleri |
| 3B açılar |


Geometri ve trigonometride, bir dik açı,[1] bir çeyrek dönüşe[2] tam olarak 90° (derece) bir açıdır.[3] Bir ışın, uç noktası bir doğru üzerinde olacak şekilde yerleştirilirse ve bitişik açılar eşitse, o zaman bunlar dik açılardır.[4] Terim, Latince angulus rectus’tan öykünmedir; burada rectus, yatay bir taban çizgisine düşey olan dikey manasında "dik (direk)" anlamına gelir.
Dik açı modern mimaride en çok kullanılan açıdır.[kaynak belirtilmeli]
Yakından ilgili ve önemli geometrik kavramlar dik kesişim alanına ve dik açı oluşturacak doğruları, yani doğru diklik (ortagonal) genellikle vektörlere uygulanan dik açı oluşturan bir özelliktir. Bir üçgende dik açının varlığı, dik üçgenler[5] için belirleyici faktördür, bu da dik açıyı trigonometri için temel yapar.
Etimoloji[değiştir | kaynağı değiştir]
"Dik açı"daki "dik" kelimesinin anlamı, muhtemelen dikili (erect), düz (straight), dikey (upright) veya dik (perpendicular) olarak tercüme edilebilen latin sıfat rectusa atıfta bulunur. Bir Yunan eşdeğer, düz (straight) ya da dik (perpendicular) anlamına gelen orthos (bakınız diklik, ortogonal)'dur.
Temel geometride[değiştir | kaynağı değiştir]
Bir dikdörtgen, dört dik açıya sahip bir dörtgendir. Bir kare, eşit uzunluktaki kenarlara ek olarak dört dik açıya sahiptir.
Pisagor teoremi, bir üçgenin ne zaman dik üçgen olduğunun nasıl belirleneceğini ifade eder.
Semboller[değiştir | kaynağı değiştir]

Unicode'da, bir dik açı için sembol, U+221F ∟ RIGHT ANGLE (HTML ∟⧼dot-separator⧽ )'dir. Benzer şekle sahip olan U+231E ⌞ BOTTOM LEFT CORNER (HTML ⌞⧼dot-separator⧽ ) sembolu ile karıştırılmamalıdır. İlişkili semboller U+22BE ⊾ RIGHT ANGLE WITH ARC (HTML ⊾⧼dot-separator⧽ ), U+299C ⦜ RIGHT ANGLE VARIANT WITH SQUARE (HTML ⦜⧼dot-separator⧽ ), and U+299D ⦝ MEASURED RIGHT ANGLE WITH DOT (HTML ⦝⧼dot-separator⧽ )'dir.[6]
Diyagramlarda, bir açının dik açı olduğu gerçeği, bir dik üçgenin diyagramında görüldüğü gibi, genellikle diyagramdaki açıyla bir kare oluşturan sağa doğru küçük bir dik açı eklenerek ifade edilir (İngiliz İngilizcesinde, dik açılı üçgen). Ölçülen açı sembolü, noktalı bir yay, Almanca konuşulan ülkeler ve Polonya dahil olmak üzere bazı Avrupa ülkelerinde dik açı için alternatif bir sembol olarak kullanılır.[7]
Öklid[değiştir | kaynağı değiştir]
Öklid'in Elementlerinde dik açılar temeldir. Dik doğruları da tanımlayan Kitap 1, tanım 10'da tanımlanmıştır. Tanım 10, sayısal derece ölçümlerini kullanmaz, bunun yerine dik açının ne olduğunun tam kalbine, yani iki eşit ve bitişik açı oluşturmak için kesişen iki düz çizgiye dokunur.[8] Dik açı oluşturan düz doğrulara dik denir.[8] Öklid, keskin açıları (dik açıdan küçük olanlar) ve geniş açıları (dik açıdan büyük olanlar) tanımlamak için 11 ve 12 numaralı tanımlarda dik açıları kullanır.[8] Toplamları dik açı ise iki açı, tamamlayıcı olarak adlandırılır.[9]
Kitap 1 Önerme 4, tüm dik açıların eşit olduğunu belirtir, bu da Öklid'in diğer açıları ölçmek için bir birim olarak dik açıyı kullanmasına izin verir. Öklid'in yorumcusu Proclus, önceki önermeleri kullanarak bu önermenin bir ispatını verdi, ancak bu ispatın bazı gizli varsayımları kullandığı tartışılabilir. Saccheri de bir kanıt verdi, ancak daha açık bir varsayım kullanıyordu. Hilbert'in geometri aksiyomatizasyonunda bu ifade bir teorem olarak verilir, ancak çok fazla temel çalışmadan sonra verilir. Öklid'in malzemesini sunma sırasına göre, 4 numaralı önerme öncekilerden ispatlanabilse bile, bunu dahil etmenin gerekli olduğu ileri sürülebilir, çünkü o olmadan, dik açıyı bir ölçü birimi olarak kullanan 5. önerme, hiçbir anlam ifade etmez.[10]
Diğer birimlere dönüştürme[değiştir | kaynağı değiştir]
Bir dik açı farklı birimlerle ifade edilebilir:
- 14 dönüş (devir)
- 90° (derece)
- π2 radyan veya τ4 rad
- 100 grad (grade, gradian veya gon olarak da adlandırılır)
- 8 nokta (32 noktalı pusula gülünden)
- 6 saat (astronomik saat açısı)
3-4-5 kuralı[değiştir | kaynağı değiştir]
Tarih boyunca, marangozlar ve duvarcılar bir açının gerçek bir "dik açı" olup olmadığını doğrulamanın hızlı bir yolunu biliyorlardı. Bu, en çok bilinen Pisagor üçlüsü (3, 4, 5)'e dayanır ve "3-4-5 kuralı" olarak adlandırılır. Söz konusu açıdan, bir taraf boyunca tam olarak 3 birim uzunluğunda ve ikinci taraf boyunca tam olarak 4 birim uzunluğunda düz bir çizgi geçmek, bir hipotenüs (ölçülen iki uç noktayı birleştiren dik açının karşısındaki daha uzun çizgi) tam olarak 5 birim uzunluğundadır. Bu ölçüm hızlı ve teknik aletler olmadan yapılabilir. Ölçümün arkasındaki geometrik yasa Pisagor teoremidir ("Bir dik üçgenin hipotenüsünün karesi, bitişik iki kenarın karelerinin toplamına eşittir").
Thales teoremi[değiştir | kaynağı değiştir]
Thales teoremi, bir yarım çember içine çizilmiş bir açının (yarım çember üzerinde bir tepe noktası ve yarım çemberin uç noktalarından geçen tanımlayıcı ışınları ile) bir dik açı olduğunu belirtir.
Dik açı ve Thales teoreminin dahil edildiği iki uygulama örneği için animasyonlara bakınız.
Ayrıca bakınız[değiştir | kaynağı değiştir]
| Wikimedia Commons'ta Dik açı ile ilgili ortam dosyaları bulunmaktadır. |
- Kartezyen koordinat sistemi
- Ortogonalite (Diklik)
- Dik
- Dikdörtgen
- Açı türleri
- Geometri
- Trigonometri
- Üçgen
- Dörtgen
- Kesir
Notlar[değiştir | kaynağı değiştir]
- ^ Dikaçı şeklinde bileşik olarak da yazılır. Bkz. "Türkçe Sözlük". Dil Derneği. 16 Mart 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Ağustos 2011.
- ^ "Right Angle". Math Open Reference. 30 Ekim 2006 tarihinde kaynağından arşivlendi. Erişim tarihi: 26 Nisan 2017.
- ^ Wentworth s. 11
- ^ Wentworth s. 8
- ^ Wentworth s. 40
- ^ Unicode 5.2 Karakter Kodu Çizelgeleri Matematiksel Operatörler 12 Haziran 2018 tarihinde Wayback Machine sitesinde arşivlendi., Çeşitli Matematiksel Semboller-B 12 Kasım 2018 tarihinde Wayback Machine sitesinde arşivlendi.
- ^ Susanne Müller-Philipp & Hans-Joachim Gorski (2011). Leitfaden Geometrie [Geometry Handbook] (Almanca). Springer. ISBN 9783834886163. 9 Ocak 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 8 Nisan 2021.
- ^ a b c Heath s. 181
- ^ Wentworth s. 9
- ^ Paragraf için bkz. Heath ss. 200-201
Kaynakça[değiştir | kaynağı değiştir]
- Wentworth, G.A. (1895). A Text-Book of Geometry. Ginn & Co.
- Euclid (1908), Elements Vol. 1, T. L. Heath (commentary and trans.) tarafından çevrildi, Cambridge, 20 Ocak 2021 tarihinde kaynağından arşivlendi, erişim tarihi: 8 Nisan 2021