Çizge teorisi

Graf teorisi, çizge teorisi veya çizit teorisi (İngilizce: graph theory), grafları inceleyen matematik dalıdır. Graf, düğümler ve bu düğümleri birbirine bağlayan kenarlardan oluşan bir tür ağ yapısıdır. Bir graf, çizge veya çizit, düğümlerden (köşeler) ve bu düğümleri birbirine bağlayan kenarlardan (yaylardan, bağıntılardan) oluşur.
Temeli 1736'da Leonhard Euler tarafından atılmıştır.[1]
Graf teorisi üzerinde yapılan çalışmalar, Petri ağları gibi birçok yeni kavramın geliştirilmesine imkân sağlamıştır.
Teorinin tarihi[değiştir | kaynağı değiştir]
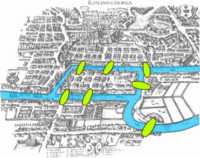
Leonhard Euler tarafından, 1736 yılında, Königsberg'in yedi köprüsü (Almanca: Die Sieben Brücken von Königsberg) adında günümüzde hâlâ popülerliğini koruyan bir problem ile ilgili olarak yazılan bir makale, graf teorisinin kesin başlangıç tarihidir.
Matematiksel tanımı[değiştir | kaynağı değiştir]

Bir G grafı iki küme ile ifade edilir: G = (D, K). Bu ifadede D düğümler kümesi, K ise (düğümler ile ilişkili) kenarlar kümesi olarak ifade edilir.
- Eğer düğümleri birbirine bağlayan kenarlar için giriş ve çıkış yönleri belirli ise bu kenarlara yönlü kenarlar denir.
- Eğer bir düğümden çıkan ve yine aynı düğüme giren bir kenar varsa (mesela A'dan çıkıp A'ya yeniden giren bir kenar), bu bir döngü (İngilizce: loop) olarak ifade edilir.
- Eğer bir düğümden bir başka düğüme giden aynı yöne sahip veya yönsüz iki adet kenar varsa bu kenarlara paralel kenarlar denir.
Sağdaki yönsüz, örnek graf için küme gösterimi aşağıdaki şekilde yapılır.
D = {A, B, C, D}
K = {(A, D), (D, A), (A, B), (A, C), (C, B), (C, D)}
G = (D, K)
Bu örnekte A ve D düğümleri iki adet paralel kenar içerir.
Graf tipleri[değiştir | kaynağı değiştir]
| Graf tipi | Kenar tipi | Çoklu kenara izin | Döngüye izin? |
|---|---|---|---|
| Basit graf | Yönsüz | Hayır | Hayır |
| Çoklu graf | Yönsüz | Evet | Hayır |
| Pseudo (sahte) graf | Yönsüz | Evet | Evet |
| Yönlü graf | Yönlü | Hayır | Evet |
| Yönlü çoklu graf | Yönlü | Evet | Evet |
Tanımlar ve örnekler[değiştir | kaynağı değiştir]
Yol haritasıyla haritada belirtilen yollarla bir beldeden diğer bir beldeye nasıl gidileceğine karar verilir. Sonuç olarak bu durumda nesnelerin iki farklı kümesi ile ilgilenilmektedir: Beldeler ve yollar. Daha önce gördüğümüz gibi böyle nesnelerin kümeleri bir bağıntı tanımlamak için kullanılabilir. Eğer V kümesi ile beldeler kümesini ve E kümesi ile de yollar kümesini gösterirsek, V kümesi üzerinde yalnız E'deki yolları kullanarak a beldesinden (noktasından) b noktasına seyahat edilebiliyorsa aβb yazarak, bir β bağıntısı tanımlanabilir. Eğer E'deki yollar gidiş-geliş yolları ise bβa da gerçeklenir. Eğer inceleme altındaki bütün yollar gidiş-gelişli yollar ise bu bağıntı simetriktir. Bir bağıntıyı tanımlamanın bir yolu, onun elemanlarını sıralı çiftler olarak listeleyerek vermektir. Bunun, aşağıdaki şekilde gösterildiği gibi çizgiler kullanarak yapılması daha uygundur.
Ayrıca bakınız[değiştir | kaynağı değiştir]
Kaynakça[değiştir | kaynağı değiştir]
- ^ (İngilizce) Biggs, N.; Lloyd, E. and Wilson, R. (1986), Graph Theory, 1736-1936, Oxford University Press.
Dış bağlantılar[değiştir | kaynağı değiştir]
| Matematik ile ilgili bu madde taslak seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |

