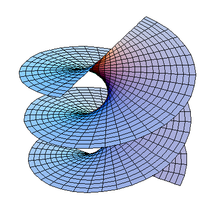
Helikoid

α = 1, −1 ≤ ρ ≤ 1 and −π ≤ θ ≤ π değerleriyle bir helikoid.

$0\leq r\leq r_{0},0\leq \phi \leq \phi _{0}$ helisel bir yüzeyin kesiti

Düzlem ve katenoidden sonra helis yüzey de denen helikoid bilinen üçüncü minimal yüzeydir. Helikoid, helis ve eksenle tanımlanan yüzeydir.

Mathematica kullanılarak çizilmiş bir helikoid.

Helis ve eksenindeki sabun film tabakasıyla oluşan bir helikoid.

Tarihçe

Helikoid, 1774'te Euler ve 1776'da Jean Baptiste Meusnier tarafından tanımlanmıştır.

Catalan 1842'de bunun düzlem dışında tek minimal çizgili yüzey olduğunu kanıtlamıştır.

Meeks ve Rosenberg 2005 yılında (Colding-Minicozzi eşitsizliklerine dayanarak) basit bağlantılı minimal yüzeylerin yalnızca iki tipinin bulunduğunu kanıtladılar, $\mathbb {R} ^{3}$'de yalnızca 2 tür basit bağlantılı minimal yüzey vardır: düzlem ve helikoidler.

1990'larda David Allen Hoffman ve meslektaşları helikoidden kaynaklı, sıfırdan farklı topolojik ailenin başka örneklerini buldular. Cins 1 için tam gömülebilir minimal yüzey oluşturduklarının kanıtı 2009'da Hoffman, Michael Wolf ve Matthias Weber tarafından sağlandı. (Bundan önce aile 0 durumu hariç, bu yalnızca sonsuz aile durumu için kanıtlanıyordu).

Tanım

Adı, helis ile benzerliğinden türetilmiştir: Helikoid üzerindeki her nokta için helikoidin içerdiği ve o noktadan geçen bir helis vardır. Düzlemsel aralığın negatif ve pozitif sonsuza kadar uzandığı düşünüldüğünden, yakın gözlem iki paralel veya ayna düzleminin görünümünü gösterir, gerçekte ortak düzlem aynı zamanda zıt perspektiften de izlense bile ortak düzlemin atlandığı görülebilir.

Helikoid aynı zamanda çizgili bir yüzeydir (ve dik konoiddir). Alternatif olarak yüzeydeki herhangi bir nokta için yüzeyde oradan geçen bir çizgi vardır. Helikoid aynı zamanda diferansiyel geometri anlamında bir öteleme yüzeyidir.

Helikoid Arşimet vidası şeklindedir ancak her yönde sonsuz şekilde uzanır.

Helikoid Kartezyen koordinatlar'da aşağıdaki parametrik denklem’lerle açıklanabilir:

$x=\rho \cos(\alpha \theta ),\$$y=\rho \sin(\alpha \theta ),\$$z=\theta ,\$

burada ρ ve θ negatif sonsuz’dan pozitif sonsuza kadar değişirken α bir sabittir.

Eğer α pozitifse helikoid şekilde gösterildiği gibi sağa doğru, negatifse sola doğru döner.

Helikoidin temel eğrilikleri $\pm \alpha /(1+\alpha ^{2}\rho ^{2})\$'dir. Bu, miktarların toplamı ortalama eğriliği verir (helikoid minimal yüzey olduğundan sıfırdır) ve çarpım Gauss eğriliğini verir.

Helikoid, $\mathbb {R} ^{2}$ düzlemine göre homeomorfik'tir. Bunu görmek için α'nın verilen değerinden sıfıra kadar sürekli olarak azalmasına izin verilir. α'nın her ara değeri, α = 0'a ulaşılana ve helikoid dikey bir düzlem haline gelene kadar farklı bir helikoidi tanımlar. Aksi durumda, düzlemde bir çizgi veya "eksen" seçilerek ve ardından düzlem bu eksen etrafında döndürülerek bir düzlem helikoide dönüştürülebilir.

Yarıçapı R olan bir helikoid h yüksekliği kadar yükselirken kendi ekseni etrafında θ açısı kadar dönüyorsa, yüzey alanı şu denklemle verilir.

${\frac {\theta }{2}}\left[R{\sqrt {R^{2}+c^{2}}}+c^{2}\ln \left({\frac {R+{\sqrt {R^{2}+c^{2}}}}{c}}\right)\right],\ c={\frac {h}{\theta }}.$

Helikoid ve katenoid

Helikoidin katenoide dönüşümünü gösteren animasyon.

Helikoid ve katenoit yerel olarak izometrik yüzeylerdir.

Minimal alan

$r,\phi$ parametrelerine karşılık gelen noktadaki sarmal yüzeyin ana eğrilikleri şu şekildedir:

${\frac {1}{1+r^{2}}}$ ve $-{\frac {1}{1+r^{2}}}$, ortalama eğrilik her noktada sıfırdır, sarmal yüzey bir minimal yüzeydir.

Topolojik düzleme göre homeomorfik'tir.

Yerel olarak katenoid ile helikoid izometriktir ancak homeomorfik değildir. Helikoid ve katenoid, helikoid-katenoid minimal yüzey ailesinin parçalarıdır.

Helikoid çizgili bir yüzey ve vida yüzeyidir. Aynı zamanda kayan yüzey olarak da temsil edilebilir.

Pratik ve Bilimsel Önemi

• 
  Kimya: (P)-(+)-Heptahelisen saat yönünde sarmallık içerir.
• 
  Kimya: (M)-(–)-Heptahelisen saat yönünün tersine sarmallık sergiler.
• 
  Karşılaştırma amacıyla Roma'daki Vatikan Müzesi'ndeki sarmal merdiven sarmal yapı örneğidir. Simetri (P)-heptahelisen simetrisine karşılık gelir
• 
  Bu sarmaşığın vida dönüşü (M)-heptahelisen'in dönüş yönüne karşılık gelir

Helisel yüzeylerin doğada, mimaride ve kimyada çok sayıda uygulama alanı vardır. Dönme yönünde rol oynarlar.

Ayrıca bakınız

• Dini yüzeyi
• Yüzeyler listesi
• Sarmal

• 
  Silikon bir nesnenin bükülmesiyle helikoidlerin oluşumu.

Dış bağlantılar

• Hazewinkel, Michiel, (Ed.) (2001), "Helicoid", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104 
• WebGL-based Interactive 3D Helicoid