Fuhrmann çemberi
Görünüm
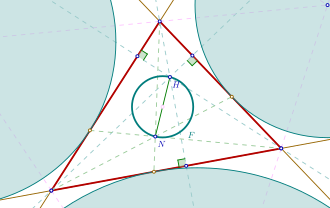
Fuhrmann çemberi

Geometride, adını Alman matematikçi Wilhelm Fuhrmann (1833-1904)'dan alan bir üçgenin Fuhrmann çemberi, çap olarak ortosentr ile Nagel noktası arasındaki doğru parçasına sahip çemberdir. Bu çember, Fuhrmann üçgeninin çevrel çemberi ile aynıdır.[1]
Kenarları a, b ve c ve çevrel çemberinin yarıçapı R olan bir üçgenin Fuhrmann çemberinin yarıçapı:
Bu aynı zamanda çevrel çemberin merkezi (dış merkez) ile iç teğet çemberin merkezi (iç merkez) arasındaki mesafedir.[2]
Ortosentrın yanı sıra, Fuhrmann çemberi üçgenin her bir yüksekliğini bir noktada daha keser. Bu noktaların hepsi üçgenin ilgili köşelerinden uzaklığa sahiptir. Burada üçgenin iç teğet çemberinin yarıçapını gösterir.[3]
Kaynakça
[değiştir | kaynağı değiştir]- ^ Roger A. Johnson: Advanced Euclidean Geometry. Dover 2007, 978-0-486-46237-0, pp. 228–229, 300 (originally published 1929 with Houghton Mifflin Company (Boston) as Modern Geometry).
- ^ Eric W. Weisstein, Fuhrmann Circle (MathWorld)
- ^ Ross Honsberger: Episodes in Nineteenth and Twentieth Century Euclidean Geometry. MAA, 1995, pp. 49-52
Konuyla ilgili okumalar
[değiştir | kaynağı değiştir]- Nguyen Thanh Dung (2016), "The Feuerbach Point and the Fuhrmann Triangle" (PDF), Forum Geometricorum, 16, ss. 299-311
- J. A. Scott (Temmuz 2002), "An Eight-Point Circle", The Mathematical Gazette, 86 (506), ss. 326-328, JSTOR 3621878
- Roger A. Johnson (2007), Advanced Euclidean Geometry, Dover, ss. 228-229, 300, ISBN 978-0-486-46237-0,
(Erstveröffentlichung 1929 bei der Houghton Mifflin Company (Boston) unter dem Titel Modern Geometry)
- Ross Honsberger (1995), Episodes in Nineteenth and Twentieth Century Euclidean Geometry, MAA, ss. 49-52
Dış bağlantılar
[değiştir | kaynağı değiştir]- "Fuhrmann circle". 16 Temmuz 2004 tarihinde kaynağından arşivlendi.
Wikimedia Commons'ta Fuhrmann çemberi ile ilgili ortam dosyaları bulunmaktadır.






