Conway'in Hayat Oyunu

Vikipedi, özgür ansiklopedi
Gosper'ın planör silahı yaratımı "planörler".

Yaşam Oyunu ya da Hayat Oyunu, 1970'te İngiliz matematikçi John Horton Conway tarafından geliştirilmiş bir hücresel otomattır. Sıfır oyunculu bir oyundur. Diğer bir deyişle bu oyun; hiçbir oyuncunun oynamadığı, insansız bir oyundur. Başlangıçtaki veriler dışında oyuna etki edilmemesi amaçlanır.

Kurallar[değiştir | kaynağı değiştir]

Yaşam Oyunu'nun evreni, sonsuz iki boyutlu dikey ızgaraların kare hücrelerinden oluşur. Hücreler, iki durumda olabilir: ölü veya diri. Her hücre, yatay, dikey veya çapraz olarak bitişik olan sekiz komşusuyla doğrudan etkileşim kurar. Herhangi bir hücre için her adımda aşağıdaki değişikliklerden biri gerçekleşir:

  • Bir canlı hücrenin, ikiden daha az canlı komşusu varsa "yalnızlık nedeniyle" ölür.
  • Bir canlı hücrenin, üçten daha çok canlı komşusu varsa "kalabalıklaşma nedeniyle" ölür.
  • Bir canlı hücrenin, iki ya da üç canlı komşusu varsa değişmeden bir sonraki kuşağa kalır.
  • Bir ölü hücrenin tam olarak üç canlı komşusu varsa yeni bir canlı hücre oluşturur.

Başlangıçtaki dağılıma sistemin tohumu denir. Birinci kuşak, üstteki kuralların eş zamanlı olarak "tohum"daki her hücreye uygulanmasıyla elde edilir.-canlanmalar ve ölümler tek bir anda oluşur. Bu bir sonraki kuşağa geçiş adımına bazen "tık" adı verilir. (başka bir deyişle, her kuşak yalnızca bir önceki kuşaktaki dağılımın bir sonucudur). Bu kurallar daha fazla kuşak yaratmak için aynı şekilde art arda uygulanır.

Kökeni[değiştir | kaynağı değiştir]

Conway, kendisinin kopyasını yapabilen varsayımsal bir makine bulmak için denemeler yapan ve kartezyen ızgarası üstünde çok karmaşık kurallarla işleyen bir mekanizma gibi matematik modeli bulduğu zaman başarılı olan ünlü matematikçi John Von Neumann'ın 1940'larda sunduğu bir problem ile ilgilendi. Conway Von Neumann'ın düşüncesini basitleştirmeyi denedi ve neticede başardı. Önceki başarısı ile Leech'in problemini kendini türeten mekanizma hakkında von Neumann'ın düşüncelerindeki ilgisi ile birlikte bir grup teoride birleştirerek Conway "the Game of Life"ı tasarladı.

Bunun Amerikan Bilimleri'nin Ekim 1970 sayısında Martin Gardner'in "Matematik Oyunları" köşesinde ilk halk gösterimi yapıldı. Görüşün bir teorik noktasından dolayı bu ilginçti çünkü bu Turing makinesinin gücüne sahipti: Conway'in Hayat Oyun'una algoritmik olarak herhangi bir şey hesaplatılabiliyordu. Gardner yazısında:

“ Bu oyun Conway hemen meşhur yapacak, ama hem de bütün matematik araştırmalarının yeni alanlarıyla görüşmeye başladı, hücresel özdevinirin alanı (...) yaşama benzer şekilde yükselme, düşüş ve yaşayan organizmanın toplumunun değişimi sebebiyle, bu 'simülasyon oyunları' denilen gelişen kategorinin içine ait (gerçek yaşam süreçlerine benzeyen oyunlar) „

Yayınlanmasından beri, gelişebilen kalıpların şaşırtıcı yoluyla çok ilgi çekiyor. Yaşam ortaya çıkmanın ve kendinden organizasyonun bir örneğidir. Bu çok kolay kuralların yaşama geçiminden karmaşık kalıplar ortaya çıkabildiği yolu gözlemek için fizikçi, ekonomist, matematikçi, filozof, biyolog, üretken bilimlerin ve diğerleri için Conway'in Hayat Oyunu ilgi çekicidir.

Conway'in hayat oyununa marketlerde satışa sunulan ucuz yeni minibilgisayarların yeni nesilleri için zamanda oluşa gelmesi gerçeği, gecede başka türlü kullanılmamış bu makinelerin üstünde saatlerce çalışabilmesi anlamında, yardım etti. Bu itibar daha sonraki bilgisayar fraktal yapılarının tutulmasının habercisi oldu. Birçok meraklı için yaşam sadece bir programlama uğraşısı, CPU döngülerini israf etmek için eğlenceli bir yoldu. Ama bazıları için, yaşam çok filozofik yan anlamlara sahipti. Bu 1970'ler ve sonrasında bir moda takip geliştirdi; güncel gelişmeler yaşam panosunun sınırlarının içindeki bilgisayar sistemlerinin teorik taklitlerinin yaratımına kadar vardı.

Önemli deneylerden sonra Conway 3 kritere göre dikkatlice kurallarını seçmiştir:

  1. Sınırsız nüfusu büyümeyen bir basit geçirmez (kanıt) için başlangıç kalıpları olmamalıdır.
  2. Görünüşe göre sınırsız büyümeyen başlangıç kalıpları olmalıdır.
  3. Aşağıdaki mümkün yollarda sona varmadan önce bir önemli zaman periyodu için değişen ve büyüyen basit başlangıç kalıpları olmalıdır:
    • Yavaş yavaş tamamen yok olma (aşırı kalıplaşmadan veya seyrekleşen oluşundan); veya
    • İki veya daha çok periyotun sonsuz döngüsünde tekrar eden sallanan kalıpları katarak veya ondan sonra değişmeden kalan sabit bir biçime yerleşme.

Kalıpların örnekleri[değiştir | kaynağı değiştir]

Bir "planör"'ün evrimi ve hareketi

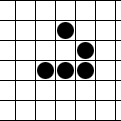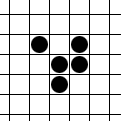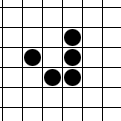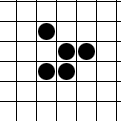
Yaşam Oyunu'nda: durağan kalıplar (natürmort), tekrar eden kalıplar ("osilatör") aynı yönde kendilerini çeviren kalıplar (uzay gemisi) gibi birçok farklı türde kalıp vardır.

                              
Blok Kayık Fırıldak Kara kurbağa Planör LWSS Pulsar

Blok ve kayık hareketsiz yaşam, "fırıldak" ve kara kurbağa" çift fazlı osilatör, ve planör ve LWSS zamanın geçmesi gibi, muntazam ızgaraların içinden yollarında yürüyen uzay gemisidirler. Pulsar çok yaygın 3 periyodlu osilatördür. İki perüyodlu doğal meydana gelen iki peiyodlu osilatörlerin büyük çoğunluğu, fırıldak ve kara kurbağa gibidir, ama 4, 8, 15, 30, ve birkaç diğeri nadir fırsatlarda görür.

Çok yaşlı adam denilen kalıplar uzun periyotlar için önce tekrar ederek gelişebilir. "Tutucu" bir kalıp 130 nesilden veya basamaktan önce genelde kaybolur. “Meşe palamudu” en azından 25 “planör” ve birçok “asilatör” gibi istiklar sağlayıcı üretmek için 5206 nesil alır.

     
Tutucu Meşe palamudu

Conway başlangıçta kalıpsızlıktan süresiz büyüyebilmeye –i.e., bir sınırlı sayıda yaşayan hücre ile herhangi bir önceki kurulumun, nüfusun sınırlı limitin ötesine büyüyememesine dayanır. Matematiksel oyunlarının içinde oyunun özgün ortaya çıkışında, Conway 1970'in sonundan önce varsayımı kanıtlayana veya çürütene 50$ ödül teklif eder. Çürütmenin bir yolu da karşıtlıkları ekleyerek alanda tutan kalıpları keşfetmek olacaktır: hareket eden “planör” veya lokomotif gibi bir nesneye defalarca ateş etmeye yapılandırılmış, hareket eden ama arkasında kalıcı "duma"nın izini bırakmaya yapılandırılmış olan bir "silah".

Ödülü aynı yılın Kasımında Massachusetts Institute of Technology'den Bill Gosper'ın liderliğinde bir grup kazandı; Gosper silahı, 15'inci nesil ilk planörü olan üretimi, ve her 30’ncu nesilden sonra başka planör aşağıda gösterilmiştir:


Gosper Planör Silahı

Sonsuz büyümenin sergisinin basit kalıpları daha sonra bulundu. Tüm üç aşağıdaki kalıpların her üçü süresiz büyür: ilk iki her motoru açan bir "blok-döşeme" yaratırken üçüncüsü iki yaratır. İlki sadece 10 yaşayan hücreye (minimum olduğu kanıtlanan) sahiptir. İkinci 5x5 bir kare formundadır. Üçüncüsü sadece bir hücre yüksekliğindedir:

    

Sonraki buluşlar sabit ve planörler veya diğer uzaygemileriyle çarpışan, "silahlar"ı ; "bir döküntü izinin arkasında yaşam boyunca hareket eden, “balonbalıklar"ı; ve hareket eden ve uzay gemilerini yollayan, "tırmıklar"ı içerir. Hem de Gosper "üretici" denen, silahların izlerinin arkasından yaşayarak çalışan, asimptotik olarak en uygun ikinci dereceden büyüme oranı tertip eder.

İlginç yollarda diğer nesnelerden planörlerin etkilenmesi mümkündür. Örneğin eğer sadece doğru yolda iki planör bir engelde çarpışırlarsa, engel planörün kaynağına daha yakın hareket edecektir. Bu "kayan hafıza engeli" bir karşıtlığı taklit etmek için kullanılır. Bunun planörleri kullanarak VE, VEYA, ve DEĞİL gibi mantık kapıları inşa etmesi mümkündür. İki karşıtlığa bağlı bir sonlu hal makinesi gibi davranan bir kalıp yapması mümkündür. Bu Turing makinesi gibi aynı sayısal güce sahiptir. Böylece Hayat Oyunu herhangi sınırsız hafızalı bilgisayar kadar güçlüdür: bu eksiksiz Turing’dir.

Dahası, orijinal kalıpların kopyalarını içererek, bir kalıp inşa edilen yeni nesnelerle birleşen bir silahlar koleksiyonunu içerebilir. Kendinin birçok kopyasını kapsayan Turing eksiksiz bilgisayarını içeren ve karışık nesnelerin birçok türünü inşa edebilen bir "evrensel inşaatçı" inşa edilebilir. Bu yapıların tanımlamaları kazanan yollarda Conway, Elwyn Berlekamp ve Richard Guy tarafından verirdi.

Yineleme[değiştir | kaynağı değiştir]

Izgaranın üstündeki bir rastgele yaşayan başlangıç kalıplarından dolayı gözlemciler nesiller yanında imlerken sürekli değişerek nüfusu bulacaklardır. Kalıplar üzerine düşünülmüş güzelliğin bir formu olabilen basit kurallardan ortaya çıkar. Simetrik olmayan başlangıçlar simetrik olma eğilimi ile izole edilmiş küçük alt kalıplardır. Bollukta bu bir kez artabilir simetri olur, ama bir yakın kalıp düzenini bozmak için yakına gelmedikçe, kaybettirilemez. Birçok sebepte tüm yaşayan hücrelerin yok olmasıyla toplum sonuncunda ortadan kaybolur, buna rağmen birçok büyük nesil için bu olmayabilir. İki veya birçok durum arasında sonsuza kadar salınan sabit biçimler veya kalıplardan birini üreterek çoğu başlangıç kalıbı sonunda "yanar"; hem de birçoğu başlangıç konumundan belirsizce uzaklara giden bir veya daha çok “planör” veya “uzay gemisi” üretir.

Algoritmalar[değiştir | kaynağı değiştir]

Yaşam Oyununun en erken sonuçları bilgisayarların kullanımı dışında elde edildi. Grafik kâğıtları, kara tahtalar, cismi oyun tahtalarında (go gibi) ve onun gibileri kullanılarak çeşitli kaderlerin küçük başlangıç kurulumları izlenir iken basit “osilatörler” ve “durgun-yaşamlar” keşfedildi. İlk araştırmalar boyunca, Conway F-pentomino (onun “R-pentomino” dediği) nesillerin küçük bir sayısı içinde dengede başarısız olduğu keşfetti.

Bu keşifler dünya üstündeki bilgisayar programlarına Yaşam kalıplarının evriminin izinde programlar yazmak için ilham verdi. Biri güncel nesilleri tutmak için ve biri içinde olan ardıllarını hesaplamak için tipik tarzda iki sıra kullanıldı. Çoğunlukla 0 ve 1 sırasıyla ölü ve yaşayan hücreleri temsil etti. Bir çift döngü, her ardıl dizlerin uygun elemanlarının 0 veya 1 olup olmadığına karar vermek için her hücrenin yaşan komşu hücresini sayarak döngü içinde güncel dizilerin her elamanını hesaba katar. Ardıl diziler gösterildi. Gelecek tekrarlama için diziler, gelecek tekrar için güncel dizi olan son tekrar içindeki ardıl diziler için görevleri değiş tokuş ettirir.

Basit şema için Minör artırımların çeşitleri olanaklıdır ve gereksiz hesapları kaydetmek için birçok yol vardır. Bir hücre son zaman basamağında ve onun değişmiş komşularının hiçbirinde değişmeyen, en uygun güncel zaman adımında değişmeyeceğine garanti edilmiş, yani güncellenmeyen hareketsiz bölgelerden geçerek zamanı kayıt edebilen aktif alanın izlerini tutan bir programdır.

Prensipte, yaşam alanı sonsuzdur ama bilgisayar sonlu hafızaya sahiptir ve çoğunlukla ileride sıranın boyutları bildirilmelidir. Sıranın sınırında aktif bölgeler haddini aştığında bu problemlere yol gösterir. Bu problemleri adreslemek için programcılar birçok stratejiye sahiptir. En basit strateji basit olarak her hücrenin dışındaki ölü dizileri varsaymaktır. Bu program için basittir ama aktif bölge sınırı geçtiği zaman, yanlış sonuçlar gösterir. Bir karışık hile bir halka diziden kar sağlayarak beraber dikili olan alanların sağ ve sol kenarlarını, ayrıca köşelerin dibi ve zirvesini üzerinde düşünmektir. Sonuç karşı köşede bir yeniden görünen arazinin kenarına çaprazlama hareket eden aktif bölgelerdir. Eğer kalıp çok geniş büyürse, Ama en azından patolojik kenar etkisi yoktur, yine de yanlışlık meydana gelebilir. Dinamik belleğin paylaşımının teknikleri ayrıca büyüyen kalıpları tutmak için durmadan genişleyen diziler yaratarak kullanılabilir.

Alternatif olarak, programcı yaşayan hücreleri gösteren koordinat çiftlerinin bir vektörü gibi bir farklı veri yapısı kullanabilir ve iki boyutlu bir dizi ile Yaşam alanlarını gösteren kavramlardan vazgeçebilir. Bu yaklaşım nüfusun yaşayan koordineli dizinin büyüklüğünü geçmedikçe kalıplara engellenmemiş alanların çevresinde hareket etmelerine izin verir. Dezavantajı simülasyonun hızı yavaşlayarak yaşayan hücreleri saymak bir arama işlemi haline gelir. Karmaşık veri yapıları ile bu problem büyük ölçüde çözülebilir.

Geniş kalıpları keşfetmek için fevkalade zaman derinlikleri, Hashlife gibi karışık algoritmalar yararlı olabilir.

Yaşamda varyasyonlar[değiştir | kaynağı değiştir]

Yaşamın orijinal başlangıcından beri, yeni kurallar geliştirirdi. Standart Yaşam Oyunu içinde, eğer bir hücre kesin olarak 3 komşuya sahipse, bir hücre "doğmuş" olur, eğer 2 veya 3 yaşayan komşuya sahipse ve başkalarını öldürüyorsa, hayatta kalır, "23/3" gibi sembolize edilir. Bir hücrenin devam etmesi için sayıların listesi veya ilk sayı gerekir. İkinci set için doğum gereklidir. Bu nedenle "16/6" "eğer 6 tane komşu var ise bir hücre doğar ve eğer 1 veya 6 komşudan herhangi biri varsa geçinir" anlamına gelir. Yüksek Yaşam bu nedenle 23/36 olur, çünkü içinde 6 tane komşusu vardır, üstelik orijinal oyunun 23/36 kuralı bir doğuşu yaratır. Yinelemelerinden dolayı Yüksek Yaşam en iyi olarak bilinir. İlaveten bu evrenlerin geniş çoğunluğunun kaotik veya metruk olmasına rağmen varyasyonlar yaşamda var olur.

Bir 2D altı köşeli Yaşam Oyunundan 48-adım oskilatör'ün örneği (kural 34/2).

Dikkate değer yaşam programları[değiştir | kaynağı değiştir]

Yüzlerce çevrimiçi yaşam programı var iken, bir liste burada karşılanamaz. Nadir veya popüler özellikler gibi önemli bazı isteklere göre cüzi sayıda programın bir seçkisi aşağıdadır. Bu çoğu program Yaşam ve diğer CA kurallarında ilginç kalıpların bir geniş kütüphanesi ve Yaşamı içeren çoklu kuralları simüle edebilmek için yeteneği, kalıpları düzenlemek ve simülasyon için grafik kullanıcı arabirimi içerir.

Dış bağlantılar[değiştir | kaynağı değiştir]

Birçok dış bağlantı the Open Directory Project'de Conway'in Hayat Oyunu10 Eylül 2005 tarihinde Wayback Machine sitesinde arşivlendi. dayanabilen Hayat Oyununu içerir. Ayrıca, Hayat Oyununun Haberleri 1 Temmuz 2007 tarihinde Wayback Machine sitesinde arşivlendi. birçok bireysel tarafından son gelişmeleri rapor ederek bir web günlüğü olur.

Bazı ek bağlantılar:

"https://tr.wikipedia.org/w/index.php?title=Conway%27in_Hayat_Oyunu&oldid=30939755" sayfasından alınmıştır