Trilineer interpolasyon

Trilineer interpolasyon, 3-boyutlu bir grid üzerinde çok-değişkenli bir interpolasyon metodudur. Trilineer interpolasyon, sıklıkla, nümerik analiz, veri analizi ve bilgisayar grafiklerinde kullanılır.

Lineer ve bilineer interpolasyonlar ile kıyası[değiştir | kaynağı değiştir]

Trilineer interpolasyon, $D=1$ boyuttaki lineer interpolasyon ve $D=2$ boyuttaki bilineer interpolasyonun, $D=3$ boyutundaki uzantısıdır. Bu interpolasyon metotlarının doğruluk seviyesi (order of accuracy) 1'dir. Yanı sıra, bu metot, interpole edilecek noktanın çevresinden $(1+n)^{D}=8$ nokta değerine ihtiyaç duyar.

Birçok yöntemle, trilineer interpolasyon denklemini türetmek mümkündür. Trilineer interpolasyon, 3-boyutlu 1.seviye B-spline interpolasyon tensörüne denktir. Ayrıca, interpolasyon operatörü, 3 lineer interpolasyon operatörünün tensörel çarpımına eşittir.

Metot[değiştir | kaynağı değiştir]

Periyodik ve kübik bir latis üzerinde, $x_{d}$ , $y_{d}$ ve $z_{d}$ 'nin, $x$ , $y$ , $z$ 'in her biri ile daha küçük bir koordinatın arasındaki fark olduğunu düşünelim:

\ x_{d}=(x-x_{0})/(x_{1}-x_{0})

\ y_{d}=(y-y_{0})/(y_{1}-y_{0})

\ z_{d}=(z-z_{0})/(z_{1}-z_{0})

$x_{0}$ , latis üzerinde $x$ 'den küçük bir nokta ve $x_{1}$ , $x$ 'den büyük bir noktadır. Aynı durum, $y_{0},y_{1},z_{0}$ ve $z_{1}$ için geçerlidir.

İlk olarak, $x$ -doğrultusunda interpolasyon yapılır (kübün ön yüzünün arka yüze doğru itildiğini düşünün). Sonucunda:

\ c_{00}=V[x_{0},y_{0},z_{0}](1-x_{d})+V[x_{1},y_{0},z_{0}]x_{d}

\ c_{01}=V[x_{0},y_{0},z_{1}](1-x_{d})+V[x_{1},y_{0},z_{1}]x_{d}

\ c_{10}=V[x_{0},y_{1},z_{0}](1-x_{d})+V[x_{1},y_{1},z_{0}]x_{d}

\ c_{11}=V[x_{0},y_{1},z_{1}](1-x_{d})+V[x_{1},y_{1},z_{1}]x_{d}

$V[x_{0},y_{0},z_{0}]$ , $(x_{0},y_{0},z_{0}).$ noktasındaki fonksiyon değeridir. İkinci olarak, $y$ -doğrultusunda interpolasyon yapılır (kübün üst kenarının alt kenarına doğru itildiğini düşünün). Sonuçta:

\ c_{0}=c_{00}(1-y_{d})+c_{10}y_{d}

\ c_{1}=c_{01}(1-y_{d})+c_{11}y_{d}

Son olarak, denklem $z$ -doğrultusunda interpole edilir (geride kalan çizgi boyunca ilerlendiğini düşünün):

\ c=c_{0}(1-z_{d})+c_{1}z_{d}.

Bu ifade, interpole edilen noktadaki fonksiyon değerini vermektedir.

Trilineer interpolasyonun sonucu, üç farklı eksende yapılan üç lineer interpolasyonun işlem sırasından bağımsızdır. Örneğin, işlem sırası $x$ , $y$ , $z$ olan bir trilineer interpolasyonunun sonucu, işlem sırası $y$ , $z$ , $x$ olan interpolasyon ile aynıdır.

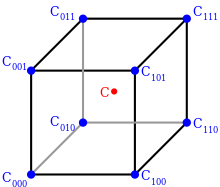
Yukarıdaki işlemler şu şekilde de görselleştirilebilir: İlk önce, interpole edilecek noktayı kapsayan bir kübün sekiz köşe noktasının koordinatları bulunur. Bu köşe noktaları, varsayılsın ki, şu değerlere sahiptir: C000, C100, C010, C110, C001, C101, C011, C111.

Akabinde, C00'ı bulmak için C000 ve C100 ile lineer interpolasyon yapılır. Lineer interpolasyon, aynı şekilde, C01 için C001 ve C101 arasında; C11 için C011 ve C111 arasında; ve C10 için C010 ve C110 arasında uygulanır.

Ardından, C0 için C00 ve C10 arası; ve C1 için C01 ve C11 arası lineer interpolasyon uygulanır.

Son adımda, C değeri, C0 ve C1 arasında lineer interpolasyonla elde edilir.

Tüm bunlara ek olarak, trilineer interpolasyon, iki bilineer interpolasyon ve bir lineer interpolasyonun kombinasyonu ile de ulaşılabilir:

C\approx \ l(b(C_{000},C_{010},C_{100},C_{110}),b(C_{001},C_{011},C_{101},C_{111}))

Ayrıca bakınız[değiştir | kaynağı değiştir]

Dış bağlantılar[değiştir | kaynağı değiştir]

İnvers iteratif trilineer interpolasyon için NASA'nın yayımladığı bir kodsu10 Ekim 2006 tarihinde Wayback Machine sitesinde arşivlendi..
Paul Bourke, Interpolation methods26 Ağustos 2012 tarihinde Wayback Machine sitesinde arşivlendi., 1999. Yayın, trilineer interpolasyon için ikili mantık sistemine dayanan basit ve etkili bir yöntem sunmaktadır. Ayrıca, metot, n-boyuta genişletilebilir (ör. tetralineer, pentalineer vb.).