Eşevreli haller

Fizikte, Kuantum mekaniğinde, eşevreli hal klasik harmonik salıngaca benzeyen kuantum harmonik salıngacının nicel hareketidir. Kuantum dinamiğinin Erwin Schrödinger tarafından Scrödinger denklemlerine çözüm ararken 1926 yılında türetilen ilk örneğidir. Örneğin, eşevre hali parçacığın salınımsal hareketini açıkları. Bu haller, John R. Klauderin ilk makalelerinde alçalma operatörü ve fazla tamamlanmış aile teşkili olarak özvektör adında tanımlanmıştır. Eşevre halleri,[ışığın kuantum kuramında (kuantum elektrodinamiği) ve diğer bozonik kuantum alanlarında Roy J. Glauber’in 1963 yılındaki çalışmaları tarafından geliştirilmiştir.Salınan alanın eşevre hali, klasik sinüs dalga hareketine benzeyen, devamlı lazer dalgası gibi olan kuantum halidir. Ancak, eşevre hali kavramı kayda değer biçimde genellenmiş ve sinyal sürecini niceleme, görüntü işleme alanlarında matematiksel fizikte ve uygulamalı matematik oldukça geniş ve önemli bir konu olmuştır. Bu hususta, kuantum harmonik salıngacı ile bağlantılı eşevreli haller genel olarak standart eşevreli haller ya da Gauss işlevi halleri olarak anılır.

Kuantum Optiğinde Eşevreli Haller

Figure 1: Optiksel homodin deteksiyonu tarafından ölçülen Elektrik Alan, üç eşevreli halin fazlarının fonksiyonu olarak optiksel homodin deteksiyonu ile ölçülen elektriksel Nd:YAG lazeri tarafından yansıtılmış

Figure 2: İkinci eşevreli hale göre salınan dalga demeti.

Figure 3: Eşevreli hale göre Wigner fonksiyonu.

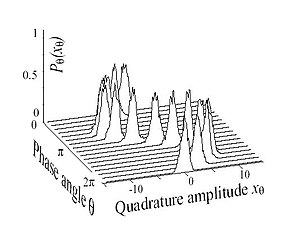
Kuantum mekaniğinde, eşevreli hal kuantum halinin kuantum harmonik salıngacına, elektromanyetik alana vs. uyarlanabilen özelleşmiş halidir, bu durum maksimal sayıda bağlaşımı ve klasik türde davranışı tanımlar. Erwin Schrödinger, Gauss işlevini en küçük sayıda belirsizlikle 1926 yılında türetirken Schrödinger denklemlerine çözüm bulma yolunda benzerlik prensibine uyumlu olmasını sağlamaya çalışırken eşevreli halleri bulmuştur. Bu en küçük belirsizlik durumu, göreceli saçılım yapmak için konum ve momentuma eşit olacak ve hepsi de eşit küçüklükte yüksek enerjide başlayacak şekilde tek bağımsız katsayılı seçilmiştir. Dahası, sistemin enerji özdurumuna karşı olacak şekilde eşevreli hal için zaman evrimi klasik münhaniler şeklinde yoğuşur. Kuantum doğrusal harmonik salıngacı ve bu yüzden eşevreli dorumlar fiziksel sistemlerin kuantum kuramı olarak doğmuştur. Bunlar ışığın kuantum kuramında (kuantum elektrodinamiği) ve diğer bozonik kuantum alan kuramlarında bulunurlar.Dalga demetleri olarak bilinen en küçük Gauss işlevi belirsizliği, Roy J. Glauber ‘e kadar yani elektromanyetik alandaki eşevreli kuantum kuramsal tanım tamamlanana kadar çok fazla dikkat çekmemiştir. Bu hususta, E.C.G Sudarshan’ın uyumlu katkıları da kaldırılmamıştır. Glauber, E.C.G Sudarshan’a yaptığı bu yardımı Hanbury-Brown& Twiss deneyine tanım sağlamak amacıyla yapmıştır. Bu tutunuma açıklama getirmek için çok önemli kapıları açmıştır. Klasik optikte ışık bir kaynaktan gönderilen elektromanyetik dalga olarak kabul edilir. Genellikle, tutunum lazer ışığının farklı dalga fazları olan kaynaklar tarafından yansıtılan ışık olduğu kabul edilir. Aslında, kuantum kuramı için eşevreli fotonların resmi kuantum kuramından başka bir faz için doğru olmaz. Lazer ışınımı, rezonans bir oyukta salınım frekansına eşit olan atomik elektron geçişiyle üretilen enerjiden alana uçarak üretilir. Enerji salınım halindeyken, uyarılmış salınım ihtimali için olan ihtimali yükseltir. Bu üstel büyüme, salınım halinde olan, üstel olarak doğrusal olmayan etkiler onu sınırlayana kadar artan pozitif bir geribildirimdir. Karşıt bir örnek olarak, modların süreci olarak salınan ampül ışığı söylenebilir. Salınım süreci uzay ve zaman açısından oldukça rastgeledir. Ancak, bir lazerde, ışık salınım modunda yayılır ve bu modu oldukça eşevreli hale getirir. Bu yüzden, lazer ışığı eşevreli hal olarak kabul edilir. Doğrusal harmonik salıngacın enerji özdurumu (ipteki kütleler, katıdaki kafes titremesi, elektromanyetik alandaki salınımlar, moleküllerdeki çekirdeklerin titremesi) düzeltilmiş kuantum halleridir. Fock hali (tek foton) en parçacıksal haldir; sayıları düzeltilmiş parçacıklar ve belirsiz fazlara sahiptir. Eşevresel halde kuantum mekaniksel belirsizlik, momentum, konum ve fazlarda eşittir ve genlikleri hemen hemen aynıdır. Matematiksel olarak, eşevre hali, $|\alpha \rangle$ , imha operatörünün, ${\hat {a}}$ , sağ özdurumu olarak tanımlanır ve özdeğeri $\alpha$’dır. Denklemsel olarak şöyle okunur;

${\hat {a}}|\alpha \rangle =\alpha |\alpha \rangle$

${\hat {a}}$ hermityan olmadığından $\alpha$ karmaşık sayıdır. Şu şekilde gösterilebilir;

$\alpha =|\alpha |e^{i\theta }~~~,$

$~|\alpha |~$ ve $~\theta ~$ halin fazı ve genliği olarak adlandırılır. Birçok eşevreli hal olduğunda $~|\alpha \rangle ~$ durumu standart eşevre hali olarak adlandırılır. Fiziksel olarak, bu denklem eşevre halinin ortaya çıkarma ya da imha etme tarafından değiştirilemediği anlamına gelir. İmha operatörünün özdurumu Poissonian sayı dağıtımıdır. Poisson dağıtımı tüm ortaya çıkmaları birbirinden bağımsız hale getiren gerekli ve önemli bir durumdur. Tek parçacık durumu ($|1\rangle$ Fock durumu) bir parçacığın saptanmasoyla başkasının saptanma ihtimalinin sıfır olmasıyla oluşur.Bu boyutsuz operatörlerin türetilmesi, kuantum optiğinde, $~X~$ ve $~P~$ genelde alan tümlevi olarak adlandırılır. Operatörler kütle $~m~$ ve sabit $~k~$ ‘nın momentum ve konumuna bağlıdır:

${P}={\sqrt {\frac {1}{2\hbar m\omega }}}\ {p}{\text{,}}\quad {X}={\sqrt {\frac {m\omega }{2\hbar }}}\ {x}{\text{,}}\quad \quad {\text{where }}\omega \equiv {\sqrt {k/m}}.$

For an optical field, Optiksel bir alan için,

$~E_{\rm {R}}=\left({\frac {\hbar \omega }{2\epsilon _{0}V}}\right)^{1/2}\!\!\!\cos(\theta )X~$

   ve    $~E_{\rm {I}}=\left({\frac {\hbar \omega }{2\epsilon _{0}V}}\right)^{1/2}\!\!\!\sin(\theta )X~$ Elektrik alanın gerçek ve sanal modlarıdır. Bu boyutsuz operatörlerin iki system için Hamiltonianları;

${H}=\hbar \omega \left({P}^{2}+{X}^{2}\right){\text{,}}\qquad {\text{ile}}\qquad \left[{X},{P}\right]\equiv {XP}-{PX}={\frac {i}{2}}\,{I}.$ olur.

Erwin Schrödinger, en küçük belirsiz Gauss işlev dalga demetlerini ilk defa gösterdiğinde klasik durumlar arıyordu.Harmonik salıngacın nicel durumu belirsizlik ilişiğini belirsiz eşit dağılımla en küçüğe indirgeyen $~X~$ ve $~P~$ operatörlerine sahiptir.

$\left({X}-\langle {X}\rangle \right)\,|\alpha \rangle =-i\left({P}-\langle {P}\rangle \right)\,|\alpha \rangle {\text{,}}\qquad {\text{ya da}}\qquad \left({X}+i{P}\right)\,\left|\alpha \right\rangle =\left\langle {X}+i{P}\right\rangle \,\left|\alpha \right\rangle$..

Bu $({X}+i{P})$ operatörünün özdurumudur. (Eğer belirsizlik $~X~$ ve $~P~$ arasında dengeli değilse buna sıkıştırılmış eşevre durumu denir). Schrödinger en küçük belirsiz durumları doğrusal harmonic salıngacın $~(X+iP)~$’nin özdurumu olması için bulmuştur ve çoklu-foton durumları için bu gösterimi kullanmış, Glauber ise tamamlanmış eşevre durumlarını elektrik alan imha operatörünün sağ özdurumu olacak şekilde sırası ile bulmuştur. Eşevre durumu Glauber’in çalışmalarından sonra kök salmıştır. Eşevre durumunun karmaşık düzlemdeki konumu genliği ve fazı, $~\theta ~$, aynı olan klasik salıngacın momentum ve konumunun ortasındadır. Figür 5’te gösterildiği üzere, belirsizlik tüm yönlere eşit dağılmış ve çapı ½ olan bir disk ile gösterilmiştir. Faz yükseldikçe eşevre durumu disk ve orijini çember içine alır ancak dağılmaz ya da saptırmaz. Bu tek bir noktanın uzaydaki fazına en çok benzeyen kuantum durumudur. Belirsizlik salınımın genliği arttıkça ½’de sabit kaldığından durum sinüs dalgasına gitgide benzemeye başlar. Boşluk durumu, $|0\rangle$, $\alpha =0$’nın eşevre durumu olduğu için tüm eşevreler boşlukta aynı düzeyde belirsizdir. Bu yüzdem boşluktaki dalgalanmalardan dolayı eşevre durumu kuantum gürültüsü olarak ifade edilebilir. Bu gösterim $~|\alpha \rangle ~$, Fock durumu anlamına gelmez. Örneğin, bu gösterim; $\alpha =1$ tek bir foton Fock durumu, $~|1\rangle ~$ anlamına gelmez.. Düzeltilmiş sayı durumlarının kaba foton sayısıyla birleşimini ifade eder. The formal solution of the eigenvalue equation is the vacuum state displaced to a location in phase space, i.e., it is obtained by letting the unitary displacement operator operate on the vacuum: Özdeğer eşitliklerinin boşluk durumundaki yer değiştirme konumu $\alpha$ yer değiştirme operatörünün $D(\alpha )$ birleşmesiyle ortaya çıkar:

$|\alpha \rangle =e^{\alpha {\hat {a}}^{\dagger }-\alpha ^{*}{\hat {a}}}|0\rangle =D(\alpha )|0\rangle$,

$~{\hat {a}}=X+iP~$ ve $~{\hat {a}}^{\dagger }=X-iP~$. Kolayca görülebilir ki bu Fock durumunun temelinin eşevre durumundaki yeniden gösterimidir:

$|\alpha \rangle =e^{-{|\alpha |^{2} \over 2}}\sum _{n=0}^{\infty }{\alpha ^{n} \over {\sqrt {n!}}}|n\rangle =e^{-{|\alpha |^{2} \over 2}}e^{\alpha {\hat {a}}^{\dagger }}|0\rangle$.,

where are energy (number) eigenvectors of the Hamiltonian . For the corresponding Poissonian distribution, the probability of detecting photons is:

$|n\rangle$ Hamiltonian özvektörlerinin enerji sayısıdır $H={\hat {a}}^{\dagger }{\hat {a}}+{\frac {1}{2}}$., Poissonian dağılımı için, $~n~$ sayıdaki foton için saptama ihtimali

$P(n)=|\langle n|\alpha \rangle |^{2}=e^{-\langle n\rangle }{\frac {\langle n\rangle ^{n}}{n!}}$

Aynı şekilde, eşevre durumunda ortalama foton sayısı; $~\langle n\rangle =\langle {\hat {a}}^{\dagger }{\hat {a}}\rangle =|\alpha |^{2}~$ Ve değişkeni; $~(\Delta n)^{2}={\rm {Var}}\left({\hat {a}}^{\dagger }{\hat {a}}\right)=|\alpha |^{2}~$.

Figure 4: Fotonları saptama ihtimali, foton dağılım sayısı Figür 3. Poissonian dağılım değerleri.

Büyük α’nın sınırlamalarında ortaya çıkan istatistiklerde klasik istikrarlı dalgaların tüm büyük değerleri $~\alpha ~$’ya eştir.Sonuçlar tek algılayıcıya ve ona bağlı olan sıralamadaki eşevre durumuna uygulanabilir.Ancak, birçok algılayıcı ölçülen oranlar daha yüksek sıralamadaki eşevreyi dahil etmiştir. Kuantum eşevresinin Glauber tanımındatüm n’ler için n. sırada oran fonksiyonlar vardır. Kusursuz eşevre durumu oranının n-sırası 1 e eşittir. Figür 5’teki $~\alpha \gg 1~$ , bize şunu verir; $\Delta \theta |\alpha |={\frac {1}{2}}$. Bundan görebiliriz ki; faz belirsizliği ve sayısı belirsizliği arasında değiş tokuş vardır. $\Delta \theta ~\Delta n=1/2$, bazen sayı-faz belirsizlik ilişkisi anlamına gelir. Bu resmi bir belirsizlik ilişkisi değildir; kuantum mekaniğinde eşsiz bir faz operatörü tanımlanmamıştır.

Eşevre durumunun dalga denklemi

Eşevre durumunun dalga denklemini bulmak için en kolay yol Heisenberg’in kuantum harmonik salıngacını eşrevreli duruma |α〉uyarlayarak olur.

$~a(t)|\alpha \rangle =e^{-i\omega t}a(0)|\alpha \rangle =e^{-i\omega t}\alpha (0)|\alpha \rangle ~.$

Yani Heisenberg’e göre eşevre durumu imha operatörünün özdurumudur. It is easy to see that in the Schrödinger picture the same eigenvalue occurs, Schrödinger’in eşitliğinde $~\alpha (t)=e^{-i\omega t}\alpha (0)~$ olur ve özdeğeri benzer şekilde görebiliriz ;

$~a|\alpha (t)\rangle =\alpha (t)|\alpha (t)\rangle$ .

Koordinat temsilini 〈x| yöneterek şu türetilmiş denklem elde edilebilir;

$~{\sqrt {\frac {m\omega }{2\hbar }}}\left(x+{\frac {\hbar }{m\omega }}{\frac {\partial }{\partial x}}\right)\psi ^{\alpha }(x,t)=\alpha (t)\psi ^{\alpha }(x,t)~,$

Şu şekilde kolayca sonuç verir;

$~\psi ^{(\alpha )}(x,t)=\left({\frac {m\omega }{\pi \hbar }}\right)^{1/4}e^{-{\frac {m\omega }{2\hbar }}\left(x-{\sqrt {\frac {2\hbar }{m\omega }}}\Re [\alpha (t)]\right)^{2}+i{\sqrt {\frac {2m\omega }{\hbar }}}\Im [\alpha (t)]x+i\delta (t)}~,$

δ(t) kararlaştırılmamış fazdır, bunu düzeltmek için dalga denkleminin Schrödinger’in denklemini sağlaması gerekmektedir.

Bu şunu takip eder;

$~\delta (t)=-{\frac {\omega t}{2}}+{\frac {|\alpha (0)|^{2}\sin(2\omega t-2\sigma )}{2}}~,$

σ ilk özdeğerdir yani; $~\alpha (0)=|\alpha (0)|\exp(i\sigma )$. ψ^(α) , konum ve momentumun kabaca minimal Schrödinger dalga demeti ile bulunmasıdır ve bu sayede salınım klasik sistemdeki gibi olur

$\langle {\hat {x}}(t)\rangle ={\sqrt {\frac {2\hbar }{m\omega }}}\Re [\alpha (t)]\qquad \qquad \langle {\hat {p}}(t)\rangle ={\sqrt {2m\hbar \omega }}\Im [\alpha (t)]~.$

Standart eşevre durumunun matematiksel karakteristiği

Standart eşevre durumları şu ana kadar üç ortak özellik üzerinde tanımlandı ;

1. İmha operatörlerinin özvektörü: ${\hat {a}}|\alpha \rangle =\alpha |\alpha \rangle \,$.
2. Birleştirici yer değiştirme operatörü uygulaması ile boşluktan elde edilirler: $|\alpha \rangle =e^{\alpha {\hat {a}}^{\dagger }-\alpha ^{*}{\hat {a}}}|0\rangle =D(\alpha )|0\rangle \,$ .
3. En küçük belirsizliğin durumları: < math>\Delta X = \Delta P= 1/\sqrt{2}\,</math> .

Bu özelliklerin hepsi genellemeye neden olabilir ve genelde birbirlerinde farklıdırlar. Bu duruma eşevre durumlarının Fock durumundan matematiksel olarak farklı olması açısından yaklaşırız. İki farklı eşevre durumu dikgen değildir:

$\langle \beta |\alpha \rangle =e^{-{1 \over 2}(|\beta |^{2}+|\alpha |^{2}-2\beta ^{*}\alpha )}\neq \delta (\alpha -\beta )$

Thus, if the oscillator is in the quantum state it is also with nonzero probability in the other quantum state Bu yüzden, eğer nicel durumdaki salıngaç, $|\alpha \rangle$, aynı zamanda başka bir nicel durumun sıfır olmayan ihtimali ise durum; $|\beta \rangle$ . Ancak, kapatma ilişkisine uyduklarında, her durumda eşevre durumları halinde karışabilirler. Bunlar, bu yüzden, çarprazlama olarak her durumda birleşebilen fazla tamamlanmış temellerdir. Bu Glauber P sunumlarının öncüsüdür. Nicel durumların vektör uzayında $I$ operatörü ile ifade edilebilir:

${\frac {1}{\pi }}\int |\alpha \rangle \langle \alpha |d^{2}\alpha =I\qquad d^{2}\alpha \equiv d\Re (\alpha )\,d\Im (\alpha )$.

Başka bir zorluk ise ${\hat {a}}^{\dagger }$ ‘nın öncü keti ve ${\hat {a}}$ ‘nın öncü brası olmamasıdır. Bu eşitlik teknik ölçümlerde oldukça kullanışlıdır:

$a^{\dagger }|\alpha \rangle =\left({\partial \over \partial \alpha }+{\alpha ^{*} \over 2}\right)|\alpha \rangle$

Son durum Agarwal durumu ya da foton-ekleme eşevre durumu olarak bilinir. $|\alpha ,1\rangle .$ ile gösterilir. ${n}$ sırasındaki Agarwal sıralaması; $|\alpha ,n\rangle =[{{\hat {a}}^{\dagger }]}^{n}|\alpha \rangle /\|[{{\hat {a}}^{\dagger }]}^{n}|\alpha \rangle \|$

Özdeşliğin çözümü konumun özdurumunun matrislerini, $\langle x|\cdots |y\rangle$, almakla çözümlenebilir. Sağ taraf hızla $\delta (x-y)$ verir. Sol tarafa da aynısı uygulanırsa şu ortaya çıkar;

$\psi ^{\alpha }(x,t)=\langle x|\alpha (t)\rangle$

Parçacığın momentum ve konumuna göre çözümün özdeşliği tekrar gösterilebilir. Tüm koordinatlar için $x$’in yeni tanımını

$|\alpha \rangle \equiv |x,p\rangle \qquad \qquad x\equiv \langle {\hat {x}}\rangle \qquad \qquad p\equiv \langle {\hat {p}}\rangle$

Eşevre durumunun kapatıcı ilişkisi

$I=\int |x,p\rangle \,\langle x,p|~{\frac {\mathrm {d} x\,\mathrm {d} p}{2\pi \hbar }}$

Bu tüm kuantum mekanikal beklenen değerlerinden çıkarılabilir, nicel klasik faz-uzat integrali ve açıklamasının normalleştirme faktörü $(2\pi \hbar )^{-1}$ Buna ek olarak imha operatörlerinin kesin özdurumu olması demek eşevre durumunun parçacığın konum ve momentum özdurumuna yaklaşıldı demektir:

${\hat {x}}|x,p\rangle \approx x|x,p\rangle \qquad \qquad {\hat {p}}|x,p\rangle \approx p|x,p\rangle$

Yakınsamalardaki hatalar Belirsizlik Prensibi ile ölçülür

$\langle x,p|\left({\hat {x}}-x\right)^{2}|x,p\rangle =\left(\Delta x\right)^{2}\qquad \qquad \langle x,p|\left({\hat {p}}-p\right)^{2}|x,p\rangle =\left(\Delta p\right)^{2}$

Bose-Einstein yoğunluğunun eşevre durumu

• Bose-Einstein yoğunlaşması aynı nicel durumdaki bozon atomlarının toplamından oluşur. Termodinamik bir sistemde, taban durumunun gözle görülür biçimde kritik sıcaklıkta zapt edilmesiyle oluşur— Yani de Broglie dalga boyu, atomlar arası boşluktan büyük olduğunda. Sıvı Helium-4’teki süper akışkanlığın ideal gazlardaki Bose-Einstein yoğunlaşmasıyla ilişkisi olduğuna inanılır. Ancak, ⁴He’nin güçlü etkileşimleri vardır ve sıvı yapısı factörü bunda önemli rol oynar. Eşevre durumunun kullanımı süper ⁴He’nin süper akışkan bileşenini yoğun/yoğun olmayanın parçası olarak yavaş nötron dağılımının bir sonucu olan süperakışkanlık bileşeni olarak sunar.Çoğu süper akışkanın özellikleri eşevre durumunun süperiletken bileşeni olarak seyreder.
• Süper akışkanlığın ilk çalışmalarında, Penrose ve Onsager süper akışkanlık için bir ölçev öne sürmüştür. Bu ölçev makroskobik factor bileşenlerinin birinci düzeyden indirgenmiş yoğunluk matrisi olarak gösterilmiştir. Daha sonra, C.N. Yang daha genel bir makroskobik, bozon sistemleri kadar fermiyon sistemlerini de içeren nicel eşevrelilik ortaya atmıştır. Bu sistem her sıradaki indirgenmiş yoğunluklu matrisin olduğu, büyük faktörlü bileşen (özdeğer) zamanlarda olur. Süper iletkenlik büyük faktörlü bileşenlerin olduğu birinci dereceden indirgenmiş yoğun matristir. Süper iletkenlik ikinci dereceden indirgenmiş yoğun matris içerir.
• İndirgenmiş yoğun matrislerin süper akışkanlardaki makroskobik nicelikli eşevreliliği şeklen bağlılaşım fonksiyonlarında kullanılan ışınım eşevreliliği ile aynıdır. İkisi de nicel makroskobik eşevreliliğe örnektir. Elektromanyetik alanda, makroskobik olarak büyük eşevre bileşeni ve ses Glauber’in sinyal-artı-ses açıklaması ile verilir, şeklen makroskobik büyük süper akışkan bileşeni artık normal akışkan bileşeni ile aynıdır.
• Günlük yaşamdaki elektromanyetik ışımalar, televizyon ve radio dalgaları gibi, eşevre durumlarına örnektir. Klasik ve kuantum arasındaki gelenekselliği sınırlamalıdır.
• Süper akışkanlıktaki eşevrelik helium atomlarının alt kümesine dayandırılmamalıdır; bu tüm atomları içeren toplu bir olaydır.

Süperiletkenlikte eşevre elektron durumu

• Elektronlar fermiyonlardır, ancak Cooper parçalarında çift oluşturduklarında bozon olarak davranırlar ve bu sayede düşük sıcaklıklarda topluca eşevre durumuna dönüşürler. Bu çiftleşme aslında elektronlar arasında olmaz, müsait elektronlar bu durumların içine ve dışına hareket ederler. Cooper çiftleşmesi süper iletkenliğin ilk modelidir.
• Bu eşevre durumları düşük sıcaklıkta süperiletken Kuantum Hall etkisi gibi etkilerin açıklamasının bir parçasıdır.

Geneli

• Gilmore ve Perelomov’a göre, eşevre durumlarının yapısı grup kuramında problem olarak görülebilir ve bu yüzden Heisenberg grubundan başka gruplarla etkileşime girebilir, bu da standart eşevre durumunun tartışılmasına neden olur. Dahası, bu eşevre durumları kuantum gruplarınca genellenebilir. Bu konular orijinal çalışmaya referans olur ve matematiksel fiziğin eşevre durumlarında tartışılır.
• Kuantum alan ve sicim kuramında eşevre durumlarının genellemesi bağımsızlık derecesinin sonsuz olma durumudur ve boşluk halini tanımlamak için orijinal boşluktan beklenen değerle hesaplanabilir.
• Bağımsızlığın fermiyonik derecelerinde, düşük enerji durumlarında bozonik alanın operatörünün eşevre durumu tek boyutlu çoklu kuantum sistemlerinde parçacık-boşluk uyarıları yaratabilir. Buna bozonlaştırma denir.
• Göreceli olmayan kuantum mekaniğinin Gauss işlevli eşevre durumu Klein-Gordon ve Dirac parçacıklarının göreceli eşevre durumu olarak genellenebilir.
• Eşevre durumları, aynı zamanda, kuantum kütleçekimi döngüsü ya da yarı klasik standart kuantum genel göreceliliği ile ilgili çalışmalarda da görülür.