Blok şifre çalışma kipleri
Kriptografide çalışma kipleri, bir blok şifrenin tek bir anahtar altında güvenli bir şekilde tekrarlı kullanımına olanak veren yöntemlerdir.[1][2] Değişken uzunluktaki mesajları işlemek için veriler ayrı parçalara bölünmelidir. Son parça şifrenin blok uzunluğuna uyacak şekilde uygun bir tamamlama şeması ile uzatılmalıdır. Bir çalışma kipi bu bloklardan her birini şifreleme şeklini tanımlar ve genellikle bunu yapmak için ilklendirme vektörü (IV) olarak adlandırılan rastgele oluşturulmuş fazladan bir değer kullanır.[1]
Çalışma kipleri özellikle şifreleme ve kimlik doğrulamada kullanılmak üzere oluşturulmuştur.[1] [3] Tarihsel olarak çalışma kipleri çeşitli veri değiştirme senaryoları altında hata yayılma özellikleri bakımında geniş bir biçimde çalışılmıştır. Bütünlük koruması şifrelemeden tamamen farklı bir kriptografik amaç olarak doğmuştur. Kimlik doğrulamalı şifreleme kipi olarak bilinen bazı modern çalışma kipleri şifreleme ve kimlik doğrulamayı verimli bir şekilde birleştirmiştir.
Çalışma kipleri çoğunlukla simetrik şifrelemeyle ilişkilendirilmiş olsa da teoride RSA gibi açık anahtarlı şifreleme yöntemlerinde de kullanılabilir. (Ancak uygulamada uzun mesajların açık anahtarla şifrelenmesi genellikle melez şifreleme kullanılarak yapılır.).
Tarihçe ve standartlaşma[değiştir | kaynağı değiştir]
İlk çalışma kipleri ECB, CBC, OFB ve CFB 1981 yılına kadar dayanır ve FIPS 81, DES Modes of Operation'da tanımlanmıştır. 2001 yılında NIST SP800-38A22 Temmuz 2017 tarihinde Wayback Machine sitesinde arşivlendi., Recommendation for Block Cipher Modes of Operation ile CTR kipini ve AES blok şifresini ekleyerek onaylanmış çalışma kiplerini güncellemiştir. Son olarak NIST 2010 Ocak ayında SP800-38E13 Ağustos 2011 tarihinde Wayback Machine sitesinde arşivlendi., Recommendation for Block Cipher Modes of Operation: The XTS-AES Mode for Confidentiality on Storage Devices ile XTS-AES kipini eklemiştir. NIST tarafından onaylanmamış başka çalışma kipleri de mevcuttur. Örneğin CTS (ciphertext stealing) kipi birçok popüler kriptografik kütüphanede bulunur.
ECB, CBC, OFB, CFB, CTS ve XTS kipleri sadece gizlilik sağlar; şifrelenmiş bir mesajın yanlışlıkla değiştiğinden ya da kasıtlı olarak oynanmadığından emin olmak için CBC-MAC gibi bir mesaj doğrulama kodu'na ihtiyaç vardır. Kriptografi topluluğu bir bütünlük kipinin gerekliliğinin farkına vardı ve NIST de HMAC, CMAC ve GMAC ile buna karşılık verdi. HMAC 2002'de FIPS 1988 Nisan 2011 tarihinde Wayback Machine sitesinde arşivlendi., The Keyed-Hash Message Authentication Code (HMAC) olarak onaylandı, CMAC 2005'te SP800-38B 26 Mayıs 2012 tarihinde Wayback Machine sitesinde arşivlendi., Recommendation for Block Cipher Modes of Operation: The CMAC Mode for Authentication ile tanımlandı ve GMAC 2007 yılında SP800-38D5 Ağustos 2011 tarihinde Wayback Machine sitesinde arşivlendi., Recommendation for Block Cipher Modes of Operation: Galois/Counter Mode (GCM) and GMAC ile onaylandı.
Bir gizlilik kipini ve bütünlük kipini birleştirmeye çalışmanın güç ve hataya yatkın olmasının farkına varılmasıyla kriptografi topluluğu gizlilik ve bütünlüğü bir arada sağlayan kipler sunmaya başladılar. Bu kipler kimlik doğrulamalı şifreleme olarak bilinir. Örnekleri CCM (SP800-38C5 Ağustos 2011 tarihinde Wayback Machine sitesinde arşivlendi.), GCM (SP800-38D5 Ağustos 2011 tarihinde Wayback Machine sitesinde arşivlendi.), CWC, EAX, IAPM ve OCB'dir.
Çalışma kipleri günümüzde ulusal ve uluslararası standart kuruluşları tarafından tanımlanmaktadır. Bunların başında NIST[kaynak belirtilmeli] gelmektedir. Diğer önemli standart kuruluşları ISO, IEC, IEEE, ANSI ve IETF'dir.
İlklendirme vektörü (IV)[değiştir | kaynağı değiştir]
İlklendirme vektörü (IV) çeşitli kipler tarafından şifrelemeyi rassallaştırmak için kullanılan ve dolayısıyla aynı açık metnin tekrar şifrelendiği durumlarda anahtar değiştirmeden farklı şifreli metin üretilmesini sağlayan bir bit blokudur. İlklendirme vektörünün güvenlik gereksinimleri anahtardan farklıdır, IV genellikle gizli olmak zorunda değildir. Ancak birçok durumda bir IV'in aynı anahtar ile tekrar kullanılmaması önemlidir. CBC ve CFB kipleri için aynı IV'nin tekrar kullanımı açık metnin ilk bloku hakkında ya da iki mesajın ortak ilk kısımları hakkında bilgi sızdırabilir. OFB ve CTR kiplerinde bir IV'yi yeniden kullanmak güvenliği tamamen yok eder. CBC kipinde IV ek olarak şifreleme anında tahmin edilememelidir, önceden yaygın olarak uygulanan bir sonraki mesajın IV'sini önceki mesajın son blokundaki şifreli metni olarak kullanmak güvenli değildir (bu yöntem SSL 2.0'da kullanılmıştır). Eğer bir saldırgan IV'nü (ya da önceki şifreli metin blokunu) sonraki açık metni seçmeden önce bilirse aynı anahtarla daha önce şifrelenmiş açık metinler hakkında tahmin yapabilir. (bu durum TLS CBC IV saldırısı olarak bilinir).[4]
Özel bir durum olarak, eğer açık metinler bir bloka sığacak kadar küçük ise, ECB, CBC, PCBC gibi bazı kiplerde aynı IV'yi tekrar kullanmak açık metinlerin aynı olup olmadığı bilgisini açığa çıkarır. Bu durum bir kişinin deşifreleme yapmadan aynı metnin şifrelenip şifrelenmediğini anlayabilmesine yol açar.
Doldurma[değiştir | kaynağı değiştir]
Bir blok şifre, blok uzunluğu denen sabit uzunluktaki parçalar üzerinde çalışır, ancak işlenecek mesaj uzunluğu herhangi bir uzunlukta olabilir. Bu yüzden ECB, CBC gibi kipler son blokun şifrelemeden önce tamamlanmasını gerektirir. Birçok doldurma şeması vardır. En basiti açık metni blok uzunluğunun katı yapacak şekilde sıfır dizisi eklemektir, ancak deşifrelemeden sonra açık metnin ilk uzunluğunun bilinebilmesi için dikkatli olmak gerekir; örneğin açık metin C biçiminde bir dizinin sadece sonunda sıfır bayt'ı içeriyorsa. Daha karmaşık bir yöntem mesaja tek adet bir bit'ini takiben yeterince sıfır bit'i ekleyerek bloku tamamlamayan DES yöntemidir; eğer orijinal mesajın uzunluğu blok uzunluğunun tam katıysa, bu durumda yeni bir tamamlama bloku eklenmiş olur. En karmaşık yöntemler fazladan kapalı metin üretimine neden olmayan ancak bunun karşılığında daha karmaşık olan CBC'ye has kapalı metin çalma tarzı şemalar veya artık blok sonlandırımı'dır. Schneier ve Ferguson iki basit yöntem önermiştir: değeri 128 (hex 80) olan bir bayt ve ardından son bloku dolduracak kadar sıfır bayt'ı ekleme veya son bloku değeri n olan n adet byte ile tamamlama.
CFB, OFB ve CTR kipleri açık metni şifrenin çıktısıyla XOR'lama işlemine tabi tuttukları için herhangi bir tamamlama gerektirmez. Bu kiplerde son açık metin parçası şifrenin çıktısının yeterli miktardaki kısmıyla XOR'lanarak açık metinle aynı uzunlukta kapalı metin oluşturur. Dizi Şifreleri'in bu özelliği onları şifreli metnin açık metinle aynı uzunlukta olması gerektiği veya verinin akan bir yapıda iletildiği ve tamamlamanın uygun olmaduğı uygulamalarda tercih sebebi yapar.
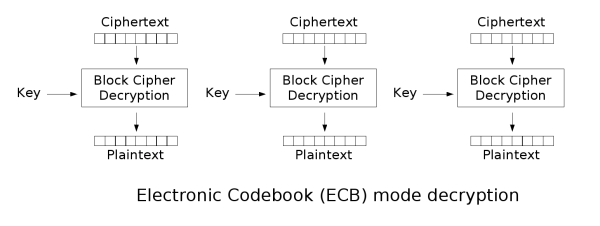
Elektronik kod defteri (ECB)[değiştir | kaynağı değiştir]
En basit şifreleme kipi elektronik kod defteri (ECB) kipidir. Mesaj parçalara ayrılır ve her parça ayrı ayrı şifrelenir.
Bu yöntemin dezavantajı aynı açık metinlerin şifrelendiğinde aynı kapalı metinlere dönüştürmesidir; bu yüzden mesajdaki örüntüleri belli eder. Başka bir deyişle mesaj gizliliği sağlanmayabilir ve kriprografik protokollerde kullanılması tavsiye olunmaz. ECB'nin açık metinlerdeki örüntüleri kapalı metinlere nasıl yansıttığının çarpıcı bir örneği aşağıda gösterilmiştir; soldaki resmin pikselleri ECB kipiyle şifrelendiğinde ortadaki resim meydana çıkmıştır, sağdaki resim ise ECB dışındaki bir kip ile yapılan şifreleme sonucunu yansıtmaktadır.

|

|

|
| Orijinal | ECB kipi ile şifrelenmiş | ECB dışında bir kip ile şifrelenmiş |
Sağdaki resim CBC, CTR gibi daha güvenli kipler kullanıldığında ortaya çıkan sonuçtur ve rassallıktan ayırt edilemez. Ancak resmin bu rassal görünüşü onun güvenli bir şekilde şifrelendiği anlamı taşımaz, çıktının rassal göründüğü birçok güvensiz şifreleme yöntemi vardır.
ECB kipi ayrıca doğruluk koruması bulunmayan prokollerde tekrar oynatma saldırılarına daha açıktır. Örneğin Phantasy Star Online: Blue Burst çevrimiçi oyunu Blowfish blok şifresini ECB kipinde kullanır. Daha büyük açıklara yol açan anahtar değişim protokolünün kırılmasından önce hile yapmak isteyenler Blowfish ile şifrelenmiş "monster killed" mesaj paketleri göndererek, oyunda haksız avantaj elde edebilmişlerdir.
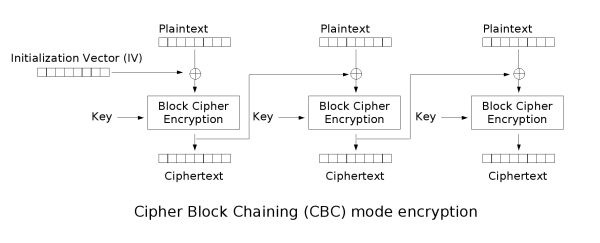
Şifre-bloku zincirleme (CBC)[değiştir | kaynağı değiştir]
Şifre-bloku zincirleme (CBC) kipi IBM tarafında 1976 yılında geliştirilmiştir.[5] CBC kipinde her açık metin bloku şifrelenmeden önce bir önceki kapalı metin bloku ile XORlanır. Bu sayede her kapalı metin bloku kendisinden önce gelen tüm açık metinlere bağımlı olmuş olur. Bir mesajın aynı anahtar altında tekrar şifrelendiğinin anlaşılamaması için ilk blokta ilklendirme vektörü (IV) kullanılmalıdır.
İlk blokun indeksine 1 dersek, CBC kipinin matematiksel ifadesi şu şekilde olur
CBC kipi ile şifrelenmiş metinin deşifreleme işlemi de şu şekilde yapılır
CBC kipi en yaygın olarak kullanılan kip olmuştur. Bu kipin en büyük dezavantajları blokların birbirine bağımlı olmalarından dolayı paralel olarak işlenememeleri ve tamamlama gerektirmesidir. Tamamlama sorununu çözmek için kapalı metin çalma yöntemi önerilmiştir.
Farklı bir IV ile deşifreleme yapmaya çalışmak ilk açık metin blokunun bozulmasına yol açarken diğer bloklar doğru şekilde deşifrelenecektir. Bunun sebebi bir açık metin blokunun kendisi ve önce gelen kapalı metin bloklarından çıkarılabilmesidir. Sonuç olarak deşifreleme işlemi paralelleştirilebilir. Bir kapalı metin bitindeki hata o bloktaki açık metni tamamen bozar ve sonraki bloktaki açık metinde de karşılık gelen bitlerde hataya yol açar, ancak sonraki bloklarda bir bozulma olmaz.
Yayılan şifre-bloku zincirleme (PCBC)[değiştir | kaynağı değiştir]
Yayılan şifre-bloku zincirleme kipi16 Temmuz 2012 tarihinde Wayback Machine sitesinde arşivlendi. ya da açık metin şifre-bloku zincirleme[6] kipi kapalı metindeki ufak değişikliklerin deşifreleme yaparken sonraki bloklara belirsiz bir şekilde yayılması için tasarlanmıştır.
Şifreleme ve deşifreleme şu şekilde yapılır:
PCBC Kerberos v4 ve WASTE'de kullanılmış ancak bunun dışında yaygın değildir. PCBC ile şifrelenmiş bir mesajda ardışık iki kapalı metin bloku yer değiştirirse bu sonraki blokların deşifrelenmesini etkilemez.[7] Bu sebeple PCBC Kerberos v5'te kullanılmamıştır.
Şifre Geri Bildirim(CFB)[değiştir | kaynağı değiştir]
Şifre geri bildirim kipi (CFB), CBC’nin bir benzeri olarak, bir blok şifreyi kendi kendine senkronize olan bir akış şifresi yapar. Bu operasyon oldukça benzerdir; özellikle, CFB şifre çözme, CBC şifrelenmesinin tersine gerçekleştirilmesiyle neredeyse aynıdır.


Kendinden senkronize şifre tanımından, eğer şifreli metnin bir parçası kaybolursa (iletim hatalarından kaynaklı olarak), bu durumda alıcı orijinal mesajın sadece bazı parçalarını kaybedecektir (bozuk içerik) ve bir miktar girdi verisi işlendikten sonra kalan blokların şifresini çözmeye devam eder. Bahsedilen bu CFB kullanımının kolay yolu, kendinden senkronize değildir. Eğer bir blok boyutu kadar şifreli metin kaybolduğunda ancak o zaman SFB senkron olacaktır, ama sadece tek bayt veya bit kaybetmek kalıcı olarak şifre çözümünü bozacaktır. Tek bit veya bayt kaybı olduğunda senkron hale getirebilmek için, bir seferde tek bir bayt veya bit şifrelenmedir. CFB, blok şifre için giriş olarak bir kaydırma yazmacı ile birleştirildiğinde bu şekilde kullanılabilir.
Kaybolan x bitlerinin herhangi biri için senkronize edecek kendinden senkronize olan bir akış şifresi oluşturmak amacıyla CFB kullanmak için, ilklendirme vektörü ile blok boyutunda bir kaydırma yazmacını oluşturarak başlayın. Bu blok şifre ile şifrelenir ve sonucun en yüksek x bitleri şifresiz metnin x bitleriyle xorlanır ve bu sayede şifreli metnin x bitlerini oluşturur. Çıktının bu x bitleri kaydırma yazmacına kaydırılır ve bu işlem (kaydırma yazmacını blok şifre ile şifreleme yaparak başlayan) şifresiz metnin sıradaki x bitleri için tekrar eder. Şifre çözme işlemi buna benzerdir, ilklendirme vektörü ile başlayın, sonucun yüksek bitlerini şifreli metnin x bitleri ile şifreleyip ve xorlayıp şifresiz metnin x bitleri oluşturulur, sonra şifreli metnin x bitlerini kaydırma yazmacına kaydırın ve yeniden şifreleyin. Bu şekilde devam etmek CFB-8 veya CFB-1(kaydırmanın büyüklüğüne bağlı) olarak biliniyor.
Notasyon olarak, Si kaydırma yazmacının durumu, a<<x a’nın x bit kaydırılması, head(a,x) a’nın x yüksek bitleri ve n ilklendirme vektörü (IV) bit sayısı:
Eğer şifreli metinden x bit kaybolursa, kaydırma yazmacı bir kez daha şifreleme sırasındaki duruma eşit oluncaya kadar şifre yanlış şifresiz metin üretir bu durumda şifre yeniden senkronize edilir. Bu, n/s blok boyutunda çıktının n blok boyutu ve s kaydırılan bit sayısı ile karışmasına neden olur.
CBC kipinde olduğu gibi, şifresiz metinde değişiklikler şifreli metinde sonsuza dek yayılır ve şifreleme paralelleştirilemez. CBC gibi, şifre çözme paralelleştirilebilir. Şifre çözme işlemi gerçekleştirilirken, şifreli metindeki bir bit değişikliği iki şifresiz metin bloklarını etkiler: karşılık gelen şifresiz metin bloğundaki bir bit değişiklik ve sonraki şifresiz metin bloğunun tamamındaki bozulma. Sonraki şifresiz metin blokları normal olarak çözülür.
CFB, CBC kipine göre akış şifreleme kipleri olan OFB ve CTR ile iki avantaj paylaşır: blok şifre sadece şifreleme yönünde kullanılır ve mesajın şifre bloğu katlarına doldurulması gerekmez (şifreli metnin çalınması, dolguyu gereksiz kılmak için kullanılabilir).
Çıktı geri bildirim(OFB)[değiştir | kaynağı değiştir]
Çıktı geri bildirim kipi bir blok şifreyi bir senkron akış şifre yapar. Anahtar akışı blokları oluşturur, bunlar daha sonra şifreli metin üretmek için şifresiz metin bloklarıyla XORlanır. Diğer akış şifrelerinde olduğu gibi, şifreli metinde bir bit döndürmek şifresiz metinde aynı konumda döndürülmüş bit üretir. Bu özellik, şifrelemeden önce uygulandığında bile hata düzeltme kodlarının normal çalışmasına izin verir.
XOR operasyonunun simetri özelliğinden dolayı şifreleme ve şifre çözme aynıdır:


Çıktı geri bildirim blok şifreleri operasyonları öncekilerin hepsine bağlıdır, bu yüzden paralel olarak çalıştırılamaz. Ancak, şifreli metin veya şifresiz metin sadece son XOR için kullanıldığından, blok şifreleme operasyonu işlemleri önceden gerçekleştirilebilir, son adımın şifreli veya şifresiz metin müsait olduğunda paralel çalıştırılabilmesine izin verilir.
CBC kipi ile girdi olarak sıfırlardan oluşan bir sabit dizi kullanarak OFB kipi anahtar akışı elde etmek mümkündür. Bu kullanışlı olabilir çünkü OFB kipi şifrelemesi için CBC kipi hızlı donanım implementasyonlarının kullanılmasına izin verir.
OFB kipini bir kısmi blokla geri bildirim olarak CFB kipi gibi kullanmak ortalama çevrim uzunluğunu 232 veya daha fazla bir faktör ile azaltır. Davies ve Parkin tarafından önerilen bir matematiksel model ve deneysel sonuçlarla doğrulanan yalnızca tam geri bildirim ile maksimuma yakın ortalama çevrim uzunluğunun elde edilebildiğini göstermiştir. Bu yüzden, kesik geri bildirim için destek OFB spesifikasyonundan kaldırılmıştır.
Sayaç (CTR)[değiştir | kaynağı değiştir]
Not: CTR kipi aynı zamanda tam sayı sayaç kipi (ICM) ve bölümlenmiş tam sayı sayaç kipi (SIC) olarak da bilinir.
OFB gibi, sayaç kipi bir blok şifreyi akış şifreye çevirir. Sonraki anahtar akış bloğunu bir “sayacın” ardışık değerlerini şifreleyerek oluşturur. Sayaç uzun bir süre tekrar etmeyeceği garanti olan bir dizi üreten herhangi bir fonksiyon olabilir, buna rağmen gerçek bir artış sayacı en basit ve en popüler olanıdır. Basit bir deterministik girdi fonksiyonu kullanımı önceden tartışmalıydı; eleştirmenler “kripto sistemi bilinen bir sistematik girdiye kasıtlı olarak maruz bırakmanın gereksiz bir risk temsil ettiğini” tartıştı. Ancak, günümüzde CTR kipi yaygın olarak kabul edilmektedir ve herhangi bir sorun girdisindeki sistemik yanlılığa bakılmaksızın güvenli olması beklenen blok şifresinin bir zayıflığı olarak kabul edilir. CBC ile, CTR kipi Niels Ferguson ve Bruce Schneier tarafından önerilen iki blok şifreleme kipinden biridir.
CTR kipi Whitfield Diffie ve Martin Hellman tarafından 1979 yılında tanıtıldı.
CTR kipi OFB kipi ile benzer karakteristiğe sahiptir, ama aynı zamanda şifre çözme sırasında rastgele erişim özelliğine izin verir. CTR kipi, blokların paralel olarak şifrelenebildiği çok işlemcili bir makinede çalışmak için uygundur. Ayrıca OFB’yi etkileyebilen kısa çevrim probleminden etkilenmez.
Eğer IV/tek-seferlik-şifre rastgele ise, daha sonra şifreleme için gerçek özgün sayaç bloğu üretmek üzere herhangi bir ters çevrilebilir işlem (ekleme, toplama veya XOR) kullanılarak sayaç ile birleştirilebilir. Rastgele olmayan tek-seferlik-anahtar durumunda (paket sayacı gibi), tek-seferlik-anahtar ve sayaç birleştirilmelidir (örneğin tek-seferlik-anahtarın 128 bit sayaç bloğunun üst 64 bitinde ve sayacın alt 64 bitinde depolanması). Basitçe tek-seferlik-anahtar ile sayacın tek bir değer olacak şekilde toplanması veya XORlanması çoğu durumda seçilen şifresiz metin saldırısı altında güvenliği bozar, çünkü saldırgan çarpışmaya sebep olmak için tüm IV-sayaç çiftlerini değiştirebilir. Saldırgan IV-sayaç çiftini ve şifresiz metni kontrol ettiğinde, şifreli metnin ve bilinen şifresiz metnin XORlanmasının ürettiği değer, aynı IV-sayaç çiftini paylaşan diğer bloğun şifresiz metniyle XORlandığında o bloğun şifresini çözer.
Bu şemadaki tek-seferlik-şifrenin diğer şemalardaki ilklendirme vektörüne (IV) eşdeğer olduğuna dikkat edin. Ancak, eğer uzaklık/konum bilgisi bozulmuşsa, bayt uzaklığına bağımlı olduğu için bu tür verilerin kısmi olarak kurtarılması imkânsız olacaktır.


Hata yayılımı[değiştir | kaynağı değiştir]
Mesaj doğrulama kodları ve kimlik doğrulamalı şifrelemenin yaygın kullanımından önce çalışma kipleri için "hata yayılımı" özellikleri bir seçim kriteri olarak tartışılmıştır. Örneğin bir blokta meydana gelen hatanın ECB kipinde bir bloku, CBC kipinde ise iki bloku etkilemesi gibi.
Bazıları bu esnekliğin rastgele oluşan hatalara karşı arzu edilen bir koruma sağladığını, bazıları ise bu hata kurtarmanın kötü niyetli kişilerin yapabileceği mesajla oynama türevi saldırıları mümkün kılacağını savunmuştur.
Bununla birlikte, gerekli bütünlük koruma önlemleri alınırsa, bu tarz hatalar tüm mesajın kabul edilmemesine yol açacaktır. Eğer rastgele hatalara karşı dayanıklılık isteniyorsa kapalı metin gönderilmeden önce hata düzeltme kodları kullanılmalıdır.
Kimlik doğrulamalı şifreleme[değiştir | kaynağı değiştir]
Gizlilik ve kimlik doğrulamayı tek bir kriptografik araçta birleştirmek için bir takım kipler tasarlanmıştır. Bu kiplerde bazıları XCBC,[8] IACBC, IAPM,[9] OCB, EAX, CWC, CCM ve GCM'dir. Kimlik doğrulamalı şifreleme kipleri tek geçiş ve çift geçişli kipler olarak sınıflandırılır. Maalesef kriptografi kullanıcıları için tek geçişli kiplerin çoğu (OCB kipi gibi) patent koruması altındadır.
Bunlara ek olarak AEAD (Authenticated-Encryption with Associated-Data) olarak adlandırılan bazı kipler şifrelenmemiş ilave verinin kimlik doğrulamasına olanak verir. Örnek olarak çift geçişli EAX kipi ve tek geçişli OCB kipi gösterilebilir.
Diğer kipler ve kriptografik primitifler[değiştir | kaynağı değiştir]
Blok şifreler için birçok kip önerilmiştir. Bazıları kabul görmüş, hatta standartlaşmış ve kullanımdadır. Bazıları da güvensiz bulunmuştur ve kullanılmaması gerekir. Gizlilik, kimlik doğrulamalı veya kimlik doğrulamalı şifreleme kategorilerine girmeyen Anahtar geribildirim kipi (KFM) ve AES-hash gibi örnekler de vardır.
NIST Modes Development4 Eylül 2017 tarihinde Wayback Machine sitesinde arşivlendi.).[10][11]'da önerilmiş blok şifre kiplerinin bir listesini tutar.
Disk şifreleme sıklıkla amaca özel tasarlanmış kipler kullanır. Bükülebilir dar-blok şifreleme kipleri (LRW, XEX ve XTS) ve geniş-blok şifreleme kipleri (CMC ve EME) disk sektörlerini güvenli bir şekilde şifrelemek için tasarlanmıştır. (Bkz. disk şifreleme teorisi)
Blok şifreler genellikle burada açıklanan blok şifre kiplerine benzer kiplerle diğer kriptografik protokollerde de kullanılır.
Bir blok şifreden kriptografik özet algoritması yapmak için çeşitli yöntemler vardır. Bunların açıklamaları için tek-yönlü sıkıştırma fonksiyonuna bakınız.
Blok şifrelerden Kriptografik olarak güvenli neredeyse-rassal sayı üreteçleri (CSPRNGs) yapılabilir.
Mesaj doğrulama kodları (MAC) genellikle blok şifrelerden üretilir. CBC-MAC, OMAC ve PMAC bunlara örnektir.
Kimlik doğrulamalı şifreleme bileşen olarak blok şifreleri kullanır. Bu kipler gizlilik ve kimlik doğrulamayı aynı anda sağlar. IAPM, CCM, CWC, EAX, GCM ve OCB gibi örnekleri mevcuttur.
Ayrıca bakınız[değiştir | kaynağı değiştir]
Kaynakça[değiştir | kaynağı değiştir]
- ^ a b c Alfred J. Menezes, Paul C. van Oorschot and Scott A. Vanstone (1996). Handbook of Applied Cryptography. CRC Press. ISBN 0-8493-8523-7. 7 Mart 2005 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Mayıs 2012.
- ^ "Block Cipher Modes". NIST Computer Security Resource Center. 27 Kasım 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 15 Temmuz 2012.
- ^ "FIPS 81: DES Modes of Operation". NIST Computer Security Resource Center. 3 Ocak 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Mayıs 2012.
- ^ B. Moeller (20 Mayıs 2004), Security of CBC Ciphersuites in SSL/TLS: Problems and Countermeasures, 30 Haziran 2012 tarihinde kaynağından arşivlendi, erişim tarihi: 15 Temmuz 2012
- ^ William F. Ehrsam, Carl H. W. Meyer, John L. Smith, Walter L. Tuchman, "Message verification and transmission error detection by block chaining", US Patent 4074066, 1976
- ^ Kaufman, C., Perlman, R., & Speciner, M (2002). Network Security. Upper Saddle River, NJ: Prentice Hall. Page 319 (2nd Ed.)
- ^ Kohl, J. "The Use of Encryption in Kerberos for Network Authentication", Proceedings, Crypto '89, 1989; published by Springer-Verlag; http://dsns.csie.nctu.edu.tw/research/crypto/HTML/PDF/C89/35.PDF 12 Haziran 2009 tarihinde Wayback Machine sitesinde arşivlendi.
- ^ Virgil D. Gligor, Pompiliu Donescu, "Fast Encryption and Authentication: XCBC Encryption and XECB Authentication Modes". Proc. Fast Software Encryption, 2001: 92-108.
- ^ Charanjit S. Jutla, "Encryption Modes with Almost Free Message Integrity", Proc. Eurocrypt 2001, LNCS 2045, May 2001.
- ^ "NIST: Recommendation for Block Cipher Modes of Operation" (PDF). 22 Temmuz 2017 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 22 Mayıs 2012.
- ^ "NIST: Modes Development". 4 Eylül 2017 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Mayıs 2012.
ISO/IEC 10116:2006 Information technology — Security techniques — Modes of operation for an n-bit block cipher17 Mart 2012 tarihinde Wayback Machine sitesinde arşivlendi.