Parabol

Parabol üzerinde alınan herhangi bir noktanın(P1, P2, P3) doğrultmana(L) ve odak noktasına(F) olan uzaklıkları eşittir.

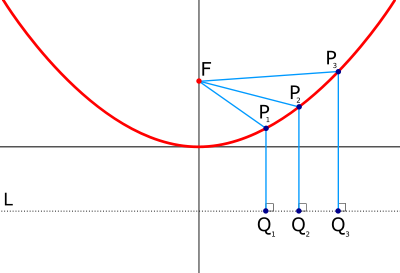
Parabol, bir düzlemde alınan sabit bir d doğrusu ile sabit bir F noktasından eşit uzaklıktaki noktaların geometrik yerleştirilmesidir. Cebirde ise y=ax²+bx+c şeklindeki ikinci derece fonksiyonları grafiği olarak bilinir.

Terimler

• Sabit F noktasına parabolün odağı, d doğrusuna da parabolün doğrultmanı denir.
• F noktasından geçip d doğrusuna dik olan doğruya parabol ekseni denir. Parabol, bu eksene göre simetrik iki koldan ibarettir. Parabol üzerindeki her noktanın odak noktasına olan uzaklığı, doğrultmana olan uzaklığına eşittir.
• Parabole ait herhangi iki noktayı birleştiren doğru parçasına kiriş denir.
• Odakta geçiğ parabol eksenine dik olan kirişin yarısına parametre denir ve p ile gösterilir.
• Parabolün ekseni kestiği noktaya tepe noktası adı verilir.

Denklemler

y=x² parabolü

Kartezyen koordinat sisteminde bir parabolün denklemi:

$y=ax^2+bx+c$ şeklindedir.

Burada a, parabolün yönünü gösterir. Eğer a>0 ise parabolün kolları yukarı doğrudur, eğer a<0 ise aşağı doğrudur. c değeri parabolün y ekseniyle kesiştiği yerdir.

Tepe noktası

Tepe noktasının koordinatları T(r,k) olarak gösterilir. Tepe noktasında fonksiyonun eğimi 0 olduğundan türev alınıp sıfıra eşitlenirse,

$r=\frac{-b} {2a}$,

$k=f(r)=\frac {4ac-b^2}{4a}$ bulunur. Ve denklem,

$y=f(x)=a(x-r)^2+k$ şeklinde yeniden yazılabilir. Aynı zamanda x=r doğrusu parabolün simetri ekseni olur.

Ayrıca bakınız

• Katener
• Elips
• Hiperbol
• Kubbe
• Parabolik yansıtıcı
• Parabolik kısmi diferansiyel denklem
• Parabloid
• 2. derece denklemler

Wikimedia Commons'ta

Parabol ile ilgili çoklu ortam belgeleri bulunmaktadır.