Fresnel denklemleri

Bu kısım ışığın değişmez düzlemsel arayüzeylerdeki yansımaları ve kırınımlarını tanımlayan Fresnel denklemleri hakkındadır.Işığın bir açıklık boyunca kırınımları için Fresnel kırınımlarına bakınız.İnce lensler ve ayna teknolojileri için Fresnel lens lerine bakınız.

Kısmi gönderim ve yüksek kırıcı dizin ortamından alçak dizin ortamına hareket eden dalganın yansıma genliği

Fresnel denklemleri (ya da Fresnel koşulları), Fransız fizikçi Augustin-Jean Fresnel İngilizce telaffuz: [frɛˈnɛl] tarafından ortaya çıkarılan,ışığın farklı opti ortamlardaki durumunu açıklayan bir dizi denklemdir. Işığın yansımasının denklemi Fresnel denklemi olarak bilinir.

Genel açıklama

Işık verilen bir kırınım dizini ortamından kırınım dizinin₂ olan ikinci bir ortama hareket ettiğinde,ışığın kırınımı veya kırınım olabilir. Fresnel denklemleri ışığın ne oranda yansıdığını ve ne oranda kırıldığını tanımlar. Onlar ayrıca yansıyan ışığın dalga evrelerini tanımlar. Denklemler arayüzün düz, düzlemsel, homojen ve ışığın düzlem dalgası olduğunu varsayar.

Tanımlar ve kuvvet denklemleri

Fresnel denklemlerinde ulanılan değişkenler.

Sağdaki diagramda, gelen ışığı demet IO kırınım dizinlerinin arasındaki arayüze çarpar. O noktasindan n₁ ve n₂ Işık demeti parçası OR ışını olarak yansıtılır ve OT olarak kırılır. Bu gelen ışığındaki açılar arayüzeylerin yüzey normallerini oluşturmak için yansır ve kırılırlar. yansıma _i, θ_r ve kırılma θ_t. Bu açılar arasındaki ilişki yansıma yasasıyla verilir ;

$\theta _{\mathrm {i} }=\theta _{\mathrm {r} }$

Ve Snell yasası;

${\frac {\sin \theta _{\mathrm {i} }}{\sin \theta _{\mathrm {t} }}}={\frac {n_{2}}{n_{1}}}$

Bu gelen ışığın fraksiyonu arayüzden yansıyan R (yansıyan) ve transmittans tarafından kırılan T.Ortamın manyetik olmadığı varsayılıyor. R ve T hesaplamaları özel ışık demetinin dalgalarının kutuplaşmasına bağlıdır.

1. Bu gelen ışık onun kırınım demetlerini,yansıyanı ve geleni içeren düzleme dik olan elektrik alanıyla kutuplaşır.örneğin; yukardaki diagramdaki düzlem. Işık kutuplaşmış denir .
2. Gelen ışık yukarıda tanımlanan düzleme paralel olan elektrik alanla kutuplaşır.Bu tür ışıklar p kutuplaşması olarak tanımlanır.

s-kutuplaşması yansıması

$R_{\mathrm {s} }=\left|{\frac {n_{1}\cos \theta _{\mathrm {i} }-n_{2}\cos \theta _{\mathrm {t} }}{n_{1}\cos \theta _{\mathrm {i} }+n_{2}\cos \theta _{\mathrm {t} }}}\right|^{2}=\left|{\frac {n_{1}\cos \theta _{\mathrm {i} }-n_{2}{\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\sin \theta _{\mathrm {i} }\right)^{2}}}}{n_{1}\cos \theta _{\mathrm {i} }+n_{2}{\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\sin \theta _{\mathrm {i} }\right)^{2}}}}}\right|^{2}$,

“p”-kutuplaşması olurken;

$R_{\mathrm {p} }=\left|{\frac {n_{1}\cos \theta _{\mathrm {t} }-n_{2}\cos \theta _{\mathrm {i} }}{n_{1}\cos \theta _{\mathrm {t} }+n_{2}\cos \theta _{\mathrm {i} }}}\right|^{2}=\left|{\frac {n_{1}{\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\sin \theta _{\mathrm {i} }\right)^{2}}}-n_{2}\cos \theta _{\mathrm {i} }}{n_{1}{\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\sin \theta _{\mathrm {i} }\right)^{2}}}+n_{2}\cos \theta _{\mathrm {i} }}}\right|^{2}$.

Her denklemin ikinci hali Snell yasası ve trigonometrik özelliklerin kullanılarak ve e θ_tyı eleyerek birinciden türetilebilir. Enerji korunumunun sonucu olarak transmistans katsayısı şöyle verilir ;

$T_{s}=1-R_{s}\,\!$

Ve

$T_{p}=1-R_{p}\,\!$

Bu ilişkiler yalnızca kuvvet katsayıları için geçerlidir,Genlik katsayıları yukarıda belirtildiği gibidir. Eğer gelen ışık kutuplaşmamışsa(p ve s kutuplaşmaları eşitse) yansıma katsaysı ;

$R={\frac {R_{s}+R_{p}}{2}}\,\!$

Yaygın camlar için yansıma katsayısı For θ_i = 0 yaklaşık 4%. Bir pencereden yansıma ön taraftan olduğu kadar arka taraftandır da ve bu tür ışıklar iki kenar arasında birçok kere ileri ve geri yapar.Bu durum için birleştirilmiş katsayısı 2R/(1 + R), karışma(dalga yayılması ) önemsenmediğinde (bakınız aşağı). Burada yapılan tarışma, vakum geçirgenliği elektromanyetik geçirgenliğin μ₀ materyalin manyetik olmadığı belirtilen iki ortamda eşit olduğu varsayılmasıdır. Bu yaklaşık olarak tüm yalıtkan maddeler için geçerlidir fakat bazı çeşitleri için geçerli değildir. Fresnel denklemleri daha karışıktır. Kutuplaşmanın önemsenemeyebileceği bilgisayar grafikleri gibi düşük hassasiyetteki uygulamalar için Schlick's tahminleri kullanılabilir.

Özel açılar

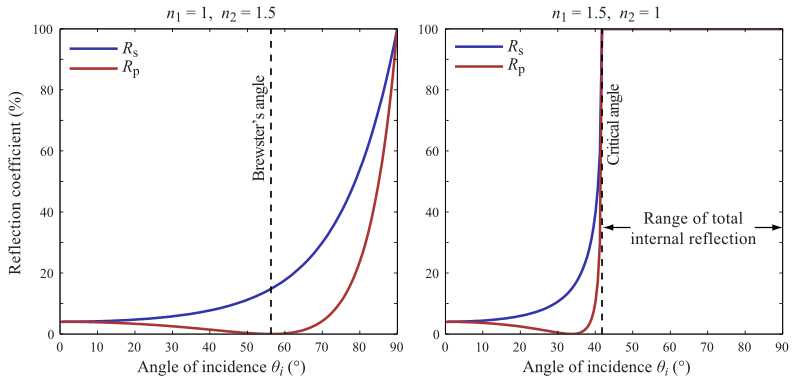
Şablon:Başlıca Belirli verilen bir açıda n₁ and n₂ R”değeri _p sıfıra gider ve p- gelen polarize ışın bütünüyle kırılır. Bu açı Brewster açısı olarak bilinir ve değeri hava ya da vakum ortamında olan bir cam için yaklaşık olarak olarak 56° dir.Bu cümle cam ve hava ortamında olan materyallerde olduğu gibi,yalnızca gelen kırınımlar iki materyal de gerçek sayı olduğu zaman doğrudur.Işığı absorbe eden metal ve yarı iletken maddeler için n karmaşık, ve ve R_p genellikle sıfıra gitmez. Yoğun ortamdan daha az yoğun bir ortama geçerken bir (örneğin, n₁ > n₂), yukarı geliş açısı, bütün ışığın yansıtıldığı ve R_s = R_p = 1 kritik açı olarak bilinir. Bu fenomen toplam iç yansıma olarak bilinir.Kritik açı hava ortamındaki camlar için yaklaşık olarak 41° dir.

Genlik denklemleri

Dalgaların karmaşık değerli elektrik alanına karşılık gelen katsayı denklemleri de Fresnel denklemleri olarak adlandırlır. Bunlar kullanılan biçimciliğe ve işaret anlaşmasına bağlı olan birçok farklı forma sahiptir. Katsayıların genliği daha düşük durumlar için genellikle r ve t ile temsil edilir. [[Dosya::Amptitude Ratios air to glass.JPG|küçükresim|sağ|havadan cama genlik oranı]]

camdan havaya genlik oranı

Burada kullanılan kurallar

Bu işlemde r katsayısı yansıyan dalganın karmaşık sayı olan elektrik alan genliğinin gelen dalganın elektrik alan genliğine oranıdır. t katsayısı iletilen dalganın elektrik alan genliğinin gelen dalganın elektrik alan genliğine oranıdır. Işık yukarıda tanımladığı gibi s ve p kutuplaşmalarına ayrılır.(sağdaki figurde, s kutuplaşması "$\bot$" ile belirtilmiştir ve p "$\parallel$"ile belirtilmiştir.)

s-kutuplaşması için, bir pozitif r ya da t gelen ya da yansıyan ve iletilen dalganın elektrik alanlarının paralel olduğu anlamına gelirken ,negatif r ya da t paralel olmadığı anlamına gelir. F p-kutuplaşması için, bir pozitif r ve t dalganın manyetik alanlarının paralel olduğu anlamına gelirken,negatif paralel olmadıpı anlamına gelir. Ayrıca İki ortamin manyetik geçirgenliğinin µ boş alanın geçirgenliğine µ₀ eşit oduğunu varsayar.

Formüller

Yukarıdaki kuralları kullanarak,

$r_{s}={\frac {n_{1}\cos \theta _{\text{i}}-n_{2}\cos \theta _{\text{t}}}{n_{1}\cos \theta _{\text{i}}+n_{2}\cos \theta _{\text{t}}}}$

$t_{s}={\frac {2n_{1}\cos \theta _{\text{i}}}{n_{1}\cos \theta _{\text{i}}+n_{2}\cos \theta _{\text{t}}}}$

$r_{p}={\frac {n_{2}\cos \theta _{\text{i}}-n_{1}\cos \theta _{\text{t}}}{n_{1}\cos \theta _{\text{t}}+n_{2}\cos \theta _{\text{i}}}}$

$t_{p}={\frac {2n_{1}\cos \theta _{\text{i}}}{n_{1}\cos \theta _{\text{t}}+n_{2}\cos \theta _{\text{i}}}}$

Şunun farkına varın;$t_{s}=1+r_{s}$ but $t_{p}\neq 1+r_{p}$.

Yansıma genliği yansıma R ile ilişkilidir çünkü gelen ve yansıyan dalgalar aynı ortamda yayılır ve yüzeyin normaliyle aynı açıyı yaparlar.:$R=\left|r\right|^{2}$.

iletme T genellikle |t|²’ye eşit değildir çünkü ışık iki ortamda farklı yön ve farklı hızlarda hareket eder.iletme t ile ilişkilidir.

$T={\frac {n_{2}\cos \theta _{\text{t}}}{n_{1}\cos \theta _{\text{i}}}}\left|t\right|^{2}$.

n faktörü ₂/n₁ yoğunlukların ( parlaklıkla çok yakından ilişkili ) oranından kaynaklanır.cos θ_t/cos θ_i faktörü ışın demetlerininmalanındaki değişimi temsil eder. Kırınım dizinin oranları açısından;

$\rho =n_{2}/n_{1}$,

Ve ışık demetinin ara yüzünde olan m oranından,

$T=\rho mt^{2}$.

Çok katlı yüzeyler

Işık bir ya da daha fazla paralel yüzeyler arasında yansıma yaptığı zaman ,çokkatlı ışık demetleri genellikle birbiriyle karışır ( dalga yayılımı) ve net iletim ve bu ışığın dalga boyuna bağlı olan yansıma genliği ile sonuçlanır.ancak girişim yalnızca yüzeyler ışığın sırdan beyaz ışık için birkaç mikrometre olan ve bir lazer için çok daha fazla büyük oalbilen tutunum uzunluğundan küçük ya da kıyaslanabilir olduğunda görülebilir.

Yansımalar arasındaki girişimin bir örneği sabun kabarcığında görlen renkli pırıltılar ya da sudaki ince yağ zarlarıdır. Fabry–Pérot interferometre lerini içeren uygulamalar; yansıma olmayan kat ve optic filtreler. Bu etkilerin bir sayısal analizi Fresnel denklemlerine dayanır fakat girişim hesaplarına ek hesaplamalarda yapılır.

Transfer matrix methodu ya da tekrarlamalı Rouard methodu çoklu yüzey problemlerini çözmek için kullanılabilir.

Ayrıca bakınız

• Index-materyalleri eşleştirme
• Fresnel eşkenar dörtgen, dairesel kutuplaşmış ışık üretmek için Fresnel araçları [1]28 Ağustos 2017 tarihinde Wayback Machine sitesinde arşivlendi.
• yansıtıcı yansıma
• Schlick yaklaşımı
• Snell penceresi
• X-ray yansıtırlık

Kaynakça

• Hecht, Eugene (1987). Optics (2.2yayıncı=Addison Wesley bas.). ISBN 0-201-11609-X. 
• Hecht, Eugene (2002). Optics (4.4yayıncı=Addison Wesley bas.). ISBN 0-321-18878-0. 

Destek bilgi

• The Cambridge Handbook of Physics Formulas, G. Woan, Cambridge University Press, 2010, ISBN 978-0-521-57507-2.
• Introduction to Electrodynamics (3rd Edition), D.J. Griffiths, Pearson Education, Dorling Kindersley, 2007, ISBN 81-7758-293-3
• Light and Matter: Electromagnetism, Optics, Spectroscopy and Lasers, Y.B. Band, John Wiley & Sons, 2010, ISBN 978-0-471-89931-0
• The Light Fantastic – Introduction to Classic and Quantum Optics, I.R. Kenyon, Oxford University Press, 2008, ISBN 978-0-19-856646-5
• Encyclopaedia of Physics (2nd Edition), R.G. Lerner, G.L. Trigg, VHC publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1, ISBN (VHC Inc.) 0-89573-752-3
• McGraw Hill Encyclopaedia of Physics (2nd Edition), C.B. Parker, 1994, ISBN 0-07-051400-3

Dış bağlantılar

• Fresnel Equations27 Nisan 2006 tarihinde Wayback Machine sitesinde arşivlendi. – Wolfram
• FreeSnell18 Aralık 2008 tarihinde Wayback Machine sitesinde arşivlendi. – Free software computes the optical properties of multilayer materials
• Thinfilm16 Ocak 2010 tarihinde Wayback Machine sitesinde arşivlendi. – Web interface for calculating optical properties of thin films and multilayer materials. (Reflection & transmission coefficients, ellipsometric parameters Psi & Delta)
• Simple web interface for calculating single-interface reflection and refraction angles and strengths.16 Ocak 2010 tarihinde Wayback Machine sitesinde arşivlendi.
• Reflection and transmittance for two dielectrics – Mathematica interactive webpage that shows the relations between index of refraction and reflection.
• A self-contained first-principles derivation 13 Mayıs 2014 tarihinde Wayback Machine sitesinde arşivlendi. of the transmission and reflection probabilities from a multilayer with complex indices of refraction.