Fibonacci dizisi

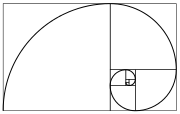
Fibonacci dizisi, her sayının kendinden önceki ile toplanması sonucu oluşan bir sayı dizisidir. Ayrıca ardışık her iki sayının bölümü altın orana yakın bir değer vermektedir değer ne kadar büyük olursa altın orana o kadar yakın olur örneğin:55:34=1,617... 1, 2, 3, 5, 8, 13, 21, 34, 55, 89... şeklinde devam eden bu dizide sayılar birbirleriyle oranlandığında altın oran ortaya çıkar, yani bir sayı kendisinden önceki sayıya bölündüğünde altın orana gittikçe yaklaşan bir dizi elde edilir. Bu durumda genel olarak n'inci Fibonacci sayısı F(n) şu şekilde ifade edilir:
Bu da bir Fibonacci dizisidir: 4, 4, 8, 12, 20, 32, 52, … Çünkü Fibonacci dizisi herhangi iki sayıdan başlayabilir.
Fibonacci sayı dizisindeki sayıların birbirleriyle oranı olan ve altın oran denilen 1,618 sayısı ise doğada, sanatta ve hayatın her alanında görülen ve estetik ile bağdaştırılan bir sayıdır.
Ayrıca Pascal Üçgeninde de fibonacci sayı dizisi bulunmaktadır.
Ayrıca bakınız[değiştir | kaynağı değiştir]
| Matematik ile ilgili bu madde taslak seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |

