Kardiyoit
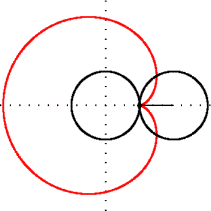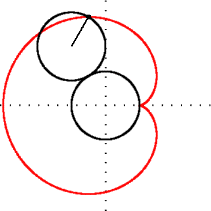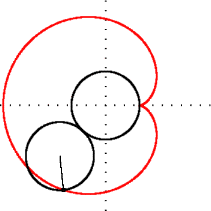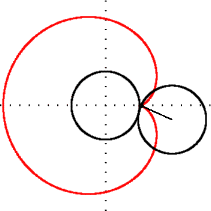
Matematikte kardiyoit veya yürek eğrisi, sabit bir çember üzerinde yuvarlanmakta olan aynı yarıçaplı ikinci bir çember üzerindeki herhangi bir noktanın izlediği eğridir. İsmi Yunanca kardia (kalp) ve eidos (şekil) kelimelerinin birleşiminden oluşur. Kalp (♥) şeklini anımsattığı için bu ismi almıştır. Kardiyoit ismini ilk kullanan, 18. yüzyıl İtalyan matematikçisi Johann Castillon olmuştur.[1]
Yarıçapı a olan iki çemberin oluşturduğu kardiyoit, Kartezyen koordinat sisteminde şu denklemle ifade edilir:
Aynı eğri, 0 < t < 2π için şu parametrik denklemlerle de ifade edilebilir:
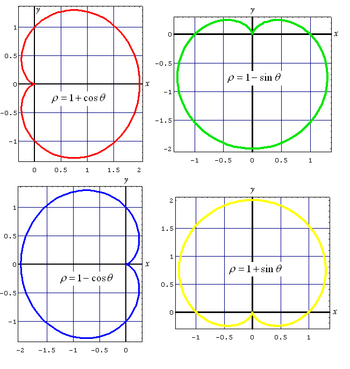
Kutupsal koordinat sisteminde ise kardiyoidin ifadesi şöyledir:
Trigonometrik fonksiyonların bazı özellikleri sayesinde, bu denklemdeki kosinüs ifadesi sinüs ile değiştirilebilir, eksi yerine de artı yazılabilir. Ortaya çıkan şekiller, aynı kardiyoidin orijin çevresinde döndürülmüş kopyaları olacaktır:
Kardiyoit, limaçon eğrisinin özel bir örneğidir.
Alan ve çevre[değiştir | kaynağı değiştir]
a yarıçaplı iki çemberin oluşturduğu kardiyoitin çevre uzunluğu ve alanı, kutupsal koordinatlar yardımıyla kolayca hesaplanabilir:
Kaynakça[değiştir | kaynağı değiştir]
- ^ "Cardioid" (İngilizce). 27 Mayıs 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 26 Temmuz 2007.
Dış bağlantılar[değiştir | kaynağı değiştir]
- MacTutor Matematik Tarihi Arşivi'nden Kardiyoit 11 Haziran 2007 tarihinde Wayback Machine sitesinde arşivlendi. sayfası (İngilizce)
- MathWorld'den Kardiyoit 15 Temmuz 2007 tarihinde Wayback Machine sitesinde arşivlendi. sayfası (İngilizce)
- yürek egrisi (Cardioid) yürek eğrisi java appleti